YBTOJ 4.5LCA问题
A.树上距离
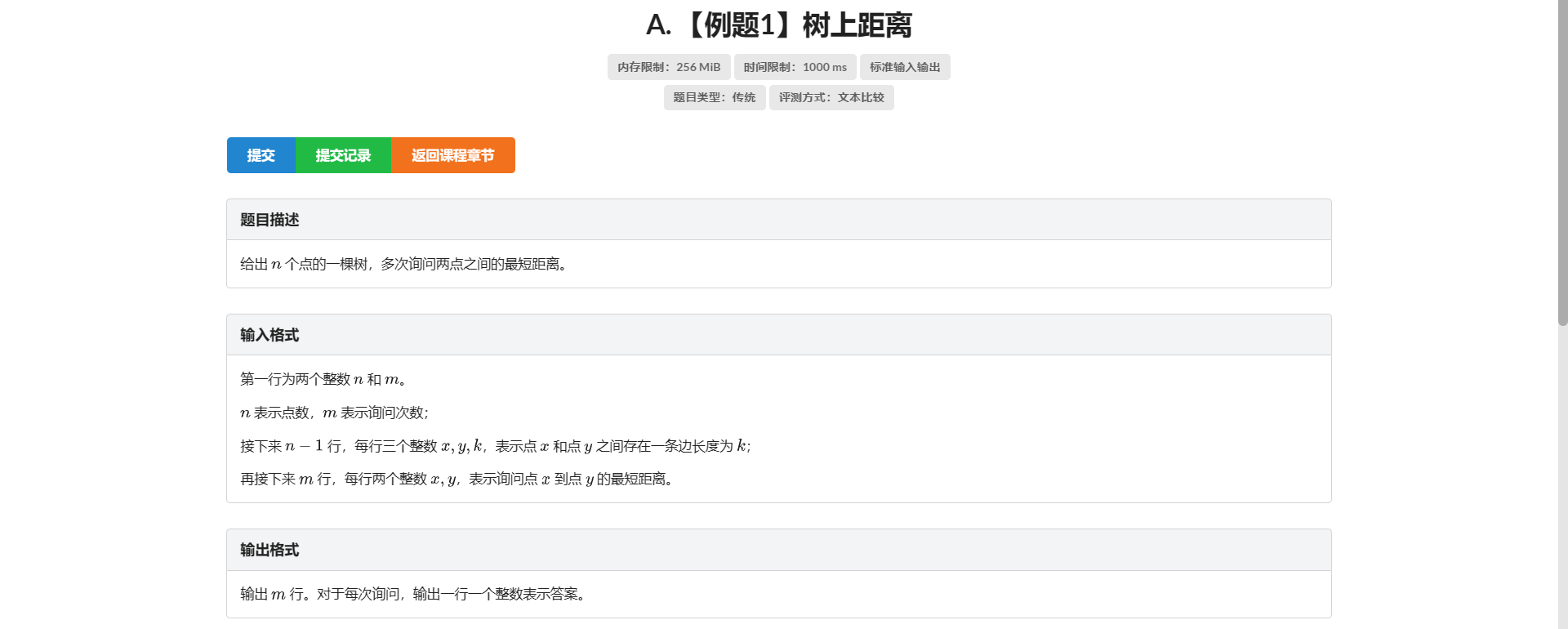
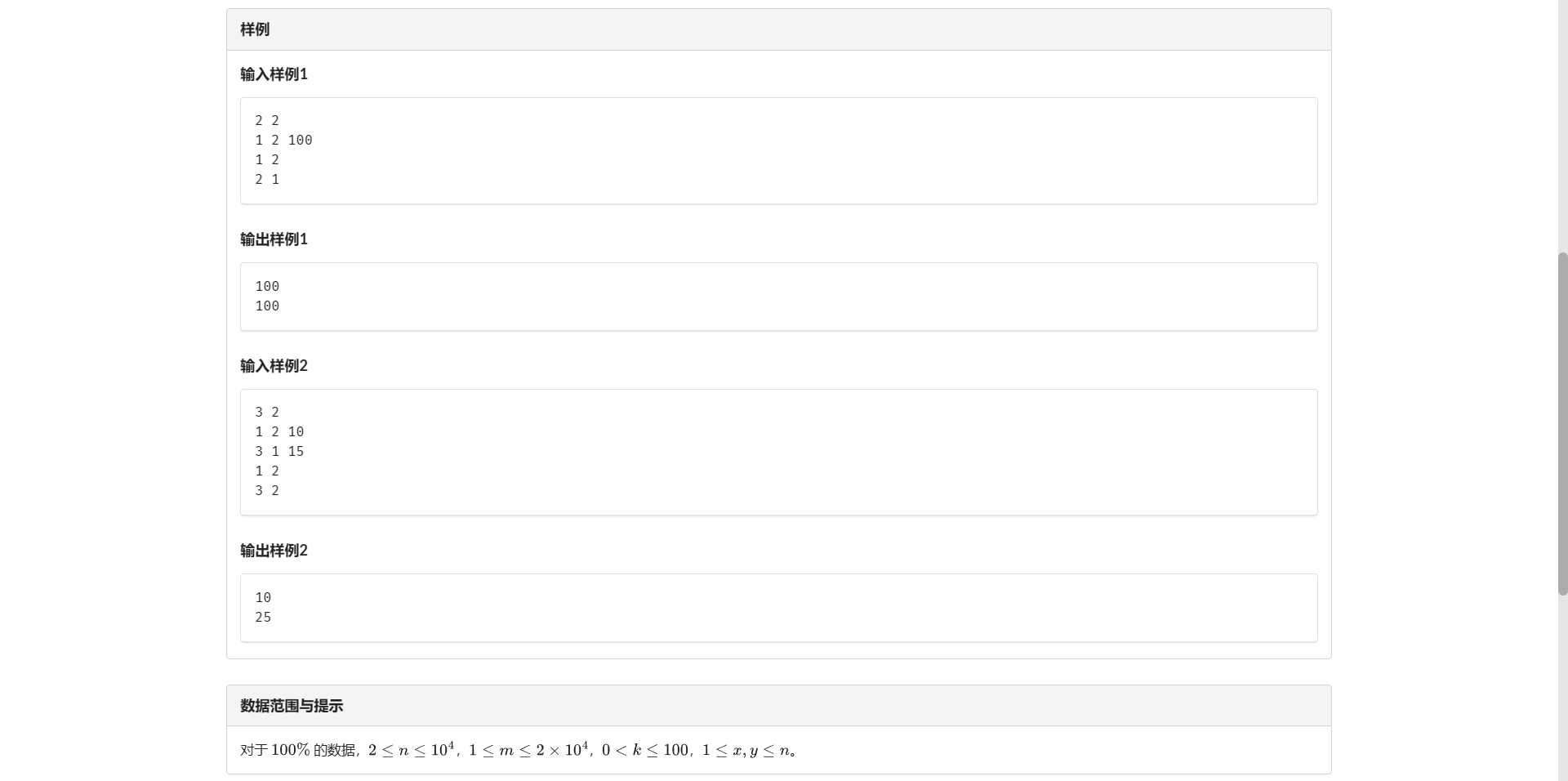
板子 详见P3379 最近公共祖先模板
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
int head[N], nxt[N], to[N], len[N], cnt;
int dep[N], fa[N][21], dis[N];
int n, m;
inline void cmb(int x, int y, int z) {
to[++cnt] = y;
len[cnt] = z;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x, int f) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (f == y)
continue;
dep[y] = dep[x] + 1;
dis[y] = dis[x] + len[i];
fa[y][0] = x;
dfs(y, x);
}
}
inline int lca(int x, int y) {
if (dep[x] < dep[y])
swap(x, y);
for (int j = 20; j >= 0; --j) {
if (dep[fa[x][j]] >= dep[y])
x = fa[x][j];
}
if (x == y)
return x;
for (int j = 20; j >= 0; --j) {
if (fa[x][j] != fa[y][j])
x = fa[x][j], y = fa[y][j];
}
return fa[x][0];
}
int main() {
// freopen("1.txt", "r", stdin);
scanf("%d%d", &n, &m);
for (int i = 1; i < n; ++i) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
cmb(x, y, z);
cmb(y, x, z);
}
dfs(1, 0);
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i <= n; ++i) fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
while (m--) {
int x, y;
scanf("%d%d", &x, &y);
int ans = dis[x] + dis[y] - (dis[lca(x, y)] << 1);
printf("%d\n", ans);
}
return 0;
}
B.货车运输
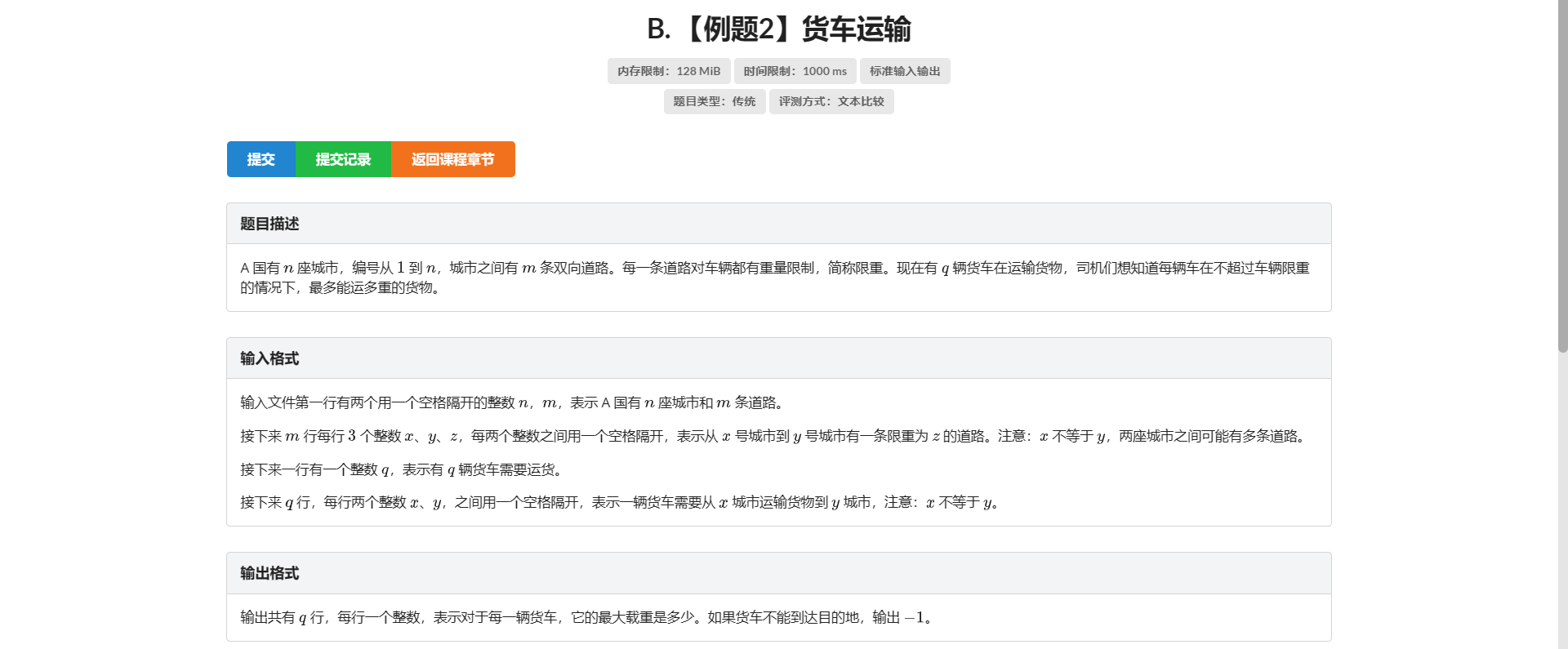
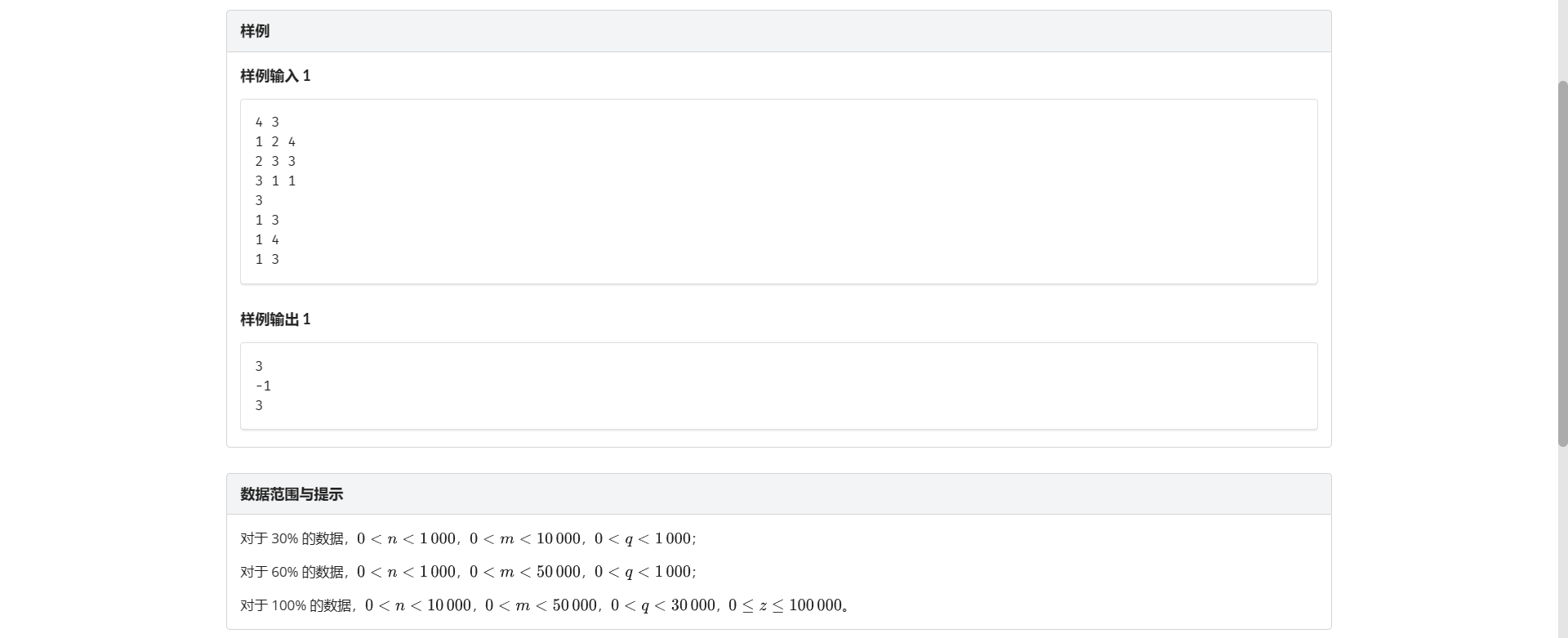
首先思考 我们是要让货车从这个点走到另一个点的路径上最小边的边权最大
进而想到 对于每个询问 我们二分一个答案 把小于这个答案的边都删掉
然后判能不能走到
复杂度 \(O(n * q * log z)\)
但是这样有过不去的风险 所以考虑有没有别的做法
发现瓶颈在于每次询问都要查询连通性
那我们可不可以先让其联通呢
并且我们要让这个连通图上的边边权尽可能地大
想到最大生成树
那么每次查询的时候直接查询两点树上路径上边权最大的边即可 倍增维护
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
int head[N], nxt[N], to[N], len[N], cnt;
int dep[N], fa[N][21], maxdis[N][21];
int fath[N];
int n, m, q, rt;
struct node {
int u, v, w;
friend bool operator<(node x, node y) { return x.w > y.w; }
} r[N];
inline void cmb(int x, int y, int z) {
to[++cnt] = y;
len[cnt] = z;
nxt[cnt] = head[x];
head[x] = cnt;
}
int find(int x) {
return (fath[x] == x)? x: fath[x] = find(fath[x]);
}
inline void kruskal(void) {
sort(r + 1, r + 1 + m);
for (int i = 1; i <= n; ++i) fath[i] = i;
for (int i = 1; i <= m; ++i) {
int u = r[i].u, v = r[i].v, w = r[i].w;
int fu = find(u), fv = find(v);
if (fu == fv) continue;
fath[fu] = fv;
cmb(u, v, w);
cmb(v, u, w);
rt = u;
}
}
void dfs(int x, int f) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == f) continue;
dep[y] = dep[x] + 1;
fa[y][0] = x;
maxdis[y][0] = len[i];
dfs(y, x);
// cout<<x<<" "<<y<<endl;
}
}
inline int lca(int x, int y) {
int res = 0x7fffffff;
if (dep[x] < dep[y]) swap(x, y);
for (int i = 20; i >= 0; --i) {
if( dep[fa[x][i]] >= dep[y]) {
res = min(res, maxdis[x][i]);
x = fa[x][i];
}
}
if (x == y)
return res;
for (int i = 20; i >= 0; --i) {
if (fa[x][i] != fa[y][i]) {
res = min(res, maxdis[x][i]);
res = min(res, maxdis[y][i]);
x = fa[x][i];
y = fa[y][i];
}
}
res = min(res, maxdis[x][0]);
res = min(res, maxdis[y][0]);
return res;
}
int main() {
// freopen("1.txt", "r", stdin);
memset(maxdis, 0x3f, sizeof(maxdis));
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) scanf("%d%d%d", &r[i].u, &r[i].v, &r[i].w);
kruskal();
// cout<<rt<<endl;
dfs(rt, 0);
// for (int i = 1; i <= n; ++i) cout<<maxdis[i][0]<< " ";
// cout<<endl;
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i <= n; ++i) {
fa[i][j] = fa[fa[i][j - 1]][j - 1];
maxdis[i][j] = min(maxdis[i][j - 1], maxdis[fa[i][j - 1]][j - 1]);
// cout<<i<<" "<<j<<" "<<maxdis[i][j]<<endl;
}
}
scanf("%d", &q);
for (int i = 1; i <= q; ++i) {
int x, y;
scanf("%d%d", &x, &y);
int fx = find(x), fy = find(y);
if (fx != fy) {
printf("-1\n");
continue;
}
printf("%d\n",lca(x, y));
}
return 0;
}
C.运输计划
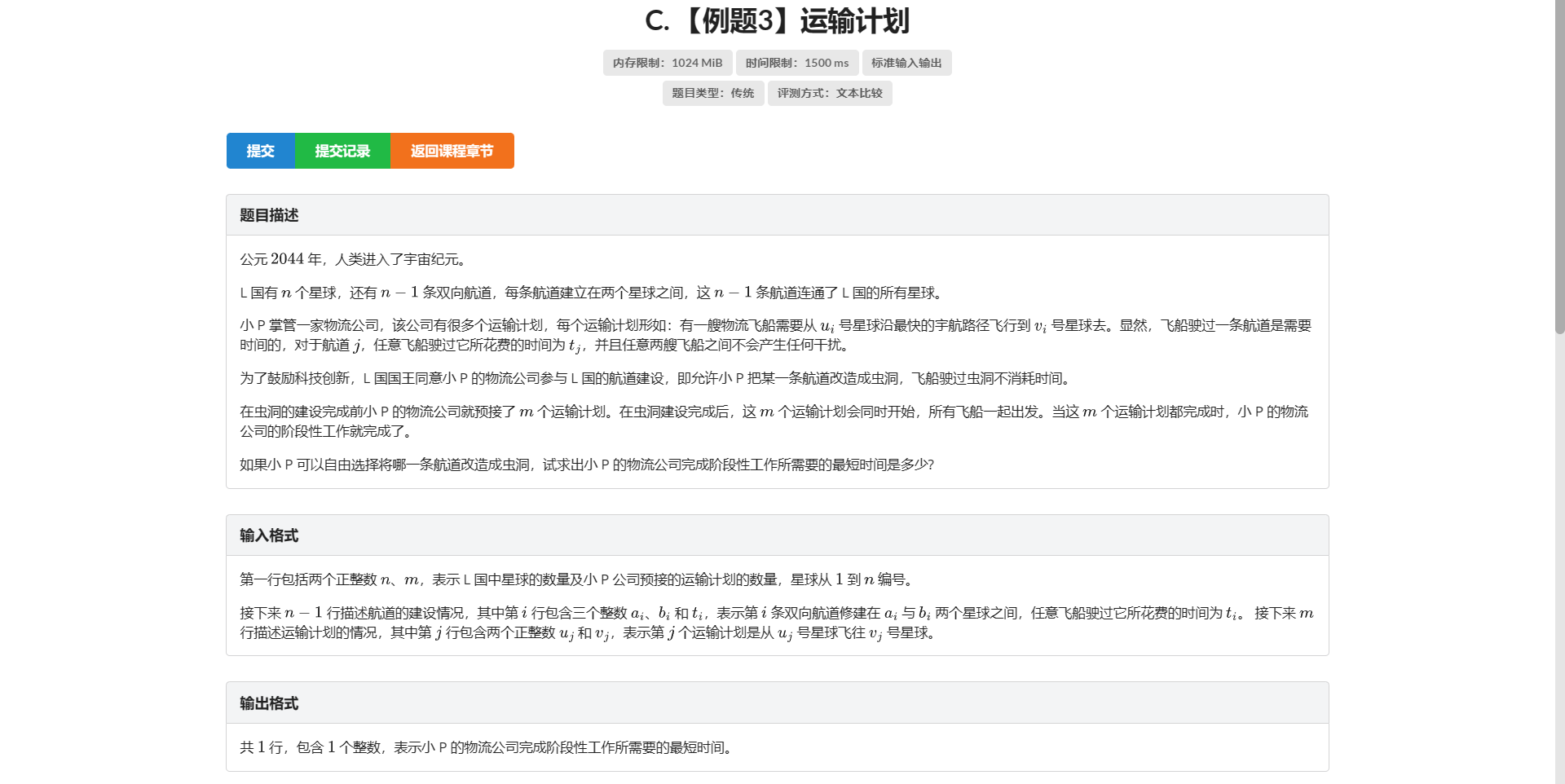
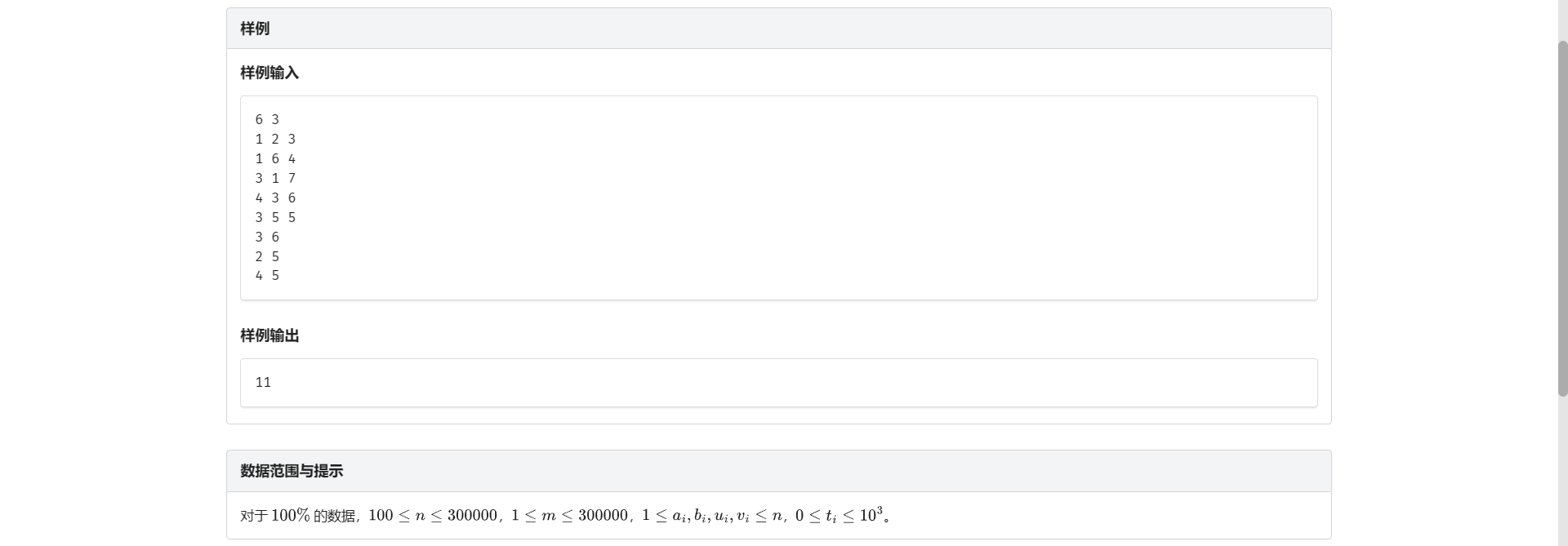
为啥 LCA 的例题都这么难啊
很容易想到的一个暴力:枚举改成虫洞的边 然后计算当前运输完成时间
看了看这题哈人的数据范围 还是算了吧
要求完成工作的最小时间 想到二分答案
然后对于那条最长的路径 就把路径上与当前答案长度之差大于这条边的边考虑删除
但是同时尽量要让它被第二条 第三条长路所经过
然后我就不会了
实际上这个思路离正解不远
因为我们二分答案 所有长度大于 \(mid\) 的路径中都要有一条边被经过
所以我们就找是否有一条最大的边 它被这些所有路径所经过 并且最长路径减去它是否小于 \(mid\)
判一条边被经过多少次使用树上差分实现
但是注意 边是没有编号的 但是在一颗树上 儿子只有一条边连向父亲
所以我们可以用儿子节点的编号代替那条边的编号
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 0721;
int fa[N][21], dep[N], dis[N], fadis[N];
int head[N], nxt[N << 1], to[N << 1], len[N << 1], cnt;
int v[N];
int n, m;
int sum;
struct node {
int x, y, lca, dis;
friend bool operator<(node a, node b) { return a.dis > b.dis; }
} qu[N];
inline void cmb(int x, int y, int z) {
to[++cnt] = y;
len[cnt] = z;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x, int f) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == f) continue;
dis[y] = dis[x] + len[i];
dep[y] = dep[x] + 1;
fadis[y] = len[i];
fa[y][0] = x;
dfs(y, x);
}
}
void init(void) {
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i <= n; ++i) fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
}
int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
for (int j = 20; j >= 0; --j) {
if (dep[fa[x][j]] >= dep[y])
x = fa[x][j];
}
if (x == y) return x;
for (int j = 20; j >= 0; --j) {
if (fa[x][j] != fa[y][j]) {
x = fa[x][j];
y = fa[y][j];
}
}
return fa[x][0];
}
void dfs_(int x, int f) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (f == y) continue;
dfs_(y, x);
v[x] += v[y];
}
}
bool check(int x) {
for (int i = 1; i <= n; ++i) v[i] = 0;
int nn = 0;
for (int i = 1; i <= m; ++i) {
if (qu[i].dis <= x) break;
++v[qu[i].x], ++v[qu[i].y];
--v[qu[i].lca], --v[qu[i].lca];
++nn;
}
dfs_(1, 0);
int maxn = 0;
for (int i = 1; i <= n; ++i) {
if (v[i] == nn)
maxn = max(maxn, fadis[i]);
}
return qu[1].dis - maxn <= x;
}
int main() {
// freopen("1.txt", "r", stdin);
scanf("%d%d", &n, &m);
for (int i = 1; i <= n - 1; ++i) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
cmb(x, y, z);
cmb(y, x, z);
}
dfs(1, 0);
init();
for (int i = 1; i <= m; ++i) {
scanf("%d%d", &qu[i].x, &qu[i].y);
qu[i].lca = lca(qu[i].x, qu[i].y);
qu[i].dis = dis[qu[i].x] - dis[qu[i].lca] + dis[qu[i].y] - dis[qu[i].lca];
sum = max(qu[i].dis, sum);
}
sort(qu + 1, qu + 1 + m);
int l = 0, r = sum;
int mid, ans;
while (l <= r) {
mid = (l + r) >> 1;
if (check(mid)) {
ans = mid;
r = mid - 1;
}
else
l = mid + 1;
}
printf("%d",ans);
return 0;
}
D.次小生成树
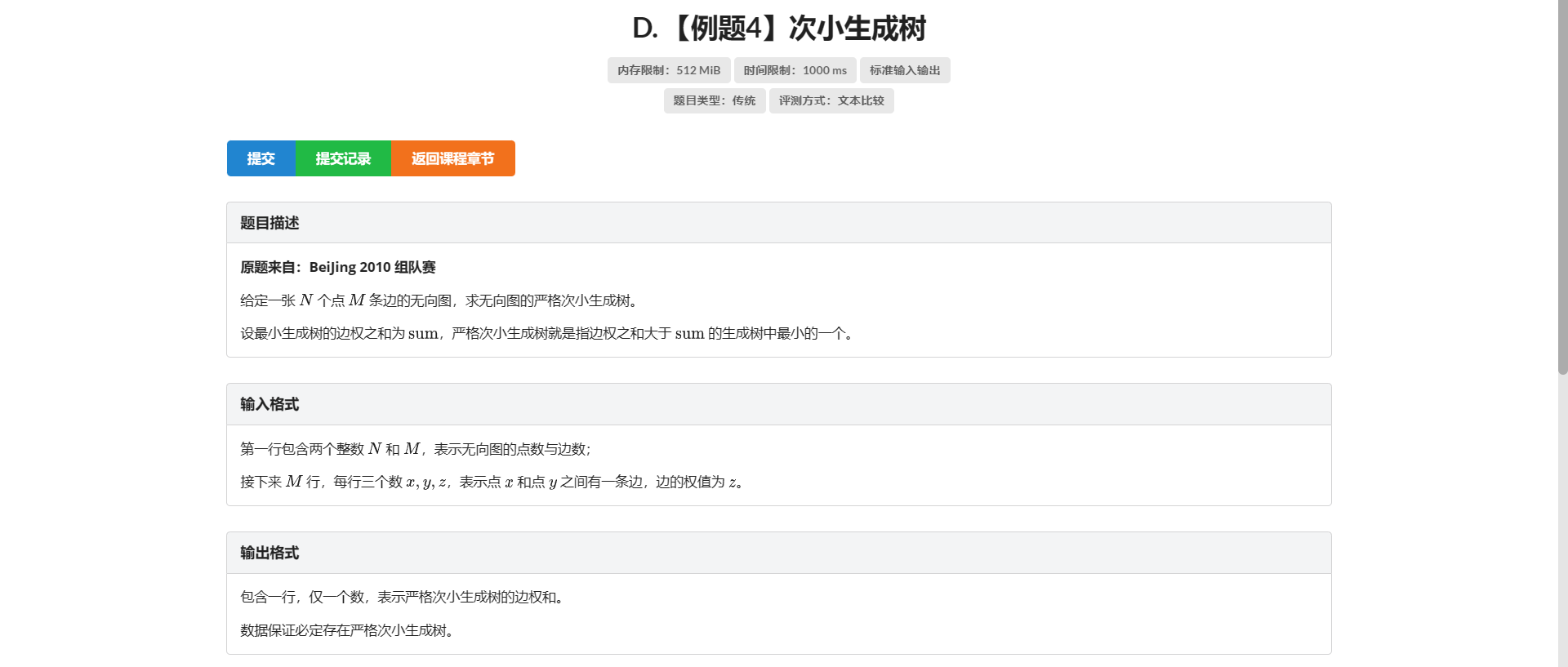
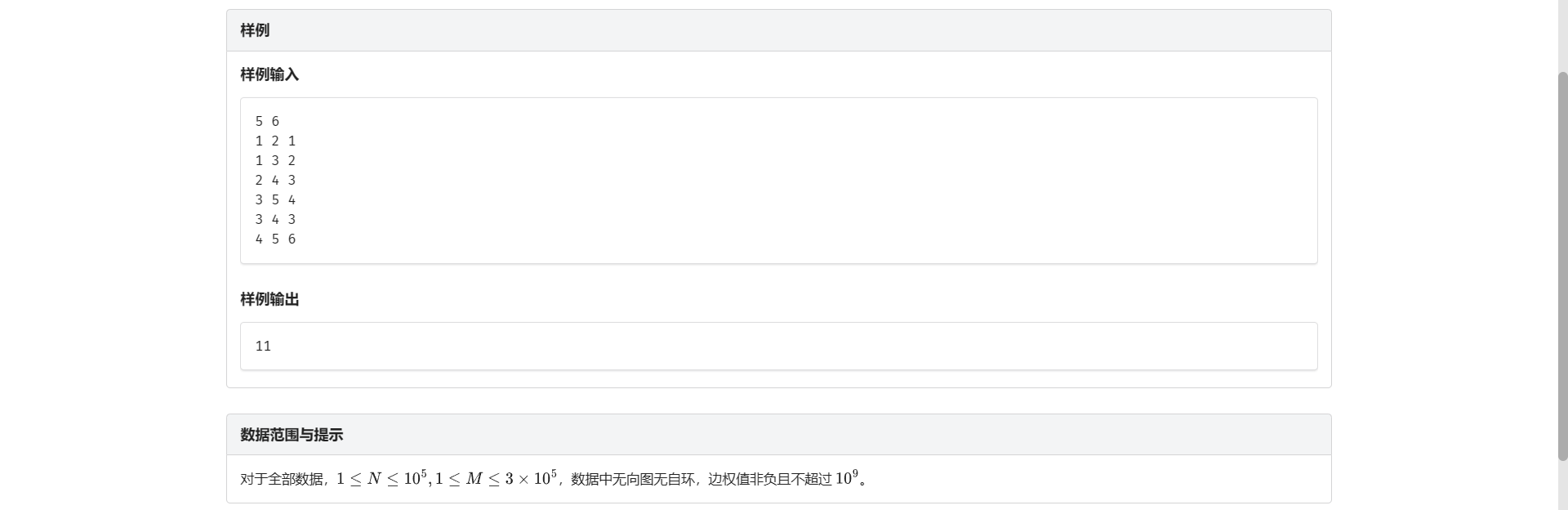
所以为啥 LCA 的例题都这么难啊!!!
目前码过最长的一道题 虽然一堆复制粘贴
非常谔谔的一道题
真是啥思路都没有啊
一个很直接的思路就是跑最小生成树特意保留一些很小的边不用
但是这样会对各集合的连通性产生影响 不太可行
那我们换个角度考虑 假如我们已经有一个连通图 然后把一些边拿掉 再把一些边加上 那么维护这个连通性是不是能稍微方便点
进一步想到 如果我这个连通图是一颗树 是不是连通性就更好维护了
我们是否可以考虑先弄一棵树出来
但是随便弄棵树显然有点亏 能不能让这个树具有一定的特点
连猜带蒙猜想要不弄个最小生成树
进一步考虑 这个树上的所有边肯定不能同时出现在次小生成树中
那我们就需要拿掉一些边 再加上一些边
又因为要求次小的 所以只拿掉一条边 再加上一条边显然是最好的
考虑枚举拿掉的边 再从原来落选的边集里选一条最小的并且能将两个连通块重新连起来的边
但这样做还是有些麻烦 因为能连接两个连通块的边实在是太多了 并且不好找
那我们能不能考虑反过来做 即枚举落选的边 把这条边加上然后断掉一条边
然后我们发现 如果把它加上 那么会它和它两端点的树上路径会构成一个环 拿走这个环上的任意一条边都是可以的
显然我们要让这个差值最小 所以要拿走最大的那条边
就可以用倍增 \(LCA\) 来维护了
但是注意 要考虑最小生成树不唯一的情况 有可能最大的那条边和你要放的边边权一样
那它就不是一个次小生成树了
所以还要维护一下两点间距离的次大值
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define int long long
using namespace std;
const int N = 3e5 + 0721;
const int inf = -0x7ffffffffffffff;
struct node {
int u, v, len, id;
friend bool operator<(node a, node b) { return a.len < b.len; }
} edge[N];
struct nod {
int maxn, maxx;
};
int fa[N][21], maxn[N][21], maax[N][21], dep[N];
int head[N << 1], nxt[N << 1], to[N << 1], len[N << 1], cnt;
int faa[N];
int a[10];
bool vis[N];
ll ans;
ll anss[N];
int n, m;
inline void cmb(int x, int y, int z) {
to[++cnt] = y;
len[cnt] = z;
nxt[cnt] = head[x];
head[x] = cnt;
}
int find(int x) { return (faa[x] == x) ? x : faa[x] = find(faa[x]); }
void kruskal(void) {
for (int i = 1; i <= n; ++i) faa[i] = i;
sort(edge + 1, edge + 1 + m);
for (int i = 1; i <= m; ++i) {
int fu = find(edge[i].u), fv = find(edge[i].v);
if (fu == fv)
continue;
faa[fu] = fv;
vis[edge[i].id] = 1;
ans += edge[i].len;
cmb(edge[i].u, edge[i].v, edge[i].len);
cmb(edge[i].v, edge[i].u, edge[i].len);
}
}
void dfs(int x, int faf) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == faf)
continue;
dep[y] = dep[x] + 1;
fa[y][0] = x;
maxn[y][0] = len[i];
dfs(y, x);
}
}
void init(void) {
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i <= n; ++i) {
fa[i][j] = fa[fa[i][j - 1]][j - 1];
a[1] = maxn[i][j - 1], a[2] = maax[i][j - 1];
a[3] = maxn[fa[i][j - 1]][j - 1], a[4] = maax[fa[i][j - 1]][j - 1];
int maxval = 0;
for (int i = 1; i <= 4; ++i) {
if (maxval < a[i])
maxval = a[i];
}
maxn[i][j] = maxval;
int maaxvl = 0;
for (int i = 1; i <= 4; ++i) {
if (a[i] != maxval && maaxvl < a[i])
maaxvl = a[i];
}
maax[i][j] = maaxvl;
}
}
}
nod lca(int x, int y) {
// cout<<x<<" "<<y<<endl;
int ret = inf, retx = inf;
if (dep[x] < dep[y])
swap(x, y);
for (int j = 20; j >= 0; --j) {
if (dep[fa[x][j]] >= dep[y]) {
a[1] = maxn[x][j], a[2] = maax[x][j];
a[3] = ret, a[4] = retx;
int maxval = 0;
for (int i = 1; i <= 4; ++i) {
if (maxval < a[i])
maxval = a[i];
}
ret = maxval;
int maaxvl = 0;
for (int i = 1; i <= 4; ++i) {
if (a[i] != maxval && maaxvl < a[i])
maaxvl = a[i];
}
retx = maaxvl;
x = fa[x][j];
// cout<<ret<<" "<<retx<<endl<<endl;
}
}
if (x == y)
return { ret, retx };
for (int j = 20; j >= 0; --j) {
if (fa[x][j] != fa[y][j]) {
a[1] = maxn[x][j], a[2] = maax[x][j];
a[3] = ret, a[4] = retx;
a[6] = maxn[y][j], a[5] = maax[y][j];
int maxval = 0;
for (int i = 1; i <= 6; ++i) {
if (maxval < a[i])
maxval = a[i];
}
ret = maxval;
int maaxvl = 0;
for (int i = 1; i <= 6; ++i) {
if (a[i] != maxval && maaxvl < a[i])
maaxvl = a[i];
}
retx = maaxvl;
x = fa[x][j];
y = fa[y][j];
}
}
a[1] = maxn[x][0], a[2] = maax[x][0];
a[3] = ret, a[4] = retx;
a[6] = maxn[y][0], a[5] = maax[y][0];
int maxval = 0;
for (int i = 1; i <= 6; ++i) {
if (maxval < a[i])
maxval = a[i];
}
ret = maxval;
int maaxvl = 0;
for (int i = 1; i <= 6; ++i) {
if (a[i] != maxval && maaxvl < a[i])
maaxvl = a[i];
}
retx = maaxvl;
return { ret, retx };
}
signed main() {
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= m; ++i) {
scanf("%lld%lld%lld", &edge[i].u, &edge[i].v, &edge[i].len);
edge[i].id = i;
}
memset(maxn, -0x3f, sizeof(maxn));
memset(maax, -0x3f, sizeof(maax));
kruskal();
dfs(1, 0);
init();
// for (int i = 1; i <= m; ++i)cout<<vis[i]<<" ";
for (int i = 1; i <= m; ++i) {
if (vis[edge[i].id])
continue;
nod now = lca(edge[i].u, edge[i].v);
// cout<<edge[i].u<<" "<< edge[i].v << " "<<now.maxn<<" "<<now.maxx<<endl;
if (ans - now.maxn + edge[i].len != ans)
anss[i] = ans - now.maxn + edge[i].len;
else
anss[i] = ans - now.maxx + edge[i].len;
}
ll ansss = 0x7ffffffffffffff;
for (int i = 1; i <= m; ++i) {
if (anss[i] != 0)
ansss = min(ansss, anss[i]);
}
printf("%lld", ansss);
return 0;
}
E.祖孙询问
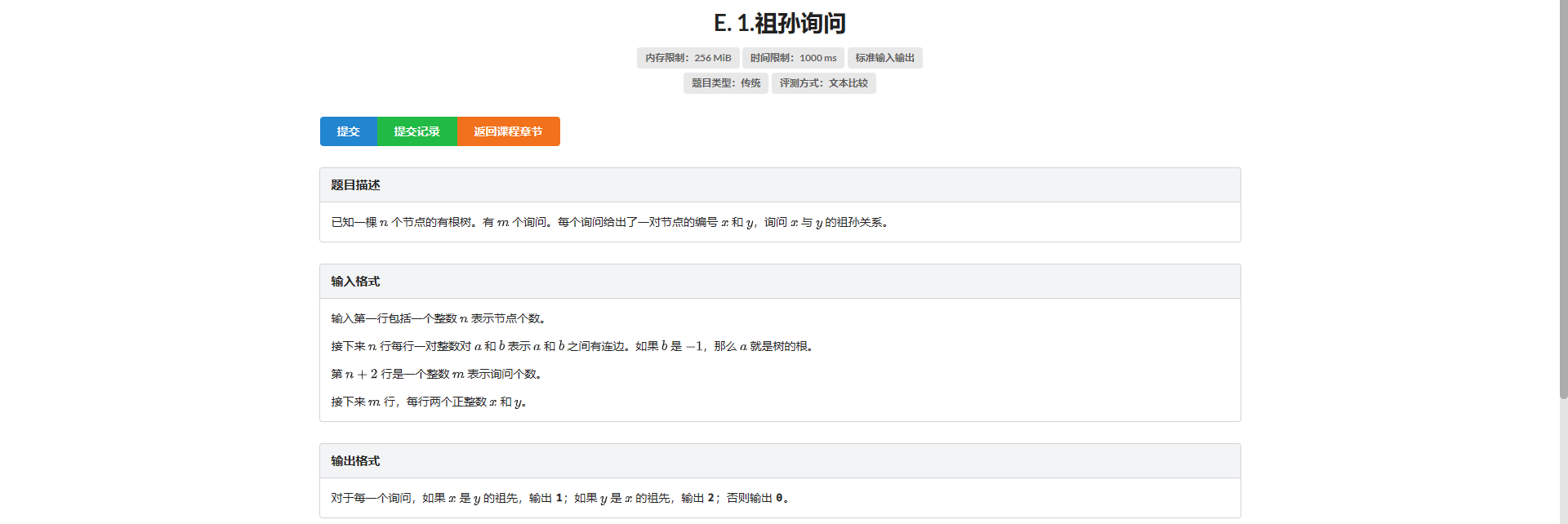
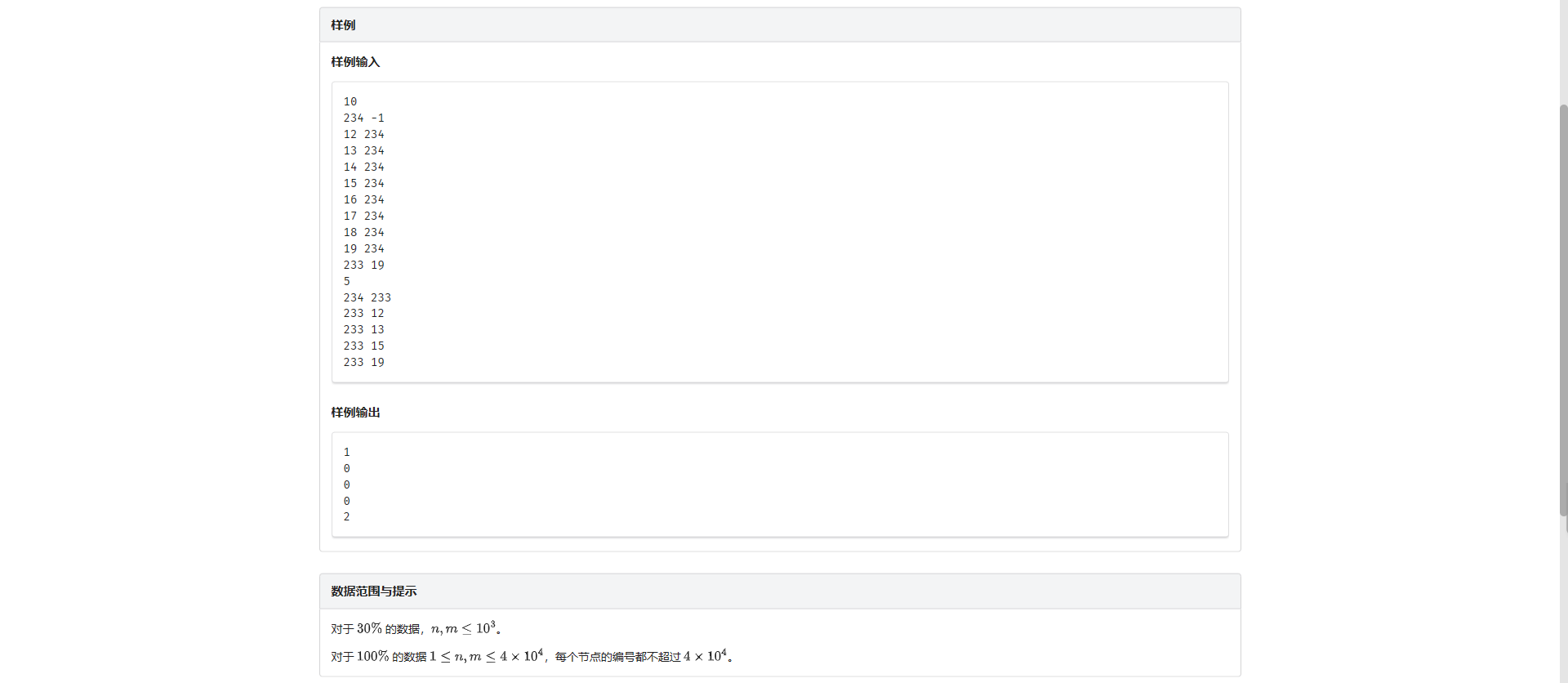
。。。没啥好说的
直接判断 LCA 是不是自己即可
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
int to[N], head[N], nxt[N], cnt;
int fa[N][21], dep[N];
bool vis[N];
int n, m, rt, maxn;
inline void cmb(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x, int f) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == f) continue;
dep[y] = dep[x] + 1;
fa[y][0] = x;
dfs(y, x);
}
}
void init(void) {
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i <= maxn; ++i) {
if (vis[i])
fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
}
}
int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
// cout<<x<<" "<<y<<" "<<dep[x]<<" "<<dep[y]<<endl;
for (int j = 20; j >= 0; --j) {
if (dep[fa[x][j]] >= dep[y]) {
// cout<<fa[x][j]<<" "<<dep[fa[x][j]]<<" "<<dep[y]<<endl;
x = fa[x][j];
}
}
if (x == y) return x;
for (int j = 20; j >= 0; --j) {
if (fa[x][j] != fa[y][j]) {
x = fa[x][j];
y = fa[y][j];
}
}
return fa[x][0];
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int x, y;
scanf("%d%d", &x, &y);
vis[x] = 1, vis[y] = 1;
maxn = max(maxn, max(x, y));
if (y == -1) rt = x;
else {
cmb(x, y);
cmb(y, x);
}
// cout<<maxn<<endl;
}
dep[rt] = 1;
dfs(rt, -1);
init();
scanf("%d", &m);
for (int i = 1; i <= m; ++i) {
int x, y;
scanf("%d%d", &x, &y);
int zx = lca(x, y);
// cout<<zx<<" ";
if (x == zx) printf("1\n");
else if (y == zx) printf("2\n");
else printf("0\n");
}
return 0;
}
F.删边操作
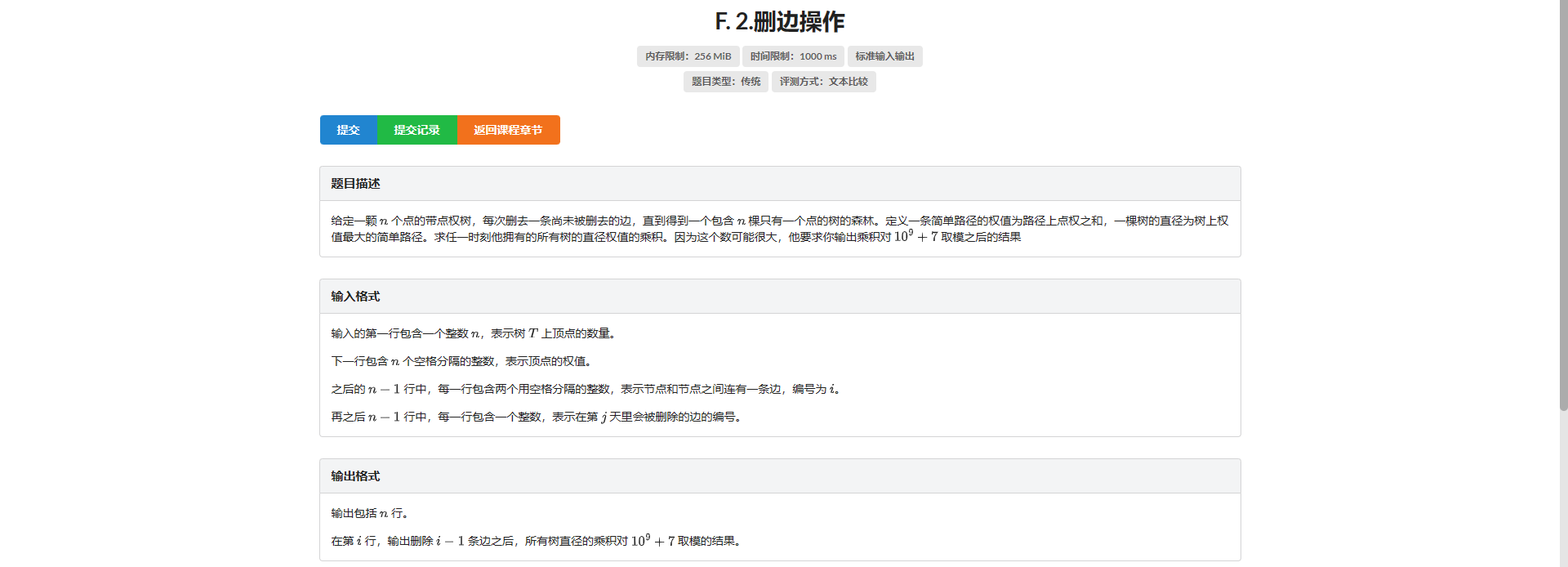
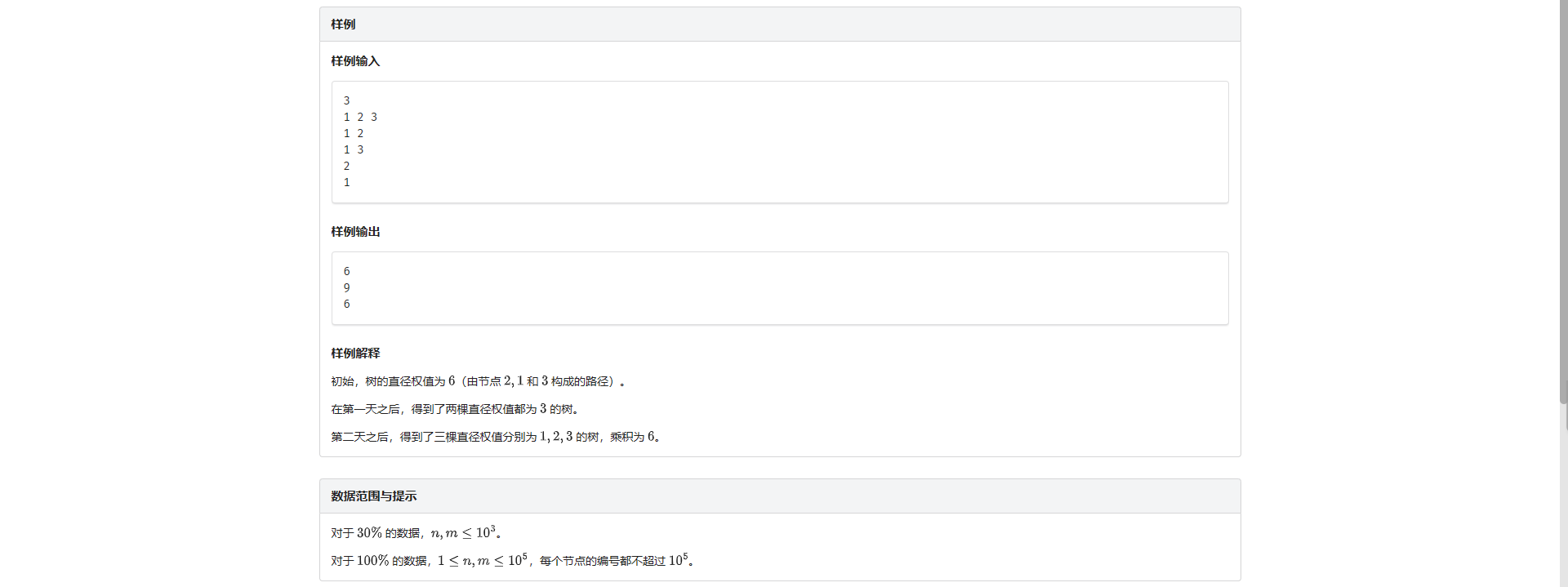
一道比较巧妙的题 这里说一下我的思路
发现删边操作不太好处理 考虑倒着做改成加边 然后发现非常好处理
因为对于新树的直径 假设连上的那条边的两个端点是 \(u\) \(v\)
那么新树的直径一定是 \(u\) 所在树的直径 / \(v\) 所在树的直径 / \(u\) 在它所在树里能走到的最远路径 + \(v\) 在它所在树里能走到的最远路径 这三个取 \(\max\)
那么对于前两个 显然非常好维护 主要在于最后一个东西
这时想到直径的性质 一个点出发能走到的最远路径一定是要么到直径的这一端点 要么是到直径的另一端点
所以实际上我们就要查找这个点到它所在树上直径的两个端点的距离 然后取 \(\max\) 即可
然后还有一个问题 就是我们是不断在连边的 所以维护的 \(fa\) 可能会产生变化
那么这个东西可以考虑拿 LCT 碾过去
开玩笑的 LCT 狗都不写
我们发现这个东西是只有连边操作的 或者说我们这个东西是断边生成的 也就是说对于一块联通块而言 它的形态和原树中这一块的形态一定是一致的
说人话就是任意两点之间的路径和它俩在原树上的路径是一样的 还是不明白可以自己画个图看下(
所以我们直接维护原树的信息 查询拿这个查即可
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 1e5 + 0721;
const int mod = 1e9 + 7;
ll sum[N];
int v[N], dep[N], del[N];
int fa[21][N];
int head[N], nxt[N << 1], to[N << 1], cnt;
ll ans[N];
int n;
struct D {
int s, t;
ll len;
} d[N];
struct edge {
int u, v, id;
} e[N];
struct DSU {
int fa[N];
void init() {
for (int i = 1; i <= n; ++i) fa[i] = i;
}
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
} dsu;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' | cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
ll ksm(ll x, int y) {
ll ret = 1;
while (y) {
if (y & 1) ret = ret * x % mod;
x = x * x % mod;
y >>= 1;
}
return ret;
}
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x, int f) {
dep[x] = dep[f] + 1;
sum[x] = sum[f] + v[x];
fa[0][x] = f;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == f) continue;
dfs(y, x);
}
}
void init() {
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i <= n; ++i) fa[j][i] = fa[j - 1][fa[j - 1][i]];
}
}
int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
for (int j = 20; j >= 0; --j) {
if (dep[fa[j][x]] >= dep[y]) x = fa[j][x];
}
if (x == y) return x;
for (int j = 20; j >= 0; --j) {
if (fa[j][x] != fa[j][y]) {
x = fa[j][x];
y = fa[j][y];
}
}
return fa[0][x];
}
ll dis(int x, int y) {
int lc = lca(x, y);
return sum[x] + sum[y] - sum[lc] - sum[fa[0][lc]];
}
void main() {
n = read();
dsu.init();
for (int i = 1; i <= n; ++i) v[i] = read();
for (int i = 1; i < n; ++i) {
e[i].u = read(), e[i].v = read();
e[i].id = i;
add_edge(e[i].u, e[i].v);
add_edge(e[i].v, e[i].u);
}
for (int i = 1; i < n; ++i) del[i] = read();
dfs(1, 0);
init();
ll tmp = 1;
for (int i = 1; i <= n; ++i) {
tmp = tmp * v[i] % mod;
d[i].s = d[i].t = i;
d[i].len = v[i];
}
ans[n] = tmp;
for (int i = n - 1; i >= 1; --i) {
int id = del[i];
int u = e[id].u, v = e[id].v;
int fu = dsu.find(u), fv = dsu.find(v);
tmp = tmp * ksm(d[fu].len, mod - 2) % mod * ksm(d[fv].len, mod - 2) % mod;
int su = d[fu].s, tu = d[fu].t;
int sv = d[fv].s, tv = d[fv].t;
int du, dv;
ll lu, lv;
ll dis1, dis2;
dis1 = dis(u, su), dis2 = dis(u, tu);
if (dis1 > dis2) du = su;
else du = tu;
lu = max(dis1, dis2);
dis1 = dis(v, sv), dis2 = dis(v, tv);
if (dis1 > dis2) dv = sv;
else dv = tv;
lv = max(dis1, dis2);
dsu.fa[fv] = fu;
if (d[fv].len > d[fu].len) {
d[fu].len = d[fv].len;
d[fu].s = d[fv].s;
d[fu].t = d[fv].t;
}
if (lu + lv > d[fu].len) {
d[fu].len = lu + lv;
d[fu].s = du;
d[fu].t = dv;
}
tmp = tmp * d[fu].len % mod;
ans[i] = tmp;
}
for (int i = 1; i <= n; ++i) printf("%lld\n", ans[i]);
}
}
int main() {
steven24::main();
return 0;
}
/*
3
1 2 3
1 2
1 3
2
1
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号