YBTOJ 4.4线段树
A.求区间和
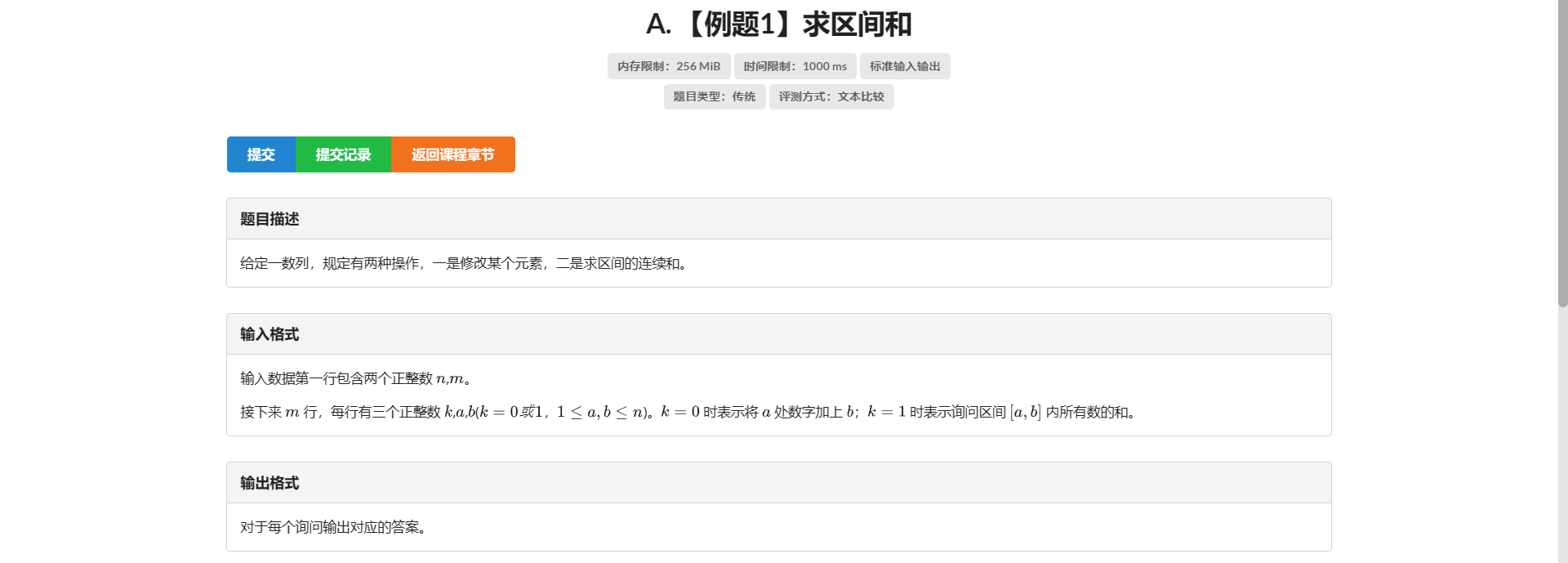
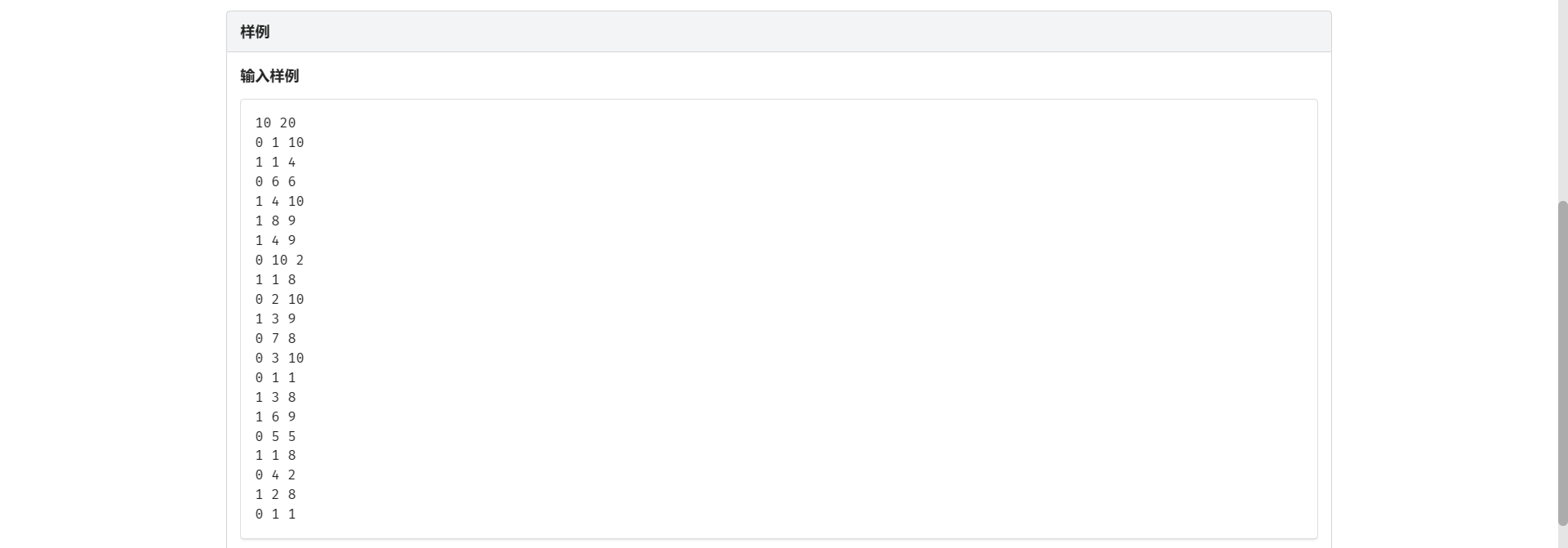
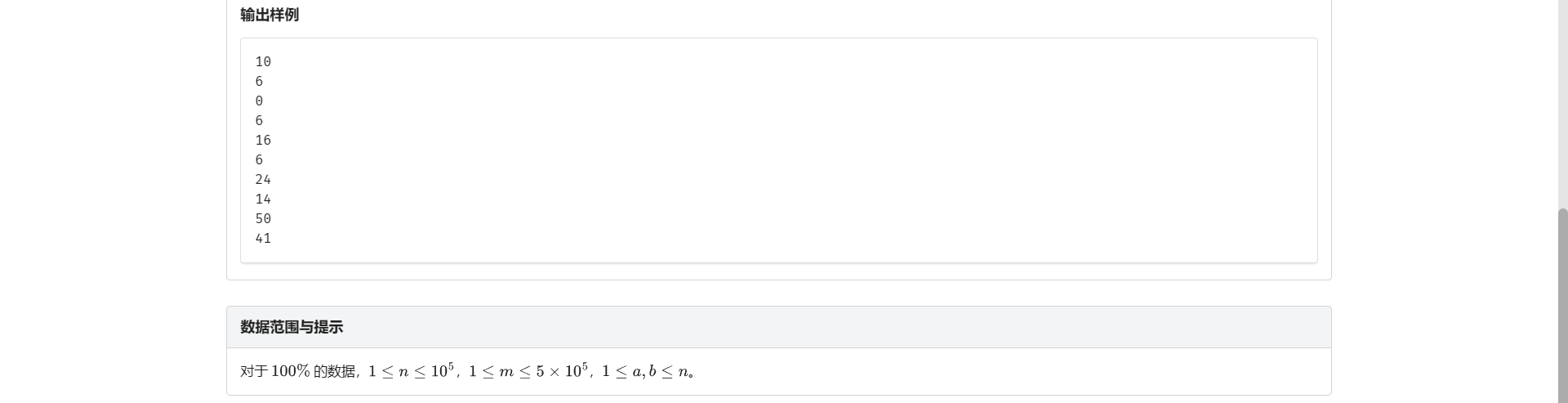
板子 详见线段树学习笔记
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define ls (k << 1)
#define rs (k << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
const int N = 1e6 + 0721;
int sum[N];
int n, m;
void update(int k, int l, int r, int v, int val) {
if (l == r) {
sum[k] += val;
return;
}
if (v <= mid)
update(ls, l, mid, v, val);
else
update(rs, mid + 1, r, v, val);
sum[k] = sum[ls] + sum[rs];
}
int query(int k, int l, int r, int u, int v) {
if (u <= l && r <= v)
return sum[k];
int res = 0;
if (u <= mid)
res += query(ls, l, mid, u, v);
if (v > mid)
res += query(rs, mid + 1, r, u, v);
return res;
}
signed main() {
scanf("%lld%lld", &n, &m);
while (m--) {
int opt, x, y;
scanf("%lld%lld%lld", &opt, &x, &y);
if (opt == 0)
update(1, 1, n, x, y);
else
printf("%lld\n", query(1, 1, n, x, y));
}
return 0;
}
B.区间查改
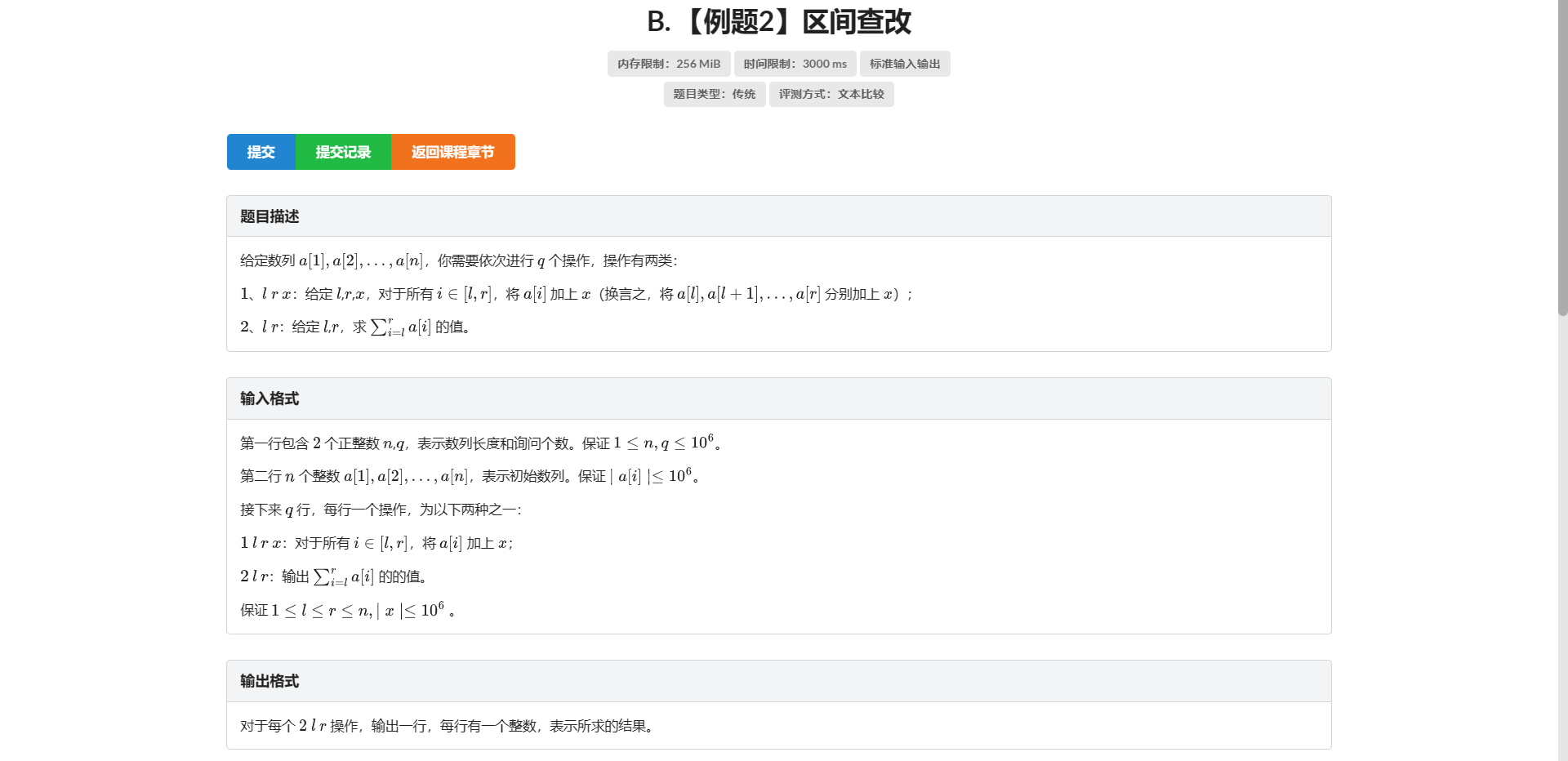
怎么还是板子啊
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define mid ((l + r) >> 1)
#define ls (k << 1)
#define rs (k << 1 | 1)
using namespace std;
const int N = 5e6 + 0721;
int a[N];
ll sum[N], lazy[N];
int n, m;
inline void pushup(int k) { sum[k] = sum[ls] + sum[rs]; }
inline void ad(int k, int l, int r, int val) {
sum[k] += 1ll * val * (r - l + 1);
lazy[k] += val;
}
inline void pushdown(int k, int l, int r) {
ad(ls, l, mid, lazy[k]);
ad(rs, mid + 1, r, lazy[k]);
lazy[k] = 0;
}
void build(int k, int l, int r) {
if (l == r) {
sum[k] = a[l];
return;
}
build(ls, l, mid);
build(rs, mid + 1, r);
pushup(k);
}
void modify(int k, int l, int r, int u, int v, int val) {
if (u <= l && r <= v) {
ad(k, l, r, val);
return;
}
pushdown(k, l, r);
if (u <= mid)
modify(ls, l, mid, u, v, val);
if (v > mid)
modify(rs, mid + 1, r, u, v, val);
pushup(k);
}
ll query(int k, int l, int r, int u, int v) {
if (u <= l && r <= v)
return sum[k];
pushdown(k, l, r);
ll res = 0;
if (u <= mid)
res += query(ls, l, mid, u, v);
if (v > mid)
res += query(rs, mid + 1, r, u, v);
pushup(k);
return res;
}
int main() {
// freopen("1.txt", "r", stdin);
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
build(1, 1, n);
while (m--) {
int opt, l, r, x;
scanf("%d%d%d", &opt, &l, &r);
if (opt == 1) {
scanf("%d", &x);
modify(1, 1, n, l, r, x);
} else
printf("%lld\n", query(1, 1, n, l, r));
}
return 0;
}
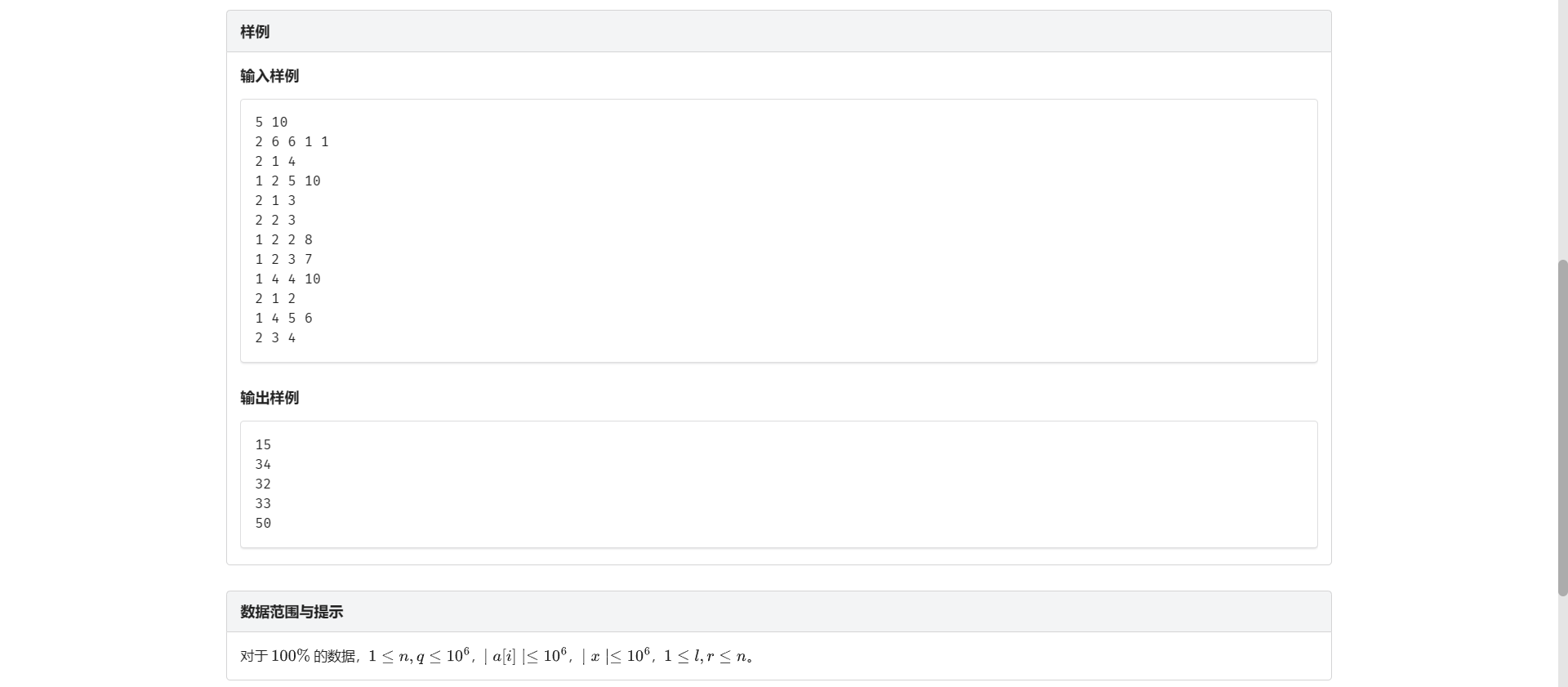
C.公园遛狗
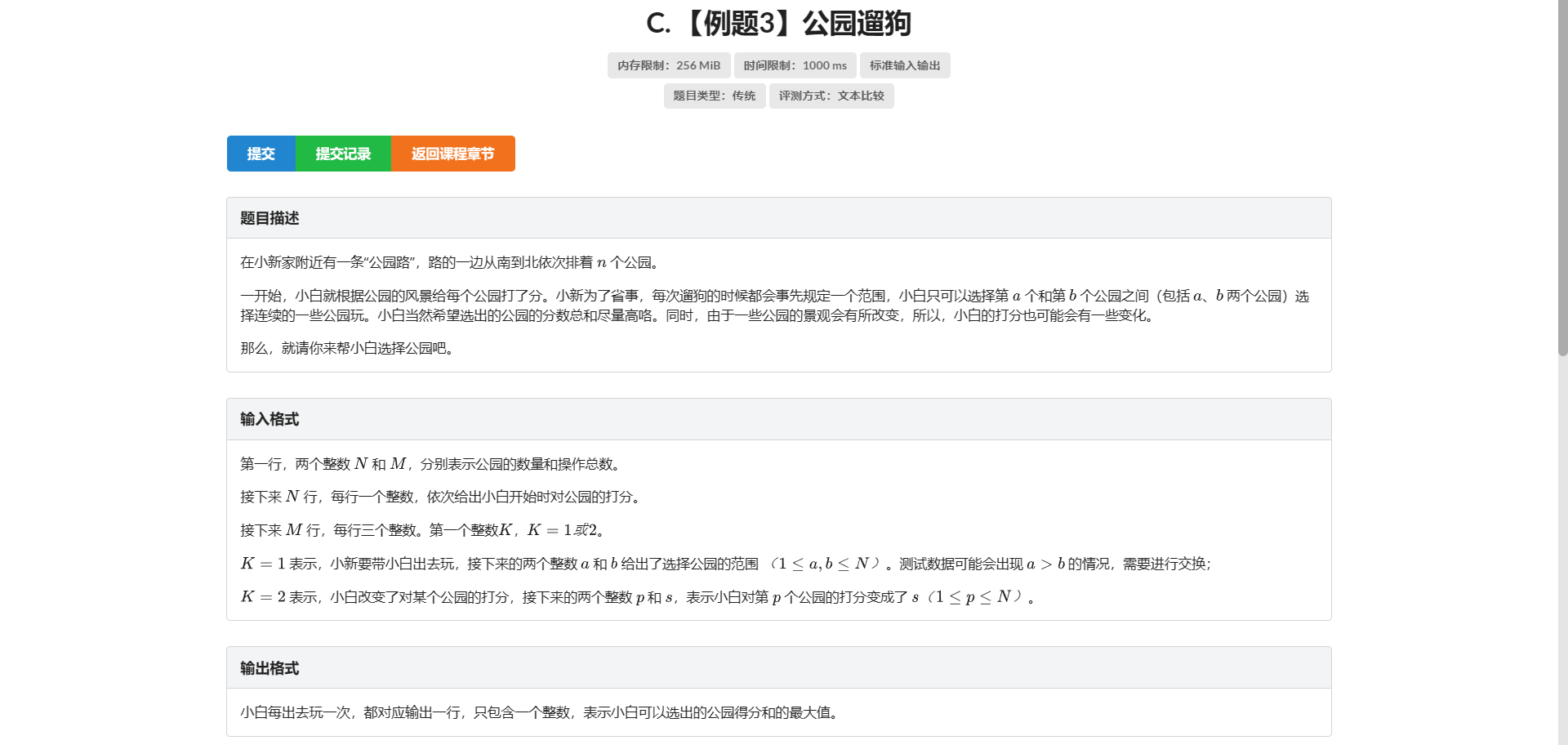
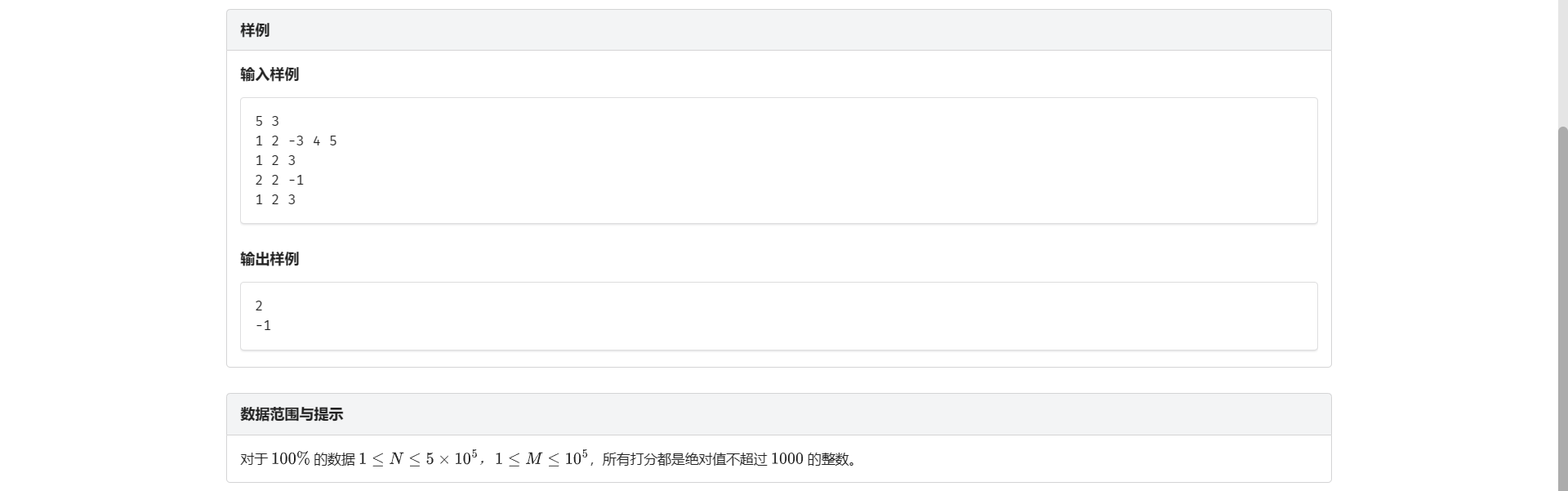
单点修改非常简单 问题在于如何查询最大子区间和
我们考虑分治的特点 一段区间的最大子区间和可能只在左儿子 只在右儿子 或者在跨越中点的一段区间
所以我们除了维护各自区间内部的最大子段 还要维护其区间包括左/右边界的最大子段
由于这题只是单点修改 所以我们只需要考虑上传操作
首先区间内部最大子段非常好维护 只要左右儿子内部区间和左儿子包含右端点区间+右儿子包含左端点区间三个取最大值
但是发现左/右边界 可能是左儿子/右儿子的左/右边界 也可能是左儿子/右儿子的全部+右儿子/左儿子的左/右边界
所以我们还需要维护整段区间的和
点击查看代码
#include <bits/stdc++.h>
#define mid ((l + r) >> 1)
#define ls (k << 1)
#define rs (k << 1 | 1)
using namespace std;
const int N = 5e5 + 0721;
int a[N];
//int sum[N << 2], lmax[N << 2], rmax[N << 2], maxx[N << 2];
int n, m;
struct node {
int sum, lmax, rmax, maxx;
} tr[N << 2];
inline void pushup(int k) {
tr[k].sum = tr[ls].sum + tr[rs].sum;
tr[k].lmax = max(tr[ls].lmax, tr[ls].sum + tr[rs].lmax);
tr[k].rmax = max(tr[rs].rmax, tr[rs].sum + tr[ls].rmax);
tr[k].maxx = max(tr[ls].maxx, tr[rs].maxx);
tr[k].maxx = max(tr[k].maxx, tr[ls].rmax + tr[rs].lmax);
}
node cmb(node x, node y) {
node z;
z.sum = x.sum + y.sum;
z.lmax = max(x.lmax, x.sum + y.lmax);
z.rmax = max(y.rmax, y.sum + x.rmax);
z.maxx = max(x.maxx, y.maxx);
z.maxx = max(z.maxx, x.rmax + y.lmax);
return z;
}
void build(int k, int l, int r) {
if(l == r) {
tr[k].sum = tr[k].lmax = tr[k].rmax = tr[k].maxx = a[l];
return;
}
build(ls, l, mid);
build(rs, mid + 1, r);
pushup(k);
}
void update(int k, int l, int r, int loc, int val) {
if (l == r) {
tr[k].sum = tr[k].lmax = tr[k].rmax = tr[k].maxx = val;
return;
}
if (loc <= mid)
update(ls, l, mid, loc, val);
else
update(rs, mid + 1, r, loc, val);
pushup(k);
}
node query(int k, int l, int r, int u, int v) {
if (u <= l && v >= r)
return tr[k];
if (v <= mid)
return query(ls, l, mid, u, v);
else if (u > mid)
return query(rs, mid + 1, r, u, v);
else {
node x = query(ls, l, mid, u, v);
node y = query(rs, mid + 1, r, u, v);
return cmb(x, y);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
build(1, 1, n);
while (m--) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
if (x == 1) {
if (y > z)
swap(y, z);
printf("%d\n",query(1, 1, n, y, z).maxx);
}
else
update(1, 1, n, y, z);
}
return 0;
}
D.维护序列
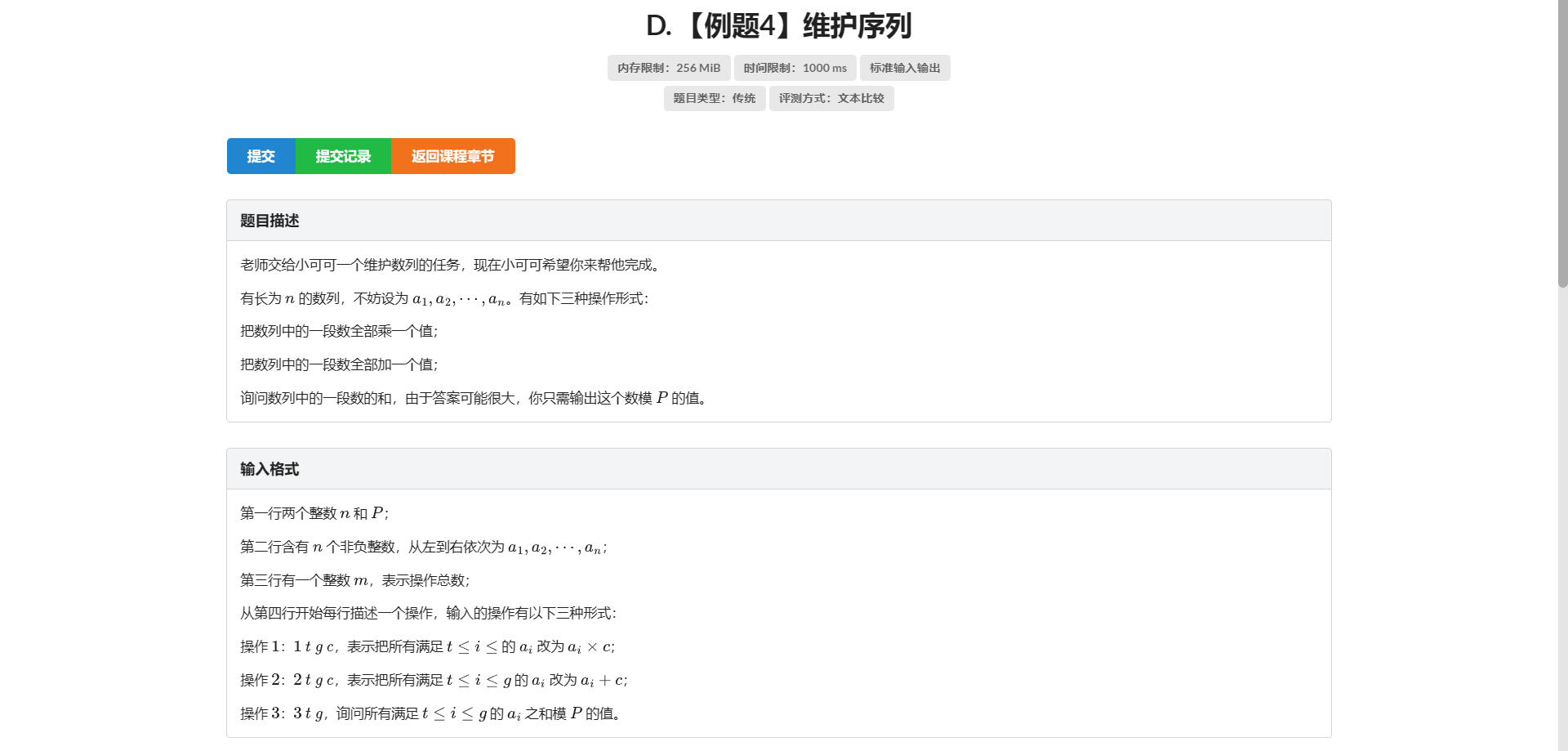

主要考察懒标记的使用
很容易想到开两个懒标记 但是问题在于如何下传懒标记
首先你改变乘法懒标记是要一起变加法标记的
可能会想不变 下传的时候再说
那假如说我在这之前对这个区间依次进行了 \(+1 *3 +1 *3\) 四个操作
那怎么判断哪些加数要乘多少?显然没法做
所以我们选择每次修改乘法标记的时候顺便把加法改了 记录子区间总共还有多少没加
下传时 因为这个加数已经是被乘了正确倍数的 所以让子区间先乘乘法懒标记再加上加法懒标记
这道题提醒我们有多个懒标记时一定要想到各个懒标记之间的影响
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define ls (k << 1)
#define rs (k << 1 | 1)
#define mid (l + r >> 1)
using namespace std;
const int N = 500721;
int s[N], a[N], lazy1[N], lazy2[N];
int n, m, p;
void built(int k, int l, int r) {
lazy2[k] = 1;
if (l == r) {
s[k] = a[l];
return;
}
built(ls, l, mid);
built(rs, mid + 1, r);
s[k] = (s[ls] + s[rs]) % p;
return;
}
void adl(int k, int l, int r, int v1, int v2) {
s[k] = ((s[k] * v2) % p + v1 * (r - l + 1) % p) % p;
lazy1[k] = (lazy1[k] * v2 % p + v1) % p;
lazy2[k] = lazy2[k] * v2 % p;
return;
}
inline void pushup(int k) { s[k] = (s[ls] + s[rs]) % p; }
void pushdown(int k, int l, int r) {
adl(ls, l, mid, lazy1[k], lazy2[k]);
adl(rs, mid + 1, r, lazy1[k], lazy2[k]);
lazy1[k] = 0;
lazy2[k] = 1;
}
void jia(int k, int l, int r, int x, int y, int v) {
if (x <= l && y >= r) {
adl(k, l, r, v, 1);
return;
}
pushdown(k, l, r);
if (x <= mid)
jia(ls, l, mid, x, y, v);
if (y > mid)
jia(rs, mid + 1, r, x, y, v);
pushup(k);
}
void cheng(int k, int l, int r, int x, int y, int v) {
if (x <= l && y >= r) {
adl(k, l, r, 0, v);
return;
}
pushdown(k, l, r);
if (x <= mid)
cheng(ls, l, mid, x, y, v);
if (y > mid)
cheng(rs, mid + 1, r, x, y, v);
pushup(k);
}
int cx(int k, int l, int r, int x, int y) {
if (x <= l && y >= r) {
return s[k];
}
pushdown(k, l, r);
int res = 0;
if (x <= mid)
res = (res + cx(ls, l, mid, x, y)) % p;
if (y > mid)
res = (res + cx(rs, mid + 1, r, x, y)) % p;
pushup(k);
res = res % p;
return res;
}
signed main() {
// freopen("1.txt", "r", stdin);
scanf("%lld%lld", &n, &p);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
scanf("%lld", &m);
built(1, 1, n);
for (int i = 1; i <= m; ++i) {
int num;
scanf("%lld", &num);
if (num == 1) {
int x, y, v;
scanf("%lld%lld%lld", &x, &y, &v);
cheng(1, 1, n, x, y, v);
} else if (num == 2) {
int x, y, v;
scanf("%lld%lld%lld", &x, &y, &v);
jia(1, 1, n, x, y, v);
} else {
int x, y;
scanf("%lld%lld", &x, &y);
printf("%lld\n", cx(1, 1, n, x, y));
}
}
return 0;
}
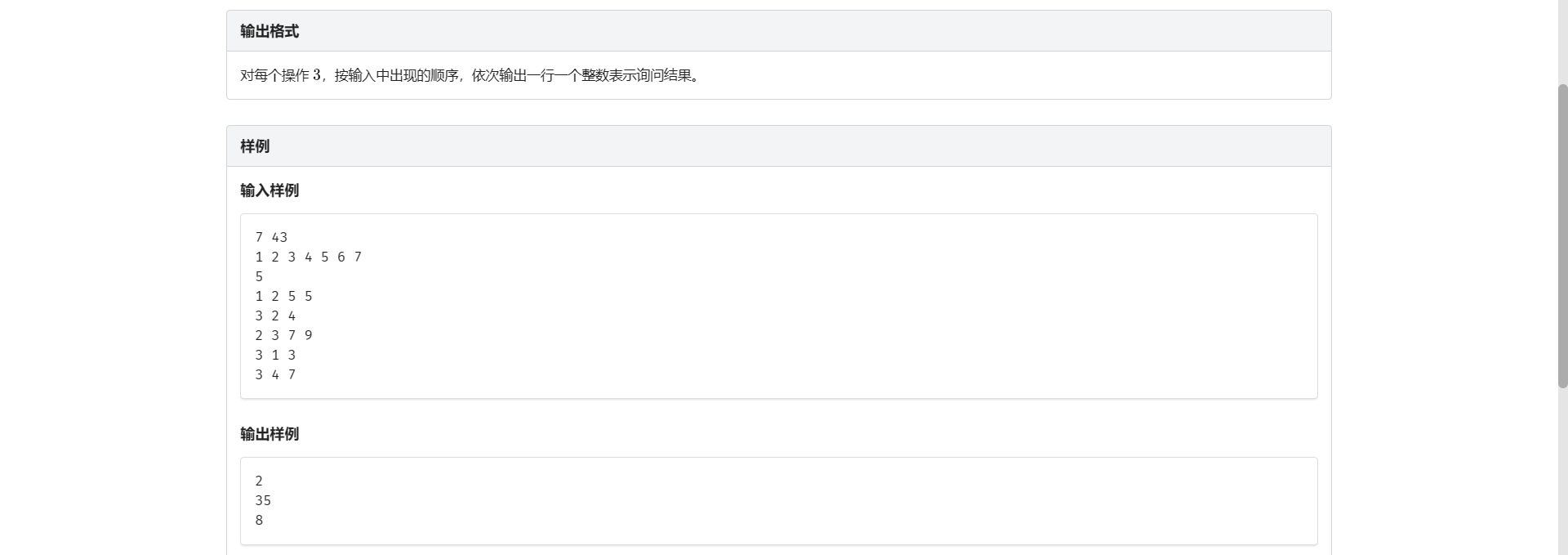
F.取模问题
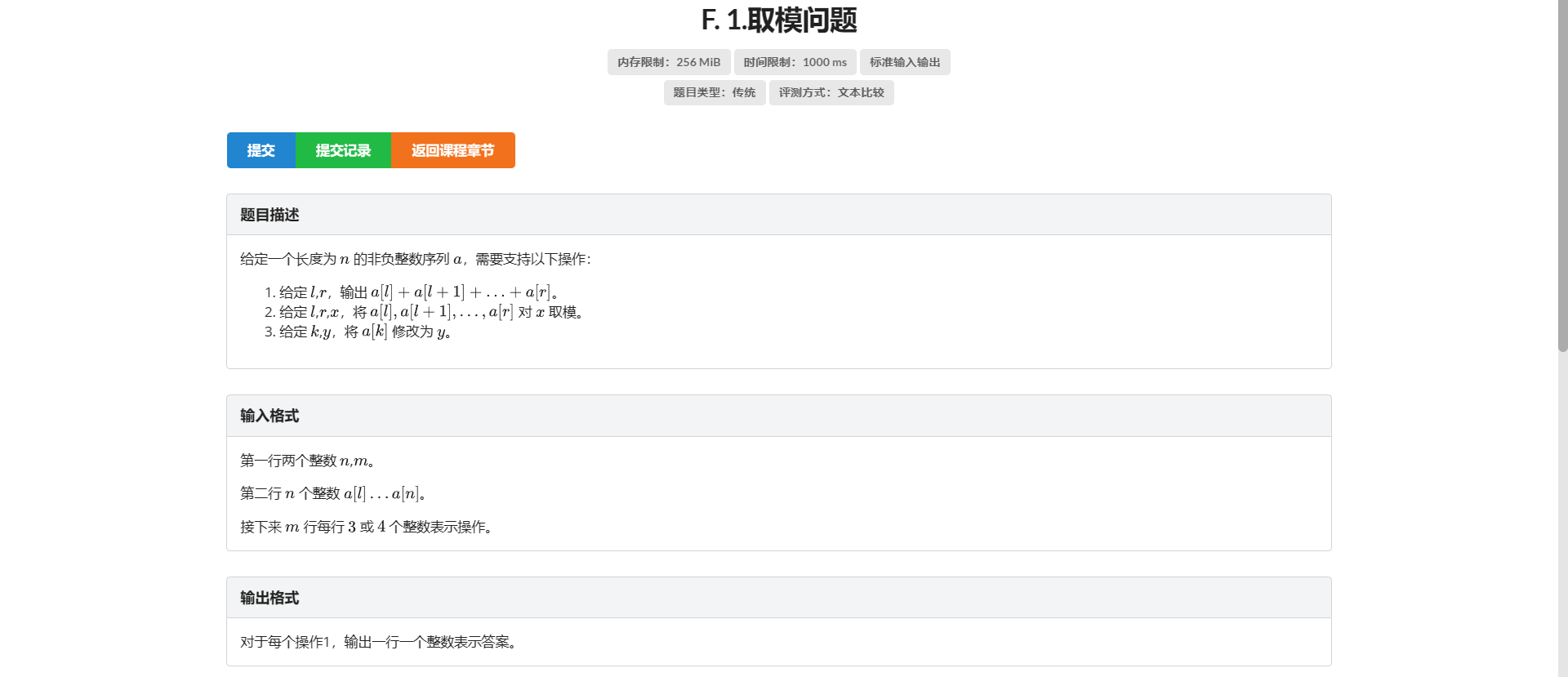
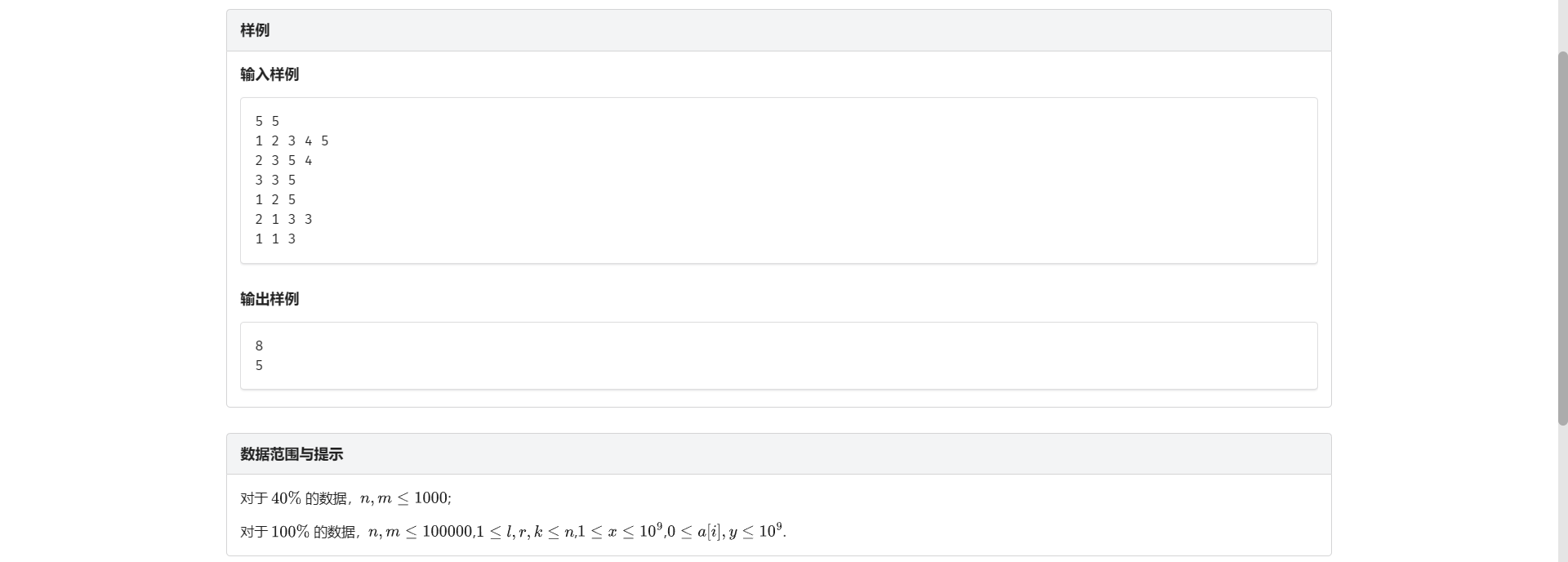
想到记录区间最大值 如果最大值小于这个模数那么就直接 return 没必要取模
但是好像也只是一个常数优化
结果上网找了一下正解好像就是这个 非常震惊
下面补一个我自己的复杂度证明:
首先要证明这样一件事
- 对于一个数 \(x\) 给它对任意小于它的数取模后的最大值不超过 \(\frac{x}{2}\)
很直觉的一个结论 但是确实可以证明它
分讨
如果 \(mod \le \frac{x}{2}\) 结果一定 \(< mod\) 进而 \(\le \frac{x}{2}\)
如果 \(mod > \frac{x}{2}\) 其结果一定为 \(x - mod\)(因为\(\left\lfloor\dfrac{x}{mod}\right\rfloor\) 一定为 \(1\))那么结果显然也 \(\le \frac{x}{2}\)
这就说明 对于一个 \(x\) 而言 最多只需要取模 \(\log\) 次
那么如果没有单点修改操作 每个数最多被取模 \(\log\) 次 复杂度就是 \(\text{O}(n \log V)\)
那么每次单点修改产生的新 \(x\) 最多需要 \(\log\) 次才会被“模尽”
那么我们“模尽”一次单点修改所需要的复杂度就是 \(\log ^2 V\)
但因为每次修改的 \(x\) 需要 \(\log\) 次才会被“模尽” 所以如果每次都让一个修改“模尽”的话 修改操作最多只会出现 \(\frac{n}{\log V}\) 次
那么整体复杂度就还是 \(\log ^2 V \times \frac{n}{\log V} = \text{O}(n \log V)\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define ls (k << 1)
#define rs (k << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
namespace steven24 {
const int N = 3e5 + 0721;
int a[N];
int n, m;
struct segment_tree {
int tr[N << 2];
ll sum[N << 2];
inline void pushup(int k) {
tr[k] = max(tr[ls], tr[rs]);
sum[k] = sum[ls] + sum[rs];
}
void build(int k, int l, int r) {
if (l == r) {
tr[k] = sum[k] = a[l];
return;
}
build(ls, l, mid);
build(rs, mid + 1, r);
pushup(k);
}
void modify(int k, int l, int r, int u, int v, int mod) {
if (mod > tr[k]) {
return;
}
if (l == r) {
tr[k] %= mod;
sum[k] = tr[k];
return;
}
if (u <= mid) modify(ls, l, mid, u, v, mod);
if (v > mid) modify(rs, mid + 1, r, u, v, mod);
pushup(k);
}
void update(int k, int l, int r, int loc, int val) {
if (l == r) {
tr[k] = sum[k] = val;
return;
}
if (loc <= mid) update(ls, l, mid, loc, val);
else update(rs, mid + 1, r, loc, val);
pushup(k);
}
ll query(int k, int l, int r, int u, int v) {
if (u <= l && v >= r) {
return sum[k];
}
ll ret = 0;
if (u <= mid) ret += query(ls, l, mid, u, v);
if (v > mid) ret += query(rs, mid + 1, r, u, v);
pushup(k);
return ret;
}
} seg;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 1) + (xr << 3) + (cr ^ 48), cr = getchar();
return xr * F;
}
void main() {
n = read(), m = read();
for (int i = 1; i <= n; ++i) a[i] = read();
seg.build(1, 1, n);
while (m--) {
int opt, l, r, x;
opt = read(), l = read(), r = read();
switch (opt) {
case 1 : {
printf("%lld\n", seg.query(1, 1, n, l, r));
break;
}
case 2 : {
x = read();
seg.modify(1, 1, n, l, r, x);
break;
}
default : {
seg.update(1, 1, n, l, r);
break;
}
}
}
}
}
int main() {
steven24::main();
return 0;
}
/*
5 5
1 2 3 4 5
2 3 5 4
3 3 5
1 2 5
2 1 3 3
1 1 3
*/
G.魔法传输
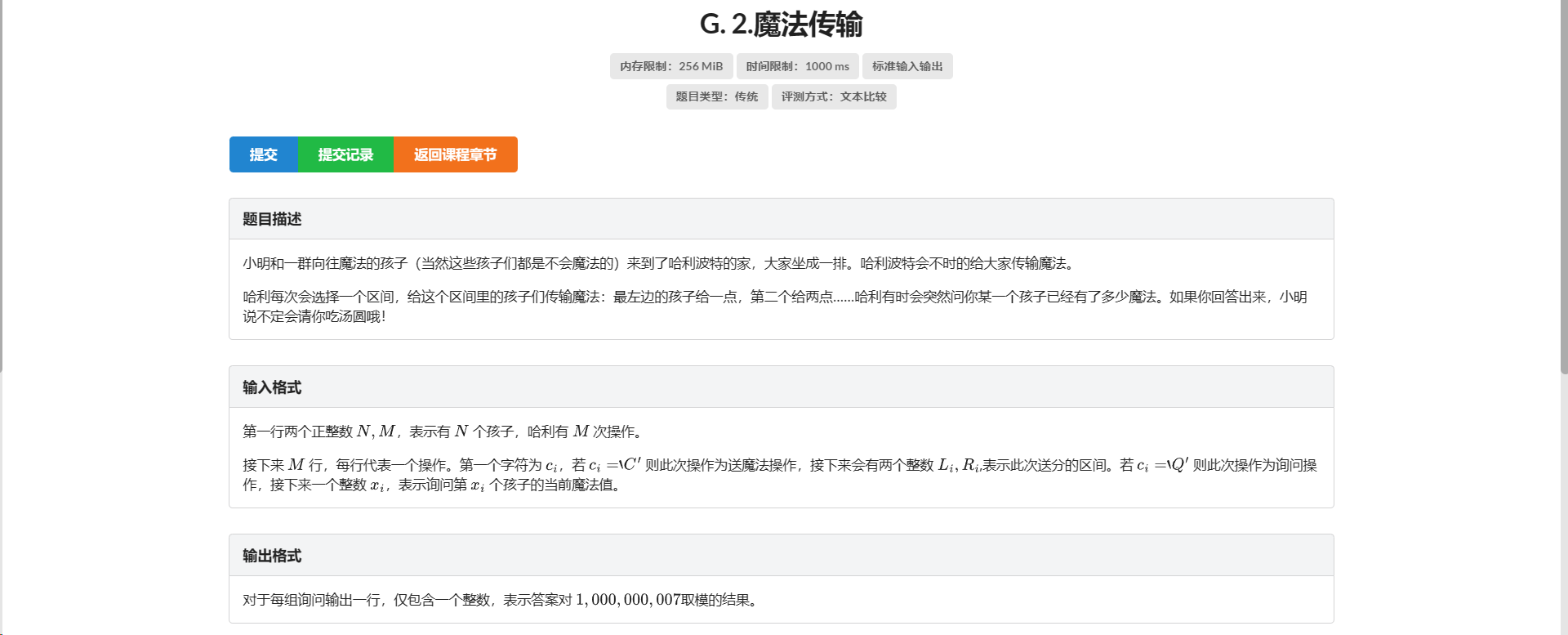
就。。。看起来就挺典的
每次区间修改就是 \(1, 2, 3, 4, 5, ...\)
把它们差分一下就全是 \(1\)
所以我们考虑线段树维护差分
正好这题还是单点查询 对应到线段树上就是区间查询
记得在 \(r + 1\) 处加上一个 \(-(r - l + 1)\) 来消除对后续数的影响
按理说需要负数取模 但这题没负数取模也过了(?
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define ls (k << 1)
#define rs (k << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
namespace steven24 {
const int N = 1e5 + 0721;
const int mod = 1e9 + 7;
int n, m;
struct segment_tree {
ll tr[N << 2], lazy[N << 2];
inline void add(int k, int l, int r, int val) {
tr[k] = (tr[k] + (r - l + 1) * val) % mod;
lazy[k] = (lazy[k] + val) % mod;
}
inline void pushdown(int k, int l, int r) {
add(ls, l, mid, lazy[k]);
add(rs, mid + 1, r, lazy[k]);
lazy[k] = 0;
}
inline void pushup(int k) {
tr[k] = (tr[ls] + tr[rs]) % mod;
}
void modify(int k, int l, int r, int u, int v, int val) {
if (u <= l && v >= r) {
add(k, l, r, val);
return;
}
if (lazy[k]) pushdown(k, l, r);
if (u <= mid) modify(ls, l, mid, u, v, val);
if (v > mid) modify(rs, mid + 1, r, u, v, val);
pushup(k);
}
ll query(int k, int l, int r, int u, int v) {
if (u <= l && v >= r) {
return tr[k];
}
if (lazy[k]) pushdown(k, l, r);
ll ret = 0;
if (u <= mid) ret = (ret + query(ls, l, mid, u, v)) % mod;
if (v > mid) ret = (ret + query(rs, mid + 1, r, u, v)) % mod;
pushup(k);
return ret;
}
} seg;
void main() {
scanf("%d%d", &n, &m);
memset(seg.tr, 0, sizeof seg.tr);
memset(seg.lazy, 0, sizeof seg.lazy);
while (m--) {
char opt;
int x, y;
scanf(" %c", &opt);
if (opt == 'C') {
scanf("%d%d", &x, &y);
seg.modify(1, 1, n, x, y, 1);
seg.modify(1, 1, n, y + 1, y + 1, -(y - x + 1));
} else {
scanf("%d", &x);
printf("%lld\n", seg.query(1, 1, n, 1, x));
}
}
}
}
int main() {
steven24::main();
return 0;
}
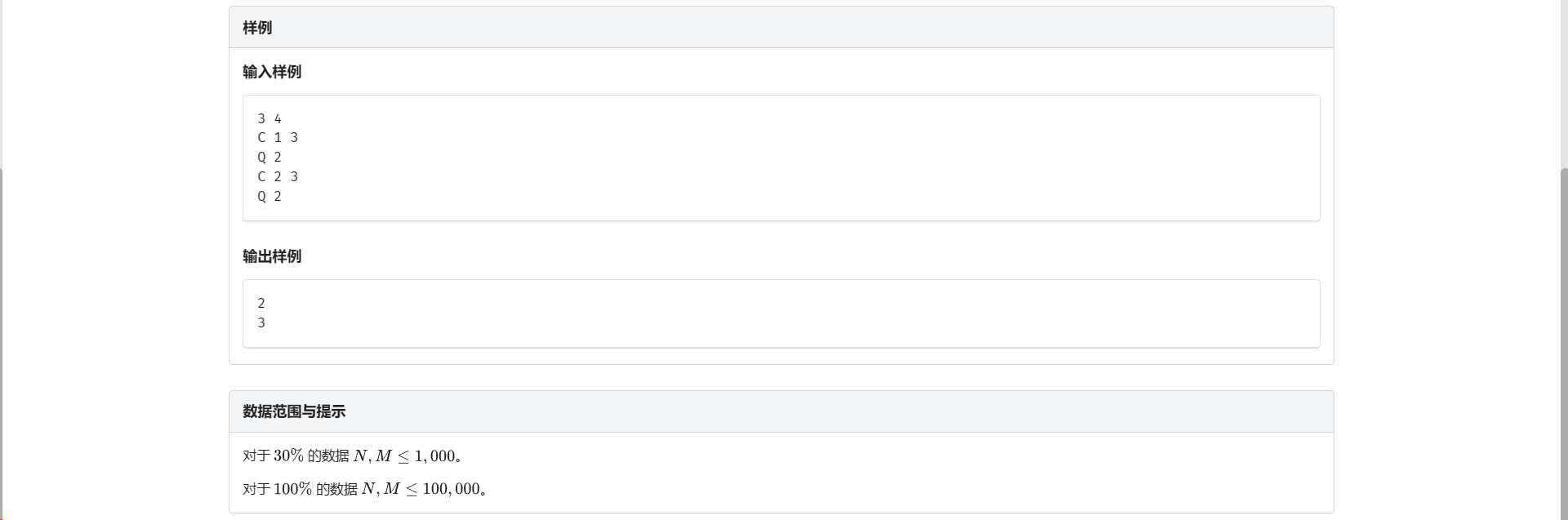
/*
3 4
C 1 3
Q 2
C 2 3
Q 2
*/
H.队伍整理
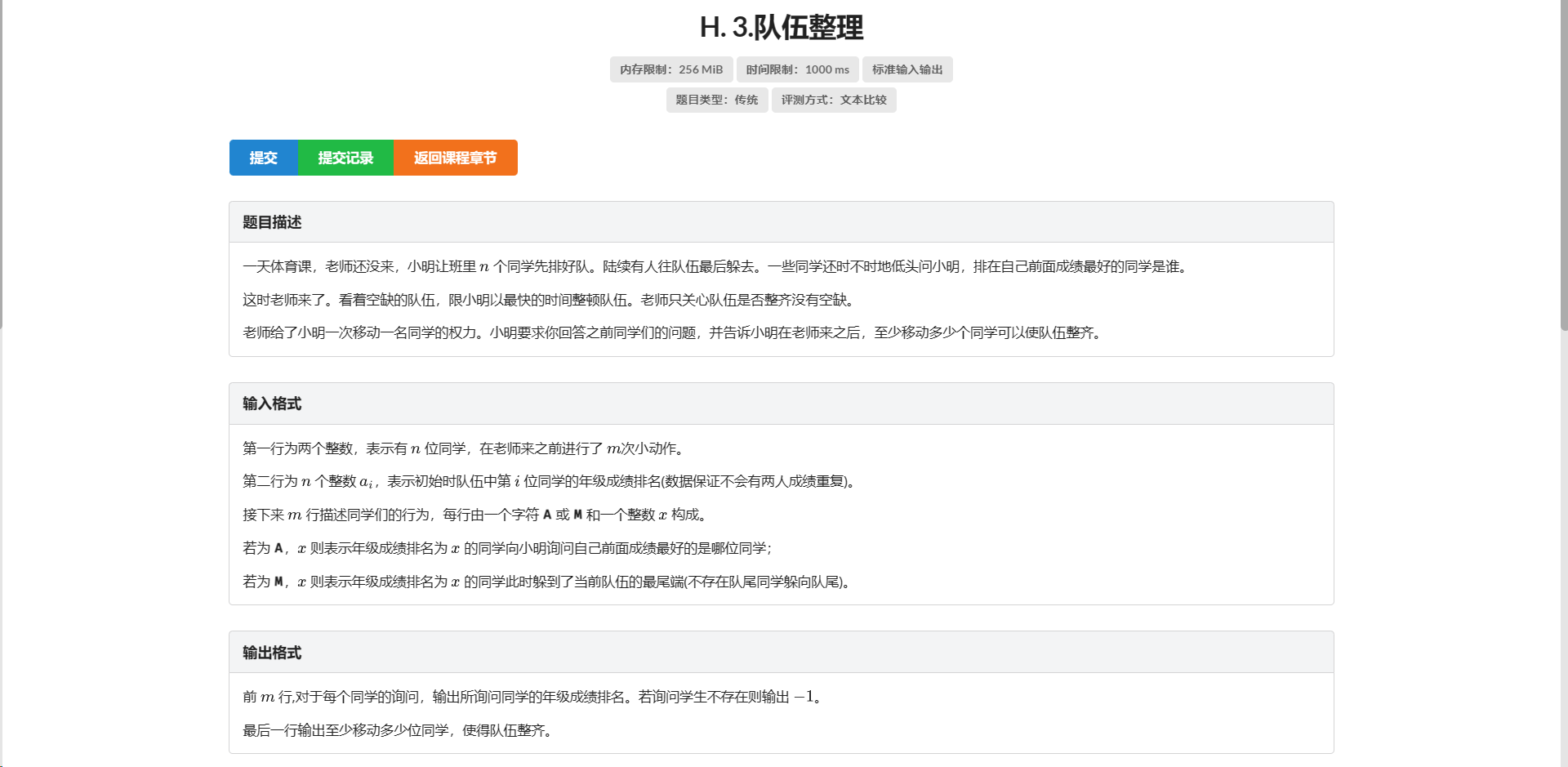
梦回书架
直接把空间开到 \(n + m\) 然后维护一个 \(prs\) 表示当前队尾的位置
再开一个 \(loc\) 数组表示当前权值的数的位置
这样对于每个跑到队尾的操作 直接 \(++prs\) 然后把它原来的位置变成 \(inf\) 把新位置变成它的权值 然后把它的 \(loc\) 改了
那么查询前面排名最高的就是一个查询前缀最小值操作
对于移动的询问 要么是我把前面的若干个人放到后面的空里 要么是我把后面的若干个人放到前面的空里
这样正着倒着扫两遍然后取 \(\min\) 即可 具体实现可以看代码
点击查看代码
#include <bits/stdc++.h>
#define ls (k << 1)
#define rs (k << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
namespace steven24 {
const int N = 2e5 + 5;
const int M = 1e7 + 5;
const int inf = 0x7fffffff;
int a[N];
int loc[M];
int n, m, prs;
struct segment_tree {
int tr[N << 2];
inline void pushup(int k) {
tr[k] = min(tr[ls], tr[rs]);
}
void build(int k, int l, int r) {
if (l == r) {
tr[k] = a[l];
return;
}
build(ls, l, mid);
build(rs, mid + 1, r);
pushup(k);
}
void modify(int k, int l, int r, int loc, int val) {
if (l == r) {
tr[k] = val;
return;
}
if (loc <= mid) modify(ls, l, mid, loc, val);
else modify(rs, mid + 1, r, loc, val);
pushup(k);
}
int query(int k, int l, int r, int u, int v) {
if (u <= l && v >= r) {
return tr[k];
}
int ret = inf;
if (u <= mid) ret = min(ret, query(ls, l, mid, u, v));
if (v > mid) ret = min(ret, query(rs, mid + 1, r, u, v));
pushup(k);
return ret;
}
} seg;
void main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
loc[a[i]] = i;
}
seg.build(1, 1, (int)2e5);
prs = n;
while (m--) {
int x;
char opt;
scanf(" %c%d", &opt, &x);
if (opt == 'A') {
if (loc[x] == 0) printf("-1\n");
else if (1 <= loc[x] - 1 && seg.query(1, 1, (int)2e5, 1, loc[x] - 1) != inf) printf("%d\n", seg.query(1, 1, (int)2e5, 1, loc[x] - 1));
else printf("-1\n");
}
else {
seg.modify(1, 1, (int)2e5, loc[x], inf);
a[loc[x]] = inf;
loc[x] = ++prs;
a[loc[x]] = x;
seg.modify(1, 1, (int)2e5, loc[x], x);
}
}
int cnt = 0;
int ans1 = 0;
for (int i = prs + 1; i <= (int)2e5; ++i) a[i] = inf;
for (int i = 1; i <= (int)2e5; ++i) {
if (a[i] != inf) ++cnt;
if (cnt && a[i] == inf) {
++ans1;
++cnt;
}
if (cnt == n) break;
}
cnt = 0;
int ans2 = 0;
for (int i = (int)2e5; i; --i) {
if (a[i] != inf) ++cnt;
if (cnt && a[i] == inf) {
++ans2;
++cnt;
}
if (cnt == n) break;
}
printf("%d\n", min(ans1, ans2));
}
}
int main() {
steven24::main();
return 0;
}
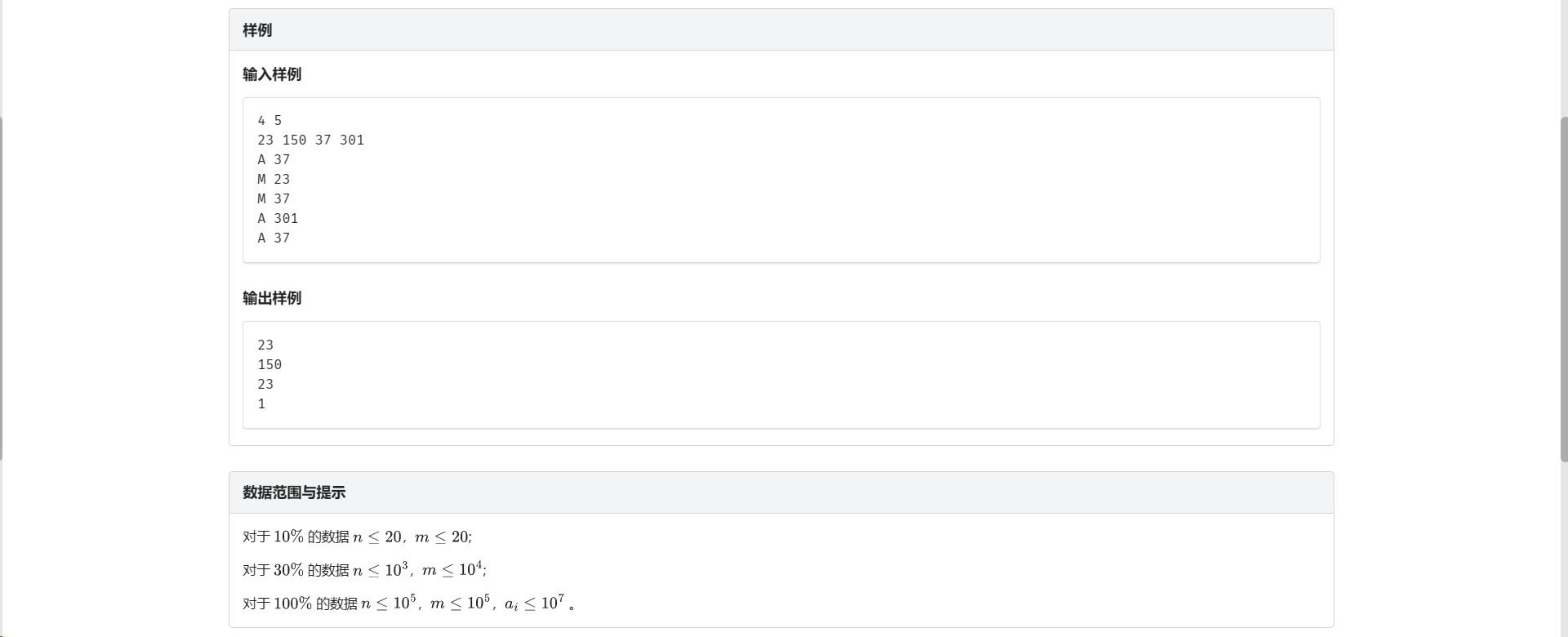
/*
4 5
23 150 37 301
A 37
M 23
M 37
A 301
A 37
*/
I.和或异或
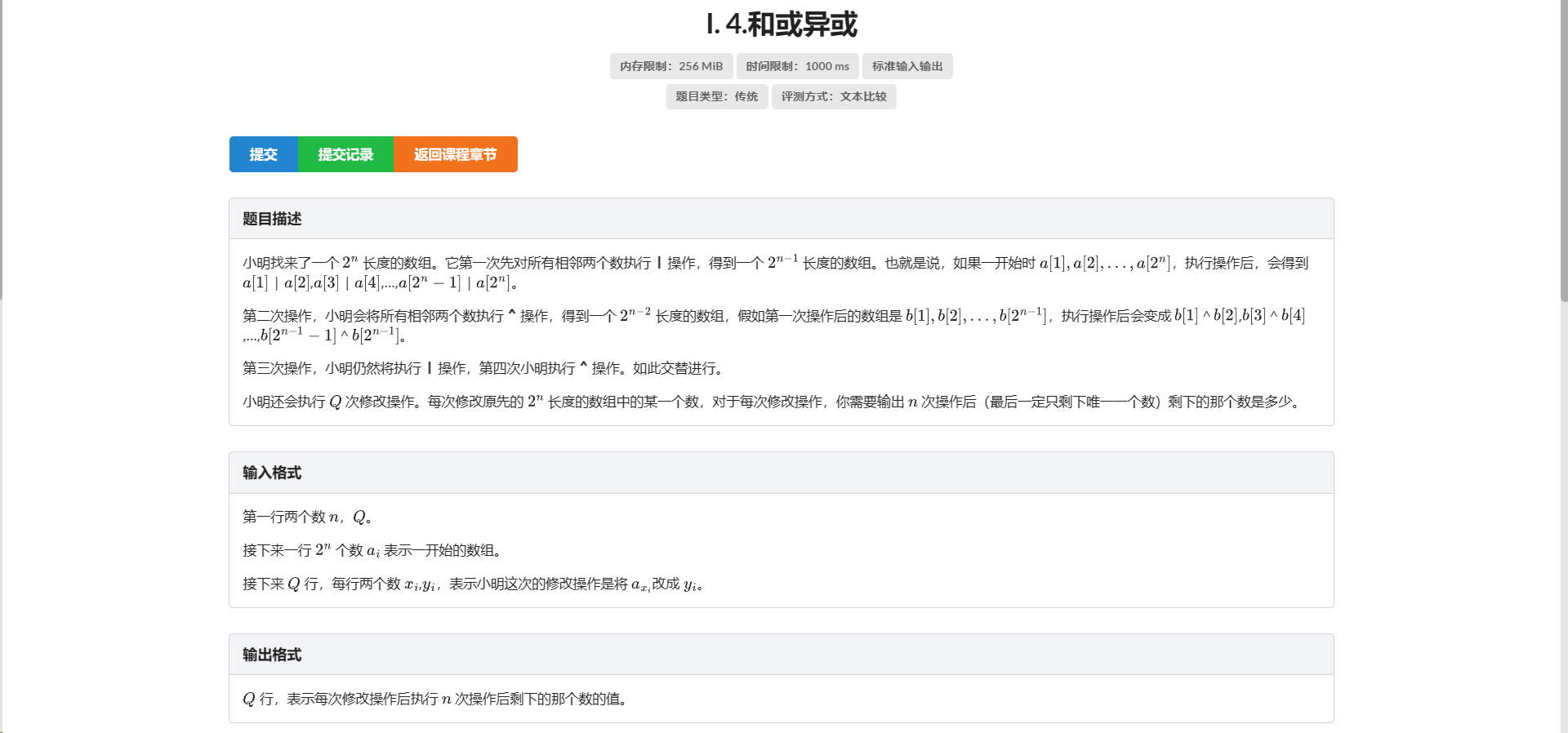
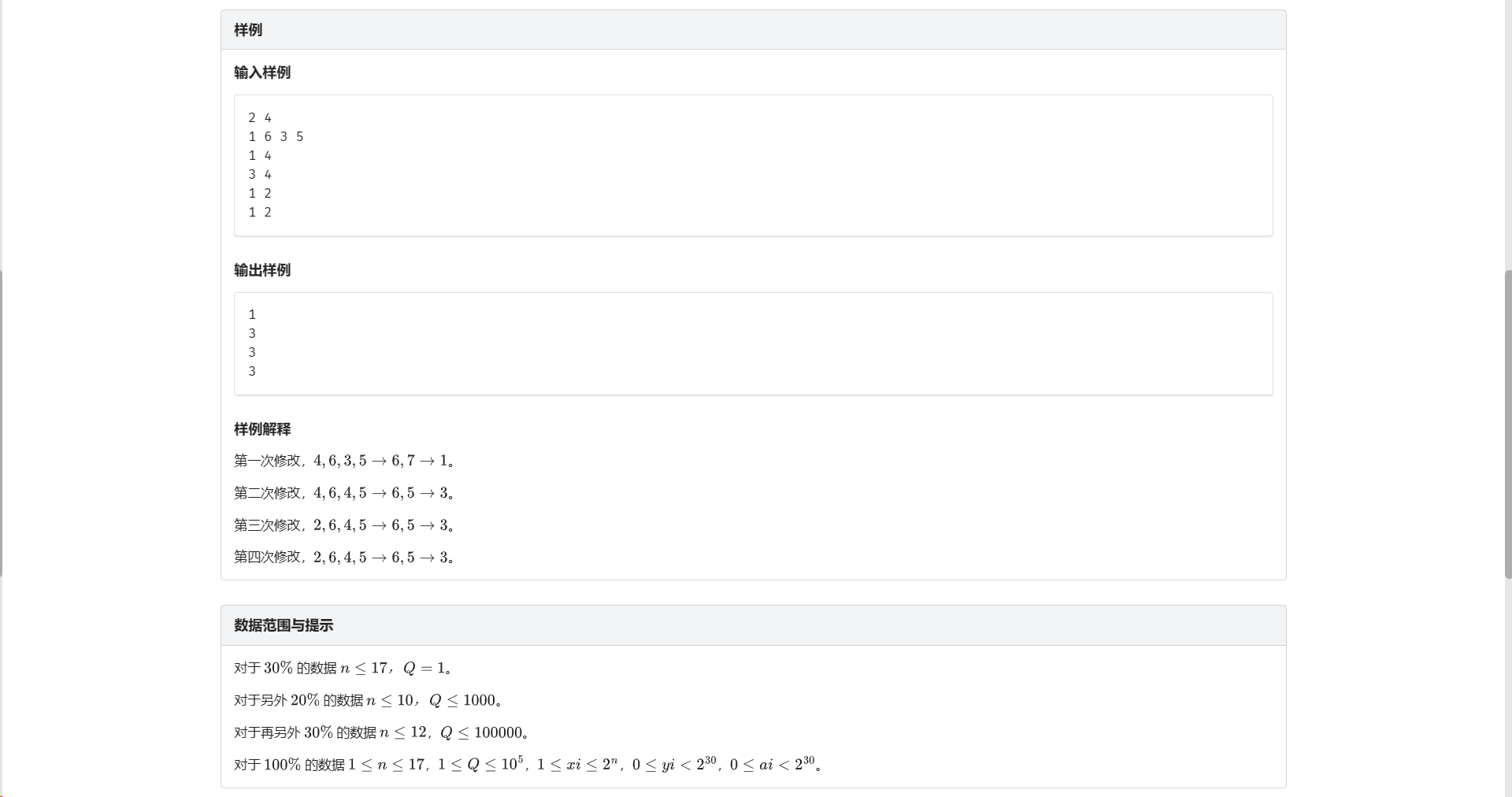
手搓一下就会发现这个结构很像线段树
正好单点修改只会修改 \(\log\) 个点
唯一的区别就是在于不同层之间合并(即 pushup)操作可能不同
那么我们额外记录一维 \(pos\) 表示当前层的 pushup 操作是取异或还是或
然后我们再手搓一下 不难发现最后一层的 pushup 操作取决于 \(n\) 的奇偶
如果 \(n\) 为奇数 最后一层就是或 否则就是异或
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 2e5 + 0721;
int a[N];
int n, q;
struct segment_tree {
#define ls (k << 1)
#define rs (k << 1 | 1)
#define mid ((l + r) >> 1)
int tr[N << 2];
inline void pushup(int k, bool pos) {
if (pos) tr[k] = tr[ls] | tr[rs];
else tr[k] = tr[ls] ^ tr[rs];
}
void build(int k, int l, int r, bool pos) {
if (l == r) {
tr[k] = a[l];
return;
}
build(ls, l, mid, !pos);
build(rs, mid + 1, r, !pos);
pushup(k, pos);
}
void modify(int k, int l, int r, int loc, int val, bool pos) {
if (l == r) {
tr[k] = val;
return;
}
if (loc <= mid) modify(ls, l, mid, loc, val, !pos);
else modify(rs, mid + 1, r, loc, val, !pos);
pushup(k, pos);
}
} seg;
void main() {
scanf("%d%d", &n, &q);
for (int i = 1; i <= (1 << n); ++i) scanf("%d", &a[i]);
bool pos = (n & 1);
n = (1 << n);
seg.build(1, 1, n, pos);
while (q--) {
int x, y;
scanf("%d%d", &x, &y);
seg.modify(1, 1, n, x, y, pos);
printf("%d\n", seg.tr[1]);
}
}
}
int main() {
steven24::main();
return 0;
}
/*
2 4
1 6 3 5
1 4
3 4
1 2
1 2
*/
J.括号匹配
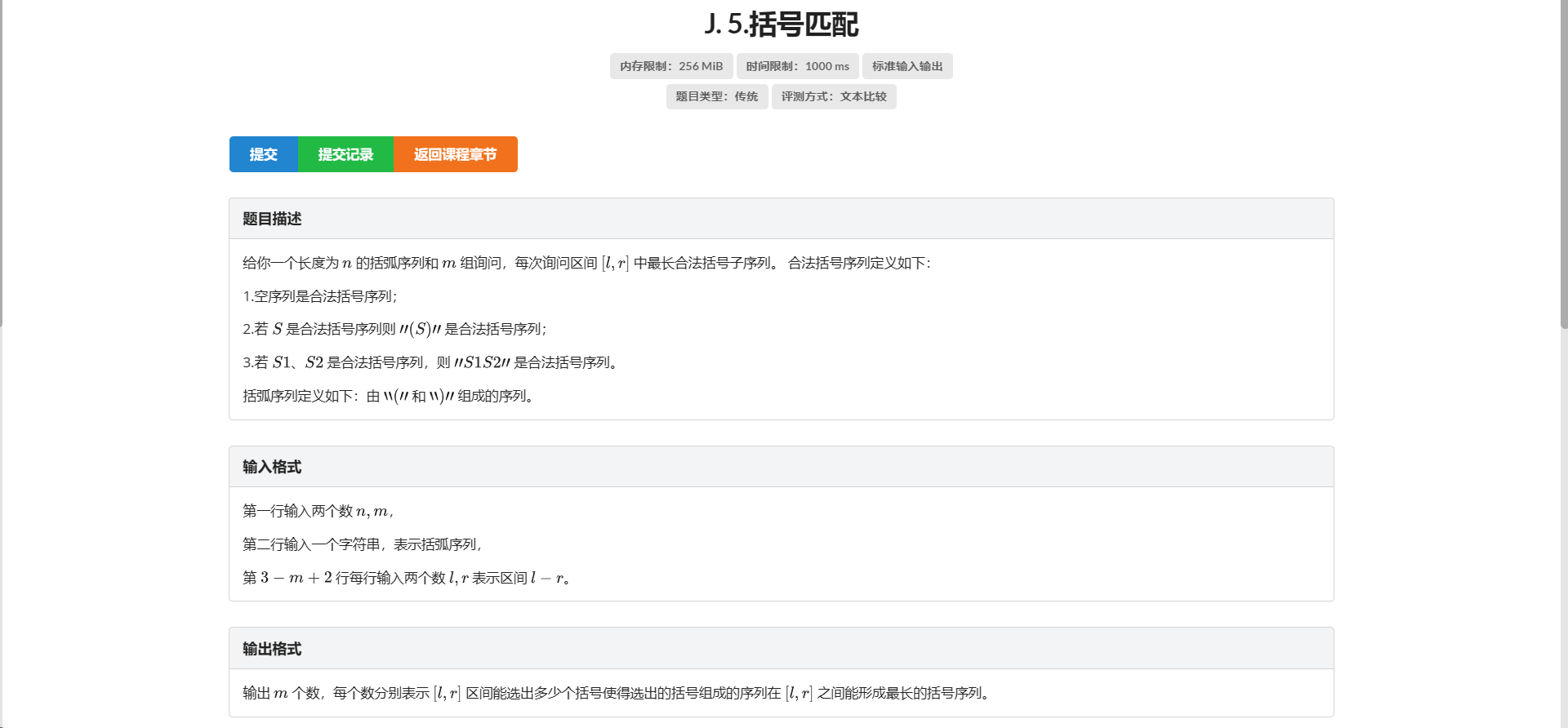
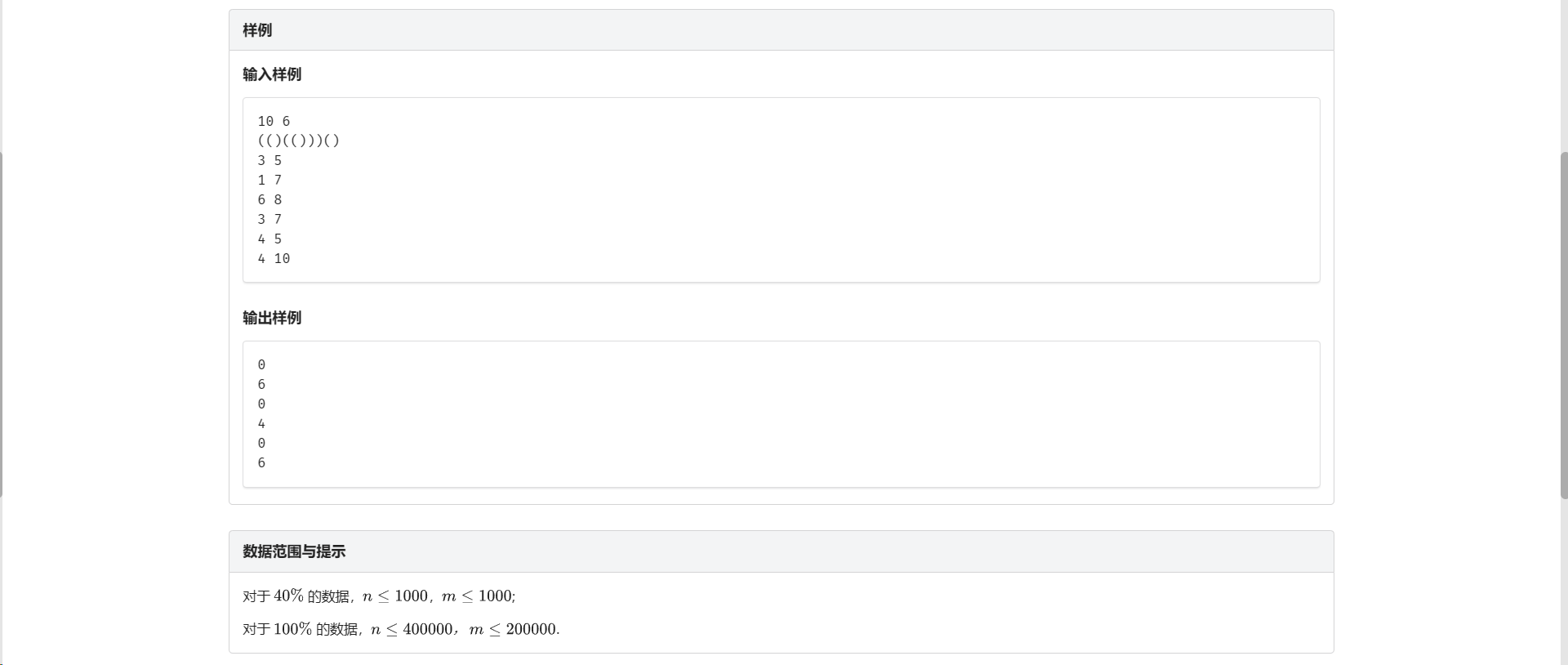
想麻烦了。
不难想到就是小白逛公园状物 考虑维护每个区间靠右未匹配的左括号数量 和靠左未匹配的右括号数量
然后实际上因为这个区间内所有未匹配的左括号 给它在右区间足够数量的右括号 一定能构成合法的括号匹配
因为你的区间一定长这样:
未匹配的右括号 - \(...\) - 未匹配的左括号
所以实质上上面那个东西就转化为了当前区间内未匹配的左括号/有括号数量了
考虑区间合并 一定是左区间未匹配的左括号数量与右区间未匹配的右括号的数量取 \(\min\) 构成新的合法匹配括号对
然后就没啥了
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 4e5 + 0721;
string s;
int n, m;
struct segment_tree {
#define ls (k << 1)
#define rs (k << 1 | 1)
#define mid ((l + r) >> 1)
struct node {
int res, lc, rc;
} tr[N << 2];
node merge(node x, node y) {
node ret = (node){0, 0, 0};
ret.lc = x.lc + y.lc - min(x.lc, y.rc);
ret.rc = x.rc + y.rc - min(x.lc, y.rc);
ret.res = x.res + y.res + min(x.lc, y.rc);
return ret;
}
void pushup(int k) {
tr[k] = merge(tr[ls], tr[rs]);
}
void build(int k, int l, int r) {
if (l == r) {
if (s[l - 1] == '(') tr[k].lc = 1;
else tr[k].rc = 1;
return;
}
build(ls, l, mid);
build(rs, mid + 1, r);
pushup(k);
}
node query(int k, int l, int r, int u, int v) {
if (u <= l && v >= r) {
return tr[k];
}
node ret = (node){0, 0, 0};
if (u <= mid) ret = merge(ret, query(ls, l, mid, u, v));
if (v > mid) ret = merge(ret, query(rs, mid + 1, r, u, v));
return ret;
}
} seg;
void main() {
ios::sync_with_stdio(false);
cin >> n >> m;
cin >> s;
seg.build(1, 1, n);
while (m--) {
int l, r;
cin >> l >> r;
cout << seg.query(1, 1, n, l, r).res * 2 << "\n";
}
}
}
int main() {
steven24::main();
return 0;
}
/*
10 6
(()(()))()
3 5
1 7
6 8
3 7
4 5
4 10
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号