YBTOJ 4.3RMQ问题
A.数列区间
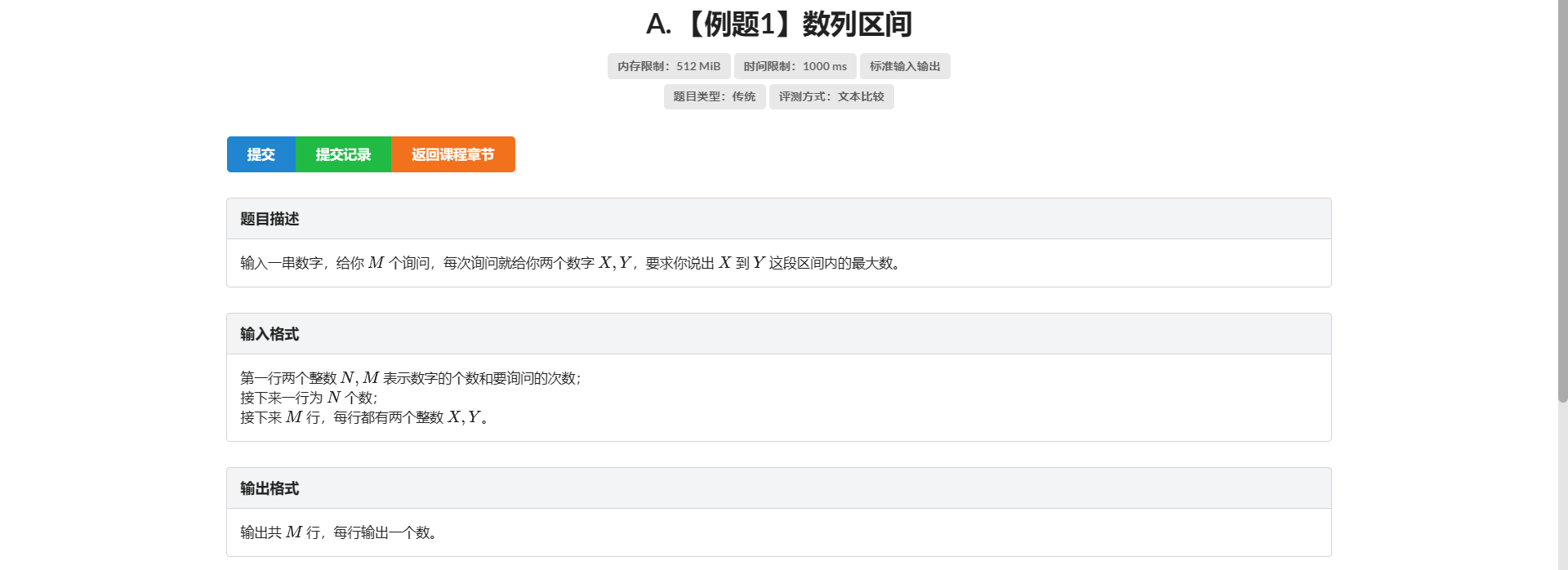
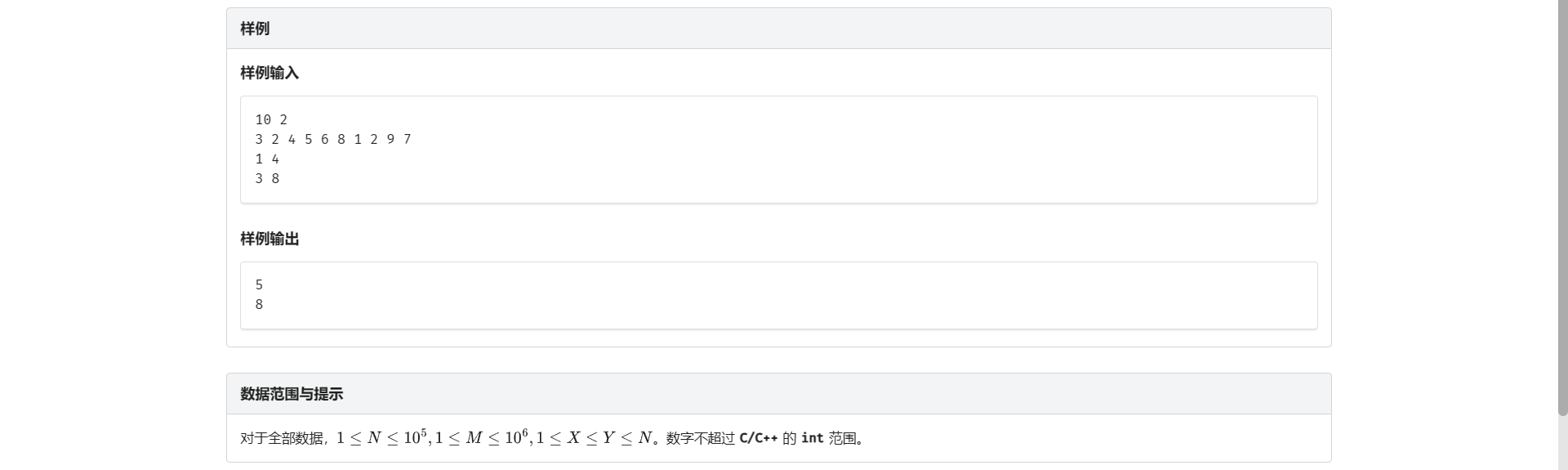
板子 详见P3865 ST表
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m;
const int N = 1e5 + 0721;
int a[N], rmq[N][21], Log[N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
Log[0] = -1;
for (int i = 1; i <= n; ++i) Log[i] = Log[i >> 1] + 1;
for (int i = 1; i <= n; ++i) rmq[i][0] = a[i];
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i + (1 << j) - 1 <= n; ++i)
rmq[i][j] = max(rmq[i][j - 1], rmq[i + (1 << (j - 1))][j - 1]);
}
for (int i = 1; i <= m; ++i) {
int l, r;
scanf("%d%d", &l, &r);
int x = r - l + 1;
int k = Log[x];
printf("%d\n", max(rmq[l][k], rmq[r - (1 << k) + 1][k]));
}
return 0;
}
B.静态区间
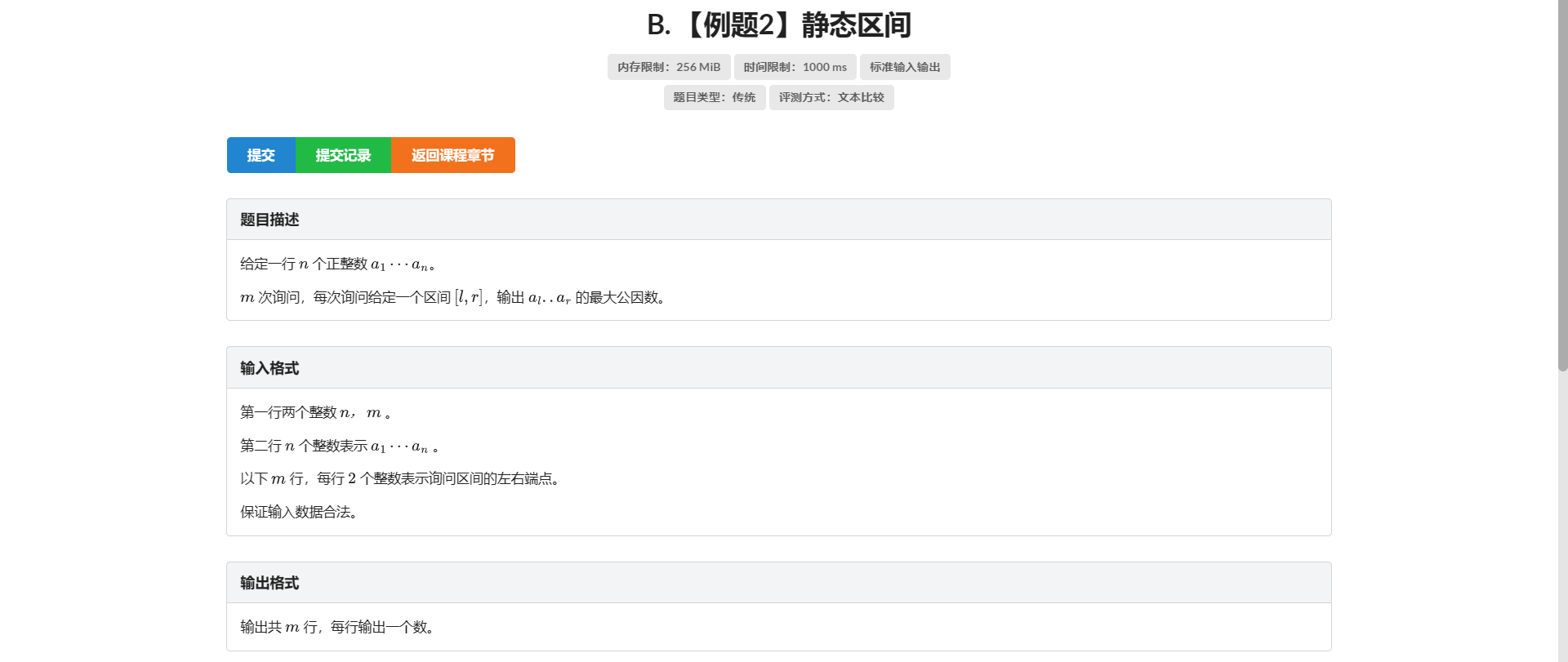
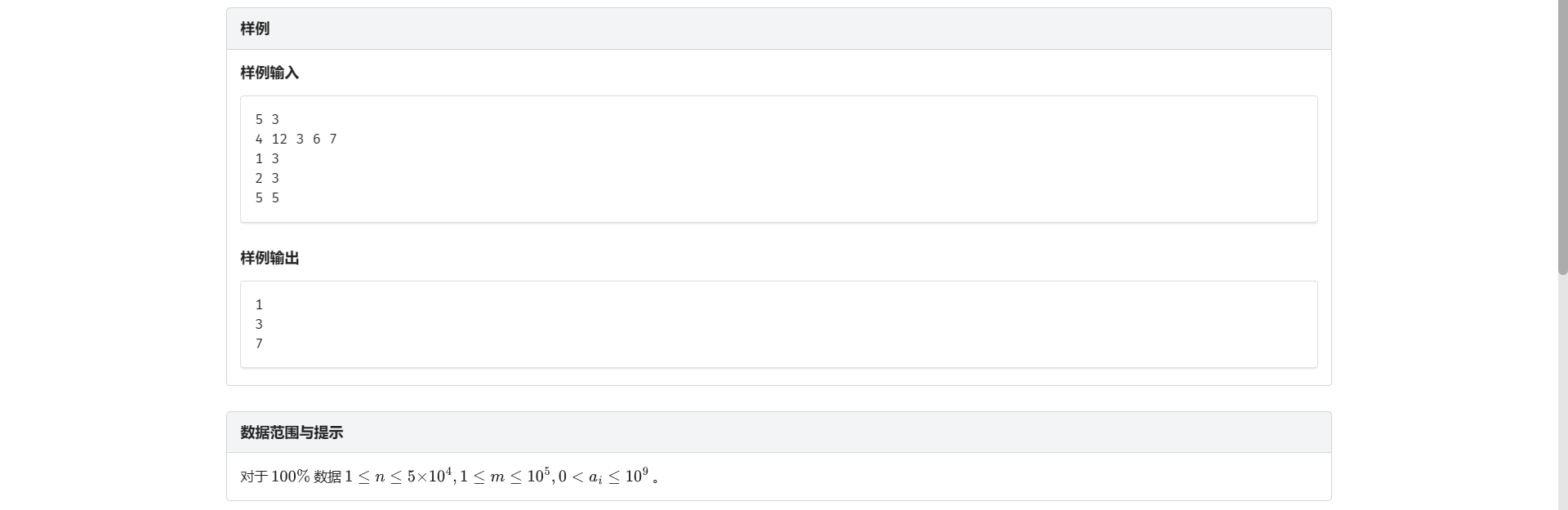
\(RMQ\) 的拓展应用
因为 \(RMQ\) 查询的时候实际上是查询两个中间有重叠区域的信息
所以实际上只要重叠不影响的信息就可以用 \(RMQ\) 查询
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
int rmq[N][21];
int a[N];
int Log[N];
int n, m;
int gcd(int x, int y) {
if (x < y)
swap(x, y);
if (y == 0)
return x;
else
return gcd(y, x % y);
}
inline int query(int l, int r) {
int k = Log[r - l + 1];
return gcd(rmq[l][k], rmq[r - (1 << k) + 1][k]);
}
int main() {
scanf("%d%d", &n, &m);
Log[0] = -1;
for (int i = 1; i <= n; ++i) Log[i] = Log[i >> 1] + 1;
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i) rmq[i][0] = a[i];
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i + (1 << j) - 1 <= n; ++i)
rmq[i][j] = gcd(rmq[i][j - 1], rmq[i + (1 << (j - 1))][j - 1]);
}
while (m--) {
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", query(l, r));
}
return 0;
}
C.与众不同
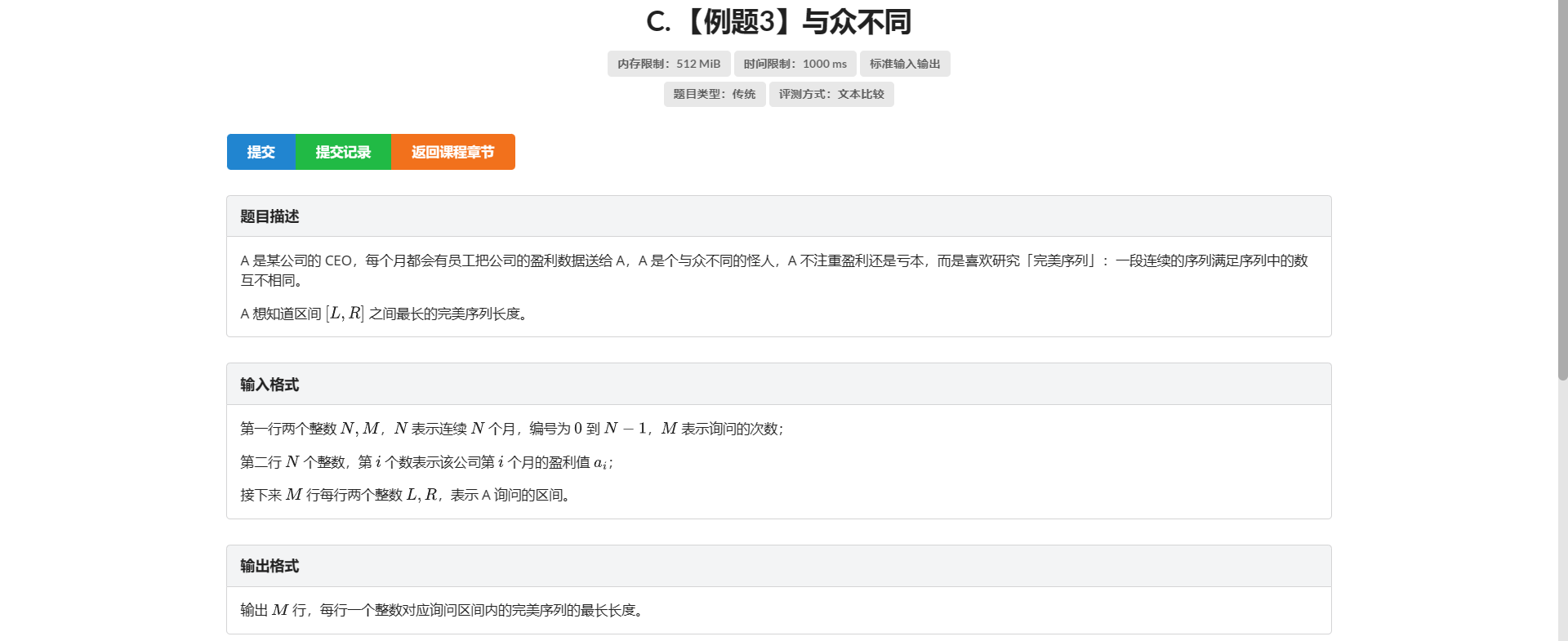
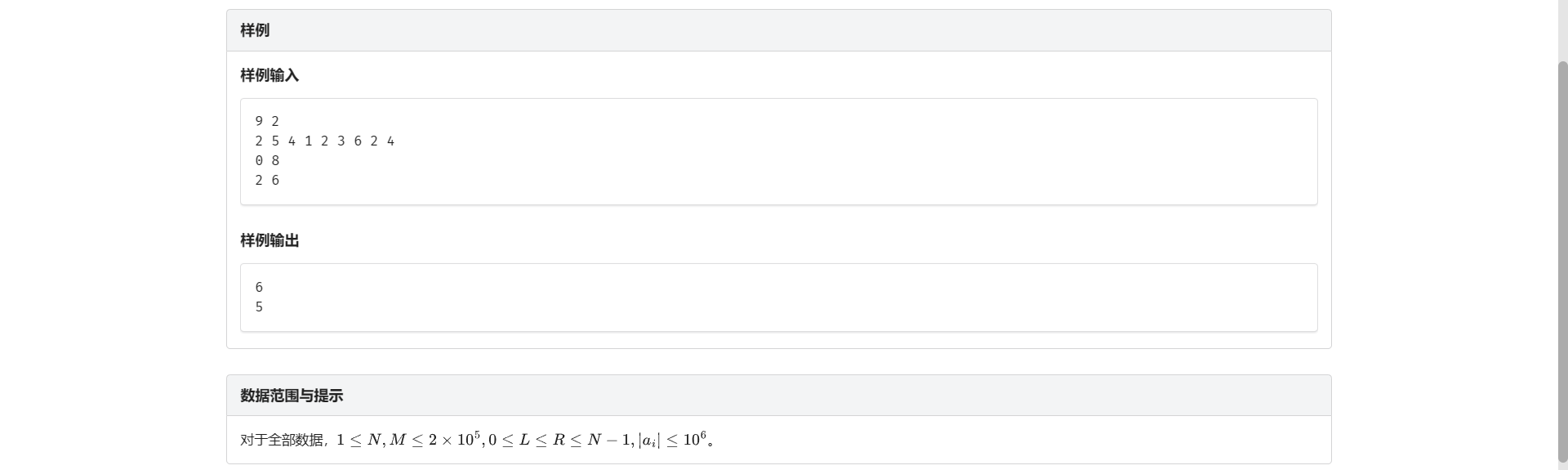
刚看这题口胡了一些类似于主席树二分离线线段树二分之类的做法
结果后来发现因为询问区间是 \(\left[l, r\right]\) 但是不一定答案区间左端点就是 \(l\) 所以就假了
非常的怄火
那不行就换个思路吧 我们注意到完美区间是一个连续区间
并且当 \(\left[l, r\right]\) 不是一个完美区间时 \(\left[l, r + 1\right]\) 一定不是一个完美区间
这不就可以双指针嘛!
我们设 \(f[i]\) 表示以 \(i\) 结尾最长的完美序列长度 然后双指针维护
我们接着考虑如何处理答案
因为不一定以 \(i\) 结尾的最长完美序列 左端点一定在 \(\left[l, r\right]\) 这个询问区间里
但是因为完美序列中间的任意一段都是完美区间 所以我们可以直接把它断掉
进一步思考 因为我们是双指针维护 所以当 \(r\) 右移时 \(l\) 一定单调不减
那我们就可以考虑二分 \(\left[l, r\right]\) 区间内第一个最长完美序列左端点在这个区间里的点 \(x\)
在它前面的 显然都要在 \(l\) 处断掉 所以最长的就是 \(\left[l, x - 1\right]\)
对于 \(\left[x, r\right]\) 这段区间 它们的最长完美序列都在这段区间里 所以可以直接用 \(ST\) 表查询 \(f[i]\) 的最大值
然后两个取个 \(max\) 即可
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 0721;
const int s6 = 1e6;
int lst[N], f[N], pre[N], a[N];
int Log[N];
int rmq[N][21];
int loc[N * 10];
int n, m;
inline int query(int l, int r) {
int k = Log[r - l + 1];
return max(rmq[l][k], rmq[r - (1 << k) + 1][k]);
}
int main() {
// freopen("1.txt", "r", stdin);
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i) {
lst[i] = loc[a[i] + s6];
loc[a[i] + s6] = i;
}
for (int i = 1; i <= n; ++i) {
pre[i] = max(pre[i - 1], lst[i] + 1);
f[i] = i - pre[i] + 1;
rmq[i][0] = f[i];
}
// for (int i = 1; i <= n; ++i) cout<<i<<" "<<pre[i]<<endl;
Log[0] = -1;
for (int i = 1; i <= n; ++i) Log[i] = Log[i >> 1] + 1;
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i + (1 << j) - 1 <= n; ++i) {
rmq[i][j] = max(rmq[i][j - 1], rmq[i + (1 << (j - 1))][j - 1]);
// cout<<i<<" "<<j<<" "<<rmq[i][j]<<endl;
}
}
while (m--) {
int l, r;
scanf("%d%d", &l, &r);
++l, ++r;
int ll = l, rr = r;
int mid, ans = l - 1;
while (l <= r) {
mid = (l + r) >> 1;
if (pre[mid] < ll) {
ans = mid;
l = mid + 1;
}
else
r = mid - 1;
}
int res = ans - ll + 1;
if (ans < rr)
res = max(query(ans + 1, rr), ans - ll + 1);
printf("%d\n",res);
}
return 0;
}
D.矩阵最值
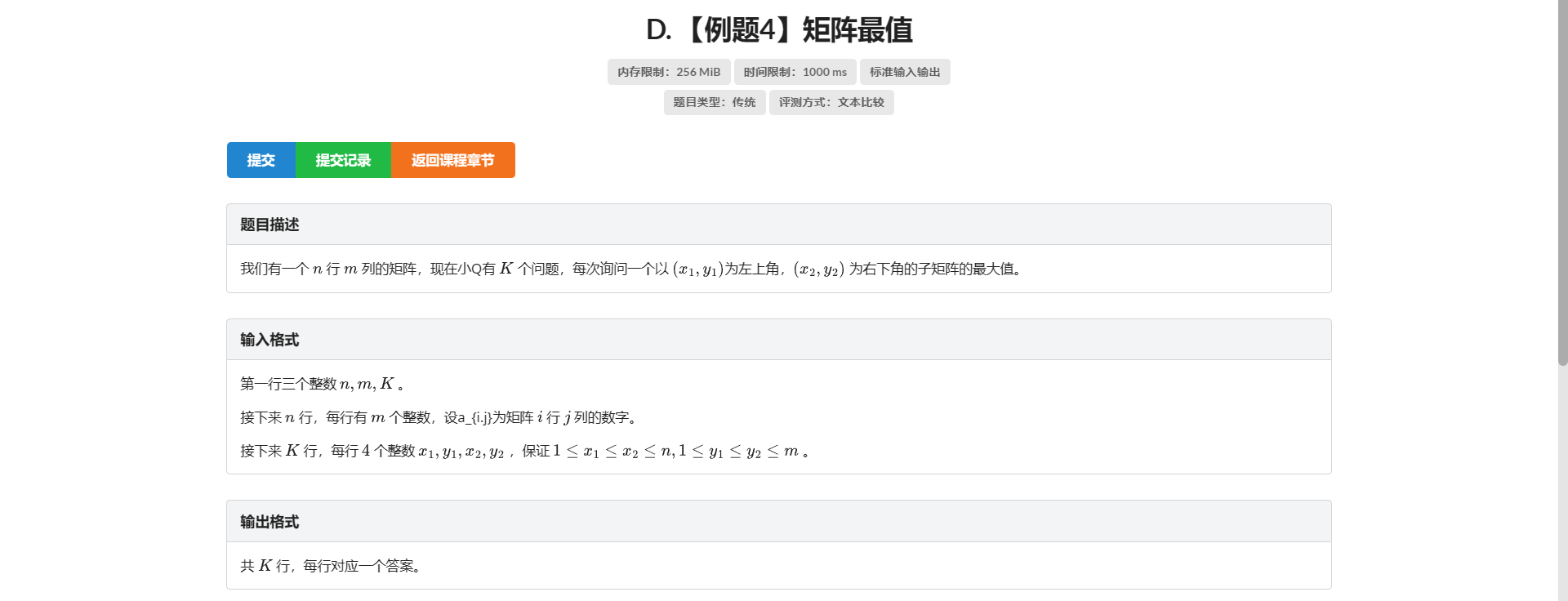
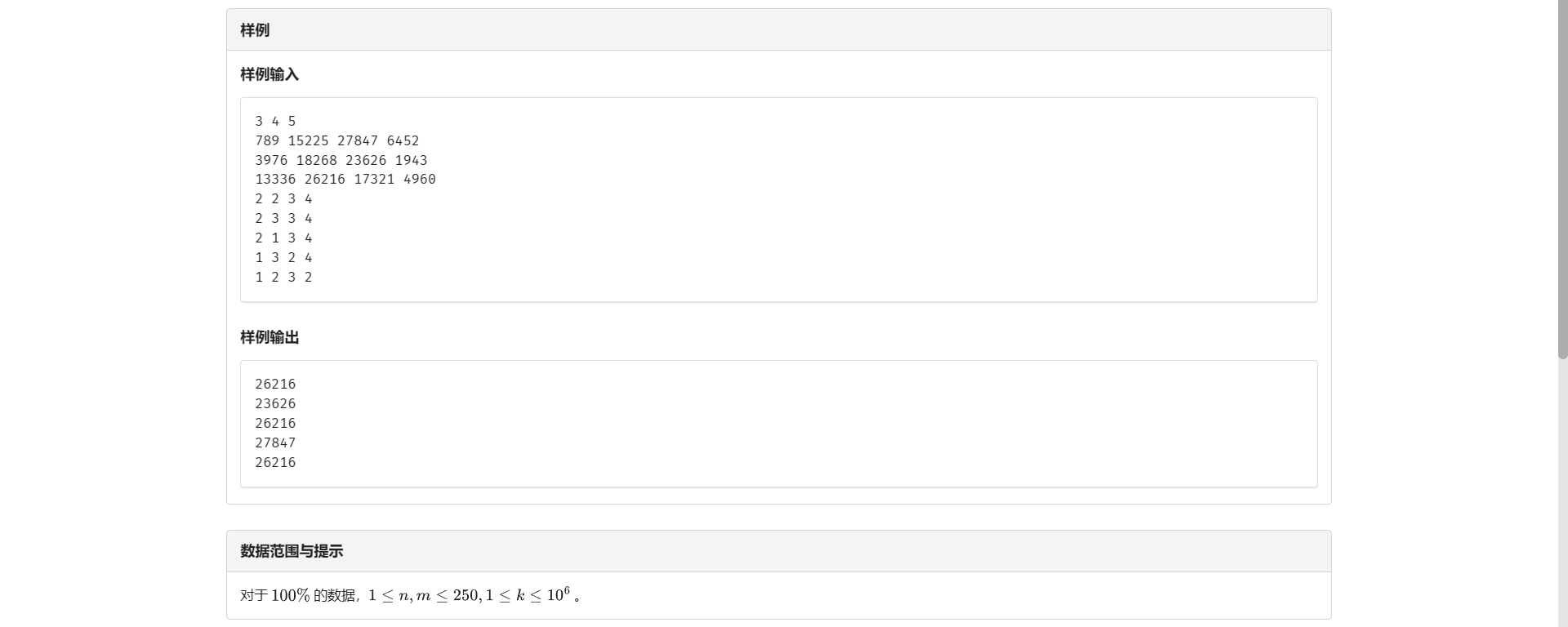
二维 \(ST\) 表 还是经典不看题解自己先想
还是考虑从一维转移到二维 就是先把每一行都按倍增预处理好
全整好之后再把处理好的每一行看成这一列的一个格 然后每一列按倍增预处理
查询的时候也是查询四个重叠矩形
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 300;
int f[N][N][11][11];
int Log[N];
int n, m, K;
inline int query(int x1, int y1, int x2, int y2) {
int k = Log[x2 - x1 + 1], h = Log[y2 - y1 + 1];
int max1 = max(f[x1][y1][k][h], f[x2 - (1 << k) + 1][y1][k][h]);
int max2 = max(f[x1][y2 - (1 << h) + 1][k][h], f[x2 - (1 << k) + 1][y2 - (1 << h) + 1][k][h]);
return max(max1, max2);
}
int main() {
scanf("%d%d%d", &n, &m, &K);
Log[0] = -1;
for (int i = 1; i <= max(n, m); ++i) Log[i] = Log[i >> 1] + 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) scanf("%d", &f[i][j][0][0]);
}
for (int k = 0; k <= Log[n]; ++k) {
for (int h = 0; h <= Log[m]; ++h) {
for (int i = 1; i + (1 << k) - 1 <= n; ++i) {
for (int j = 1; j + (1 << h) - 1 <= m; ++j) {
if (k == 0 && h == 0) continue;
if (k != 0)
f[i][j][k][h] = max(f[i][j][k - 1][h], f[i + (1 << (k - 1))][j][k - 1][h]);
else
f[i][j][k][h] = max(f[i][j][k][h - 1], f[i][j + (1 << (h - 1))][k][h - 1]);
}
}
}
}
while (K--) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n",query(x1, y1, x2, y2));
}
return 0;
}
E.接水问题
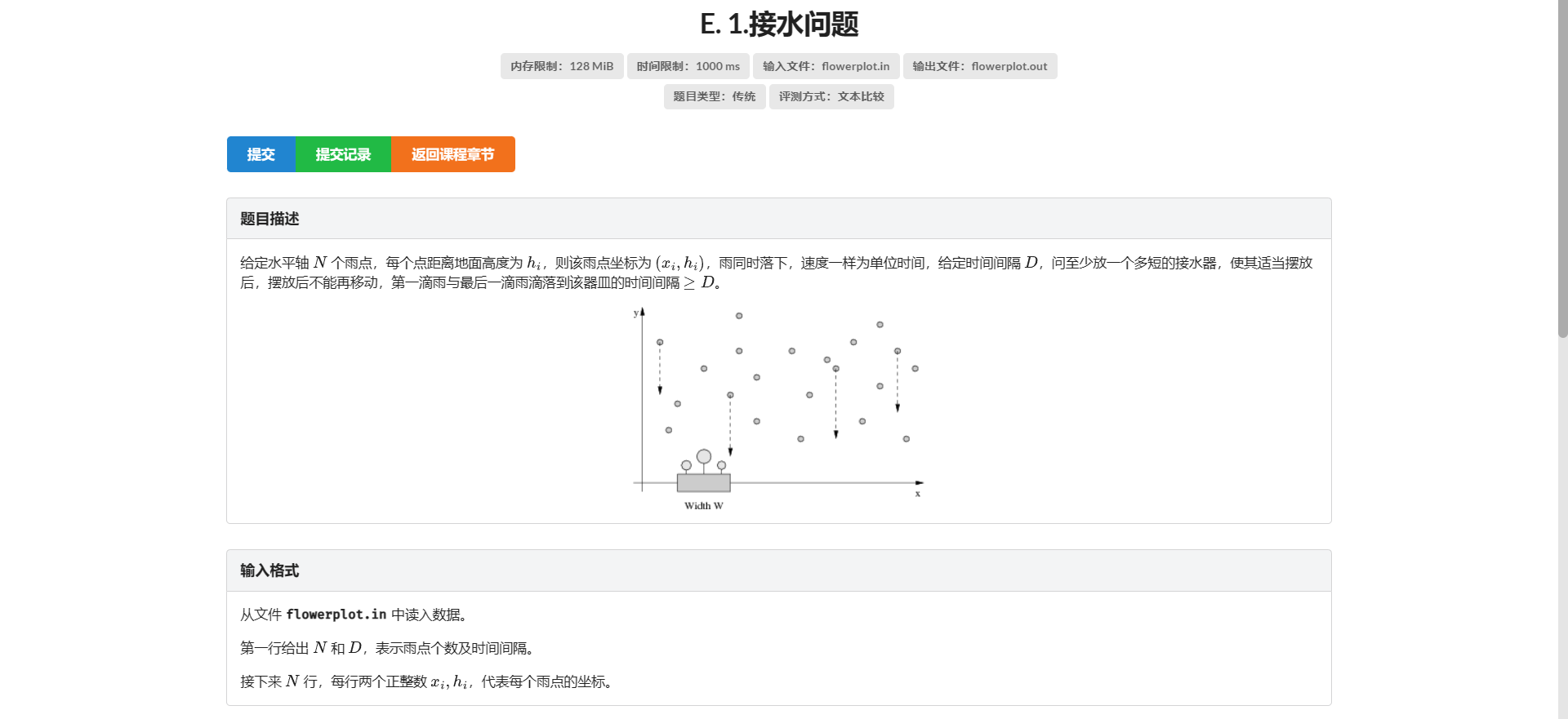
首先这个看上去就很可以二分答案
我们考虑二分这个水槽的长度 然后暴力枚举区间起点来 \(check\)
那么实际上第一滴水和最后一滴水的间隔时间就是区间 \(\max\) 减区间 \(\min\) 这个东西就可以用 ST 表来查
这题的区间长度竟然是 \(r - l\) 而不是 \(r - l + 1\) /fn
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 1e6 + 0721;
const int inf = 0x7fffffff;
int maxn[N][21], minn[N][21];
int b[N];
bool vis[N];
int n, k, d;
struct node {
int x, h;
} a[N];
void init() {
for (int i = 1; i <= k; ++i) minn[i][0] = inf;
for (int i = 1; i <= n; ++i) {
minn[a[i].x][0] = min(minn[a[i].x][0], a[i].h);
maxn[a[i].x][0] = max(maxn[a[i].x][0], a[i].h);
}
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i + (1 << j) - 1 <= k; ++i) {
maxn[i][j] = max(maxn[i][j - 1], maxn[i + (1 << (j - 1))][j - 1]);
minn[i][j] = min(minn[i][j - 1], minn[i + (1 << (j - 1))][j - 1]);
}
}
}
int qmax(int l, int r) {
int tmp = log2(r - l + 1);
return max(maxn[l][tmp], maxn[r - (1 << tmp) + 1][tmp]);
}
int qmin(int l, int r) {
int tmp = log2(r - l + 1);
return min(minn[l][tmp], minn[r - (1 << tmp) + 1][tmp]);
}
bool check(int len) {
int ret = 0;
for (int i = 1; i + len <= k; ++i) {
int r = i + len;
ret = max(ret, qmax(i, r) - qmin(i, r));
}
return ret >= d;
}
int binary_search() {
int l = 1, r = k;
int mid, ans = -1;
while (l <= r) {
mid = (l + r) >> 1;
if (check(mid)) {
ans = mid;
r = mid - 1;
} else
l = mid + 1;
}
return ans;
}
void main() {
freopen("flowerplot.in", "r", stdin);
freopen("flowerplot.out", "w", stdout);
scanf("%d%d", &n, &d);
for (int i = 1; i <= n; ++i) {
scanf("%d%d", &a[i].x, &a[i].h);
k = max(k, a[i].x);
}
init();
printf("%d\n", binary_search());
}
}
int main() {
steven24::main();
return 0;
}
/*
4 5
6 3
2 4
4 10
12 15
*/
F.方阵问题
第一次做题被卡空间
一眼二维 ST 元素和直接二维差分秒了
一算空间 炸了
如果对每一行开 ST 然后询问的时候把每行都暴力查一遍 复杂度就是 \(4 \times 10 ^ 8\)
感谢 bot 帮忙卡常 直接暴力艹过去了(主要是把倍增数组开在最前面缩短寻址时间)
点击查看代码
#include <bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
namespace steven24 {
const int N = 801;
const int inf = 0x7fffffff;
int maxn[10][N][N];
int minn[10][N][N];
int d[N][N];
char opt[4];
int n, m;
inline int read() {
int xr = 0;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') ;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr;
}
void init() {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) d[i][j] = d[i][j - 1] + maxn[0][i][j];
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) d[i][j] += d[i - 1][j];
}
for (int i = 1; i <= n; ++i)
for (int k = 1; k <= 9; ++k)
for (int j = 1; j + (1 << k) - 1 <= m; ++j)
maxn[k][i][j] = max(maxn[k - 1][i][j], maxn[k - 1][i][j + (1 << (k - 1))]),
minn[k][i][j] = min(minn[k - 1][i][j], minn[k - 1][i][j + (1 << (k - 1))]);
}
inline int query_sum(int x1, int y1, int x2, int y2) {
return d[x2][y2] - d[x2][y1 - 1] - d[x1 - 1][y2] + d[x1 - 1][y1 - 1];
}
inline int query_max(int x, int l, int r) {
int k = __lg(r - l + 1);
return max(maxn[k][x][l], maxn[k][x][r - (1 << k) + 1]);
}
inline int query_min(int x, int l, int r) {
int k = __lg(r - l + 1);
return min(minn[k][x][l], minn[k][x][r - (1 << k) + 1]);
}
void main() {
n = read(), m = read();
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
minn[0][i][j] = maxn[0][i][j] = read();
init();
int T = read();
while (T--) {
scanf("%s", opt);
int x1, x2, y1, y2;
x1 = read(), y1 = read(), x2 = read(), y2 = read();
++x1, ++y1, ++x2, ++y2;
if (opt[1] == 'U') printf("%d\n", query_sum(x1, y1, x2, y2));
else if (opt[1] == 'A') {
int ans = 0;
for (int i = x1; i <= x2; ++i) ans = max(ans, query_max(i, y1, y2));
printf("%d\n", ans);
} else {
int ans = inf;
for (int i = x1; i <= x2; ++i) ans = min(ans, query_min(i, y1, y2));
printf("%d\n", ans);
}
}
}
}
int main() {
steven24::main();
return 0;
}
/*
3 3
1 2 3
4 5 6
7 8 9
3
SUM 0 0 1 1
MAX 0 0 2 2
MIN 0 1 1 1
*/
G.降雨量
竟然能一次 AC 这题 感动
本质就是多情况分讨 看着就很不想写 这一章最后写的题 只能说没写 CSP-S2022 T2 来还债了
主要把思路捋清
首先根据题目分析 为方便起见 我们设 \(Z\) 表示 \(X + 1\) 到 \(Y - 1\) 这段年份的降雨量最大值
我们可以得到两个信息:
- \(X \le Y\)
- \(Z < X\)
把这两个信息综合一下 我们还可以得到 \(Z < Y\)
这样我们就得到了这三个量之间两两的关系
知道这个关系可以让思路清晰不少
我们设 \(flag1/2/3\) 分别表示这三条关系的真假 它们的初值都是 \(-1\) 表示真假未知
-
如果 \(X\) 与 \(Y\) 的降水量都已知并且 \(X \le Y\) 则 \(flag1 = 1\)
-
如果 \(X\) 与 \(Y\) 的降水量都已知并且 \(X > Y\) 则 \(flag1 = 0\)
-
如果 \(\left[X, Y\right]\) 这段的降水量都已知 \(X\) 的降水量已知 并且 \(X > Z\) 则 \(flag2 = 1\)
-
如果 \(X\) 的降水量已知 并且 \(X \le Z\) 则 \(flag2 = 0\)
-
如果 \(\left[X, Y\right]\) 这段的降水量都已知 \(Y\) 的降水量已知 并且 \(Y > Z\) 则 \(flag3 = 1\)
-
如果 \(Y\) 的降水量已知 并且 \(Y \le Z\) 则 \(flag3 = 0\)
那么如果最后 \(flag1/2/3\) 全为 \(1\) 就是 true
如果 \(flag1/2/3\) 有一个为 \(0\) 就是 false
否则 就是 maybe
我们发现 \(Z\) 就是区间最大值 拿 ST 表维护即可
对于判断某段区间降水量是否已知 我们参考 ST 表 用 \(exist_{i, j}\) 表示 \(\left[i, i + 2^j - 1\right]\) 这段区间内的降水量是否都已知
那么转移的时候就是左右两半的与
并且 \(X\) 和 \(Y\) 的降水量不一定已知 所以要用二分查找编号
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 5e4 + 0721;
int maxn[21][N];
bool exist[21][N];
int Log[N];
int yy[N];
int n, m;
struct node {
int y, r;
} a[N];
void init() {
for (int i = 2; i <= n; ++i) Log[i] = Log[i >> 1] + 1;
for (int i = 1; i <= n; ++i) maxn[0][i] = a[i].r;
for (int j = 1; j <= Log[n]; ++j) {
for (int i = 1; i + (1 << j) - 1 <= n; ++i) maxn[j][i] = max(maxn[j - 1][i], maxn[j - 1][i + (1 << (j - 1))]);
}
for (int i = 1; i < n; ++i) {
if (a[i + 1].y == a[i].y + 1) exist[1][i] = 1;
else exist[1][i] = 0;
}
for (int j = 2; j <= Log[n]; ++j) {
for (int i = 1; i + (1 << j) - 1 <= n; ++i) exist[j][i] = (exist[j - 1][i] & exist[j - 1][i + (1 << (j - 1))]);
}
}
int query_max(int l, int r) {
if (l > r) return 0;
int k = Log[r - l + 1];
return max(maxn[k][l], maxn[k][r - (1 << k) + 1]);
}
bool query_exist(int l, int r) {
int k = Log[r - l + 1];
return (exist[k][l] & exist[k][r - (1 << k) + 1]);
}
void main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d%d", &a[i].y, &a[i].r);
yy[i] = a[i].y;
}
init();
scanf("%d", &m);
while (m--) {
int x, y;
scanf("%d%d", &x, &y);
int flag1 = -1, flag2 = -1, flag3 = -1;
bool existz;
int locx = lower_bound(yy + 1, yy + 1 + n, x) - yy - 1;
int locy = lower_bound(yy + 1, yy + 1 + n, y) - yy;
if (a[locx + 1].y == x) ++locx;
if (a[locx].y == x && a[locy].y == y) existz = query_exist(locx, locy);
else if (a[locx].y == x) existz = query_exist(locx, locy - 1);
else if (a[locy].y == y) existz = query_exist(locx + 1, locy);
else existz = query_exist(locx + 1, locy - 1);
if (a[locx].y == x && a[locy].y == y && a[locx].r >= a[locy].r) flag1 = 1;
else if (a[locx].y == x && a[locy].y == y && a[locx].r < a[locy].r) flag1 = 0;
if (existz && a[locx].y == x && a[locx].r > query_max(locx + 1, locy - 1)) flag2 = 1;
else if (a[locx].y == x && a[locx].r <= query_max(locx + 1, locy - 1)) flag2 = 0;
if (existz && a[locy].y == y && a[locy].r > query_max(locx + 1, locy - 1)) flag3 = 1;
else if (a[locy].y == y && a[locy].r <= query_max(locx + 1, locy - 1)) flag3 = 0;
if (flag1 == 1 && flag2 == 1 && flag3 == 1) printf("true\n");
else if (flag1 == 0 || flag2 == 0 || flag3 == 0) printf("false\n");
else printf("maybe\n");
}
}
}
int main() {
steven24::main();
return 0;
}
/*
6
2002 4920
2003 5901
2004 2832
2005 3890
2007 5609
2008 3024
5
2002 2005
2003 2005
2002 2007
2003 2007
2005 2008
*/
H.超级钢琴
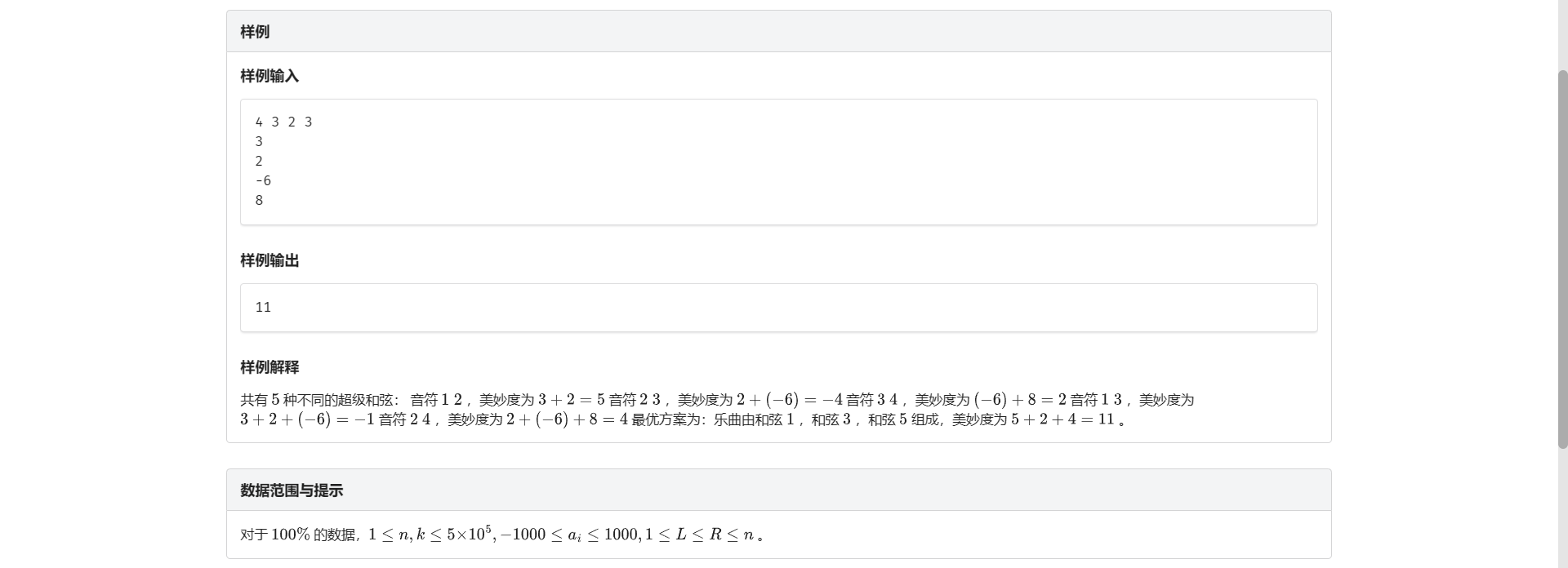
八个月了 怎么一点长进没有 玉玉了
首先把这个区间和转化成前缀和差分
然后考虑枚举选取区间的左端点 \(i\) 那么右端点就是在 \(\left[i + l - 1, i + r - 1\right]\) 这段区间内前缀和最大的点 这个东西可以用 ST 表查
然后把这玩意推进堆
每次弹出的时候就把它换成这段区间的次大值、次次大值...推进去
到这就不会了 以下是正解剩余部分内容
设当前区间前缀和最大的点的位置是 \(p\) 那么次大值要么是 \(\left[i + l - 1, p - 1\right]\) 的最大值要么是 \(\left[p + 1, i + r - 1\right]\) 的最大值 直接把两个都放进堆里就好了
更具体地 我们设三元组 \((i, l, r)\) 表示左端点在 \(i\) 右端点在 \(\left[i + l - 1, i + r - 1\right]\) 这段区间的最大子段和
我们在记录一下这个取到这个最大子段和对应的位置 假设这个位置为 \(i + p - 1\)
那么每次选取这段的时候就把 \((i, l, p - 1)\) 和 \((i, p + 1, r)\) 再推进堆里即可
代码是八个月前写的 可能有些乱见谅
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 500721;
int c[N], rmq[N][21], num[N][21];
int n, k, l, r;
ll ans;
struct node {
int st, enl, enr, en, val;
friend bool operator<(node x, node y) { return x.val < y.val; }
};
priority_queue<node, vector<node>, less<node> > q;
int qwz(int le, int ri) {
int j = log2(ri - le + 1);
if (rmq[le][j] < rmq[ri + 1 - (1 << j)][j])
return num[ri + 1 - (1 << j)][j];
else
return num[le][j];
}
int main() {
scanf("%d%d%d%d", &n, &k, &l, &r);
for (int i = 1; i <= n; ++i) {
int x;
scanf("%d", &x);
c[i] = c[i - 1] + x;
rmq[i][0] = c[i];
num[i][0] = i;
}
for (int j = 1; j <= 20; ++j) {
for (int i = 1; i + (1 << j) - 1 <= n; ++i) {
if (rmq[i][j - 1] < rmq[i + (1 << (j - 1))][j - 1]) {
rmq[i][j] = rmq[i + (1 << (j - 1))][j - 1];
num[i][j] = num[i + (1 << (j - 1))][j - 1];
} else {
rmq[i][j] = rmq[i][j - 1];
num[i][j] = num[i][j - 1];
}
}
}
for (int i = 1; i + l - 1 <= n; ++i) {
int zuo = i + l - 1;
int you = min(i + r - 1, n);
q.push((node){ i, zuo, you, qwz(zuo, you), c[qwz(zuo, you)] - c[i - 1] });
// cout<<i<<" "<<zuo<<" "<<you<<" "<<qwz(zuo,you)<<" "<<c[qwz(zuo,you)]-c[i-1]<<endl;
}
while (k--) {
int sta = q.top().st, lef = q.top().enl, righ = q.top().enr, wei = q.top().en, v = q.top().val;
q.pop();
ans += v;
if (lef < wei)
q.push((node){ sta, lef, wei - 1, qwz(lef, wei - 1), c[qwz(lef, wei - 1)] - c[sta - 1] });
if (wei < righ)
q.push((node){ sta, wei + 1, righ, qwz(wei + 1, righ), c[qwz(wei + 1, righ)] - c[sta - 1] });
}
printf("%lld", ans);
return 0;
}
I.二叉查找树
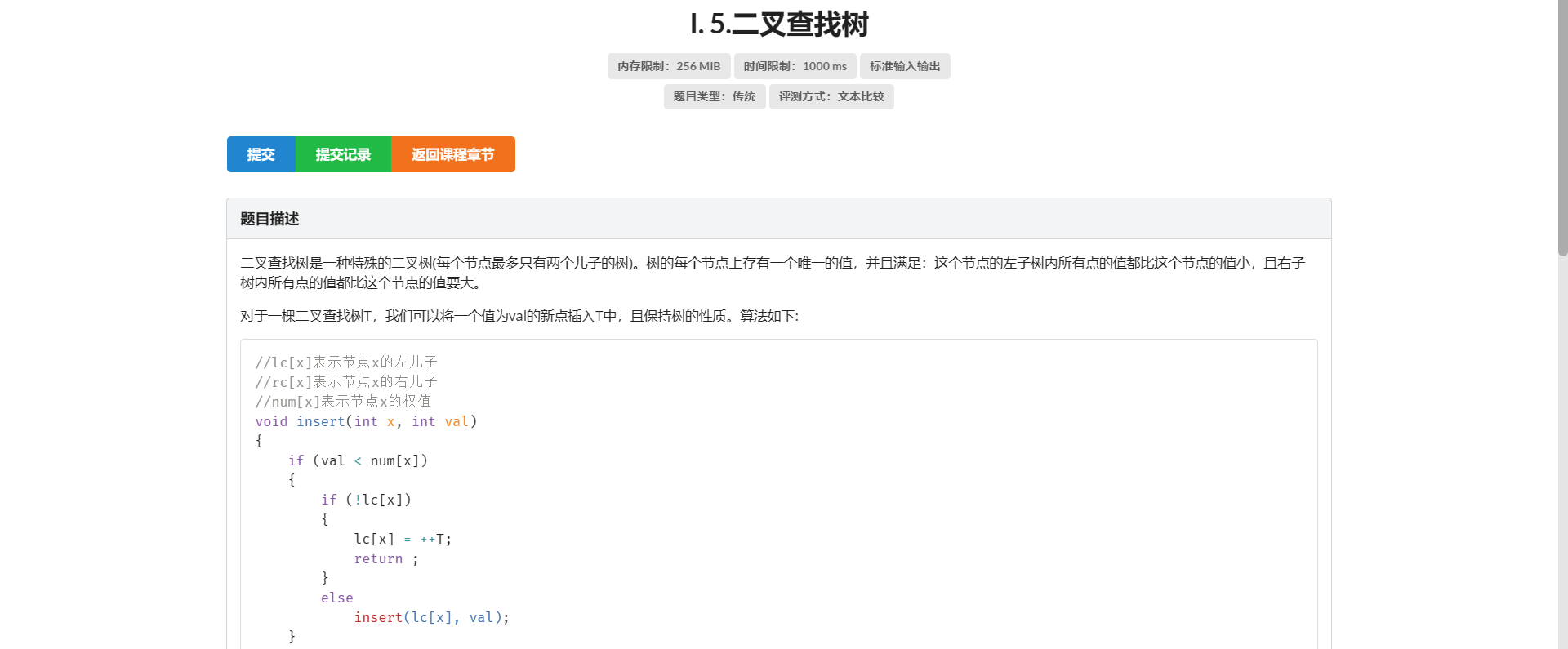
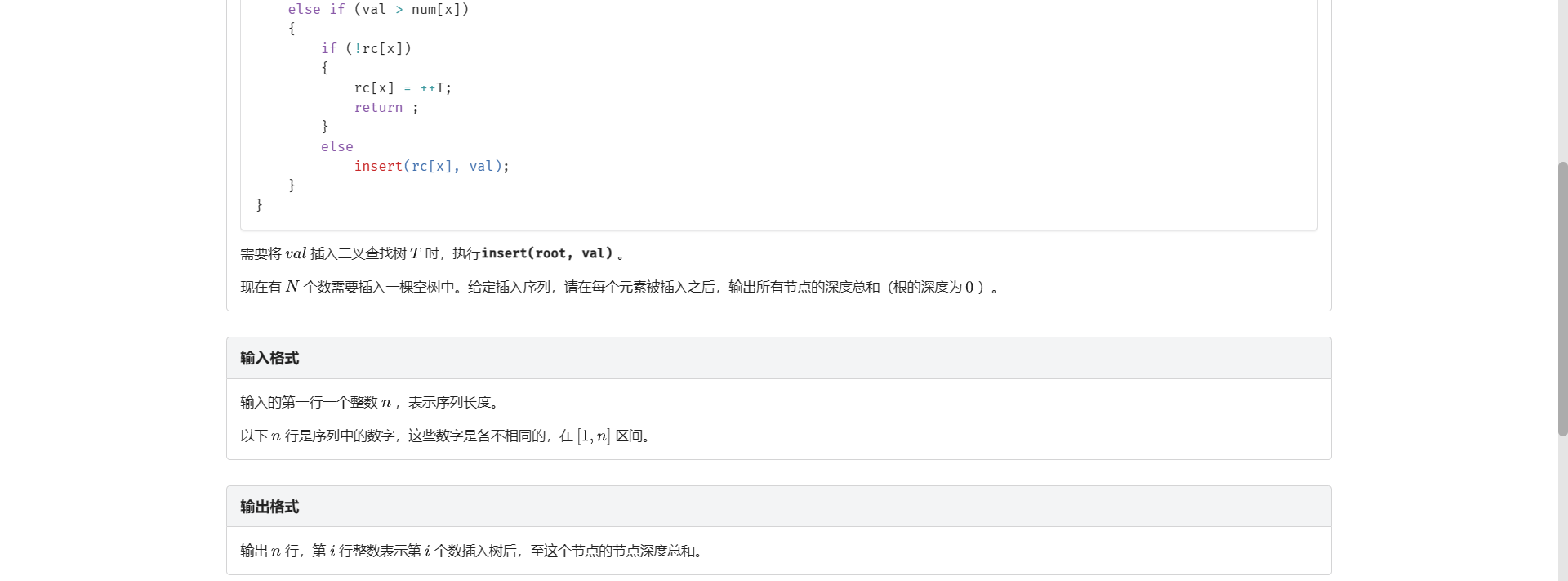
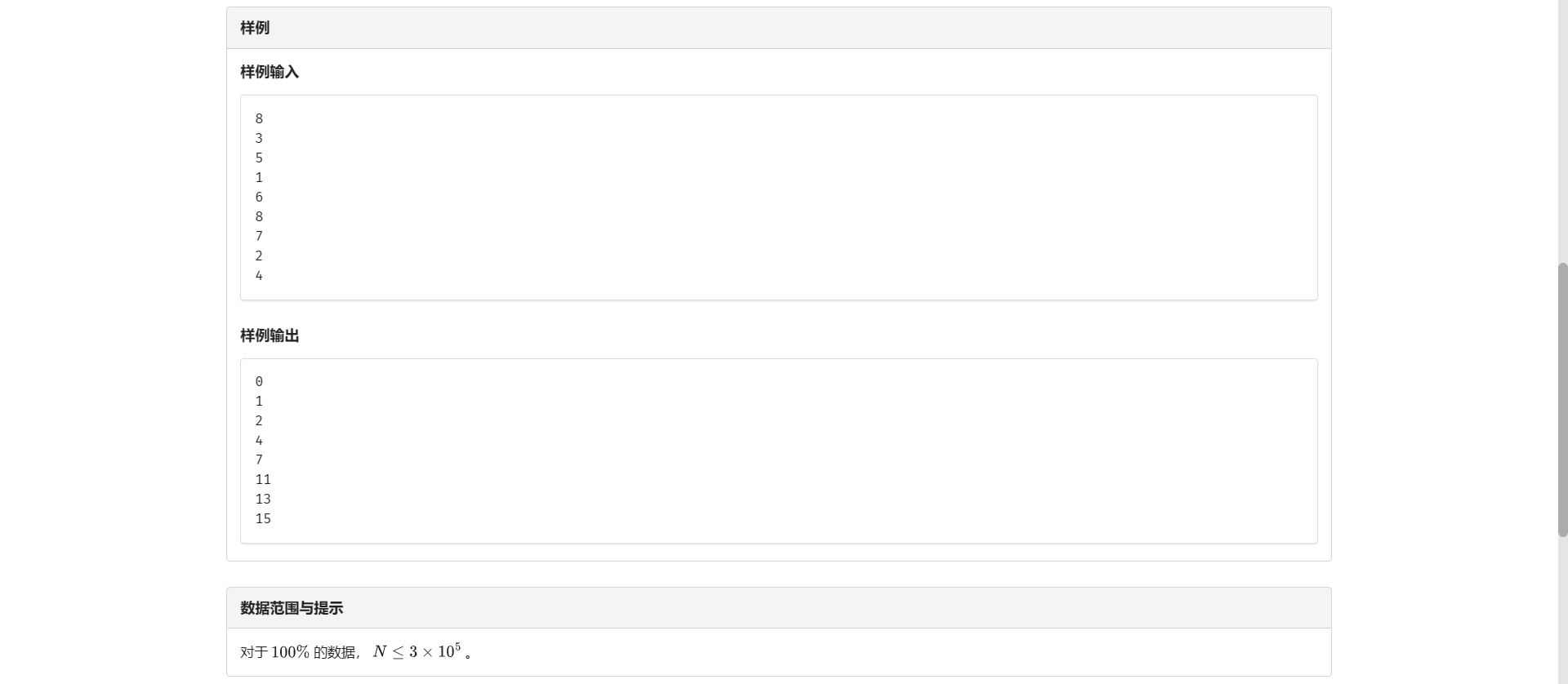
没用到 ST 表(
很直接的一个想法就是根据它的代码暴力插入并且记录父亲
这样在随机数据下确实期望复杂度是 \(\text{O} (n \log n)\) 的 但是极端数据下会让整棵 BST 变成一条链 复杂度就退化到了 \(\text{O}(n^2)\) 不然也不会有平衡树这种东西
这里讲下我的思路
因为我们每次只需要找到当前这个点插入时应该连在哪个点上
而被连的点一定是左右儿子至少有一个为空的点
并且根据直觉 最后一层的能被连的点只会有一个
并且最后一层的每个点能管辖的点的区间应该是连续的
所以 \(\left[1, n\right]\) 这段区间应该是连续的一段一段被最后一层的不同点所管辖
于是想到开一个数组 其中 \(a_i\) 表示如果将值为 \(i\) 的点插当前的 BST 中 它的父亲节点就是 \(a_i\)
结合样例讲述一下具体过程
首先第一个数一定是根节点 此时任何数再插一定都要接到它下面 所以当前 \(a\) 数组就是
3 3 3 3 3 3 3 3
然后我们把 \(5\) 插入 那么此时 \(\left[4, 8\right]\) 的数插入一定就是接 \(5\)
对于 \(\left[1, 3\right]\) 的数 还是接 \(3\) (因为还有左儿子可以连)
3 3 3 5 5 5 5 5
然后插入 \(1\) \(1\) 要连 \(3\) 所有 \(\left[1, 2\right]\) 的数此时都要连 \(1\)
1 1 3 5 5 5 5 5
插入 \(6\) 接在 \(5\) 后面 所有 \(\left[6, 8\right]\) 的数此时都要连 \(6\)
1 1 3 5 5 6 6 6
持续此过程
1 1 3 5 5 6 8 8
1 1 3 5 5 6 7 8
1 2 3 5 5 6 7 8
1 2 3 4 5 6 7 8
至此 插入完成
我们发现 每次插入一个点 实际它管辖的区间就是:
- 如果它 \(<\) 它父亲 就是它父亲原来管辖的左端点到它父亲 -1
- 如果它 \(>\) 它父亲 就是它父亲 +1 到它父亲原来管辖的右端点
显然我们直接维护出每个点管辖的左右端点和该点的深度 那么维护 \(a\) 数组实际上就是一个区间赋值 直接用线段树维护即可 好像也可以用珂朵莉树(?
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define ls (k << 1)
#define rs (k << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
namespace steven24 {
const int N = 3e5 + 0721;
int a[N], dep[N];
int lv[N], rv[N];
int n;
ll ans;
struct segment_tree {
int lazy[N << 2];
inline void pushdown(int k) {
lazy[ls] = lazy[k];
lazy[rs] = lazy[k];
lazy[k] = -1;
}
void modify(int k, int l, int r, int u, int v, int val) {
if (u <= l && v >= r) {
lazy[k] = val;
return;
}
if (lazy[k] != -1) pushdown(k);
if (u <= mid) modify(ls, l, mid, u, v, val);
if (v > mid) modify(rs, mid + 1, r, u, v, val);
}
int query(int k, int l, int r, int loc) {
if (l == r) {
return lazy[k];
}
if (lazy[k] != -1) pushdown(k);
if (loc <= mid) return query(ls, l, mid, loc);
else return query(rs, mid + 1, r, loc);
}
} seg;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 1) + (xr << 3) + (cr ^ 48), cr = getchar();
return xr * F;
}
void main() {
n = read();
for (int i = 1; i <= n; ++i) a[i] = read();
memset(seg.lazy, -1, sizeof seg.lazy);
dep[a[1]] = 0;
seg.modify(1, 1, n, 1, n, a[1]);
lv[a[1]] = 1;
rv[a[1]] = n;
printf("%lld\n", ans);
for (int i = 2; i <= n; ++i) {
int val = seg.query(1, 1, n, a[i]);
if (val == a[i]) continue;
dep[a[i]] = dep[val] + 1;
ans += dep[a[i]];
printf("%lld\n", ans);
if (val > a[i] && lv[val] <= val - 1) {
seg.modify(1, 1, n, lv[val], val - 1, a[i]);
lv[a[i]] = lv[val];
rv[a[i]] = val - 1;
}
else if (val < a[i] && rv[val] >= val + 1) {
seg.modify(1, 1, n, val + 1, rv[val], a[i]);
lv[a[i]] = val + 1;
rv[a[i]] = rv[val];
}
}
}
}
int main() {
steven24::main();
return 0;
}
/*
8
3
5
1
6
8
7
2
4
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号