YBTOJ 4.2树状数组
A.单点修改区间查询
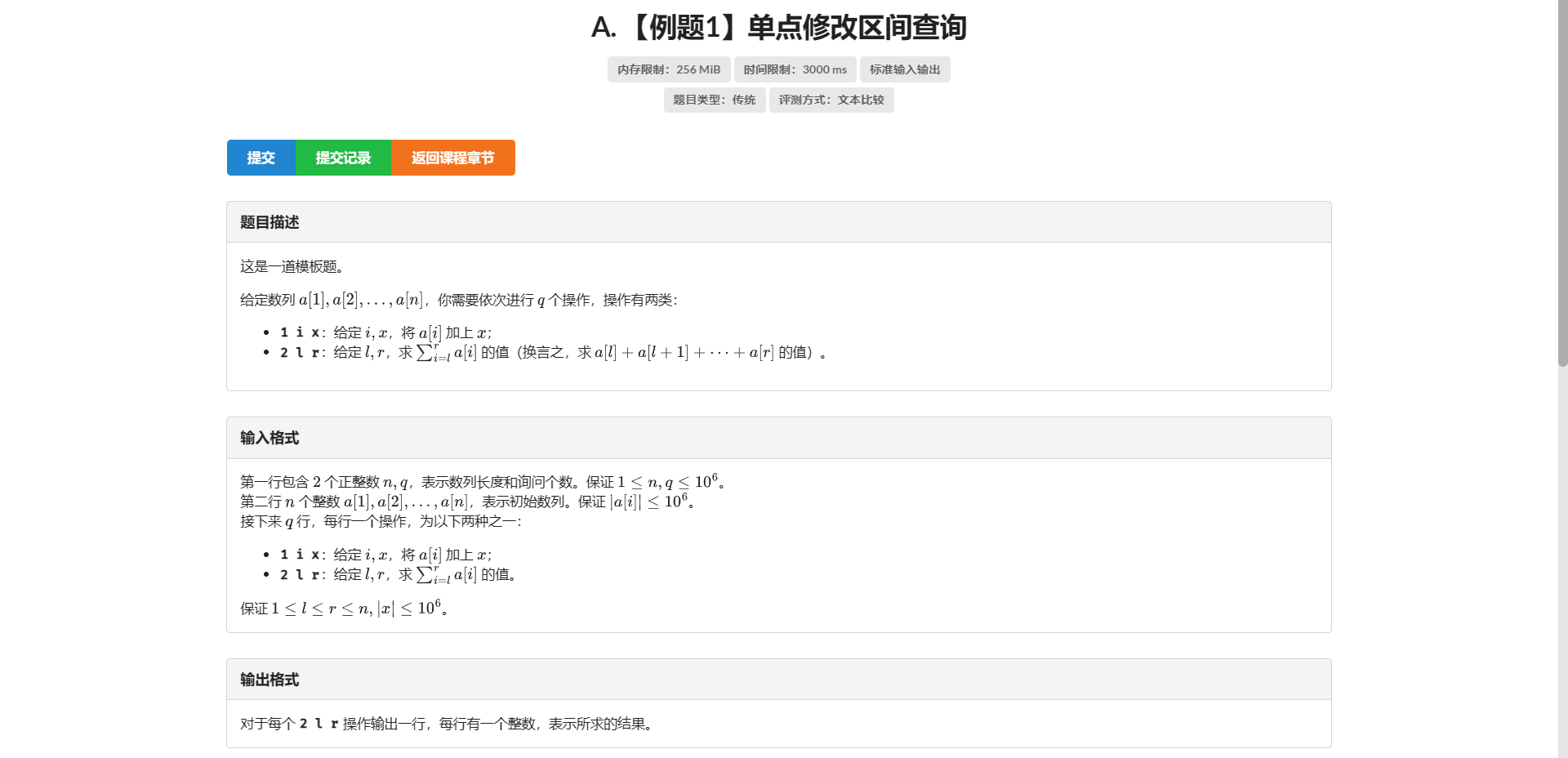
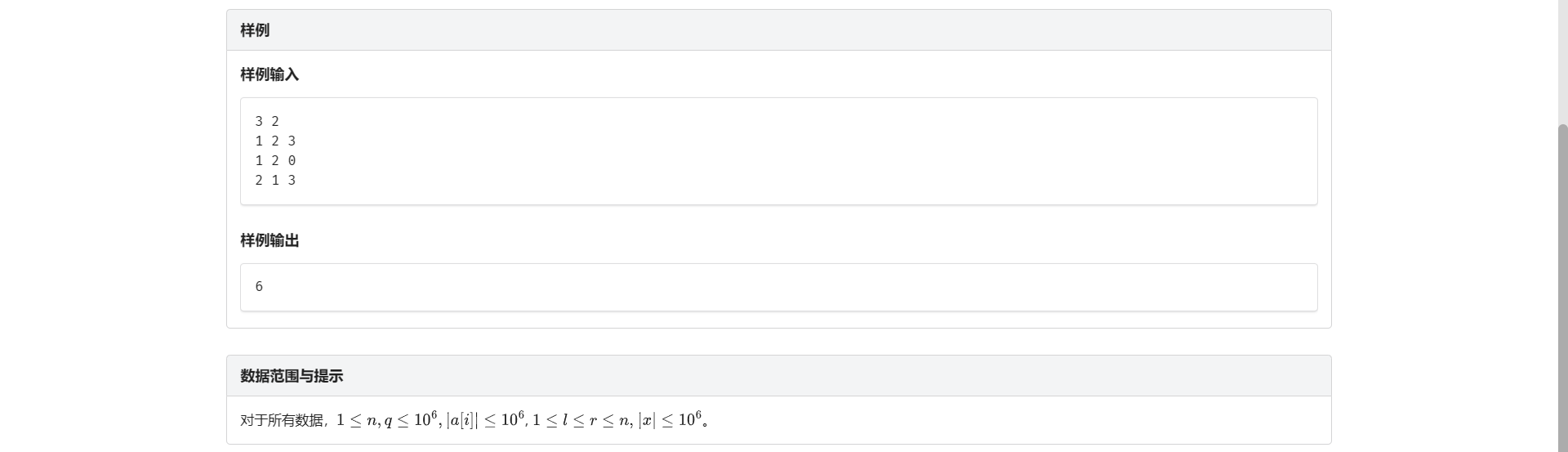
板子
点击查看代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 0721;
int c[N];
int n, m;
int lowbit(int x) { return x & (-x); }
void xg(int i, int v) {
while (i <= n) {
c[i] += v;
i += lowbit(i);
}
}
int ques(int x) {
int val = 0;
while (x) {
val += c[x];
x -= lowbit(x);
}
return val;
}
signed main() {
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; ++i) {
int x;
scanf("%lld", &x);
xg(i, x);
}
for (int i = 1; i <= m; ++i) {
int shu, x, y;
scanf("%lld%lld%lld", &shu, &x, &y);
if (shu == 1) {
xg(x, y);
} else {
printf("%lld\n", ques(y) - ques(x - 1));
}
}
return 0;
}
B.逆序对
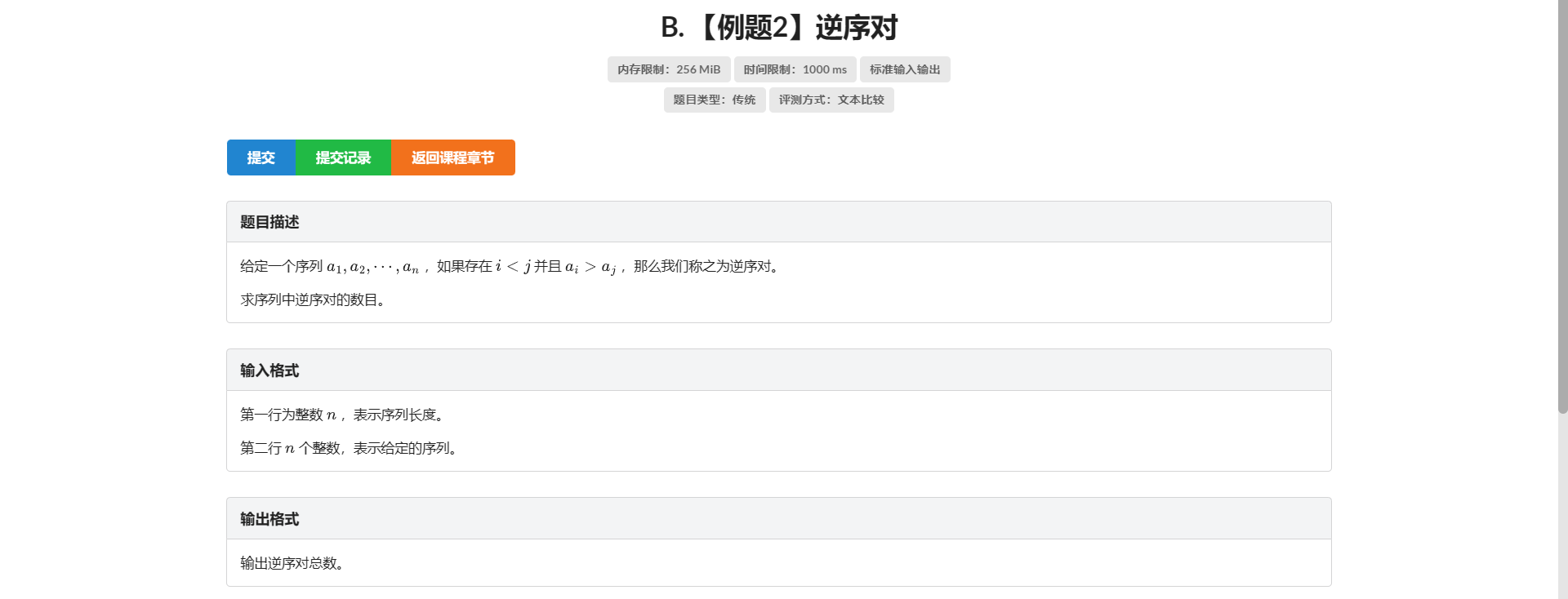
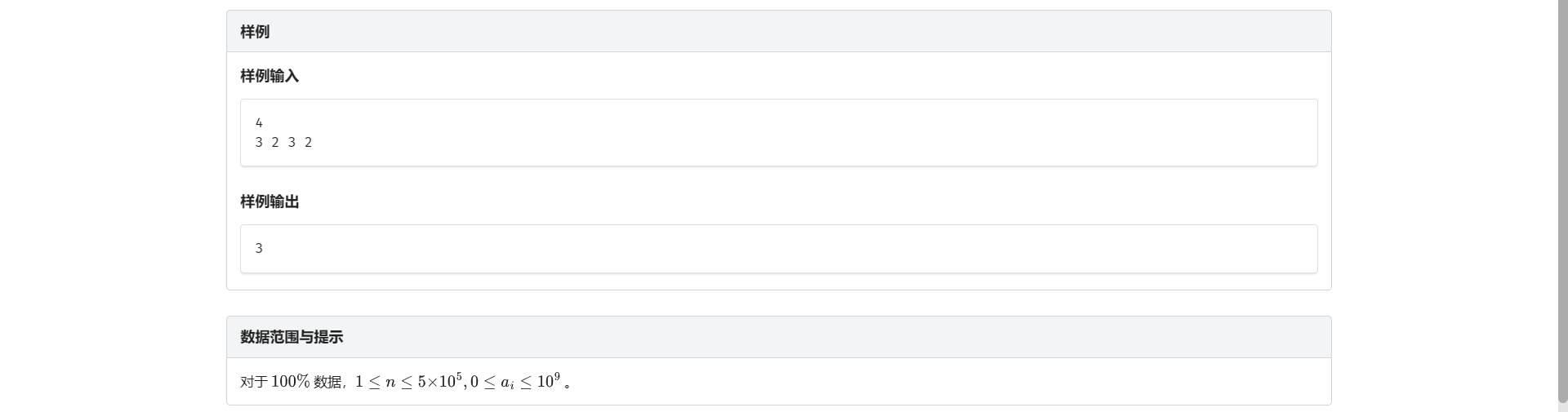
首先我们考虑暴力枚举 对每个 \(i\) 搜索其位置之后暴力枚举满足 \(a_i > a_j\) 的数对
然后发现实际上就是查询位于 \(i\) 之后并且小于 \(a_i\) 的数个数
进而想到用权值树状数组做
首先我们把整个数组都插入权值树状数组
然后每次 \(i\) 移动之后就把该数出现次数--即可
但是实际上有个小优化 如果是把 \(i\) 从右往左移 那么就不需要提前插入
显然倒过来把 \(j\) 从左往右移也是一个道理
本题 \(a_i \le 10^9\) 需要离散化
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define int long long
using namespace std;
const int N = 1e6 + 0721;
int a[N], f[N], b[N];
int n, m, sum;
ll ans;
int lowbit(int x) { return x & (-x); }
ll cx(int x) {
ll val = 0;
while (x) {
val += f[x];
x -= lowbit(x);
}
return val;
}
void xg(int x, int v) {
while (x <= m) {
f[x] += v;
// cout<<x<<" "<<f[x]<<endl ;
x += lowbit(x);
}
}
signed main() {
int n;
scanf("%lld", &n);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
memcpy(b, a, sizeof(a));
sort(b + 1, b + 1 + n);
m = unique(b + 1, b + 1 + n) - b - 1;
for (int i = 1; i <= n; ++i) a[i] = lower_bound(b + 1, b + 1 + m, a[i]) - b;
for (int i = 1; i <= n; ++i) {
xg(a[i], 1);
sum++;
ans += sum - cx(a[i]);
}
cout << ans;
return 0;
}
C.严格上升子序列数
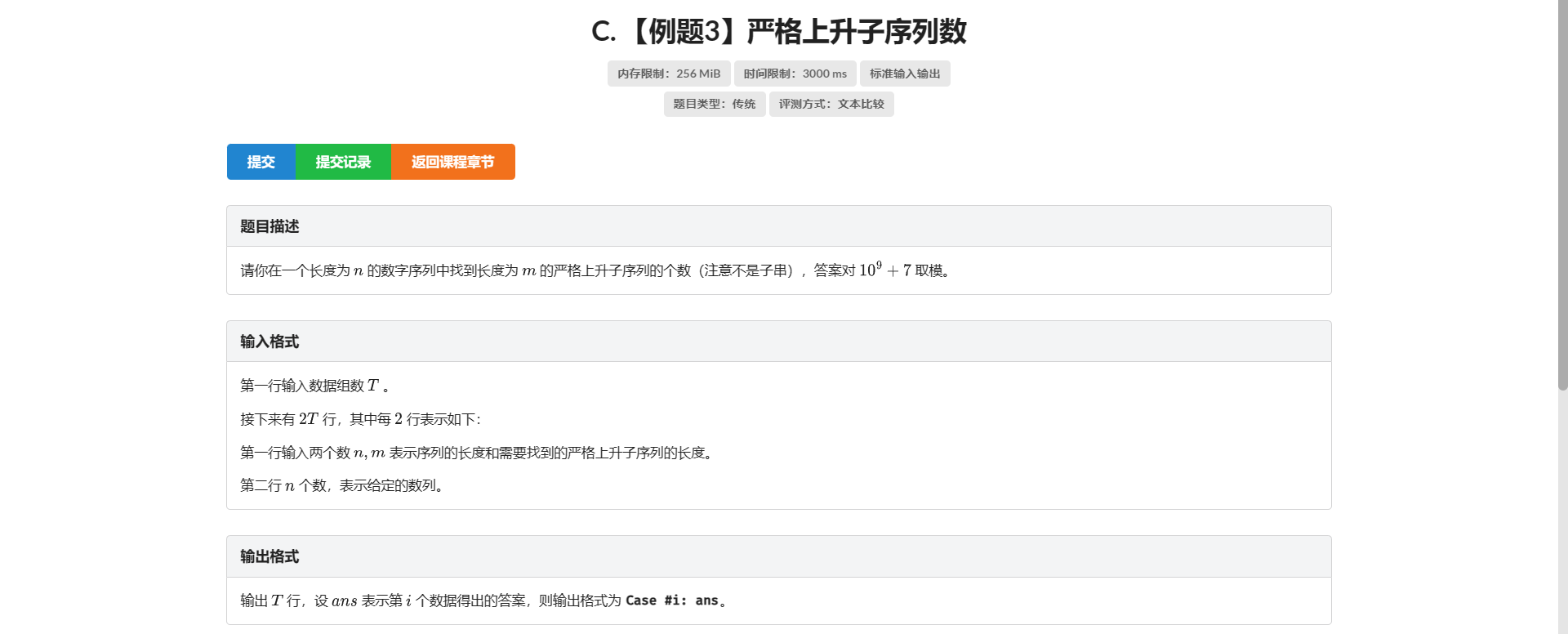
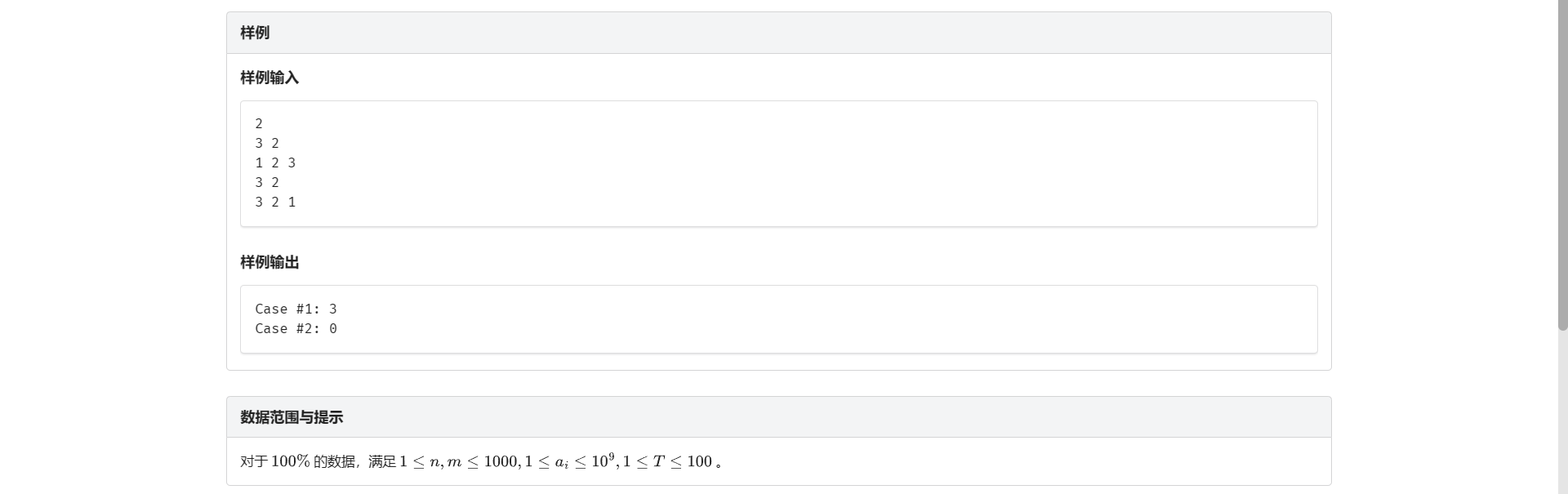
看到子序列类题目 想到设状态 \(f[i]\) 表示以 \(i\) 结尾的···
又因为这题要求长度为 \(m\) 的严格上升子序列 所以我们再扩一维
设 \(f[i][j]\) 表示以 \(i\) 结尾 长度为 \(j\) 的子序列个数
考虑转移 显然有 \(f[a_i][j] = \sum\limits_{k=1}^{i-1} f[a_k][j - 1] (a_k < a_i)\)
然后这个玩意长得就很像逆序对 \(DP\)
所以就拿树状数组优化就行了
这里有个小优化:因为 \(i\) 和 \(j\) 的枚举顺序没有强制要求 所以可以外层循环 \(j\) 这样开一维树状数组每次清空就够用
还有个小优化:由于转移只和 \(j\) 与 \(j - 1\) 有关 所以开两个一维数组 \(memcpy\) 就够用
当然不打以上两个小优化这题空间也是绰绰有余的
同样需要离散化
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1001;
const int mod = 1e9 + 7;
int f[N], g[N], a[N], b[N], tr[N];
int n, T, m;
inline int lowbit(int x) { return x & (-x); }
inline void update(int x, int v) {
while (x <= n) {
tr[x] = (tr[x] + v) % mod;
x += lowbit(x);
}
}
inline int query(int x) {
int res = 0;
while (x) {
res = (res + tr[x]) % mod;
x -= lowbit(x);
}
return res;
}
signed main() {
scanf("%d", &T);
for (int ii = 1; ii <= T; ++ii) {
memset(a, 0, sizeof(a));
memset(f, 0, sizeof(f));
memset(b, 0, sizeof(b));
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
memcpy(b, a, sizeof(a));
sort(b + 1, b + 1 + n);
int tot = unique(b + 1, b + 1 + n) - b - 1;
for (int i = 1; i <= n; ++i) a[i] = lower_bound(b + 1, b + 1 + tot, a[i]) - b;
for (int i = 1; i <= n; ++i) f[i] = 1;
for (int j = 2; j <= m; ++j) {
memset(tr, 0, sizeof(tr));
memcpy(g, f, sizeof f );
memset(f, 0, sizeof f );
for (int i = 1; i <= n; ++i) {
f[i] += query(a[i] - 1);
f[i] %= mod;
update(a[i], g[i]);
}
}
int ans = 0;
for (int i = 1; i <= n; ++i) {
ans += f[i];
ans %= mod;
}
printf("Case #%d: %d\n", ii, ans);
}
return 0;
}
D.区间修改区间查询
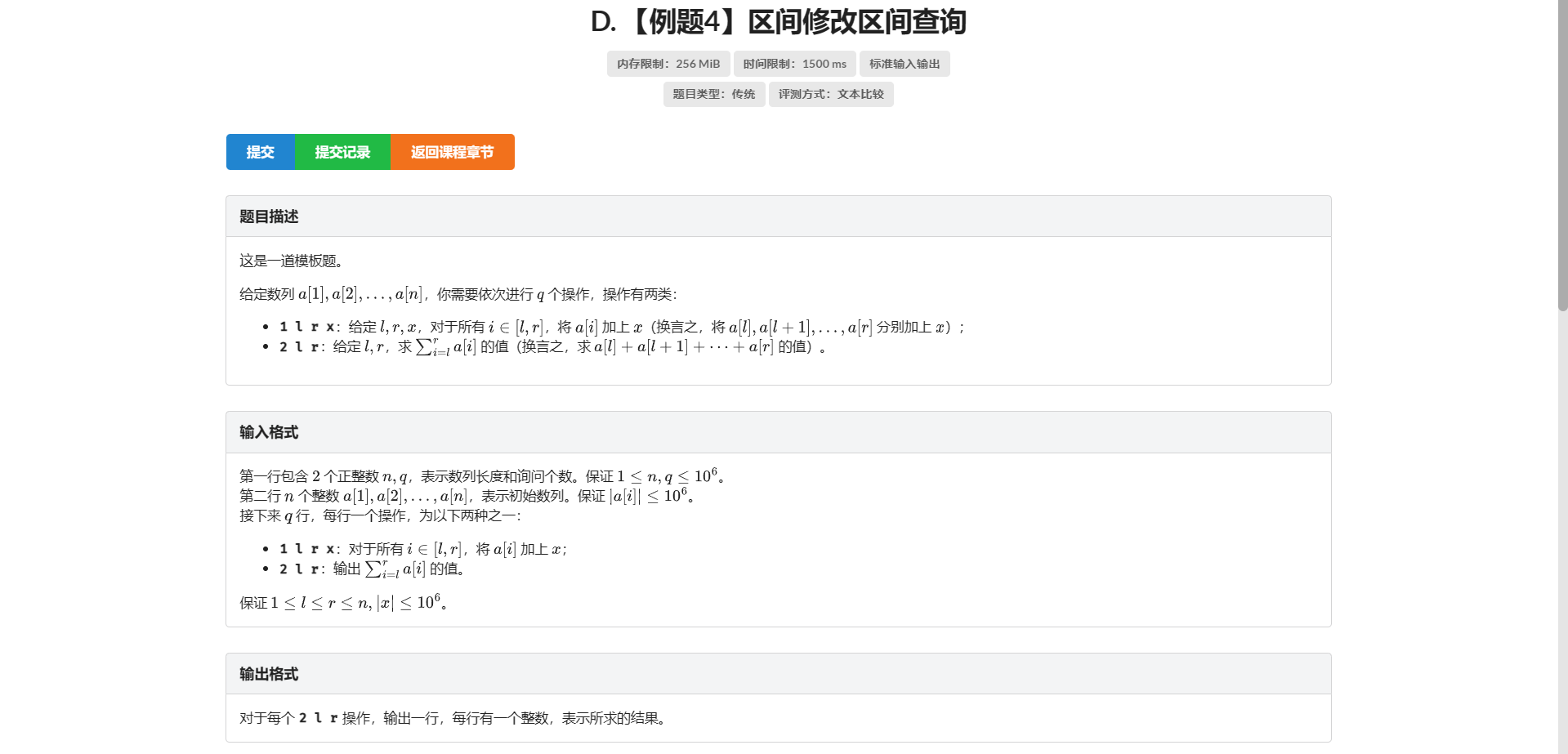
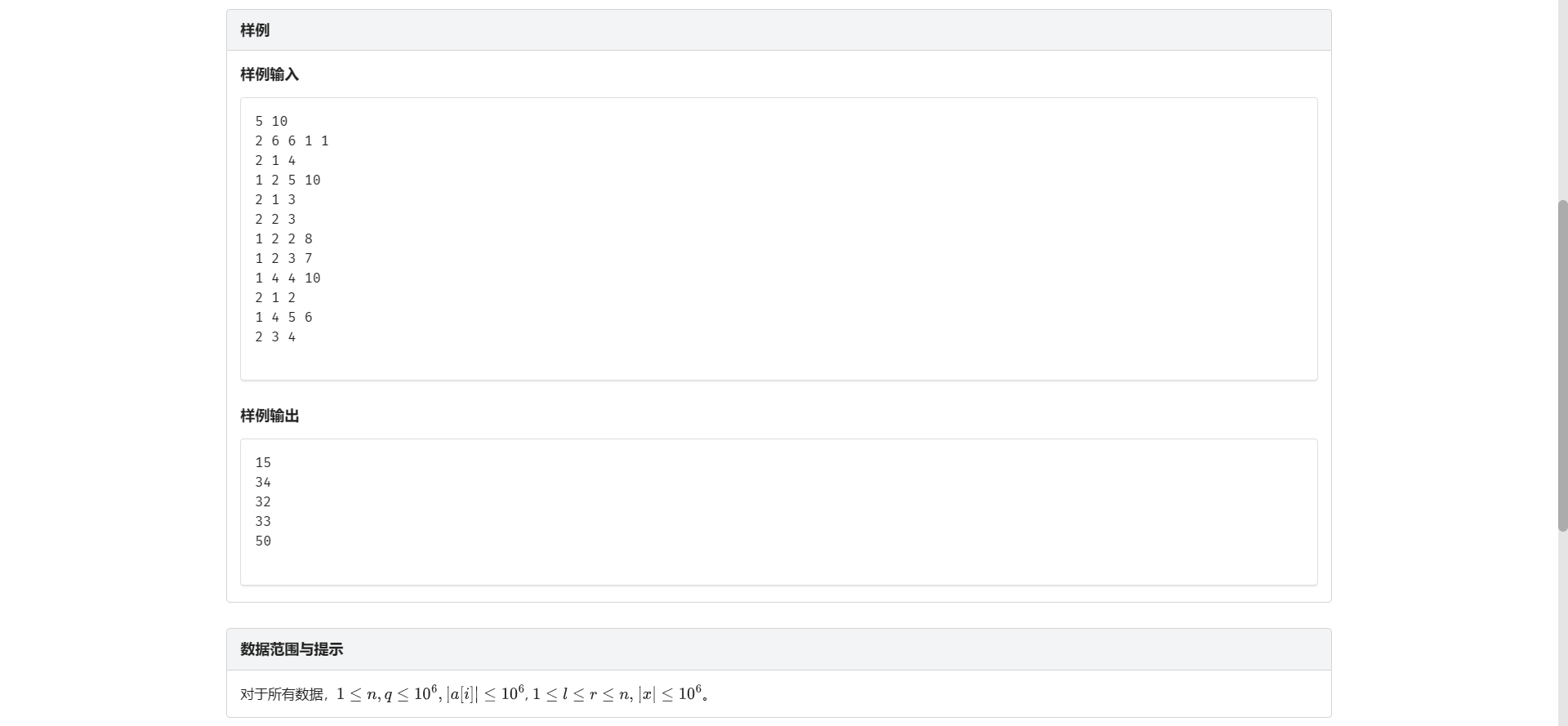
非常暴力的一个思路:一个个单点修改
然而这样复杂度还不如暴力做呢
考虑如何优化
因为树状数组是单点修改 然后思考单点修改怎么和区间修改扯上关系
突然想到差分
那么我们显然有 \(a_i = \sum\limits_{k=1}^id_k\)
那么 \(\sum\limits_{i=1}^na_i\) 就等于 \(\sum\limits_{i=1}^n\sum\limits_{k=1}^id_k\)
我们仔细观察这个式子 发现 \(d_1\) 出现了 \(n\) 次 \(d_2\) 出现了 \(n - 1\) 次 \(d_3\) 出现了 \(n - 2\) 次
进而发现 \(d_i\) 出现了 \(n - i + 1\) 次
那么就变成 \(\sum\limits_{i=1}^nd_i*(n - i + 1)\) = \((n + 1) * \sum\limits_{i=1}^nd_i - \sum\limits_{i=1}^nd_i * i\)
所以我们开两个树状数组 维护 \(\sum\limits_{i=1}^nd_i\) 和 \(\sum\limits_{i=1}^nd_i * i\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e6 + 0721;
ll tr1[N], tr2[N];
int a[N], d[N];
int n, q;
inline int lowbit(int x) { return x & (-x); }
inline void update1(int x, int v) {
while (x <= n) {
tr1[x] += (ll)v;
x += lowbit(x);
}
}
inline void update2(int x, ll v) {
while (x <= n) {
tr2[x] += v;
x += lowbit(x);
}
}
inline ll query1(int x) {
ll res = 0;
while (x) {
res += tr1[x];
x -= lowbit(x);
}
return res;
}
inline ll query2(int x) {
ll res = 0;
while (x) {
res += tr2[x];
x -= lowbit(x);
}
return res;
}
inline ll query(int x) {
return (ll)(x + 1) * query1(x) - query2(x); }
int main() {
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i) d[i] = a[i] - a[i - 1];
for (int i = 1; i <= n; ++i) {
update1(i, d[i]);
update2(i, (ll)d[i] * i);
}
while (q--) {
int num, l, r;
scanf("%d", &num);
if (num == 1) {
int val;
scanf("%d%d%d", &l, &r, &val);
update1(l, val);
update1(r + 1, -val);
update2(l, (ll)l * val);
update2(r + 1, (ll)(r + 1) * (-val));
}
else {
scanf("%d%d", &l, &r);
ll ans;
ans = query(r) - query(l - 1);
printf("%lld\n",ans);
}
}
return 0;
}
E.单点修改矩阵查询
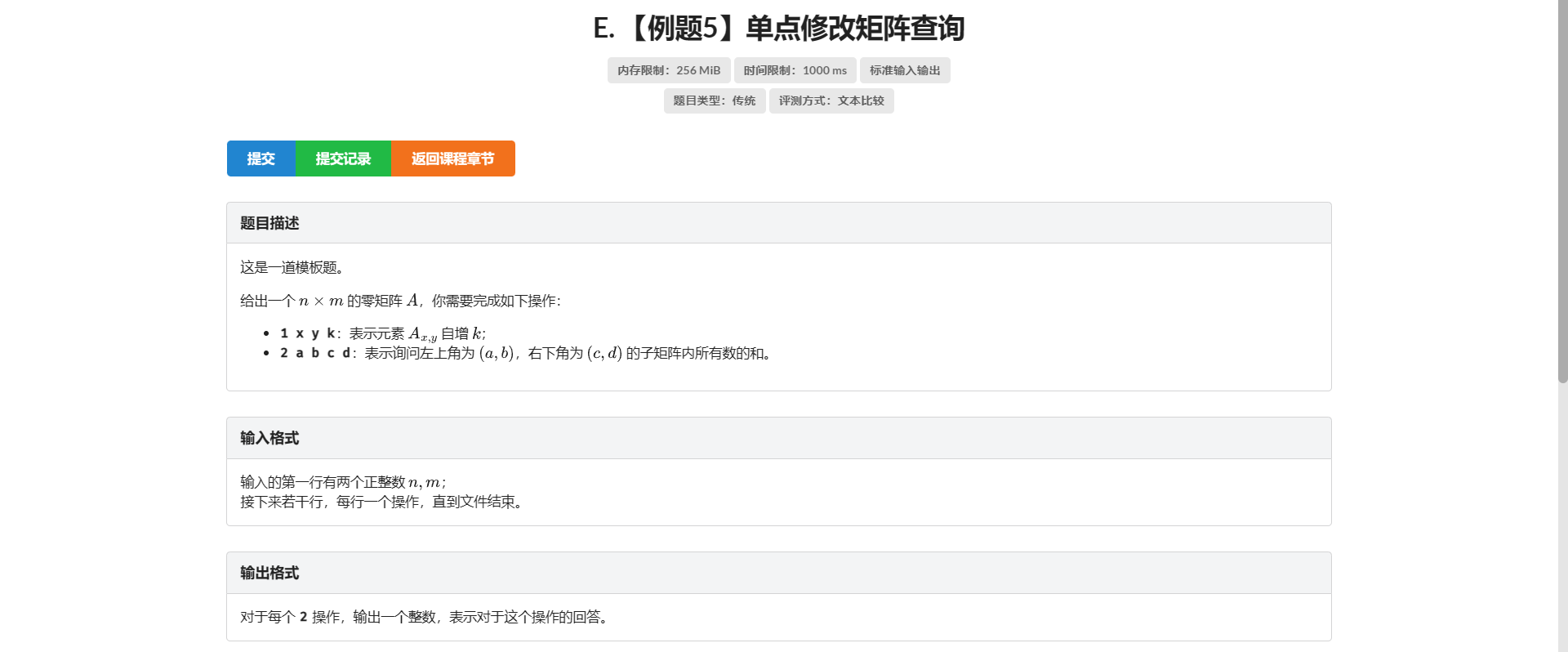
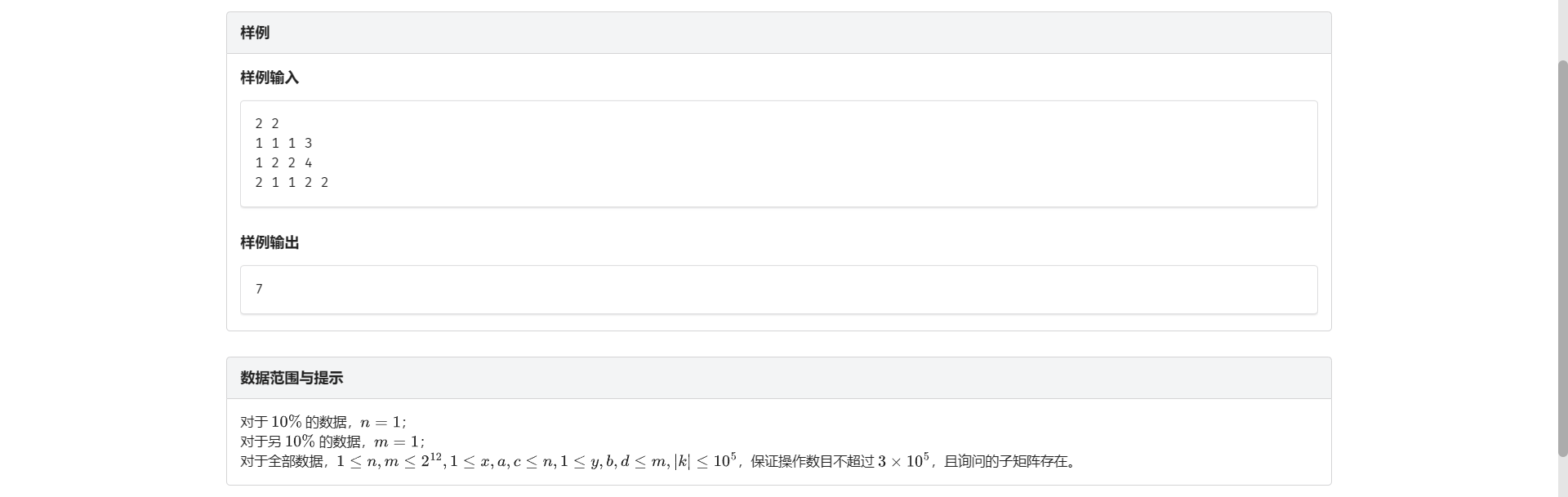
我们先不看题解 思考能不能做出来这题
首先查询很简单 就是那个非常典的二维容斥
然后我们考虑修改到底怎么做
在一维 我们 update(3) 的时候长这样
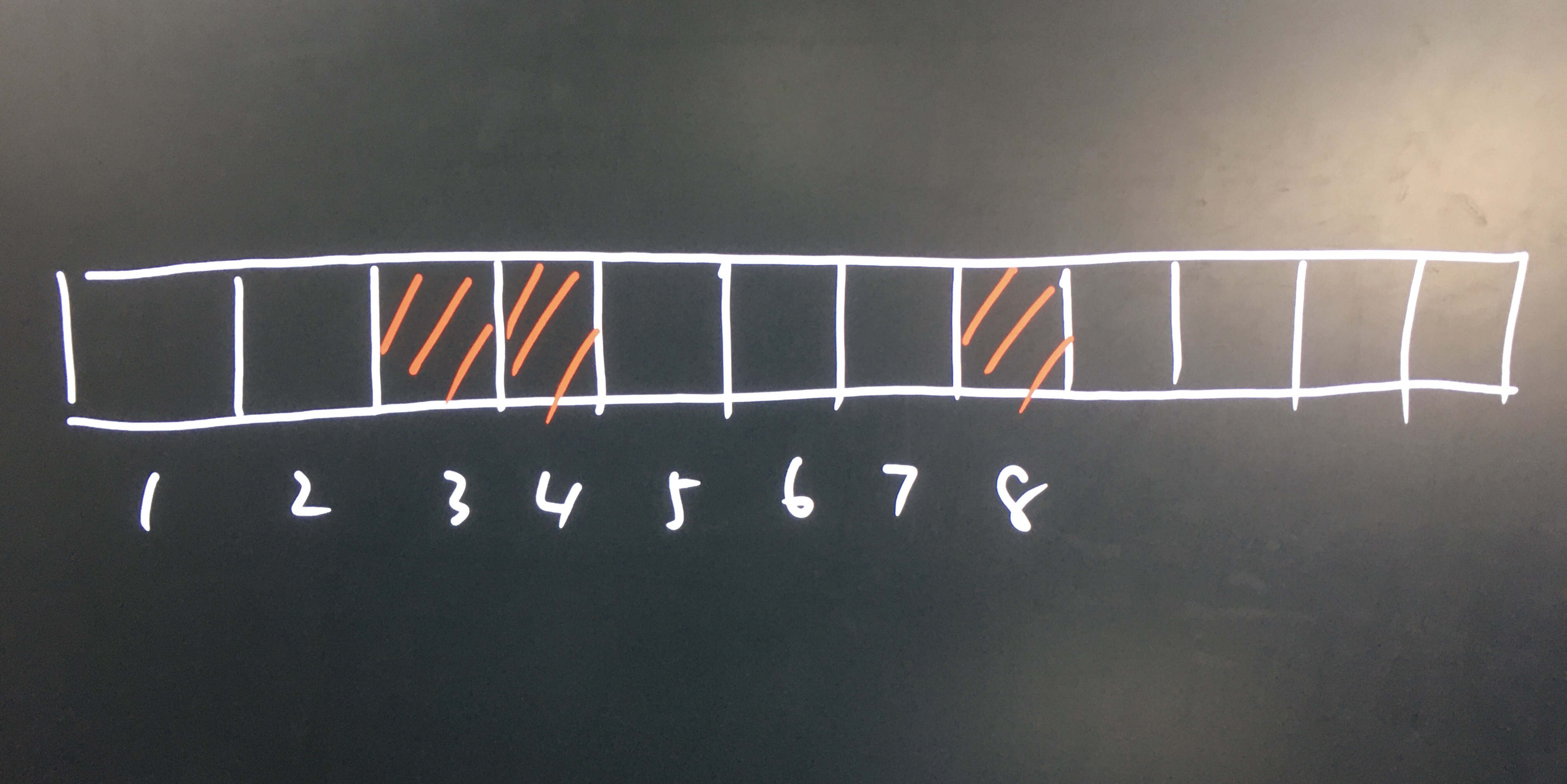
那么假如说我们要 update(3, 3) 那应该是长这样

那实际上我们套两层循环就能解决了
查询也同理
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = (1 << 12) + 10;
ll tr[N][N];
int a[N][N];
int n, m;
inline int lowbit(int x) { return x & (-x); }
inline void update(int x, int y, int v) {
for (int i = x; i <= n; i += lowbit(i)) {
for (int j = y; j <= m; j += lowbit(j)) tr[i][j] += v;
}
}
inline ll query(int x, int y) {
ll res = 0;
for (int i = x; i; i -= lowbit(i)) {
for (int j = y; j; j -= lowbit(j)) res += tr[i][j];
}
return res;
}
int main() {
scanf("%d%d", &n, &m);
int num;
while (scanf("%d", &num) != EOF) {
if (num == 1) {
int x, y, val;
scanf("%d%d%d", &x, &y, &val);
update(x, y, val);
}
else {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
ll ans;
ans = query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1);
printf("%lld\n",ans);
}
}
return 0;
}
F.矩阵修改矩阵查询
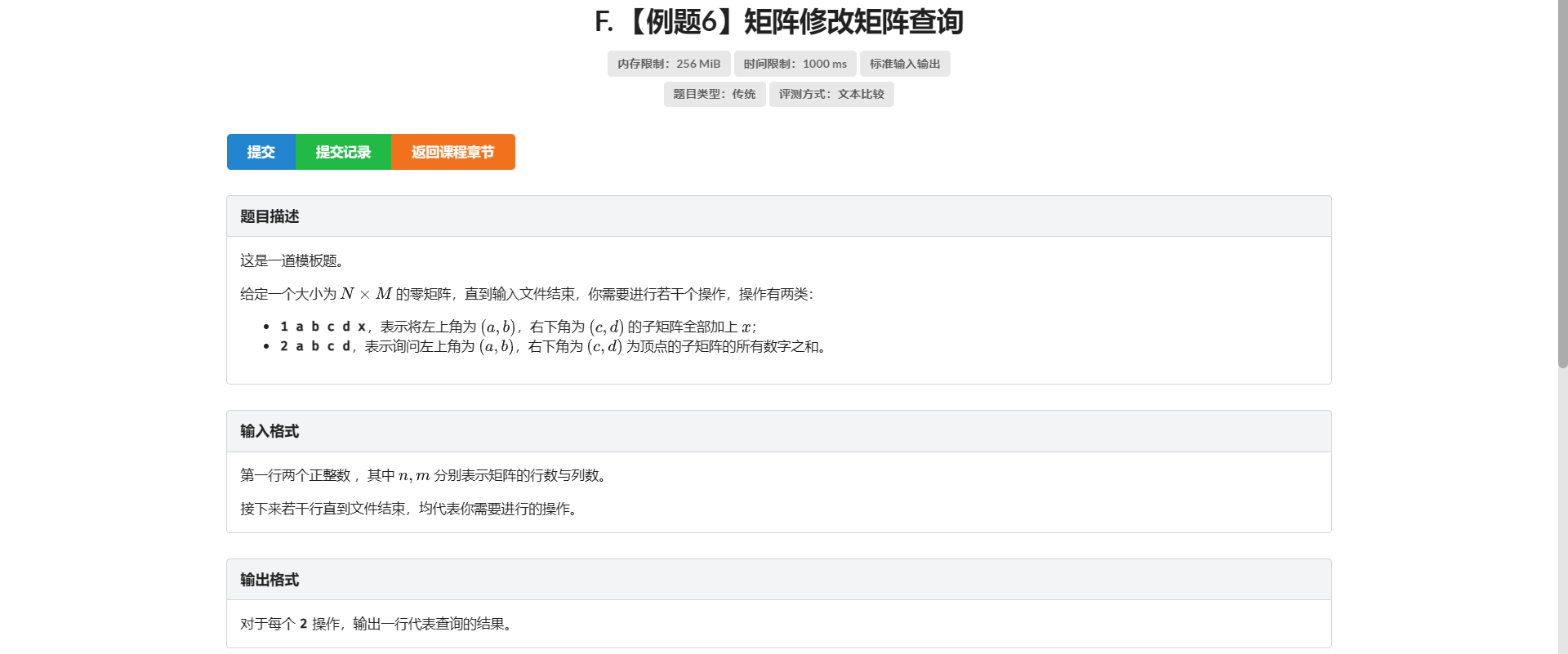
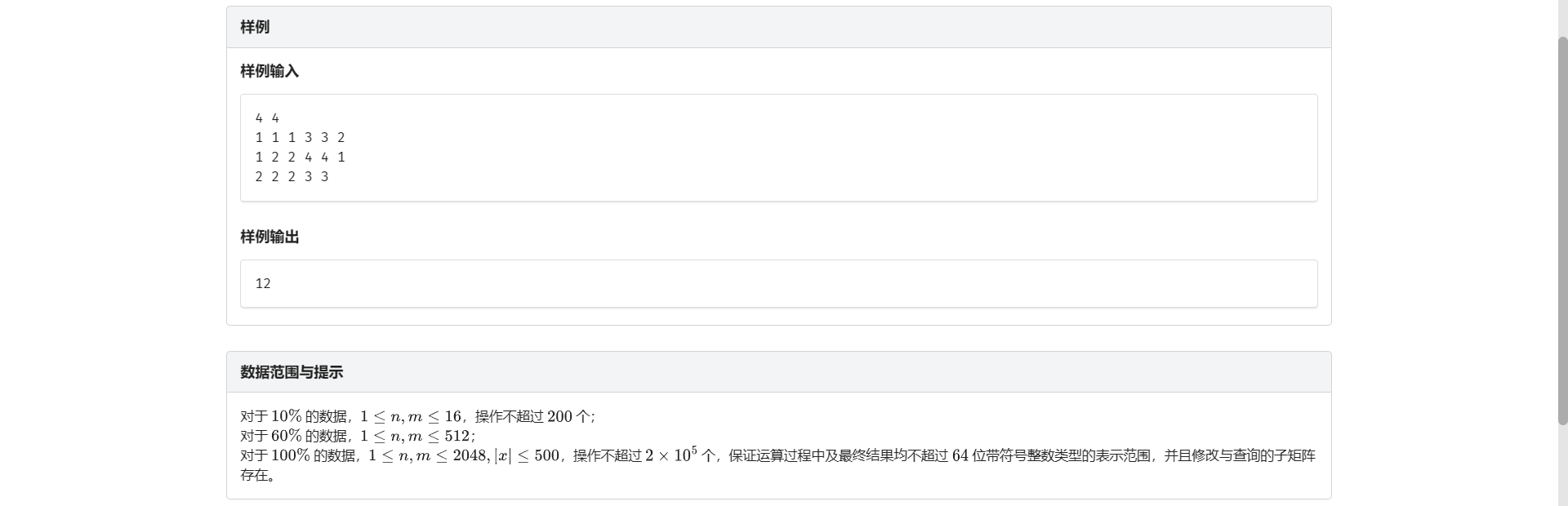
同理嘛 首先我们考虑普通的二维差分怎么做
对于 \((x1, y1) - (x2, y2)\) 的区间修改
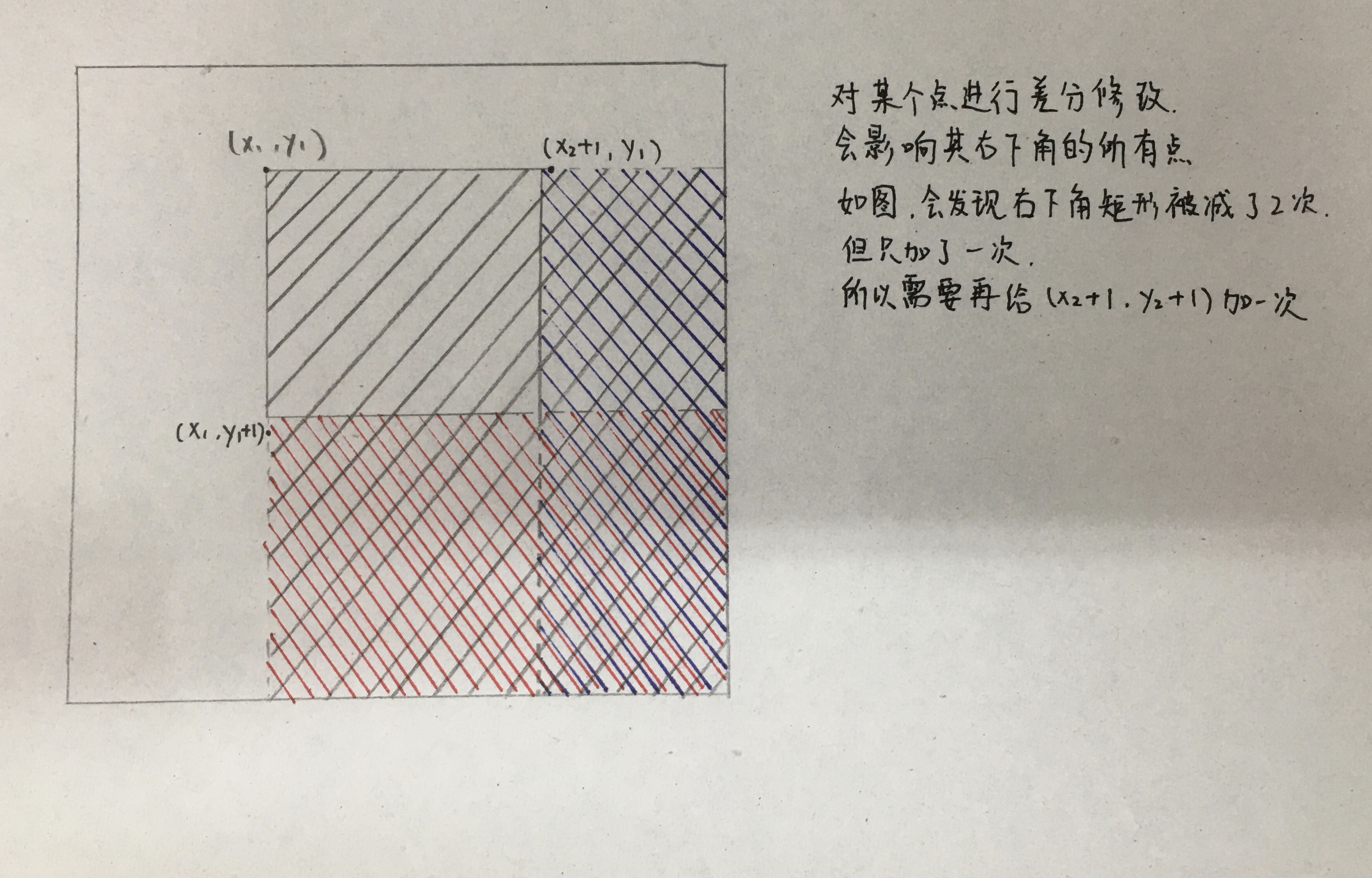
考虑怎么推柿子
对于一维的 \(x\) 层面 我们有 \(d_i\) 出现了 \(n - i + 1\) 次
那么在 \(y\) 层面 \(d_j\) 也出现了 \(m - j + 1\) 次
那么 \(d_{i, j}\) 就一共出现了 \((n - i + 1) * (m - j + 1)\) 次
那么式子就是 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^md_{i, j} * (n - i + 1) * (m - j + 1)\)
然后把 \((n + 1)\) 和 \((m + 1)\) 作为整体多项式展开
就有 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^md_{i, j} * \left[(n + 1) * (m + 1) - i * (m + 1) - j * (n + 1) + i * j\right]\)
再变个形就是 \((n + 1) * (m + 1) * \sum\limits_{i=1}^n\sum\limits_{j=1}^md_{i, j} - (m + 1) * \sum\limits_{i=1}^n\sum\limits_{j=1}^md_{i, j} * i - (n + 1) * \sum\limits_{i=1}^n\sum\limits_{j=1}^md_{i, j} * j + \sum\limits_{i=1}^n\sum\limits_{j=1}^md_{i, j} * i * j\)
所以我们开四个树状数组维护即可
点击查看代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const signed N = 0x0d00;
int tr1[N][N], tr2[N][N], tr3[N][N], tr4[N][N];
int n, m;
inline int lowbit(int x) { return x & (-x); }
inline void update(int x, int y, int v) {
for (int i = x; i <= n; i += lowbit(i)) {
for (int j = y; j <= m; j += lowbit(j)) {
tr1[i][j] += v;
tr2[i][j] += v * x;
tr3[i][j] += v * y;
tr4[i][j] += v * x * y;
}
}
}
inline int query(int x, int y) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) {
for (int j = y; j; j -= lowbit(j)) {
res += (x + 1) * (y + 1) * tr1[i][j] - (x + 1) * tr3[i][j] - (y + 1) * tr2[i][j] + tr4[i][j];
}
}
return res;
}
signed main() {
scanf("%lld%lld", &n, &m);
int num;
while (scanf("%lld", &num) != EOF) {
if (num == 1) {
int x1, x2, y1, y2, k;
scanf("%lld%lld%lld%lld%lld", &x1, &y1, &x2, &y2, &k);
update(x1, y1, k);
update(x2 + 1, y1, -k);
update(x1, y2 + 1, -k);
update(x2 + 1, y2 + 1, k);
int ans;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
x1 = x2 = i, y1 = y2 = j;
ans = query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1), +query(x1 - 1, y1 - 1);
}
}
} else if (num == 2) {
int x1, x2, y1, y2;
scanf("%lld%lld%lld%lld", &x1, &y1, &x2, &y2);
int ans;
ans = query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1);
printf("%lld\n", ans);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
x1 = x2 = i, y1 = y2 = j;
ans = query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1), +query(x1 - 1, y1 - 1);
}
}
}
}
return 0;
}
G.星星问题

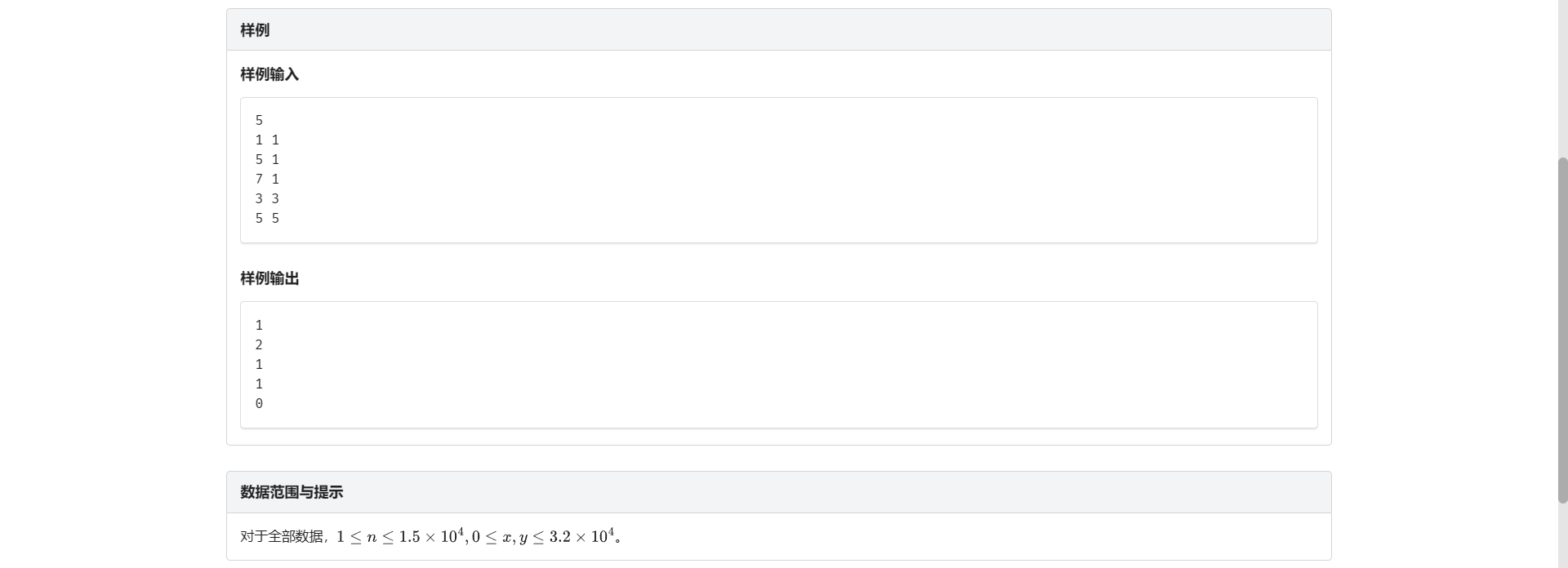
对于第 \(i\) 个点 要求的就是 \(x \le x_i\) 并且 \(y \le y_i\) 的点的数量
这就是个二维偏序
但是注意对于 \(x\) 相同的点 要先插 \(y\) 小的
并且最好先查再插自己
坑点:
- 横纵坐标可能为零 推荐读入之后++
- 坐标最大值不一定为 \(n\) update 的时候要处理到最大值
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 1e5 + 0721;
int n;
int ans[N];
struct node {
int x, y;
friend bool operator<(node x, node y) {
if (x.x != y.x) return x.x < y.x;
else return x.y < y.y;
}
} a[N];
struct BIT {
int tr[N];
inline int lowbit(int x) {
return x & (-x);
}
void update(int x, int val) {
while (x <= 40000) {
tr[x] += val;
x += lowbit(x);
}
}
int query(int x) {
int ret = 0;
while (x) {
ret += tr[x];
x -= lowbit(x);
}
return ret;
}
} bit;
void main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d%d", &a[i].x, &a[i].y);
++a[i].x, ++a[i].y;
}
sort(a + 1, a + 1 + n);
for (int i = 1; i <= n; ++i) {
int sum = bit.query(a[i].y);
++ans[sum];
bit.update(a[i].y, 1);
}
for (int i = 0; i < n; ++i) printf("%d\n", ans[i]);
}
}
int main() {
steven24::main();
return 0;
}
/*
5
1 1
5 1
7 1
3 3
5 5
*/
H.交换序列
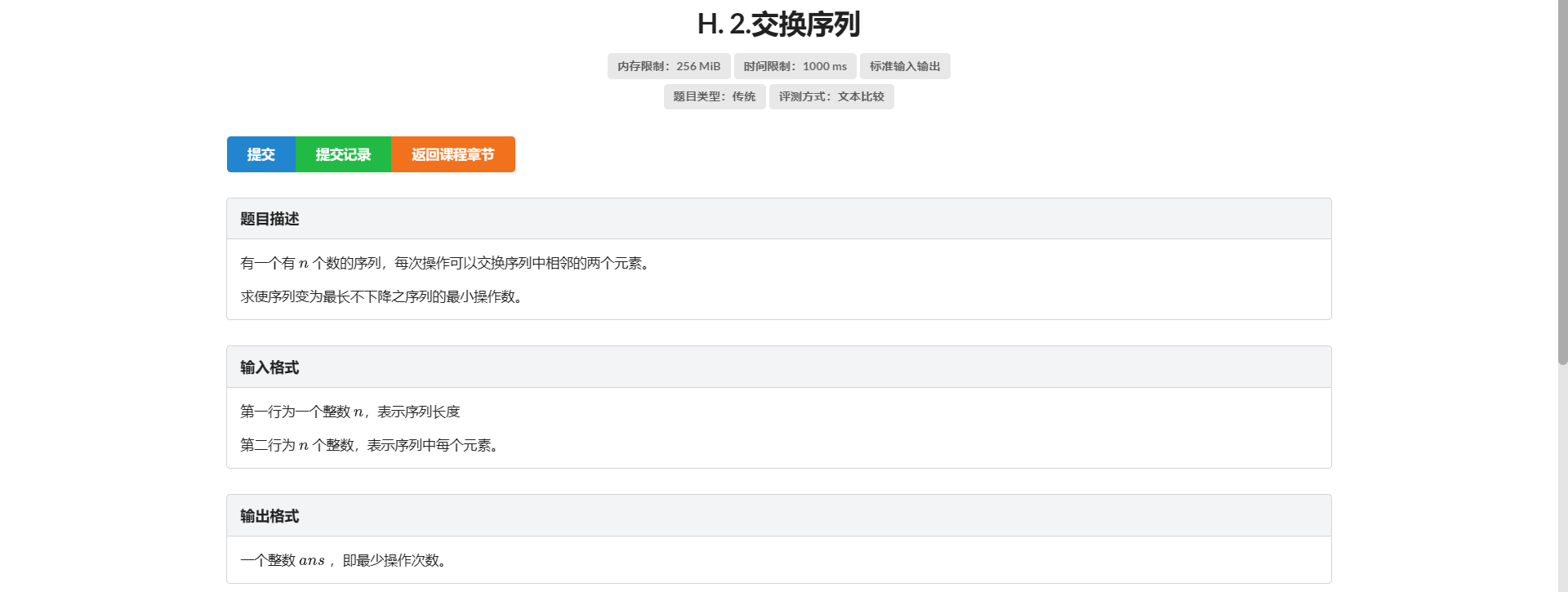
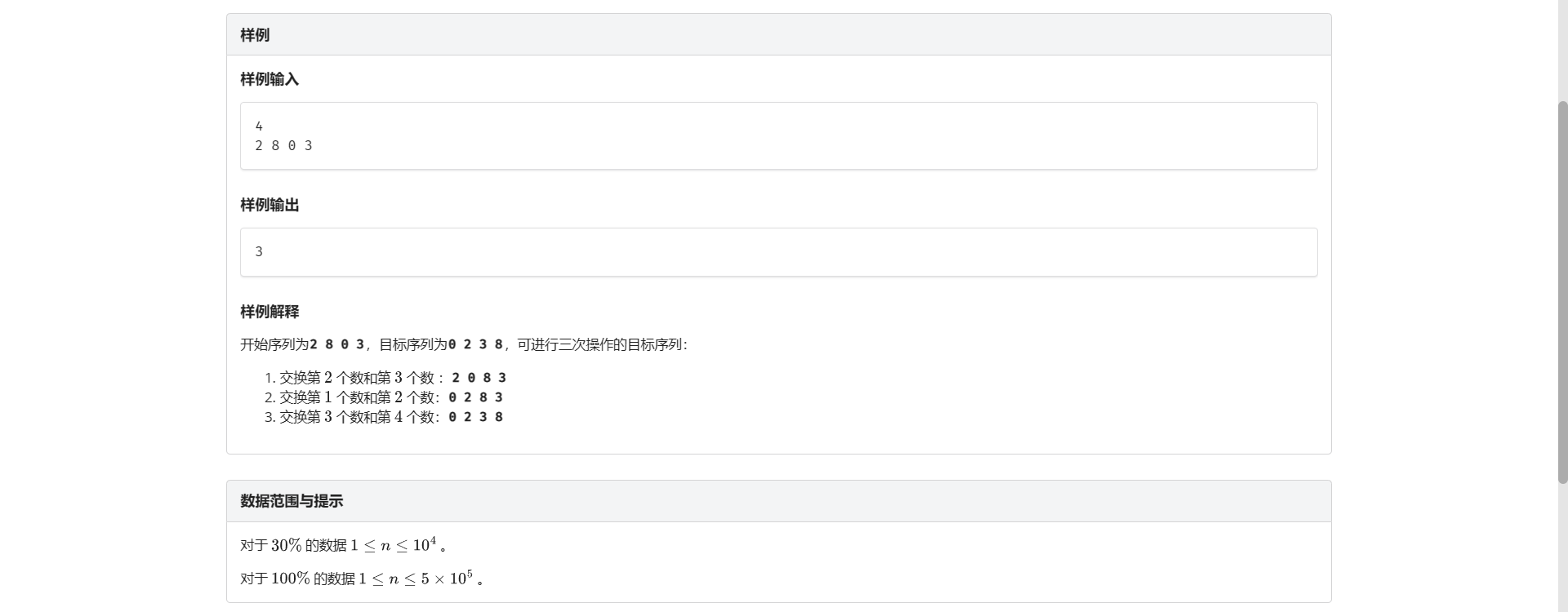
这题在树状数组 感觉有点像逆序对
搓了下样例感觉没啥问题打算交一发试试
结果它过了。。。
考虑每一个数 它前面有多少大于它的数就要交换这个次数
- 为什么
假设对于第 \(i\) 个数而言 前 \(i - 1\) 如果都已经交换好
那么前面 \(i - 1\) 就是一个递增序列
那么显然对于 \(i\) 的交换数就是大于它的数
代码就是从 B 题粘过来的
I.维护差数
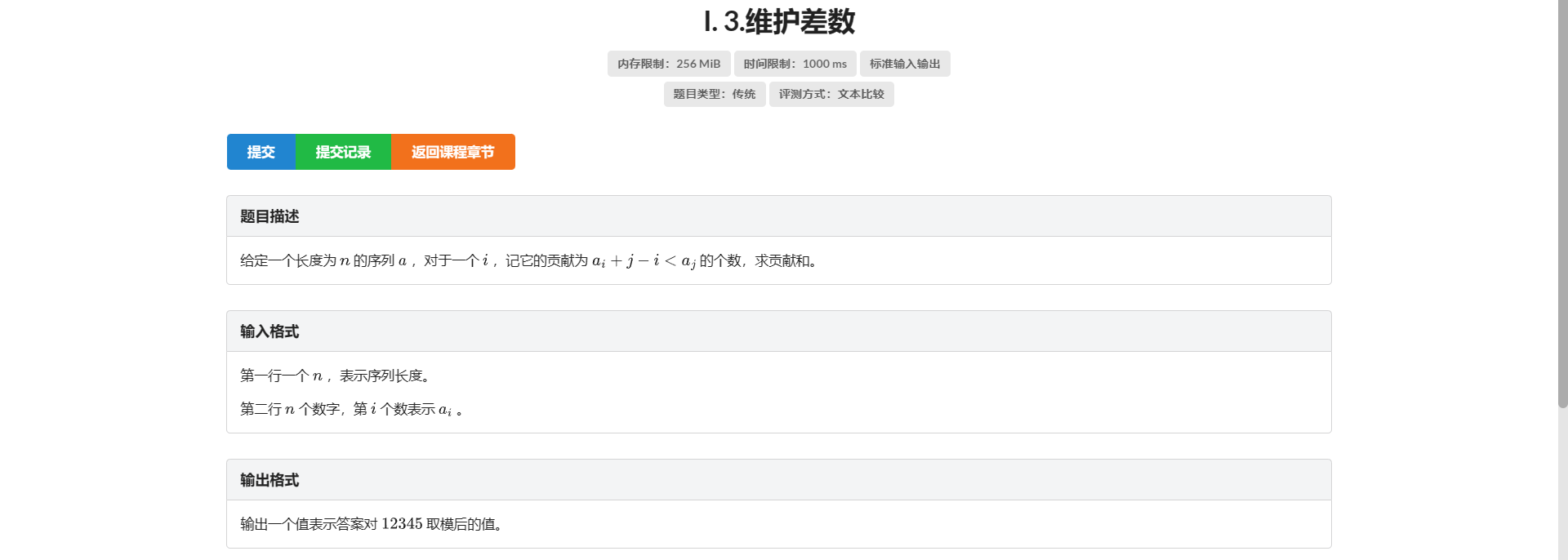
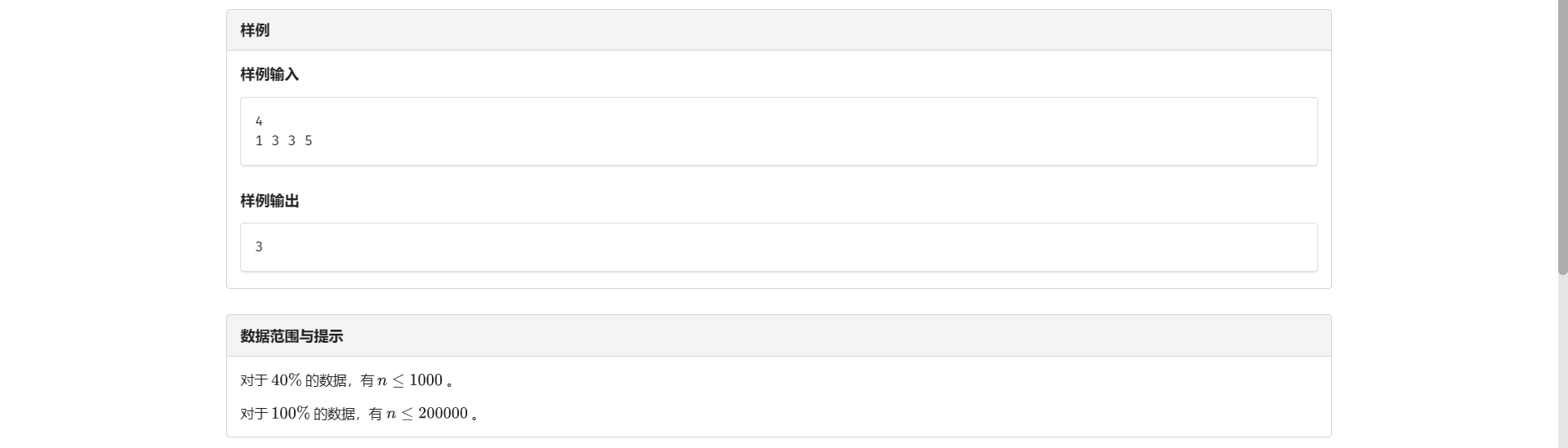
强烈诋毁这个题面
对于 \(i\) 的贡献是满足 \(a_i + j - i < a_j\) 并且有 \(j > i\) 的对数
并且保证 \(a_i \le n\)
不给值域没法做这题 因为不能离散化
考虑改写上面那个式子变成 \(a_i - i < a_j - j\)
没了 跟逆序对一样的做法
- 注意 \(a_i - i\) 可能为负 保守起见输入后同一给所有 \(a_i\) 加上 \(n\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 2e5 + 0721;
const int mod = 12345;
int a[N], b[N];
ll ans;
int n, maxn;
struct tree_array {
int tr[N];
inline int lowbit(int x) {
return x & (-x);
}
int query(int x) {
int ret = 0;
while (x) {
ret += tr[x];
x -= lowbit(x);
}
return ret;
}
void update(int x, int val) {
while (x <= maxn) {
tr[x] += val;
x += lowbit(x);
}
}
} bit;
void discritization() {
for (int i = 1; i <= n; ++i) {
a[i] += n;
maxn = max(maxn, a[i]);
}
}
void main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
discritization();
for (int i = n; i >= 1; --i) {
bit.update(a[i] - i, 1);
ans = (ans + (n - i + 1) - bit.query(a[i] - i)) % mod;
}
printf("%lld\n", ans);
}
}
int main() {
steven24::main();
return 0;
}
/*
4
1 3 3 5
*/
J.秘密邮件
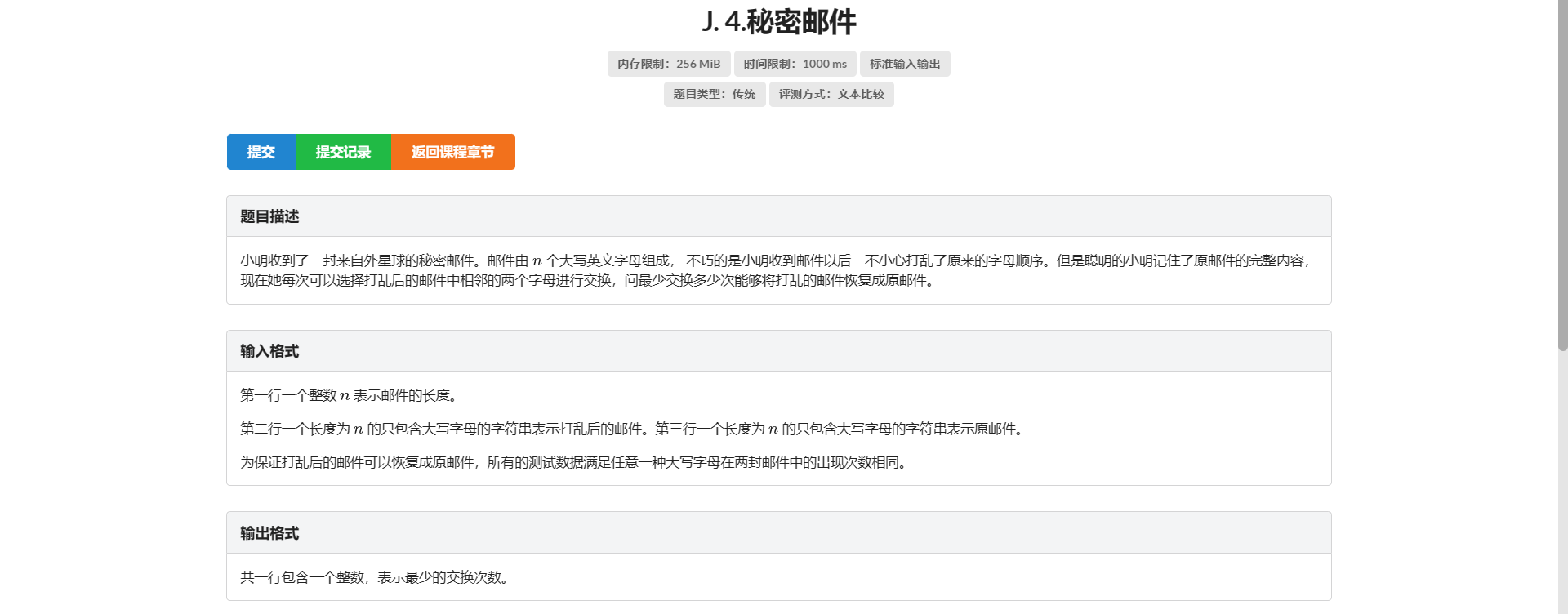
首先参考 H 题的优秀经验 考虑把这个东西转化成那玩意
那么对于目标串中的每一位 我们把 \(b_i\) 和 \(i\) 一一对应起来
然后我们把原串中按对应关系赋值 这样目标序列就是一个 \(1 - n\) 的排列
但是要考虑重复的情况 一个很直觉的做法就是对于一个字母 它在原串第 \(x\) 次出现的位置赋成它在目标串第 \(x\) 次出现的位置
考虑为什么这么做是对的
以 \(A\) 为例 这样做 我们对于原串中的每一个 \(A\) 都能保证前面所有的 \(A\) 都不对它产生贡献 这是很优的
考虑除了 \(A\) 以外的字母 在它之前出现的 \(A\) 的数量是一定的 假设它自己的值也一定 那么显然前面出现的 \(A\) 的值越小产生的贡献越少
写的时候从上题代码迁过来的 结果忘了改数组大小喜获 RE
点击查看代码
#include <bits/stdc++.h>
#pragma GCC optimize(2)
#define ll long long
using namespace std;
namespace steven24 {
const int N = 1e6 + 0721;
char c[N], b[N];
int a[N];
ll ans;
int n, maxn;
deque<int> loc[26];
struct tree_array {
int tr[N];
inline int lowbit(int x) {
return x & (-x);
}
int query(int x) {
int ret = 0;
while (x) {
ret += tr[x];
x -= lowbit(x);
}
return ret;
}
void update(int x, int val) {
while (x <= n) {
tr[x] += val;
x += lowbit(x);
}
}
} bit;
void main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf(" %c", &c[i]);
for (int i = 1; i <= n; ++i) scanf(" %c", &b[i]);
for (int i = 1; i <= n; ++i) {
int ch = b[i] - 'A';
loc[ch].push_back(i);
}
for (int i = 1; i <= n; ++i) {
int ch = c[i] - 'A';
a[i] = loc[ch].front();
loc[ch].pop_front();
}
for (int i = 1; i <= n; ++i) {
bit.update(a[i], 1);
ans += i - bit.query(a[i]);
}
printf("%lld\n", ans);
}
}
int main() {
steven24::main();
return 0;
}
/*
4
ABCD
DBCA
*/
K.二进制
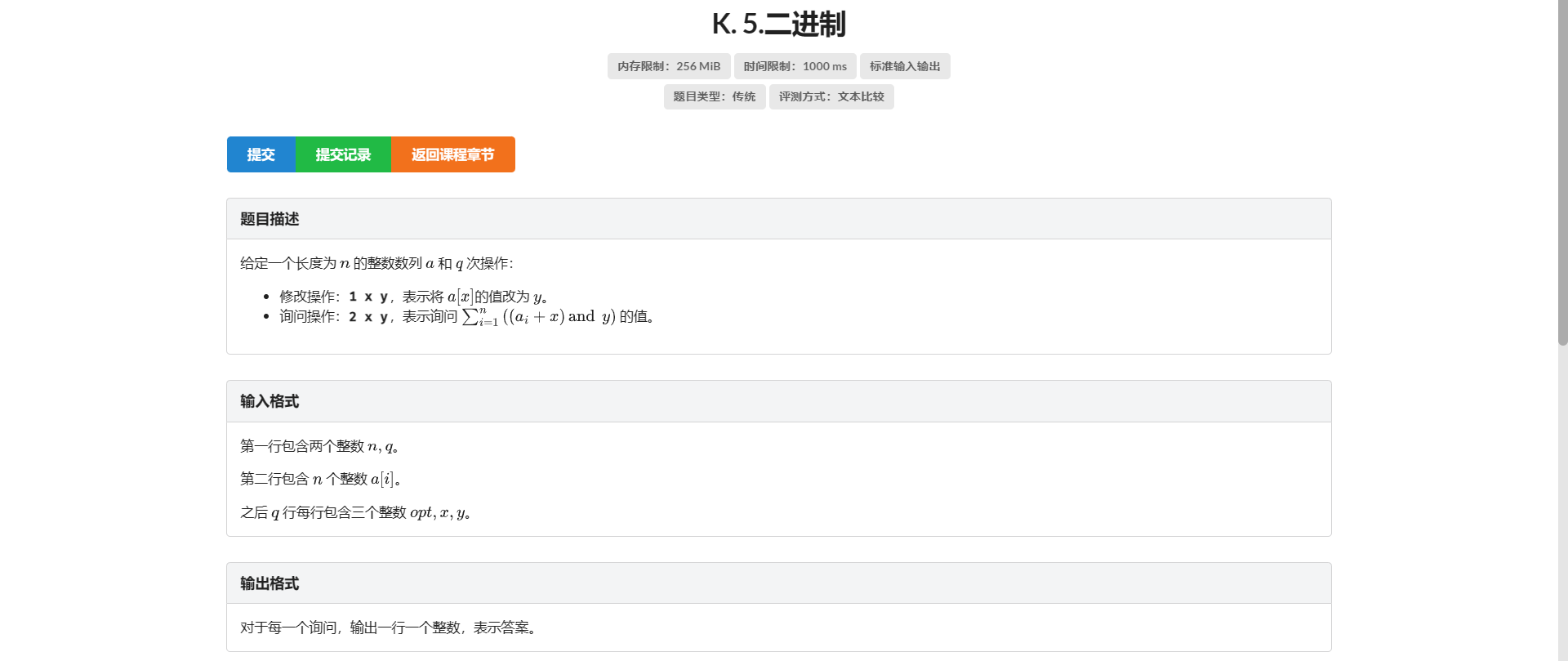
看到值域 想到二进制位拆开
可惜没想到二进制分解 \(y\) 神仙做法了属于是
考虑 \(x \text{ and } 2^k\) 的结果
显然当 \(x \in \left[0, 2^k - 1\right]\) 时 该结果为 \(0\)
当 \(x \in \left[2^k, 2^{k + 1} - 1\right]\) 时 该结果为 \(2^k\)
当 \(x \in \left[2^{k + 1}, 2^{k + 1} + 2 ^ k - 1 \right]\) 时 该结果为 \(0\)
它循环回去了
所以实际上我们在意的 就是 \(x \mod 2^{k + 1}\) 的结果
我们继续考虑对 \(y\) 进行二进制拆分
对于 \(y\) 的第 \(j\) 位二进制 如果它为 \(1\)
那么它对答案的贡献就是对 \(2^{j + 1}\) 取模后 位于 \(\left[2^j, 2^{j + 1} - 1\right]\) 的数的数量乘以 \(2^j\)
那么如果再加 \(x\) 那就是加上 \(x\) 之后 对 \(2^{j + 1}\) 取模后位于 \(\left[2^j, 2^{j + 1} - 1\right]\) 的数的数量
转化为对 \(2^{j + 1}\) 取模后位于 \(\left[2^j - x, 2^{j + 1} - 1 - x\right]\) 的数的数量
于是我们开 20 个 BIT
第 \(i\) 个 BIT 的第 \(j\) 位维护的就是对 \(2^{i + 1}\) 取模后结果为 \(j\) 的数的个数
那我们查对 \(2^{j + 1}\) 取模后位于 \(\left[2^j - x, 2^{j + 1} - 1 - x\right]\) 的数的数量实际就是一段区间查询
还剩一个问题:当 \(2^j - x < 0\) 时
实际挺好解决的 因为负数取模会变回正的 如果左右取模前都 \(<0\) 取模之后还是 \(l\) 在左 \(r\) 在右
我们真正要考虑的情况是 \(l\) 变负了 \(r\) 是正的 然后 \(l\) 取模后加上模数超过了 \(r\) 的情况
如图
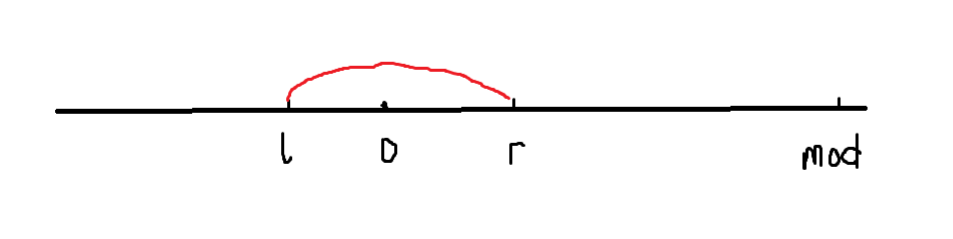
取完模之后 它变成了这样
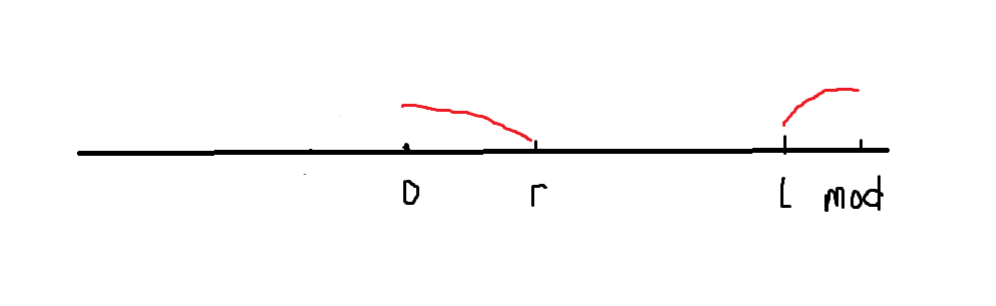
所以此时我们要查的就是 \(\left[0, r\right]\) 和 \(\left[l, mod\right]\) 这两段的和
(注意 BIT 的数组下标不为 0 所以实际第 \(j\) 位存储的是取模后为 \(j - 1\) 的数的数量)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 2e6 + 0721;
int a[N];
int n, q;
struct tree_array {
int tr[N];
inline int lowbit(int x) {
return x & (-x);
}
int query(int x) {
int ret = 0;
while (x) {
ret += tr[x];
x -= lowbit(x);
}
return ret;
}
void update(int x, int val, int maxn) {
while (x <= maxn) {
tr[x] += val;
x += lowbit(x);
}
}
} bit[20];
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
void main() {
n = read(), q = read();
for (int i = 1; i <= n; ++i) a[i] = read();
for (int i = 1; i <= n; ++i) {
for (int j = 0; j <= 19; ++j) bit[j].update(a[i] % (1 << (j + 1)) + 1, 1, (1 << (j + 1)));
}
while (q--) {
int opt, x, y;
opt = read(), x = read(), y = read();
if (opt == 1) {
for (int j = 0; j <= 19; ++j) {
bit[j].update(a[x] % (1 << (j + 1)) + 1, -1, (1 << (j + 1)));
bit[j].update(y % (1 << (j + 1)) + 1, 1, (1 << (j + 1)));
}
a[x] = y;
} else {
ll ans = 0;
// cout << "y = " << y << "\n";
for (int j = 0; j <= 19; ++j) {
if ((y & (1 << j)) == 0) continue;
// cout << j << " ";
int l = (1 << j), r = (1 << (j + 1)) - 1;
l = (l - 1 - x + (1 << 20)) % (1 << (j + 1));
r = (r - x + (1 << 20)) % (1 << (j + 1));
// cout << l << " " << r << "\n";
// cout << bit[j].query(r + 1) << " " << bit[j].query(l + 1) << "\n";
if (l <= r) ans += 1ll * (bit[j].query(r + 1) - bit[j].query(l + 1)) * (1 << j);
else ans += 1ll * (bit[j].query(r + 1) - bit[j].query(l + 1) + bit[j].query(1 << (j + 1))) * (1 << j);
}
printf("%lld\n", ans);
}
}
}
}
int main() {
steven24::main();
return 0;
}
/*
6 6
8 9 1 13 9 3
1 4 5
2 6 9
1 3 7
2 7 7
1 6 1
2 11 13
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号