YBTOJ 3.4强连通分量
A.有向图缩点
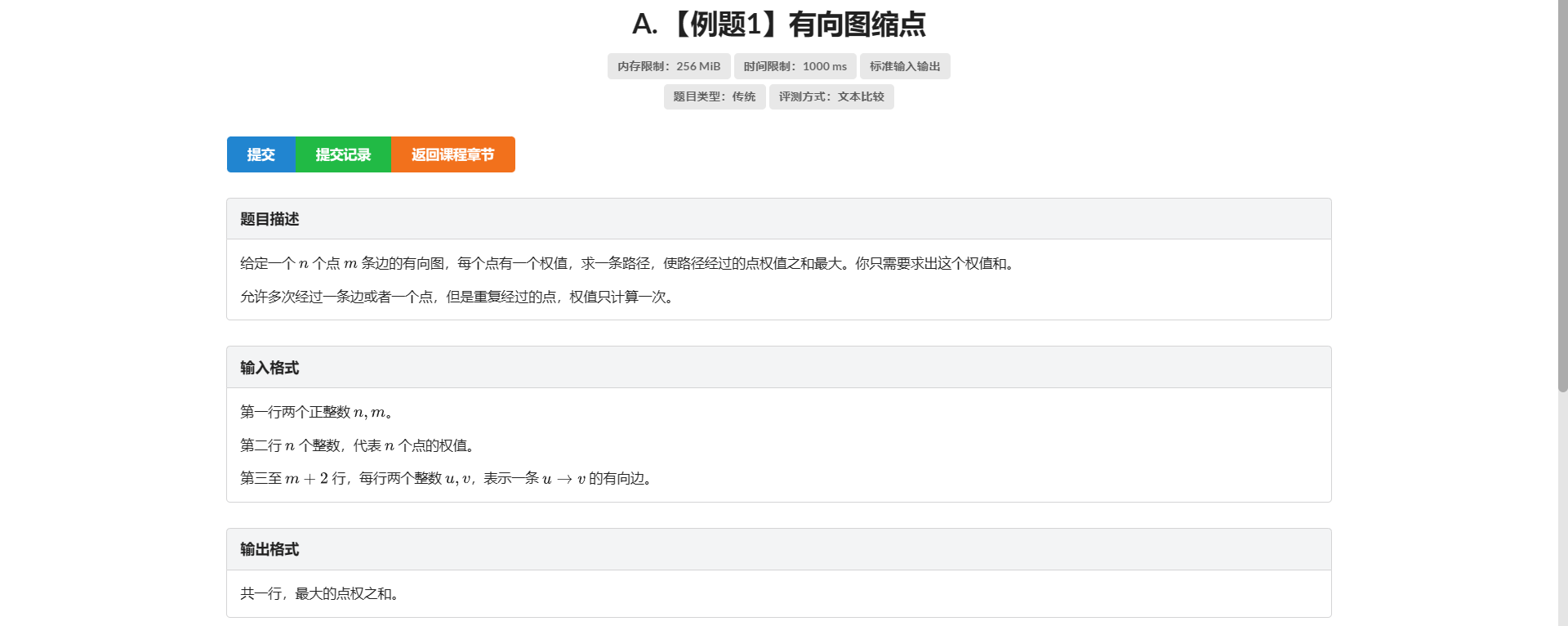
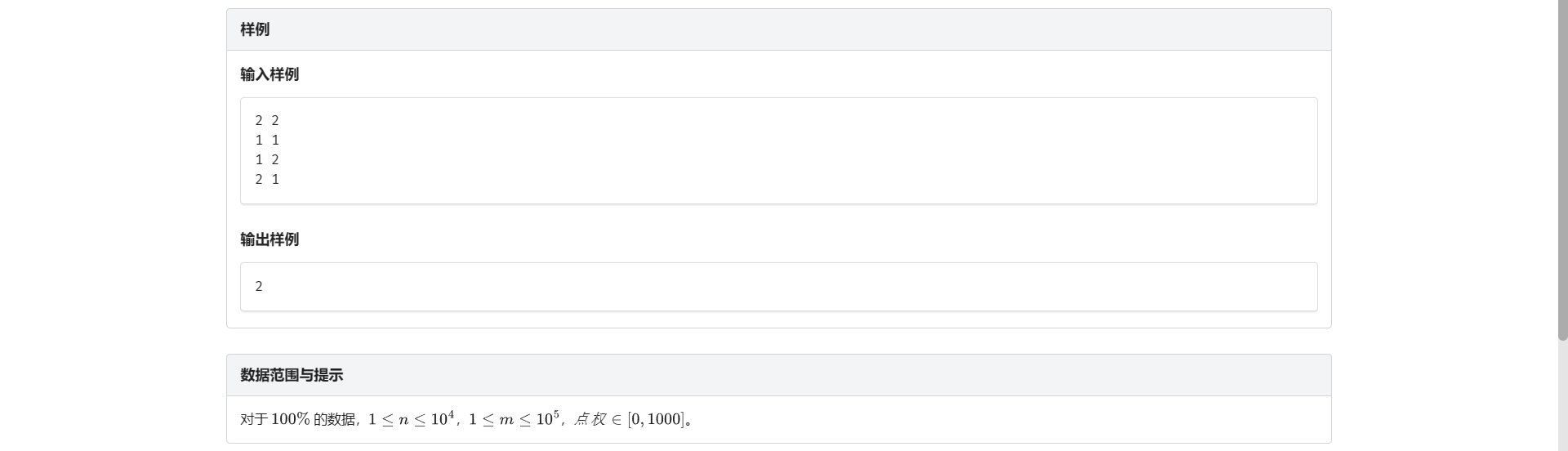
板子 讲解有时间补 咕
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 200721;
int head[N], nxt[N], to[N], v[N], cnt;
int sccnum[N], sccsz[N], dfn[N], low[N], dfs_clock, scccnt;
int _head[N], _nxt[N], _to[N], _cnt;
int sccrd[N], q[N], tpx[N], dp[N], top, tp;
int n, m, ans;
void cmb(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void _cmb(int x, int y) {
_to[++_cnt] = y;
_nxt[_cnt] = _head[x];
_head[x] = _cnt;
}
void tarjan(int x) {
dfn[x] = low[x] = ++dfs_clock;
q[++top] = x;
for (int i = head[x]; i; i = nxt[i]) {
// cout<<"1" ;
int y = to[i];
if (dfn[y] == 0)
tarjan(y), low[x] = min(low[x], low[y]);
else if (sccnum[y] == 0)
low[x] = min(low[x], dfn[y]);
}
// cout<<"1" ;
if (low[x] == dfn[x]) {
scccnt++;
while (1) {
int now = q[top];
top--;
sccnum[now] = scccnt;
sccsz[scccnt] += v[now];
// cout<<"1" ;
if (now == x)
break;
}
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &v[i]);
for (int i = 1; i <= m; ++i) {
int x, y;
scanf("%d%d", &x, &y);
cmb(x, y);
}
for (int i = 1; i <= n; ++i) {
if (dfn[i] == 0)
tarjan(i);
}
// cout<<"1" ;
for (int i = 1; i <= n; ++i) {
for (int j = head[i]; j; j = nxt[j]) {
int y = to[j];
if (sccnum[i] != sccnum[y]) {
_cmb(sccnum[i], sccnum[y]);
sccrd[sccnum[y]]++;
}
}
}
for (int i = 1; i <= scccnt; ++i) {
if (sccrd[i] == 0)
tpx[++tp] = i;
}
for (int i = 1; i <= tp; ++i) {
for (int j = _head[tpx[i]]; j; j = _nxt[j]) {
sccrd[_to[j]]--;
if (sccrd[_to[j]] == 0)
tpx[++tp] = _to[j];
}
}
for (int i = 1; i <= scccnt; ++i) {
dp[i] = sccsz[i];
}
for (int i = 1; i <= tp; ++i) {
for (int j = _head[tpx[i]]; j; j = _nxt[j]) dp[_to[j]] = max(dp[_to[j]], sccsz[_to[j]] + dp[tpx[i]]);
}
for (int i = 1; i <= scccnt; ++i) ans = max(ans, dp[i]);
printf("%d\n", ans);
// for( int i = 1 ; i <= n ; ++i )
// cout<<i<<" "<<sccnum[i]<<" "<<sccsz[sccnum[i]]<<endl ;
return 0;
}
upd:实际上 \(Tarjan\) 缩完点之后的编号顺序就是逆拓扑序 不需要排拓扑(
B.受欢迎的牛
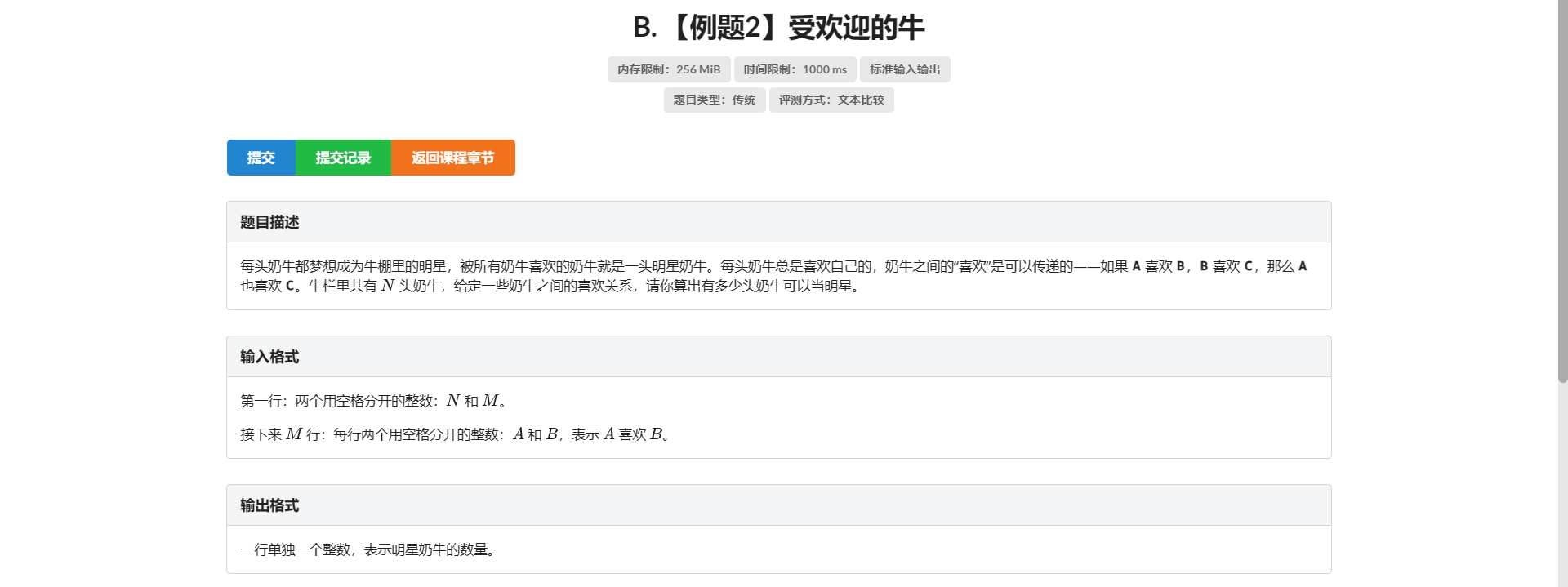
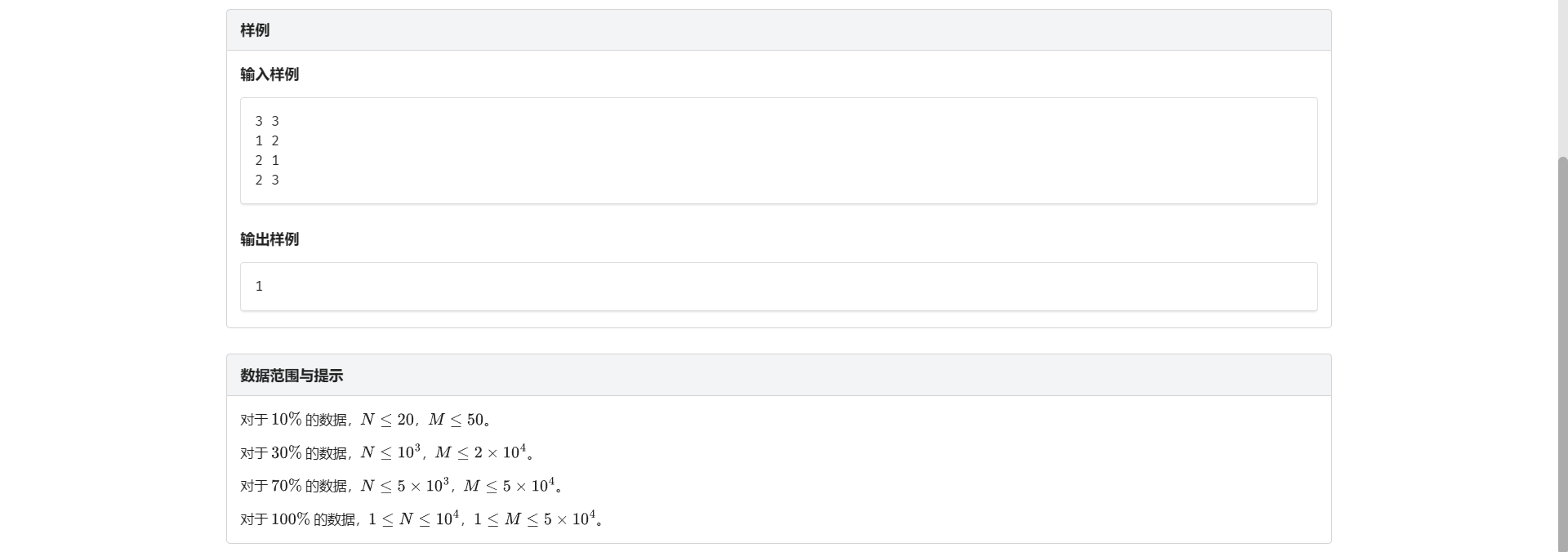
实际上受欢迎的牛就是从任何点出发 都能到达的点
想到 \(DAG\) 上的 \(DP\)
但是题目不保证图是个 \(DAG\)
这时发现一个强连通图里 所有的牛都互相喜欢 所以缩点对于信息没有影响
然后就可以跑缩点
然后就发现当缩完只有一个点的出度为 \(0\) 那么结尾那个强连通分量的所有点都是受欢迎的牛
否则就没有受欢迎的牛
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 50721;
int head[N], to[N], nxt[N], vis[N], sccnum[N], sccsz[N], rd[N], cd[N], dfn[N], low[N], s[N];
int n, m, cnt, scccnt, dfs_clock, top;
void cmb(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int u) {
vis[u] = 1;
dfn[u] = low[u] = ++dfs_clock;
s[++top] = u;
for (int i = head[u]; i; i = nxt[i]) {
if (!dfn[to[i]]) {
dfs(to[i]);
low[u] = min(low[u], low[to[i]]);
} else if (!sccnum[to[i]])
low[u] = min(low[u], dfn[to[i]]);
}
if (low[u] == dfn[u]) {
scccnt++;
while (1) {
int x = s[top];
top--;
sccnum[x] = scccnt;
sccsz[scccnt]++;
if (x == u)
break;
}
}
}
void sd(int x) {
for (int i = head[x]; i; i = nxt[i]) {
if (sccnum[x] != sccnum[to[i]]) {
cd[sccnum[x]]++;
rd[sccnum[to[i]]]++;
}
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int u, v;
scanf("%d%d", &u, &v);
cmb(u, v);
}
for (int i = 1; i <= n; i++) {
if (!vis[i])
dfs(i);
}
for (int i = 1; i <= n; i++) {
sd(i);
}
int sum = 0, mem;
for (int i = 1; i <= scccnt; i++) {
if (cd[i] == 0) {
sum++;
mem = i;
}
// cout<<i<<" "<<cd[i]<<endl ;
}
if (sum == 1) {
printf("%d", sccsz[mem]);
} else if (sum == 0)
printf("%d", n);
else
printf("0");
return 0;
}
C.最大半连通子图
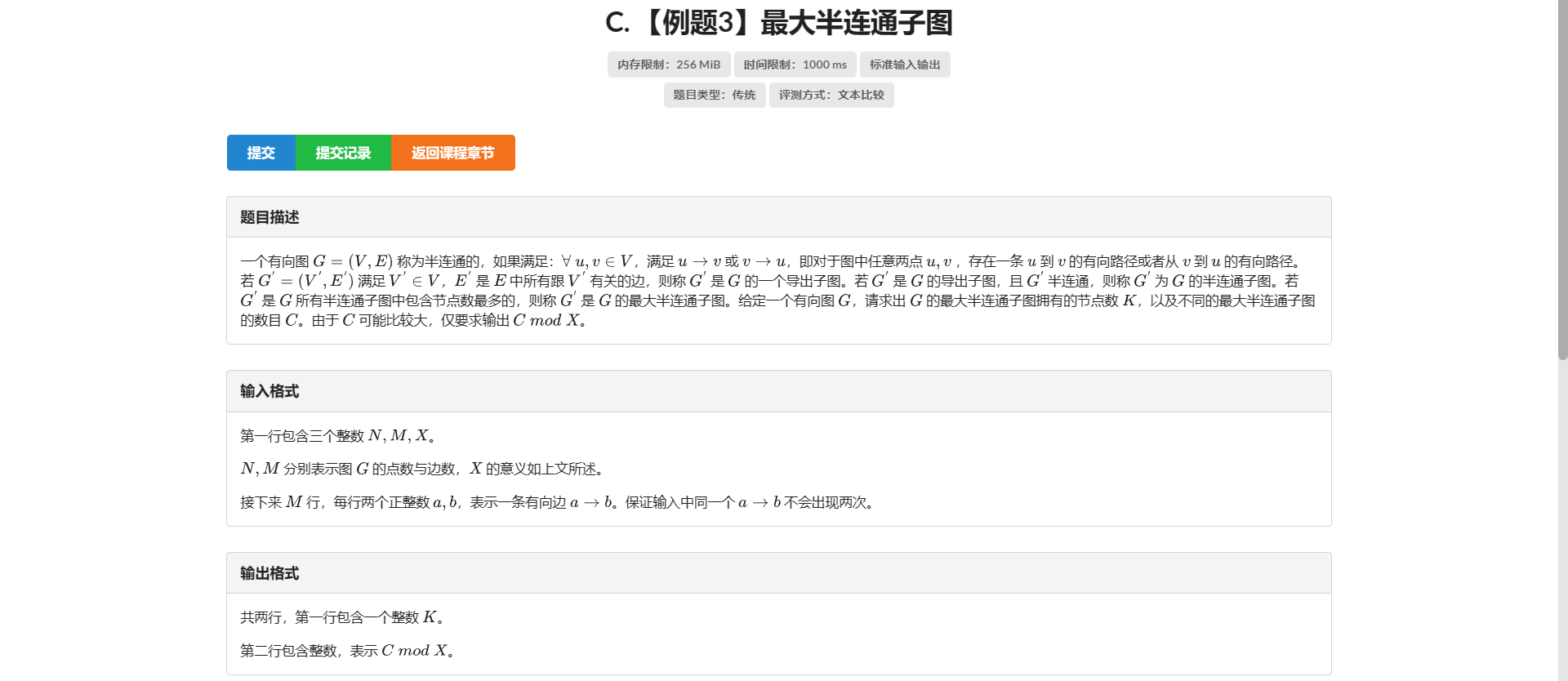
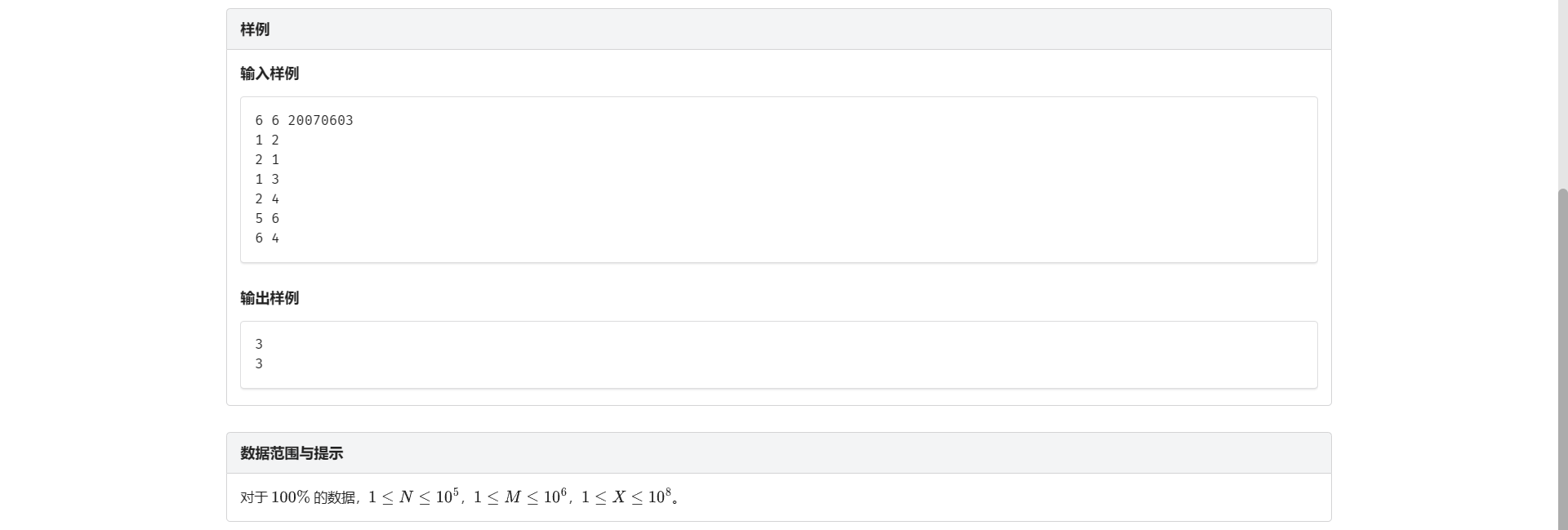
信息题 一般看到这种题都很谔谔
但是还是要硬着头皮分析一下什么意思
主要就是说 在一个半连通图中 不存在一对都无法到达的点
那长啥样的图不是一个半连通图呢
比如这样
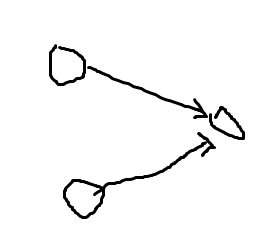
进而思考 如果这图是个 \(DAG\) 那么半连通图一定是一条链
那么我们可不可以考虑缩点呢
发现一个强连通图一定是一个半连通图 并且里面的点可以互相到达
所以缩点对于信息没有影响
然后就转化成了 \(DAG\) 上的一个 \(DP\) 了
转移式非常显然 看代码就能看懂
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 0721;
int head[N], nxt[N], to[N], cnt;
int sccnum[N], sccsz[N], dfn[N], low[N], q[N], dfs_clock, scccnt, top;
int head1[N], nxt1[N], to1[N], cnt1;
int last[N], ans[N], f[N];
int n, m, mod;
inline void cmb(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
inline void tarjan(int x) {
dfn[x] = low[x] = ++dfs_clock;
q[++top] = x;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
}
else if (!sccnum[y])
low[x] = min(low[x], dfn[y]);
}
if (low[x] == dfn[x]) {
++scccnt;
while(1) {
int now = q[top];
--top;
sccnum[now] = scccnt;
++sccsz[scccnt];
if (x == now)
break;
}
}
}
inline void cmb1(int x, int y) {
to1[++cnt1] = y;
nxt1[cnt1] = head1[x];
head1[x] = cnt1;
}
int main() {
scanf("%d%d%d", &n, &m, &mod);
for (int i = 1; i <= m; ++i) {
int x, y;
scanf("%d%d", &x, &y);
cmb(x, y);
}
for (int i = 1; i <= n; ++i) {
if (!dfn[i])
tarjan(i);
}
for (int i = 1; i <= n; ++i) {
for (int j = head[i]; j; j = nxt[j]) {
int y = to[j];
if (sccnum[y] != sccnum[i])
cmb1(sccnum[i], sccnum[y]);
}
}
for (int i = 1; i <= scccnt; ++i) {
f[i] = sccsz[i];
ans[i] = 1;
}
for (int i = scccnt; i >= 1; --i) {
for (int j = head1[i]; j; j = nxt1[j]) {
int y = to1[j];
if (i == last[y])
continue;
// cout << i << " " << y << endl;
last[y] = i;
if (f[y] < f[i] + sccsz[y]) {
f[y] = f[i] + sccsz[y];
ans[y] = ans[i];
}
else if (f[y] == f[i] + sccsz[y]) {
ans[y] += ans[i];
ans[y] %= mod;
}
// cout << i << " " << y << endl;
// cout << f[y] << " " << ans[y] << endl;
}
}
int sum = 0, tmp = 0;
for (int i = 1; i <= scccnt; ++i) {
if (sum < f[i]) {
sum = f[i];
tmp = ans[i];
}
else if(sum == f[i]) {
tmp += ans[i];
tmp %= mod;
}
}
printf("%d\n%d",sum,tmp);
return 0;
}
D.恒星的亮度
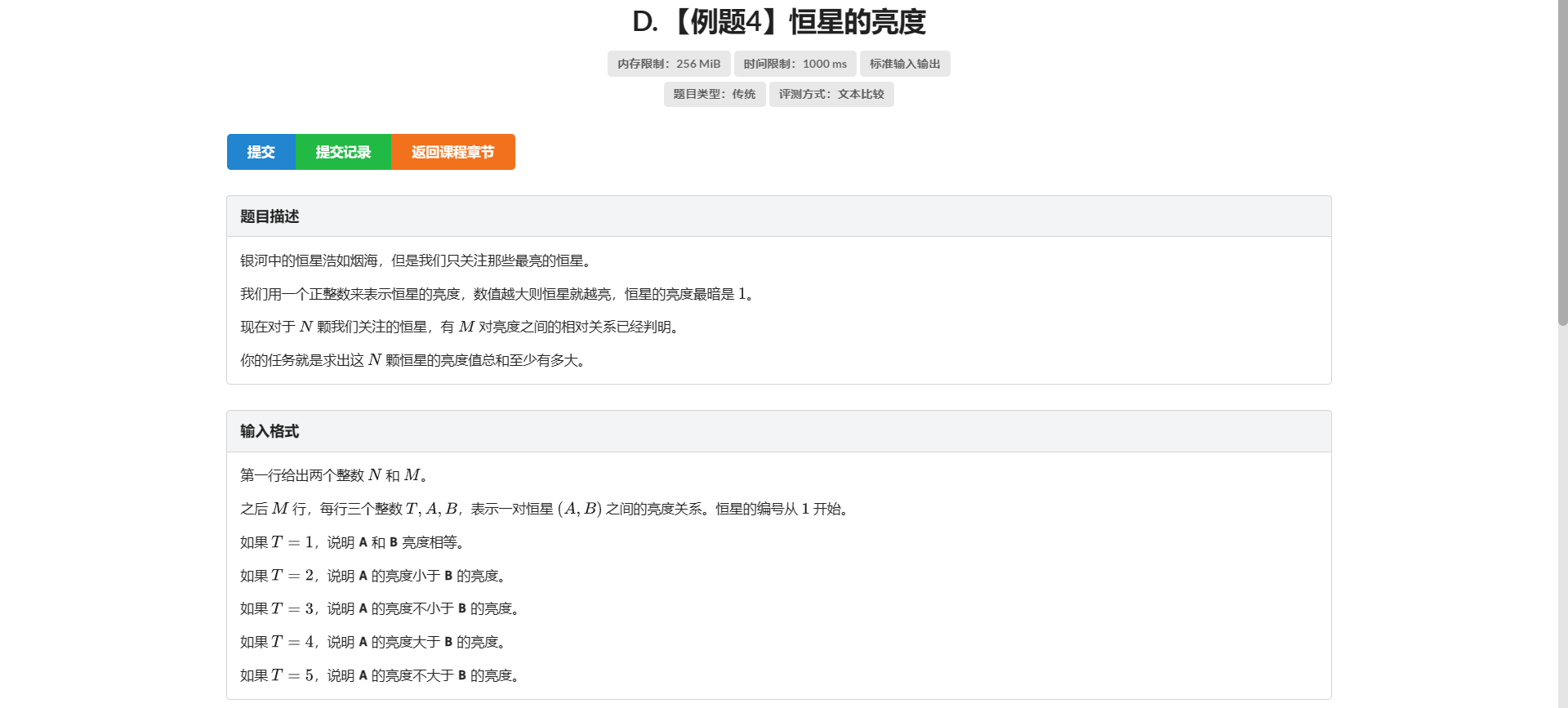
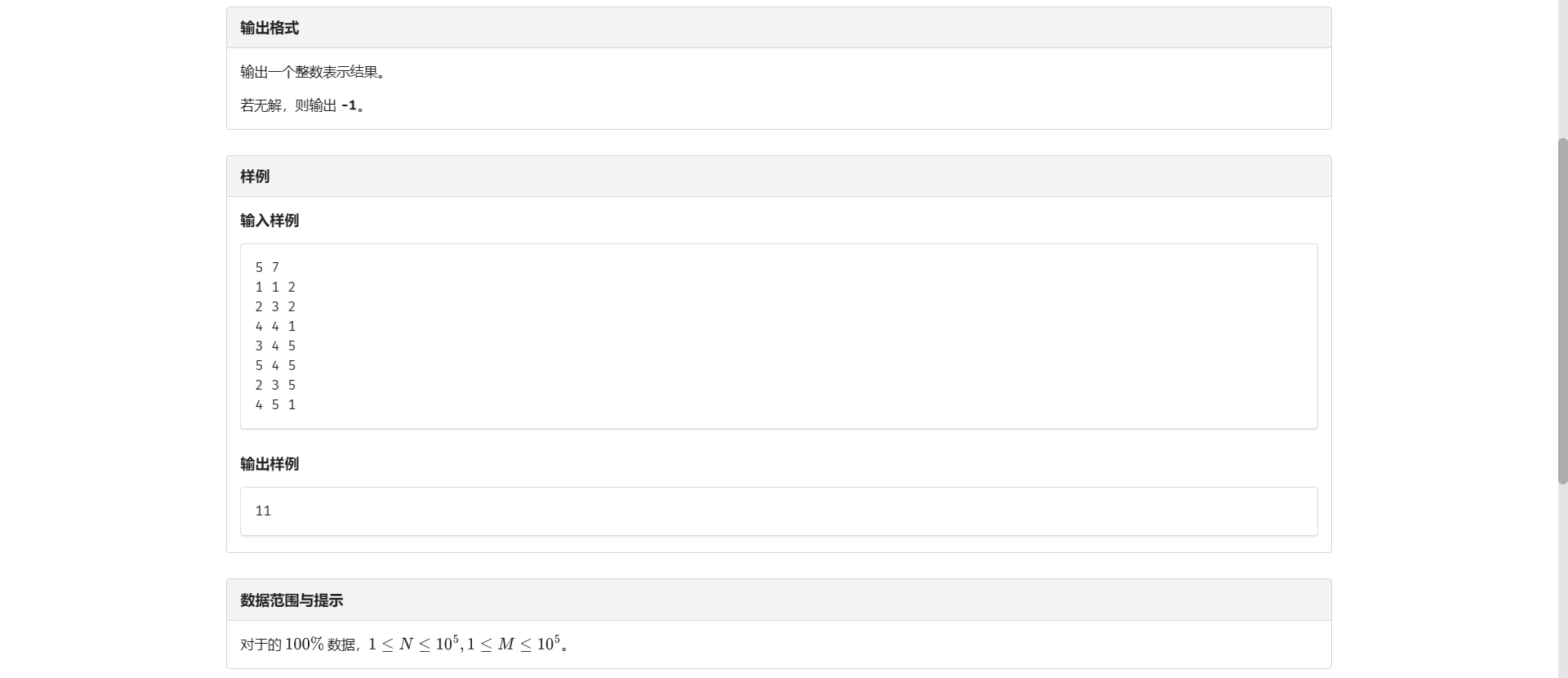
不了解差分约束的请戳差分约束学习笔记
但是这题不能跑最短路 至少理论不能
我们还是思考 这题和普通的差分约束题有什么区别
发现这题的边权只有 \(1\) \(-1\) 和 \(0\) 之分
并且我们可以通过某种方式让边权只有 \(0\) 和 \(1\)
那么假如有一条由 \(x\) 到 \(y\) 的边 就一定有 \(dis[y] \ge dis[x]\)
那么如果有解的话 当 \(x\) 与 \(y\) 强连通时 一定有 \(dis[x] = dis[y]\)
然后就是 \(Tarjan\) + \(DP\) 了
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 3e5 + 0721;
int head[N], to[N], nxt[N], len[N], cnt;
int sccnum[N], sccsz[N], sccsiz[N], dfn[N], low[N], q[N], dfs_clock, scccnt, top;
int head1[N], to1[N], nxt1[N], len1[N], cnt1;
int dis[N];
int n, m;
inline void cmb(int x, int y, int z) {
to[++cnt] = y;
len[cnt] = z;
nxt[cnt] = head[x];
head[x] = cnt;
}
inline void tarjan(int x) {
dfn[x] = low[x] = ++dfs_clock;
q[++top] = x;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (!sccnum[y]) {
low[x] = min(low[x], dfn[y]);
}
}
if (dfn[x] == low[x]) {
++scccnt;
while(1) {
int now = q[top];
--top;
sccnum[now] = scccnt;
++sccsiz[scccnt];
if (now == x)
break;
}
}
}
inline void cmb1(int x, int y, int z) {
to1[++cnt1] = y;
len1[cnt1] = z;
nxt1[cnt1] = head1[x];
head1[x] = cnt1;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int x, y, num;
scanf("%d%d%d", &num, &x, &y);
if (num == 1)
cmb(x, y, 0), cmb(y, x, 0);
else if (num == 2)
cmb(x, y, 1);
else if (num == 3)
cmb(y, x, 0);
else if (num == 4)
cmb(y, x, 1);
else
cmb(x, y, 0);
}
for(int i = 1; i <= n; ++i) cmb(0, i, 0);
tarjan(0);
for (int i = 0; i <= n; ++i) {
for (int j = head[i]; j; j = nxt[j]) {
int y = to[j];
if (sccnum[i] != sccnum[y])
cmb1(sccnum[i], sccnum[y], len[j]);
else
sccsz[sccnum[i]] += len[j];
}
}
for (int i = 1; i <= scccnt; ++i) {
if (sccsz[i] != 0) {
printf("-1");
return 0;
}
}
// cout<<"!";
ll ans = 0;
for (int i = 1; i <= scccnt; ++i)
dis[i] = 1;
for (int i = scccnt; i >= 1; --i) {
for (int j = head1[i]; j; j = nxt1[j]) {
int y = to1[j];
// cout<<y<<" "<<dis[y]<<" "<<len1[j]<<endl;
dis[y] = max(dis[y], dis[i] + len1[j]);
}
}
for (int i = 1; i < scccnt; ++i)
ans += (ll)dis[i] * sccsiz[i];
printf("%lld",ans);
return 0;
}
E.网络传输
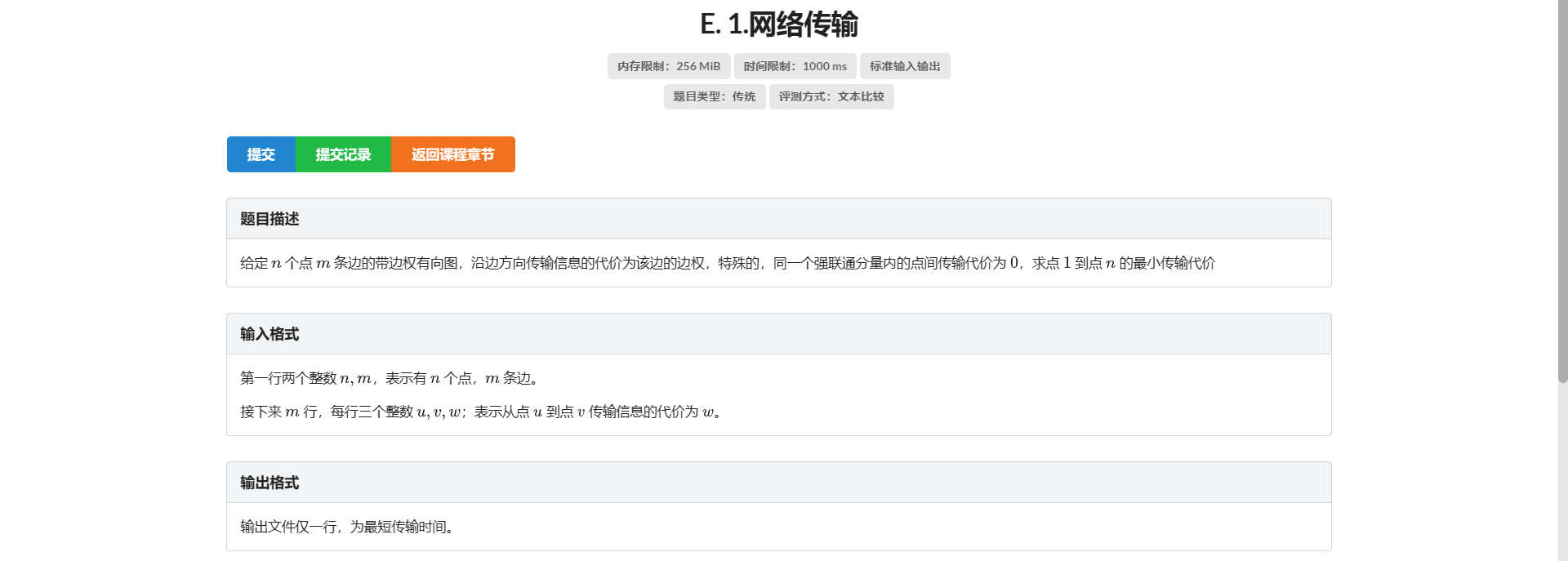
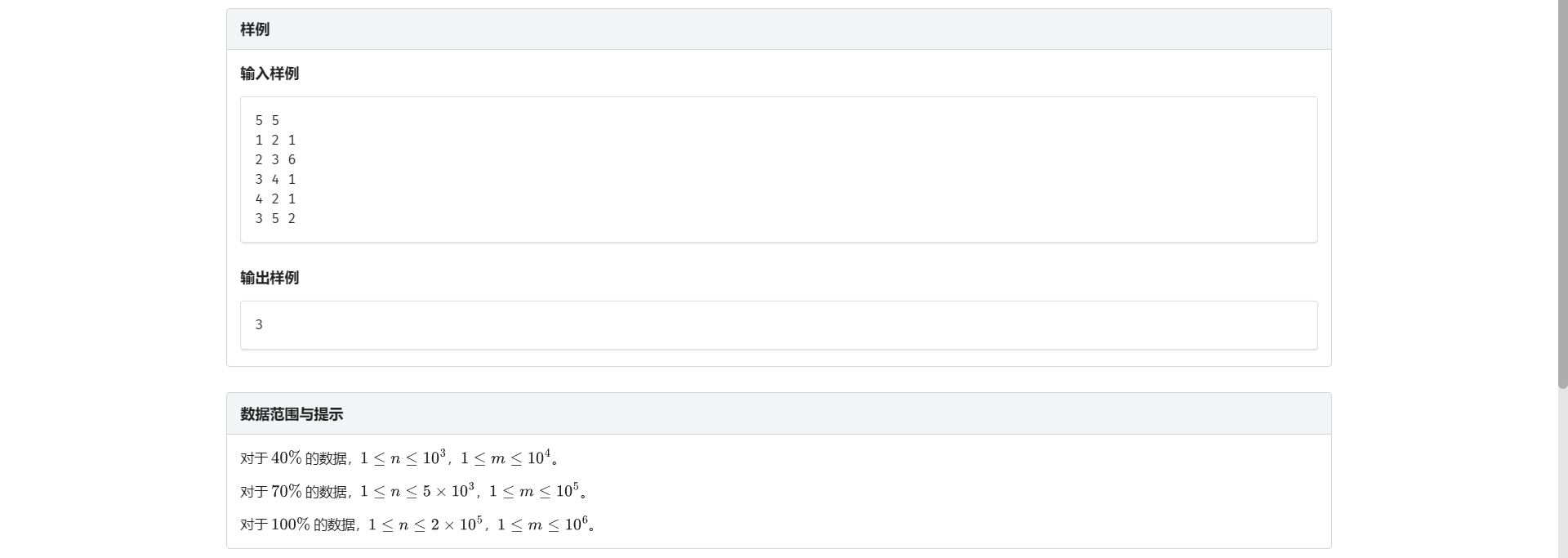
没啥好说的 缩点 DP 即可
建议封装链前 别像下面那个代码写两套系统结果忘了一个 \(\texttt_\) 修了好久
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 2e5 + 0721;
const int M = 1e6 + 0721;
int head[N], nxt[M], to[M], len[M], cnt;
int _head[N], _nxt[M], _to[M], _len[M], _cnt;
int sccnum[N], scccnt;
int dfn[N], low[N], dfs_clock;
int st[N], top;
ll f[N];
int n, m;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void add_edge(int x, int y, int z) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
len[cnt] = z;
}
inline void _add_edge(int x, int y, int z) {
// cout << x << " " << y << " " << z << "\n";
_to[++_cnt] = y;
_nxt[_cnt] = _head[x];
_head[x] = _cnt;
_len[_cnt] = z;
}
void tarjan(int x) {
dfn[x] = low[x] = ++dfs_clock;
st[++top] = x;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (!sccnum[y])
low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x]) {
++scccnt;
while (top) {
int now = st[top];
// cout << x << " " << now << "\n";
--top;
sccnum[now] = scccnt;
if (now == x) break;
}
}
}
void main() {
n = read(), m = read();
for (int i = 1; i <= m; ++i) {
int x, y, z;
x = read(), y = read(), z = read();
add_edge(x, y, z);
}
for (int i = 1; i <= n; ++i) {
if (!dfn[i]) tarjan(i);
}
for (int i = 1; i <= n; ++i) {
for (int j = head[i]; j; j = nxt[j]) {
int y = to[j];
if (sccnum[i] == sccnum[y]) continue;
_add_edge(sccnum[i], sccnum[y], len[j]);
}
}
// for (int i = 1; i <= n; ++i) cout << i << " " << sccnum[i] << "\n";
memset(f, 0x3f, sizeof f);
f[sccnum[1]] = 0;
for (int i = scccnt; i >= 1; --i) {
for (int j = _head[i]; j; j = _nxt[j]) {
int y = _to[j];
// cout << y << " " << f[i] << " " << f[y] << " " << _len[j] << "\n";
f[y] = min(f[y], f[i] + _len[j]);
}
}
printf("%lld\n", f[sccnum[n]]);
}
}
int main() {
steven24::main();
return 0;
}
/*
5 5
1 2 1
2 3 6
3 4 1
4 2 1
3 5 2
*/
F.通讯问题
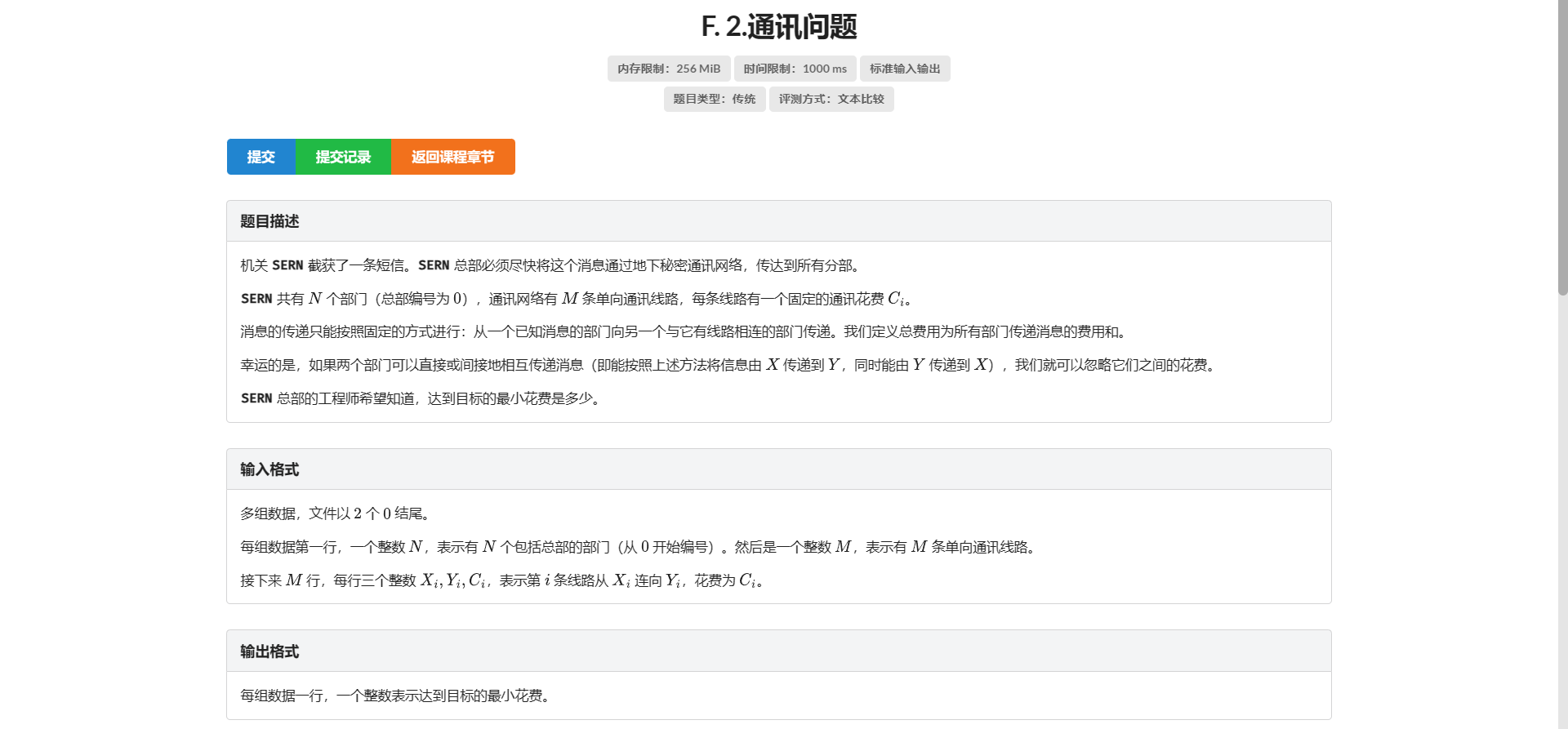
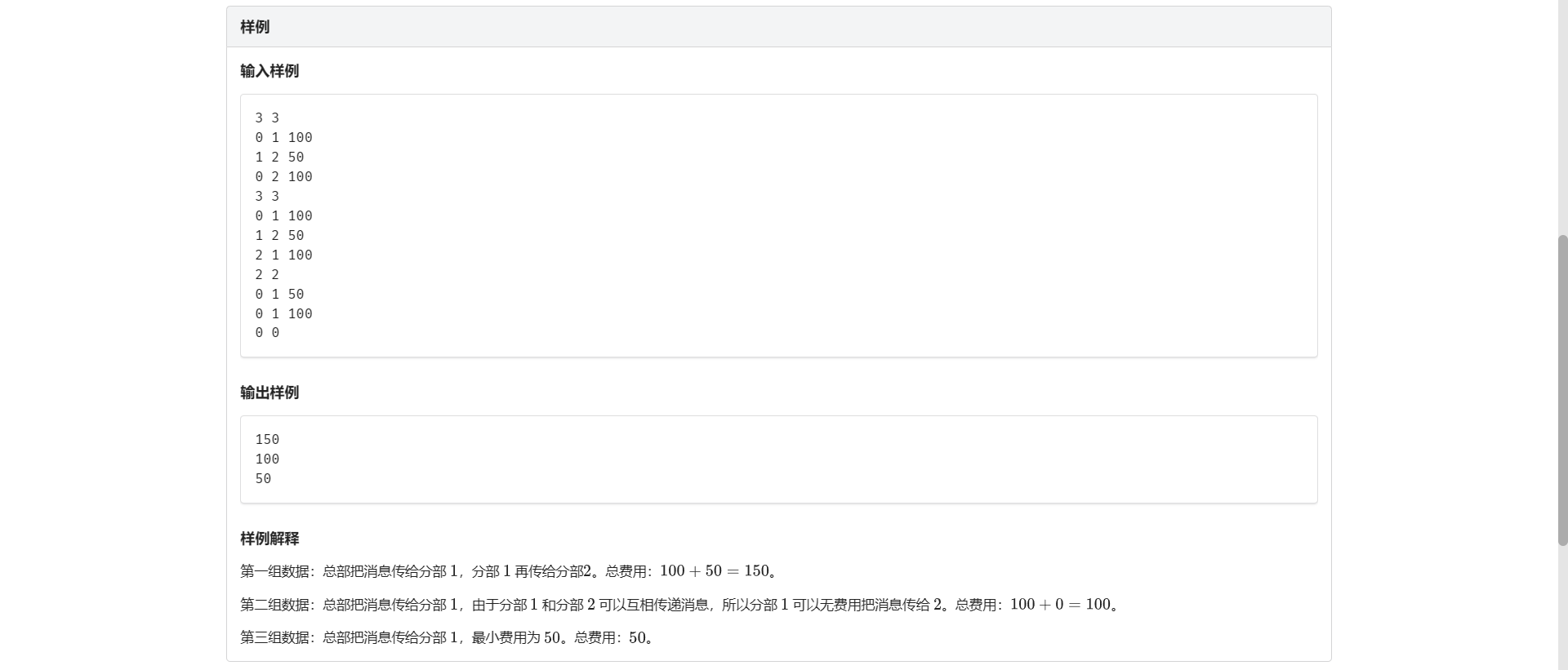

这题没做出来 啥啊。。
考虑记录前置状态 假了
考虑 bfs 假了
考虑最小费用最大流 不知道假没假但是狗都不写
题解:贪心的选能到达它的最小的边
我:6
结果多测写了 init 函数主函数没调用 蠢到家了。
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 2e5 + 0721;
const int M = 1e6 + 0721;
int head[N], nxt[M], to[M], len[M], cnt;
int _head[N], _nxt[M], _to[M], _len[M], _cnt;
int sccnum[N], scccnt;
int dfn[N], low[N], dfs_clock;
int st[N], top;
ll f[N];
int n, m;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
void init() {
memset(head, 0, sizeof head);
memset(_head, 0, sizeof _head);
memset(dfn, 0, sizeof dfn);
memset(low, 0, sizeof low);
memset(sccnum, 0, sizeof sccnum);
cnt = _cnt = top = 0;
scccnt = dfs_clock = 0;
}
inline void add_edge(int x, int y, int z) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
len[cnt] = z;
}
inline void _add_edge(int x, int y, int z) {
_to[++_cnt] = y;
_nxt[_cnt] = _head[x];
_head[x] = _cnt;
_len[_cnt] = z;
}
void tarjan(int x) {
dfn[x] = low[x] = ++dfs_clock;
st[++top] = x;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (!sccnum[y])
low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x]) {
++scccnt;
while (top) {
int now = st[top];
--top;
sccnum[now] = scccnt;
if (now == x) break;
}
}
}
void main() {
while (1) {
n = read(), m = read();
init();
if (n == 0 && m == 0) break;
for (int i = 1; i <= m; ++i) {
int x, y, z;
x = read(), y = read(), z = read();
++x, ++y;
add_edge(x, y, z);
}
for (int i = 1; i <= n; ++i) {
if (!dfn[i]) tarjan(i);
}
for (int i = 1; i <= n; ++i) {
for (int j = head[i]; j; j = nxt[j]) {
int y = to[j];
if (sccnum[i] == sccnum[y]) continue;
_add_edge(sccnum[i], sccnum[y], len[j]);
}
}
// for (int i = 1; i <= n; ++i) cout << i << " " << sccnum[i] << "\n";
memset(f, 0x3f, sizeof f);
f[sccnum[1]] = 0;
for (int i = scccnt; i >= 1; --i) {
for (int j = _head[i]; j; j = _nxt[j]) {
int y = _to[j];
f[y] = min(f[y], (ll)_len[j]);
}
}
// for (int i = 1; i <= n; ++i) cout << i << " " << pre[i] << " " << f[i] << "\n";
ll ans = 0;
for (int i = 1; i <= scccnt; ++i) ans += f[i];
printf("%lld\n", ans);
}
}
}
int main() {
steven24::main();
return 0;
}
/*
3 3
0 1 100
1 2 50
0 2 100
3 3
0 1 100
1 2 50
2 1 100
2 2
0 1 50
0 1 100
0 0
*/
G.删点次数
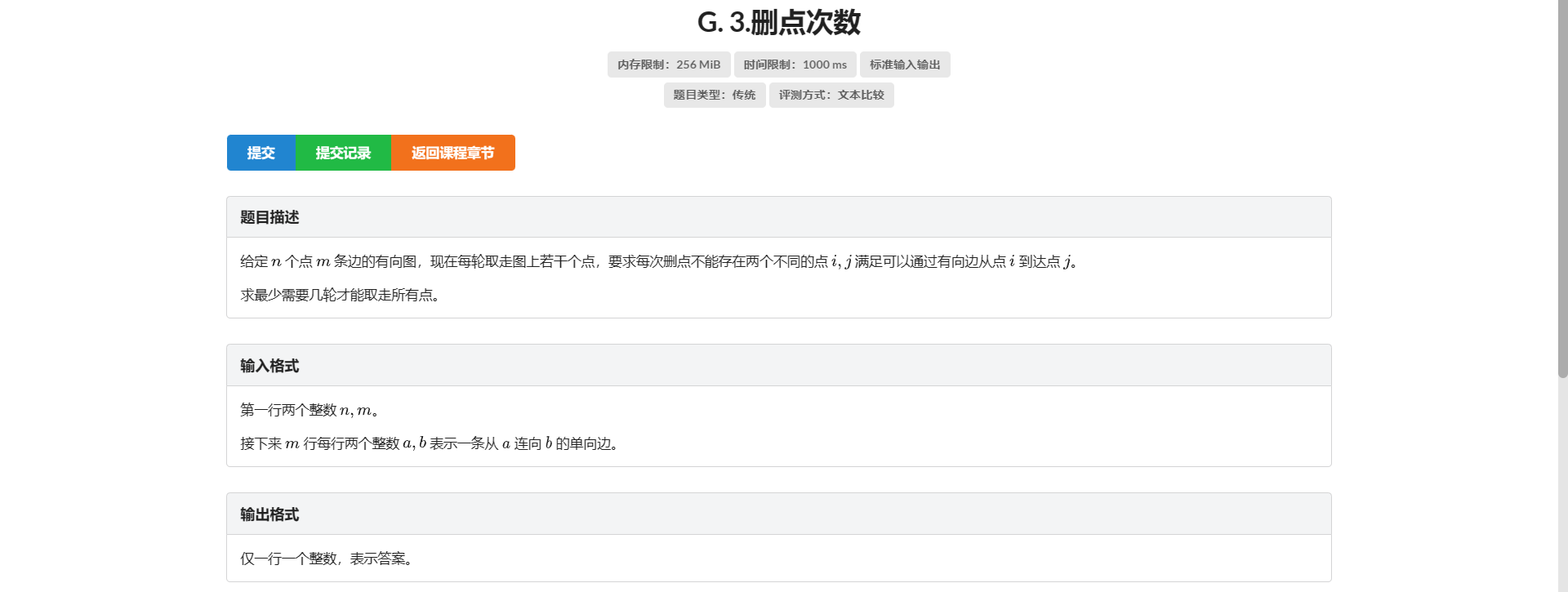
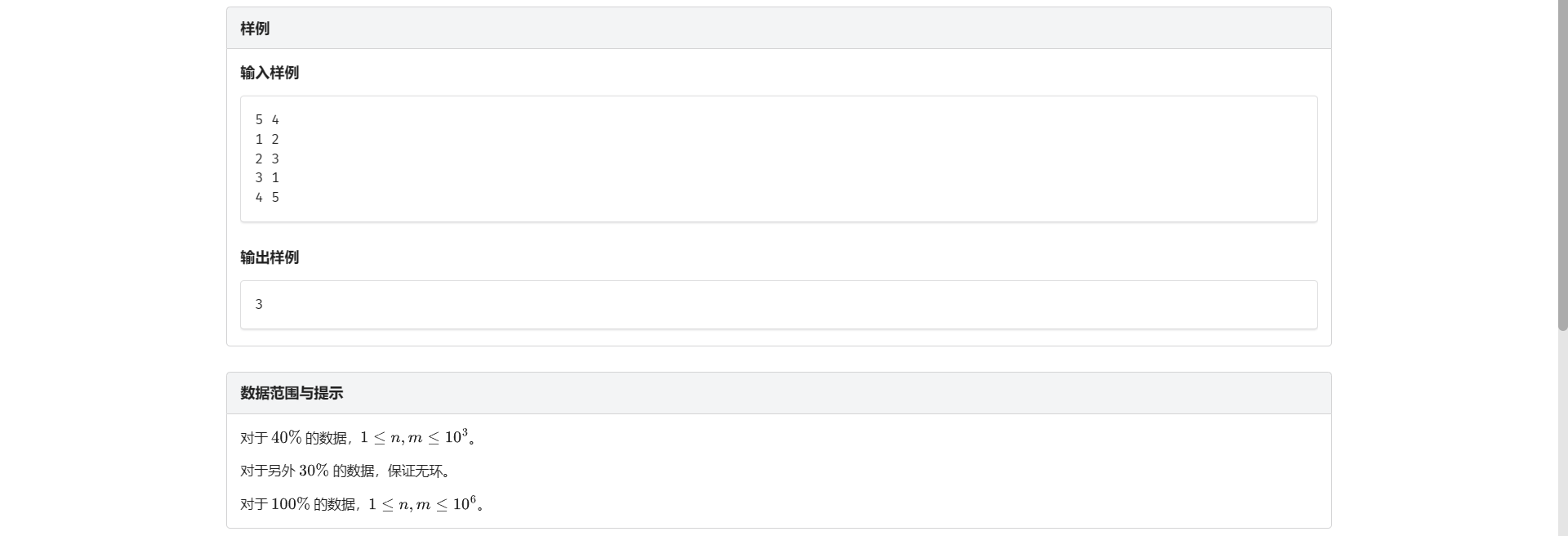
首先看到部分分 考虑 DAG 的情况
发现实际上就是最长链的长度
那么对于一个强连通分量 我们盲猜需要删的次数就为它的大小
一点碎碎念:
3 4
1 2
2 1
2 3
3 2
答案应为 2 但是 AC 程序输出 3
猜想 std 应该也是有问题的 总是要么是这做法假了要么真是这题有问题(
但是如果指的是每次删的点在原图中不能互相到达似乎就说的通了(?
那看来还是我理解问题
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 1e6 + 0721;
int dfn[N], low[N], dfs_clock;
int sccnum[N], sccsz[N], scccnt;
int st[N], top;
int f[N];
int n, m;
struct graph {
int head[N], nxt[N], to[N], cnt;
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
};
graph G1, G2;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
void tarjan(int x) {
dfn[x] = low[x] = ++dfs_clock;
st[++top] = x;
for (int i = G1.head[x]; i; i = G1.nxt[i]) {
int y = G1.to[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (!sccnum[y])
low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x]) {
++scccnt;
while (1) {
int now = st[top];
--top;
sccnum[now] = scccnt;
++sccsz[scccnt];
if (now == x) break;
}
}
}
void main() {
n = read(), m = read();
for (int i = 1; i <= m; ++i) {
int x, y;
x = read(), y = read();
G1.add_edge(x, y);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i) {
for (int j = G1.head[i]; j; j = G1.nxt[j]) {
int y = G1.to[j];
if (sccnum[y] == sccnum[i]) continue;
G2.add_edge(sccnum[i], sccnum[y]);
}
}
for (int i = 1; i <= scccnt; ++i) f[i] = sccsz[i];
for (int i = scccnt; i >= 1; --i) {
for (int j = G2.head[i]; j; j = G2.nxt[j]) {
int y = G2.to[j];
f[y] = max(f[y], f[i] + sccsz[y]);
}
}
int ans = 0;
for (int i = 1; i <= scccnt; ++i) ans = max(ans, f[i]);
printf("%d\n", ans);
}
}
int main() {
steven24::main();
return 0;
}
/*
5 4
1 2
2 3
3 1
4 5
*/
H.软件安装
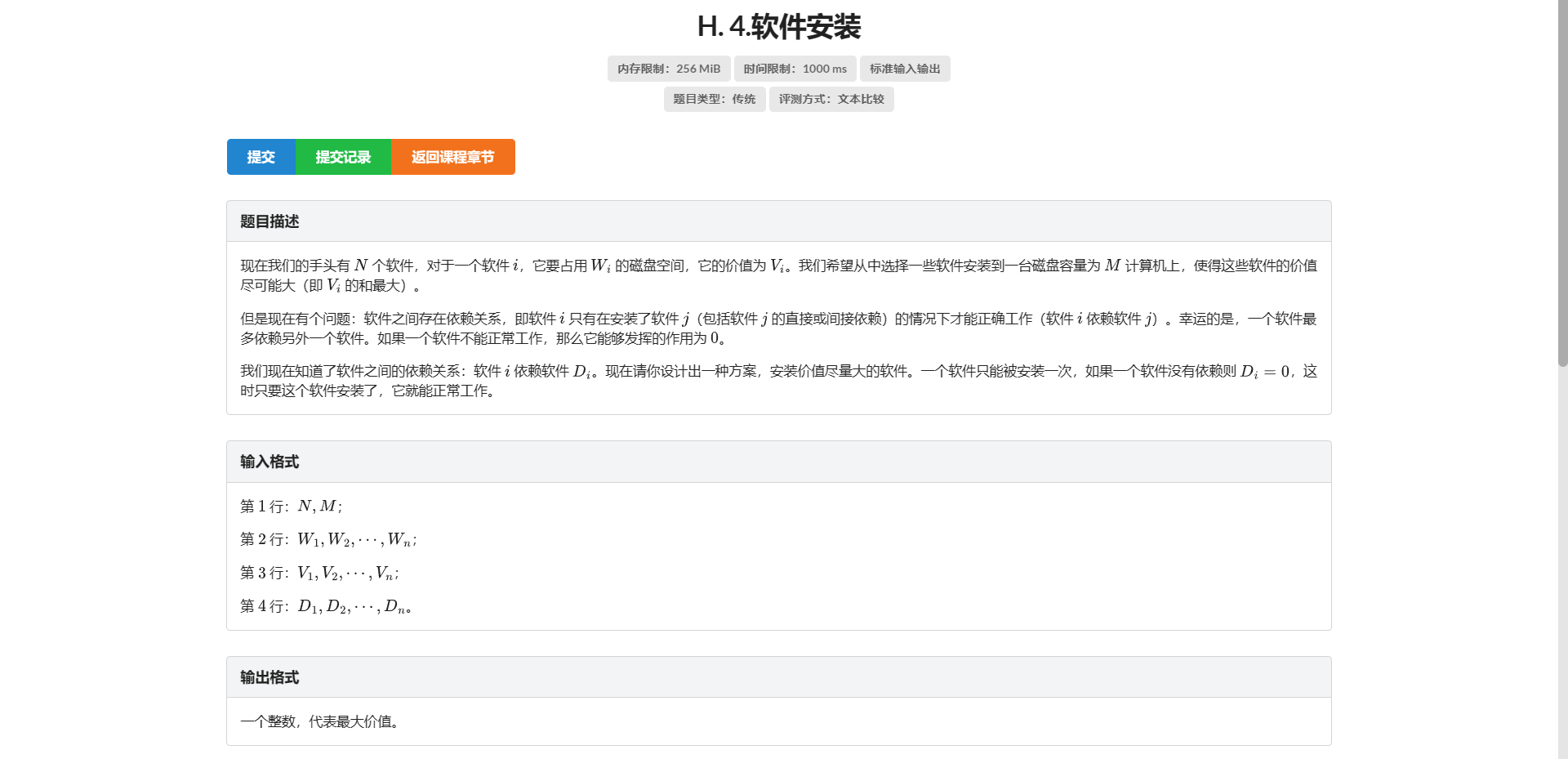
树上背包
考虑有可能互相依赖 所以要缩点
-
注意全缩完之后判入度再连 0
-
注意树上背包外层循环倒序枚举
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define int long long
using namespace std;
namespace steven24 {
const int N = 521;
int dfn[N], low[N], dfs_clock;
int sccnum[N], sccw[N], sccv[N], scccnt;
int st[N], top;
ll f[N][N]; // 第i个点 重量为j时的最大价值
int w[N], v[N], d[N];
int rd[N];
int n, m;
struct graph {
int head[N], nxt[N], to[N], cnt;
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
};
graph G1, G2;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
void tarjan(int x) {
dfn[x] = low[x] = ++dfs_clock;
st[++top] = x;
for (int i = G1.head[x]; i; i = G1.nxt[i]) {
int y = G1.to[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (!sccnum[y])
low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x]) {
++scccnt;
while (1) {
int now = st[top];
--top;
sccnum[now] = scccnt;
sccw[scccnt] += w[now];
sccv[scccnt] += v[now];
if (now == x) break;
}
}
}
void dfs(int x) {
for (int i = sccw[x]; i <= m; ++i) f[x][i] = sccv[x];
for (int i = G2.head[x]; i; i = G2.nxt[i]) {
int y = G2.to[i];
dfs(y);
for (int j = m - sccw[x]; j >= 0; --j) {
for (int k = 0; k <= j; ++k) {
f[x][j + sccw[x]] = max(f[x][j + sccw[x]], f[y][k] + f[x][j + sccw[x] - k]);
}
}
}
}
void main() {
n = read(), m = read();
for (int i = 1; i <= n; ++i) w[i] = read();
for (int i = 1; i <= n; ++i) v[i] = read();
for (int i = 1; i <= n; ++i) d[i] = read();
for (int i = 1; i <= n; ++i) if (d[i]) G1.add_edge(d[i], i);
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i) {
for (int j = G1.head[i]; j; j = G1.nxt[j]) {
int y = G1.to[j];
if (sccnum[y] == sccnum[i]) continue;
G2.add_edge(sccnum[i], sccnum[y]);
++rd[sccnum[y]];
}
}
for (int i = 1; i <= scccnt; ++i) if (!rd[i]) G2.add_edge(0, i);
dfs(0);
printf("%lld\n", f[0][m]);
}
}
signed main() {
steven24::main();
return 0;
}
/*
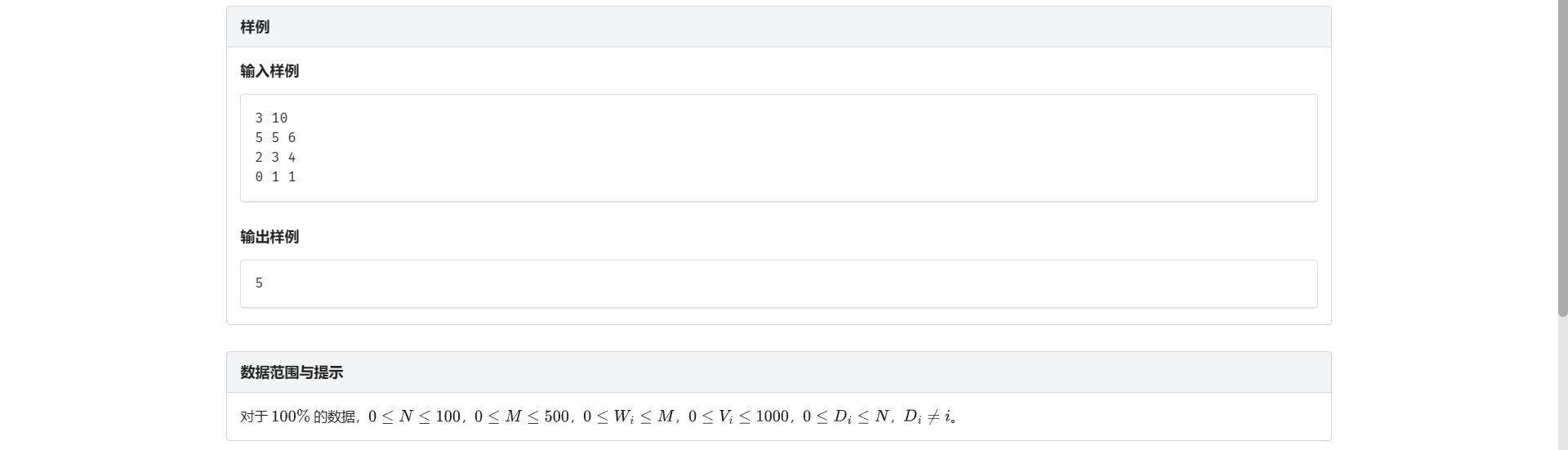
3 10
5 5 6
2 3 4
0 1 1
*/
I.宫室宝藏
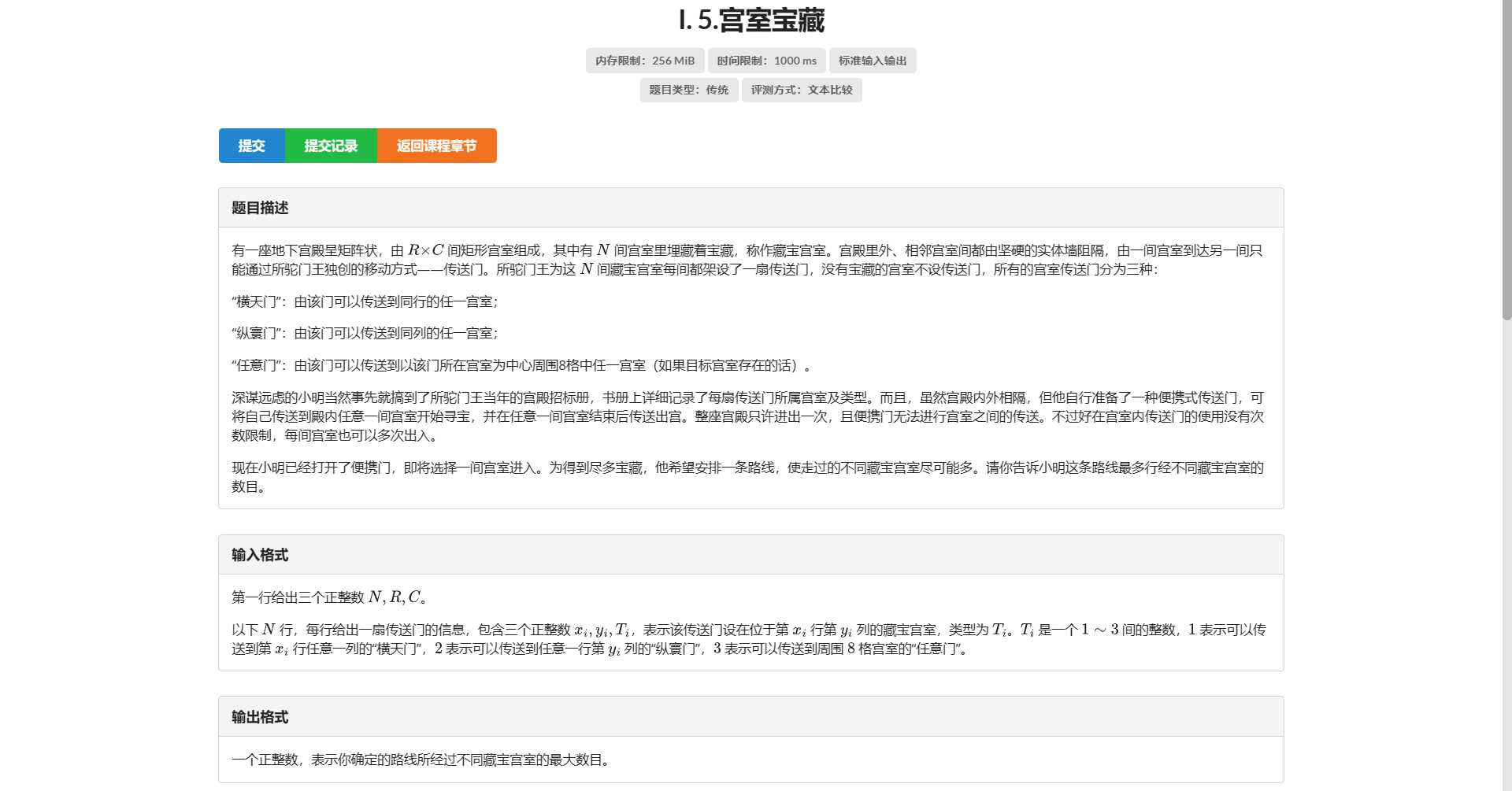
这题在 lg 竟然是个紫题。。。
主要问题在于建图
考虑同一行有横行传送门的点 我们显然不能把每两个点间都连一条边 这样是 \(n ^ 2\) 的
但是我们发现如果 \(1, 2\) 联通并且 \(2, 3\) 那么一定有 \(1,3\) 联通
所以我们把相邻的两条边联通就可以了
那么对于在这一行但是没有横行传送门的点 选取任意一个在这一行并且有横行传送门的点 连一条单向边即可
竖列同理
对于九宫格 因为最多只有 \(8\) 条单向边 暴力查即可
注意 \(R \times C \le 10^{12}\) 先压成一维再查
连完边就直接缩点求最长链即可 可以连超级源点和超级汇点方便统计答案
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 1e6 + 0721;
int dfn[N], low[N], dfs_clock;
int sccnum[N], sccsz[N], scccnt;
int st[N], top;
int f[N];
int dx[8] = {1, 1, 1, 0, 0, -1, -1, -1};
int dy[8] = {1, 0, -1, 1, -1, -1, 1, 0};
vector<int> h[N], l[N];
map<ll, int> vis;
int n, R, C;
struct graph {
int head[N], nxt[N], to[N], cnt;
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
};
graph G1, G2;
struct treasure {
int x, y, id, opt;
} a[N];
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline ll change(int x, int y) {
return 1ll * (x - 1) * C + y;
}
void connect (int x, int y, int id) {
for (int i = 0; i < 8; ++i) {
int tx = x + dx[i], ty = y + dy[i];
if (tx < 1 || tx > R || ty < 1 || ty > C) continue;
if (vis.find(change(tx, ty)) != vis.end()) G1.add_edge(id, vis[change(tx, ty)]);
}
}
void tarjan(int x) {
dfn[x] = low[x] = ++dfs_clock;
st[++top] = x;
for (int i = G1.head[x]; i; i = G1.nxt[i]) {
int y = G1.to[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (!sccnum[y])
low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x]) {
++scccnt;
while (1) {
int now = st[top];
--top;
sccnum[now] = scccnt;
++sccsz[scccnt];
if (now == x) break;
}
}
}
void main() {
n = read(), R = read(), C = read();
for (int i = 1; i <= n; ++i) {
a[i].x = read(), a[i].y = read(), a[i].opt = read();
a[i].id = i;
switch (a[i].opt) {
case 1 : {
h[a[i].x].push_back(i);
break;
}
case 2 : {
l[a[i].y].push_back(i);
break;
}
default : {
break;
}
}
vis[change(a[i].x, a[i].y)] = i;
}
for (int i = 1; i <= R; ++i) {
if (!h[i].size()) continue;
for (int j = 0; j < (int)h[i].size() - 1; ++j) {
G1.add_edge(h[i][j], h[i][j + 1]);
G1.add_edge(h[i][j + 1], h[i][j]);
}
}
for (int i = 1; i <= C; ++i) {
if (!l[i].size()) continue;
for (int j = 0; j < (int)l[i].size() - 1; ++j ) {
G1.add_edge(l[i][j], l[i][j + 1]);
G1.add_edge(l[i][j + 1], l[i][j]);
}
}
for (int i = 1; i <= n; ++i) {
int x = a[i].x, y = a[i].y, opt = a[i].opt;
switch (opt) {
case 1 : {
if (l[y].size()) G1.add_edge(l[y][0], i);
break;
}
case 2 : {
if (h[x].size()) G1.add_edge(h[x][0], i);
break;
}
default : {
if (l[y].size()) G1.add_edge(l[y][0], i);
if (h[x].size()) G1.add_edge(h[x][0], i);
break;
}
}
}
for (int i = 1 ;i <= n; ++i) {
if (a[i].opt != 3) continue;
connect(a[i].x, a[i].y, i);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i) {
for (int j = G1.head[i]; j; j = G1.nxt[j]) {
int y = G1.to[j];
if (sccnum[y] == sccnum[i]) continue;
G2.add_edge(sccnum[i], sccnum[y]);
}
}
for (int i = 1; i <= scccnt; ++i) f[i] = sccsz[i];
for (int i = 1; i <= n; ++i) {
G2.add_edge(scccnt + 1, i);
G2.add_edge(i, 0);
}
for (int i = scccnt + 1; i >= 0; --i) {
for (int j = G2.head[i]; j; j = G2.nxt[j]) {
int y = G2.to[j];
f[y] = max(f[y], f[i] + sccsz[y]);
}
}
printf("%d\n", f[0]);
}
}
int main() {
steven24::main();
return 0;
}
/*
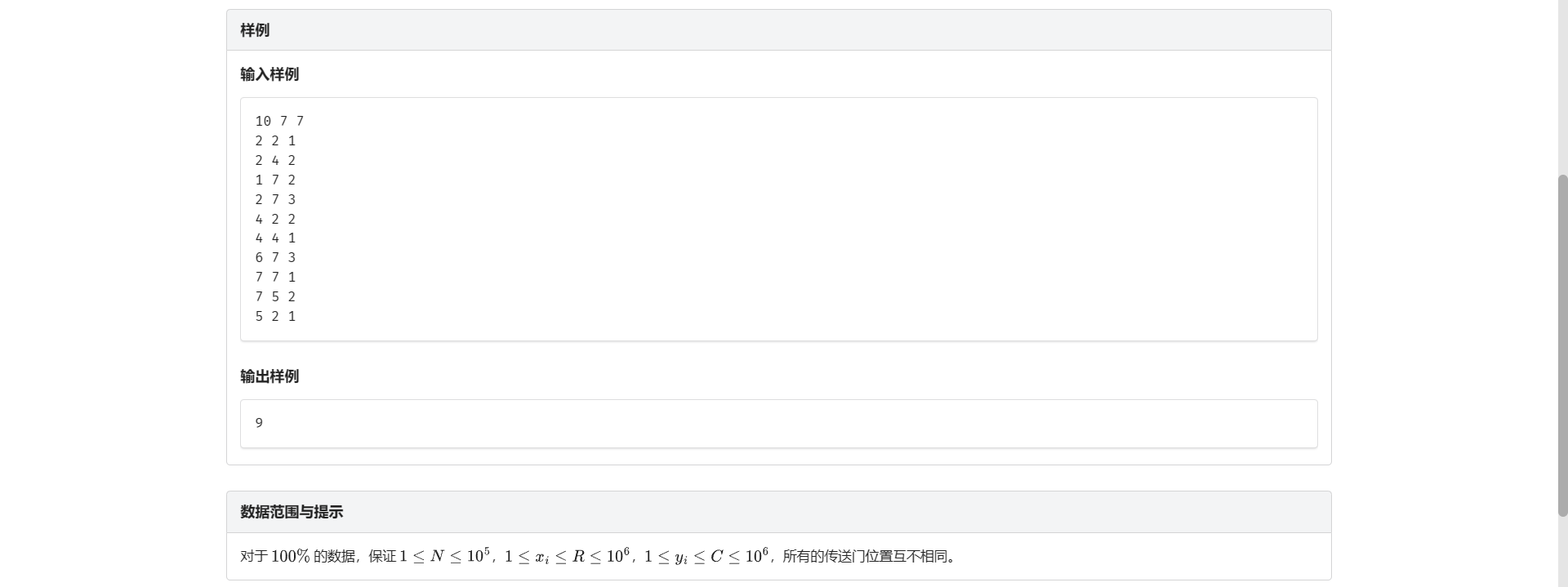
10 7 7
2 2 1
2 4 2
1 7 2
2 7 3
4 2 2
4 4 1
6 7 3
7 7 1
7 5 2
5 2 1
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号