YBTOJ 3.3最短路径
A.单源最短路径
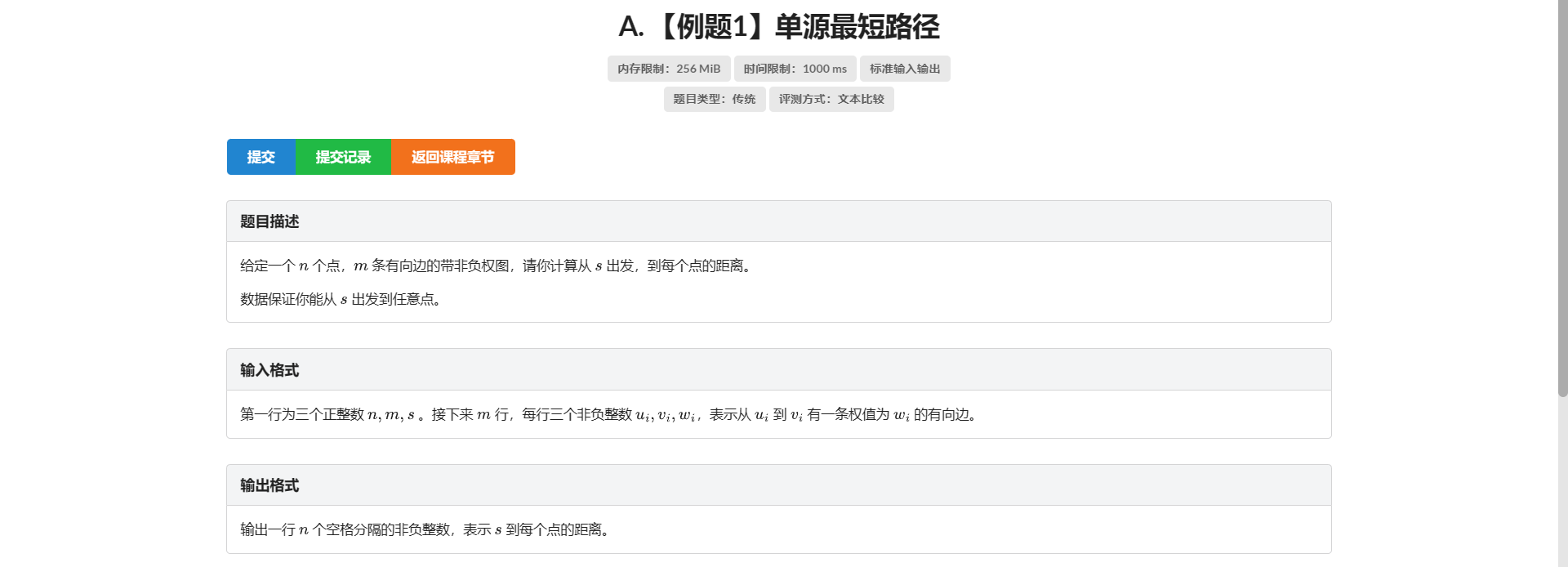
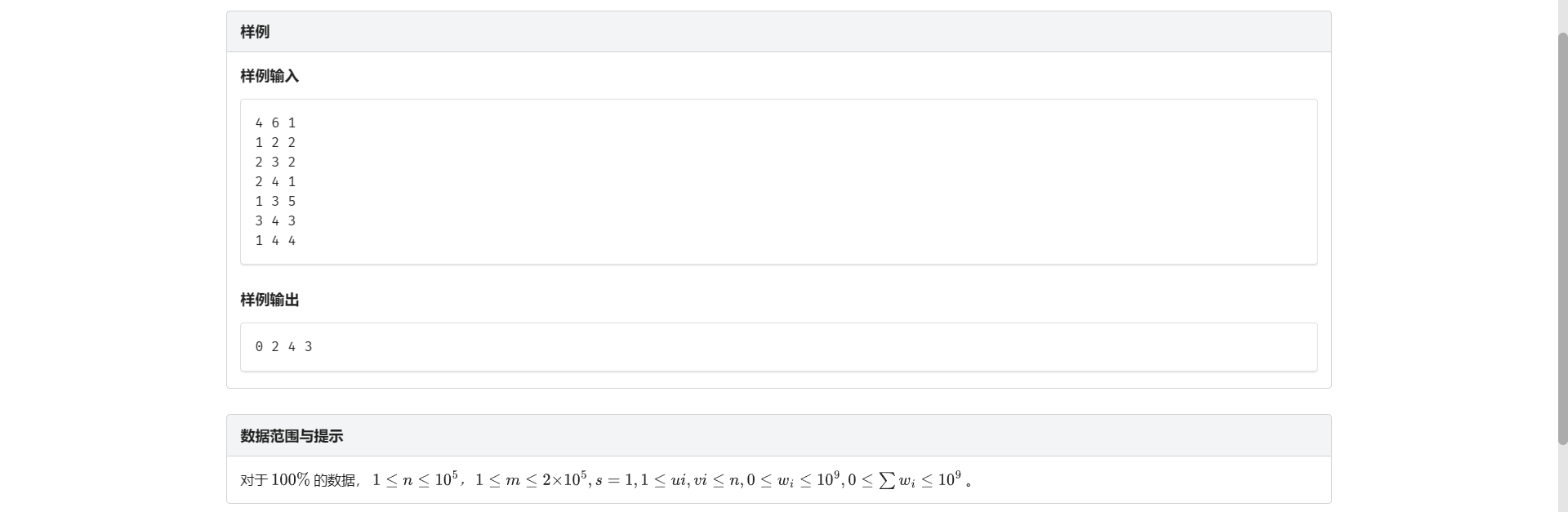
板子 没啥好说的
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 0721;
int head[N], to[N], nxt[N], len[N], cnt;
bool vis[N];
int dis[N];
int n, m, s;
void cmb(int x, int y, int z) {
to[++cnt] = y;
len[cnt] = z;
nxt[cnt] = head[x];
head[x] = cnt;
}
struct node {
int id, dis;
friend bool operator<(node a, node b) { return a.dis > b.dis; }
};
priority_queue<node> q;
void dijkstra(int s) {
memset(dis, 0x3f, sizeof(dis));
q.push((node){ s, 0 });
dis[s] = 0;
while (!q.empty()) {
int now = q.top().id;
q.pop();
if (vis[now]) continue;
vis[now] = 1;
for (int i = head[now]; i; i = nxt[i]) {
int y = to[i];
if (dis[y] > dis[now] + len[i]) {
dis[y] = dis[now] + len[i];
q.push((node){ y, dis[y] });
}
}
}
}
int main() {
scanf("%d%d%d",&n,&m,&s);
for (int i = 1; i <= m; ++i) {
int u, v, w;
scanf("%d%d%d",&u,&v,&w);
cmb(u, v, w);
}
dijkstra(s);
for (int i = 1; i <= n; ++i) printf("%d ",dis[i]);
return 0;
}
B.负环判断
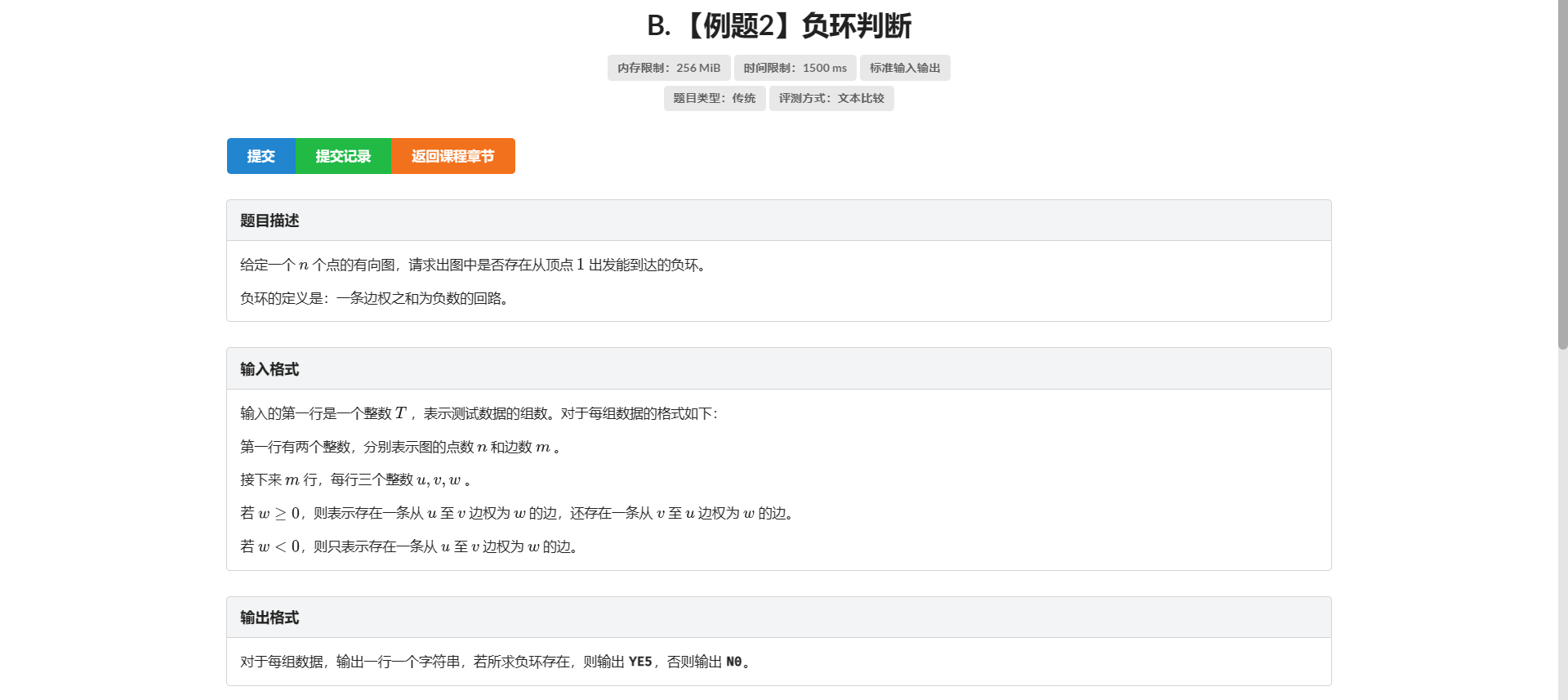
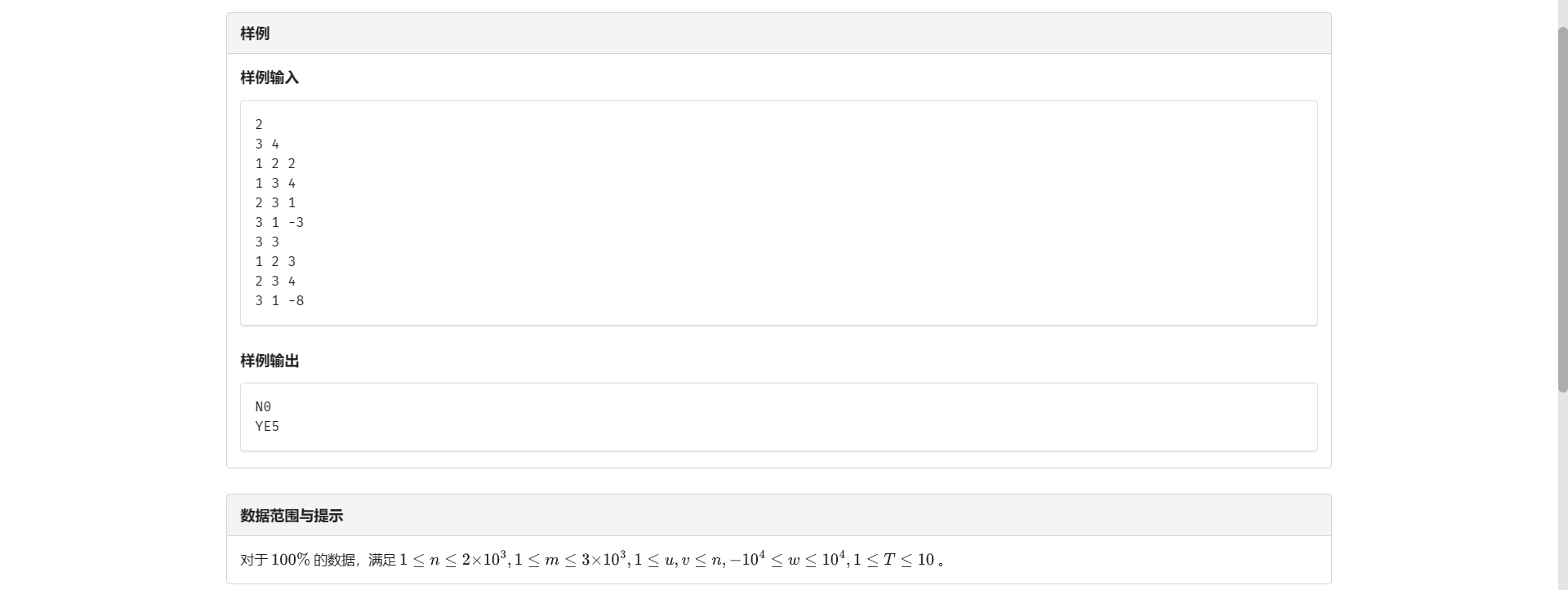
这里推荐 \(Bellman-ford\) :n次对所有点进行松弛操作 若最后一次还有点可以被松弛 就证明有负环存在
code:
bool bellman_ford(int s) {
memset(dis, 0x3f, sizeof dis );
dis[s] = 0;
bool flag;
for (int i = 1; i <= n; ++i) {
flag = 0;
for (int j = 1; j <= n; ++j) {
for (int k = head[j]; k; k = nxt[k]) {
int y = to[k];
if (dis[y] > dis[j] + len[k]) {
dis[y] = dis[j] + len[k];
flag = 1;
}
}
}
if (flag == 0) break;
}
return flag;
}
当然 \(SPFA\) 也是行的 注意要判松弛次数而不是入队次数
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
int head[N], to[N], nxt[N], len[N], cnt;
int dis[N], vis[N];
bool exist[N];
int T, m, n;
queue<int> q;
void cmb(int x, int y, int z) {
to[++cnt] = y;
len[cnt] = z;
nxt[cnt] = head[x];
head[x] = cnt;
}
bool spfa(int s) {
dis[s] = 0;
q.push(s);
exist[s] = 1;
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = head[now]; i; i = nxt[i]) {
int y = to[i];
if (dis[y] > dis[now] + len[i]) {
dis[y] = dis[now] + len[i];
if (!exist[y]) {
q.push(y);
exist[y] = 1;
}
vis[y] = vis[now] + 1;
if (vis[y] >= n)
return 1;
}
}
exist[now] = 0;
}
return 0;
}
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &m);
memset(dis, 0x3f, sizeof(dis));
memset(head, 0, sizeof(head));
memset(exist, 0, sizeof(exist));
memset(vis, 0, sizeof(vis));
for (int i = 1; i <= m; ++i) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
if (z >= 0) {
cmb(x, y, z);
cmb(y, x, z);
}
else
cmb(x, y, z);
}
if (spfa(1))
printf("YE5\n");
else
printf("N0\n");
}
return 0;
}
C.最优贸易
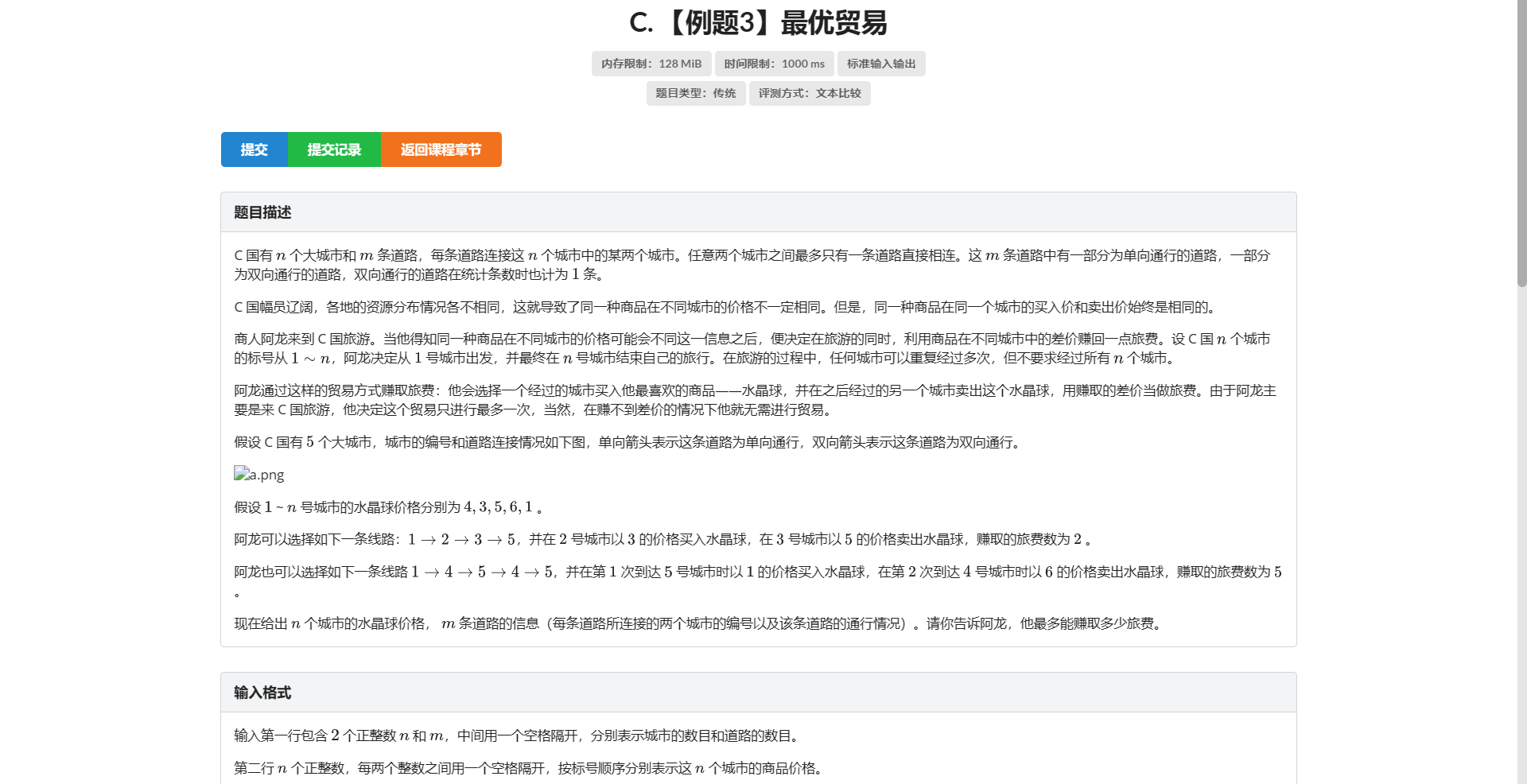
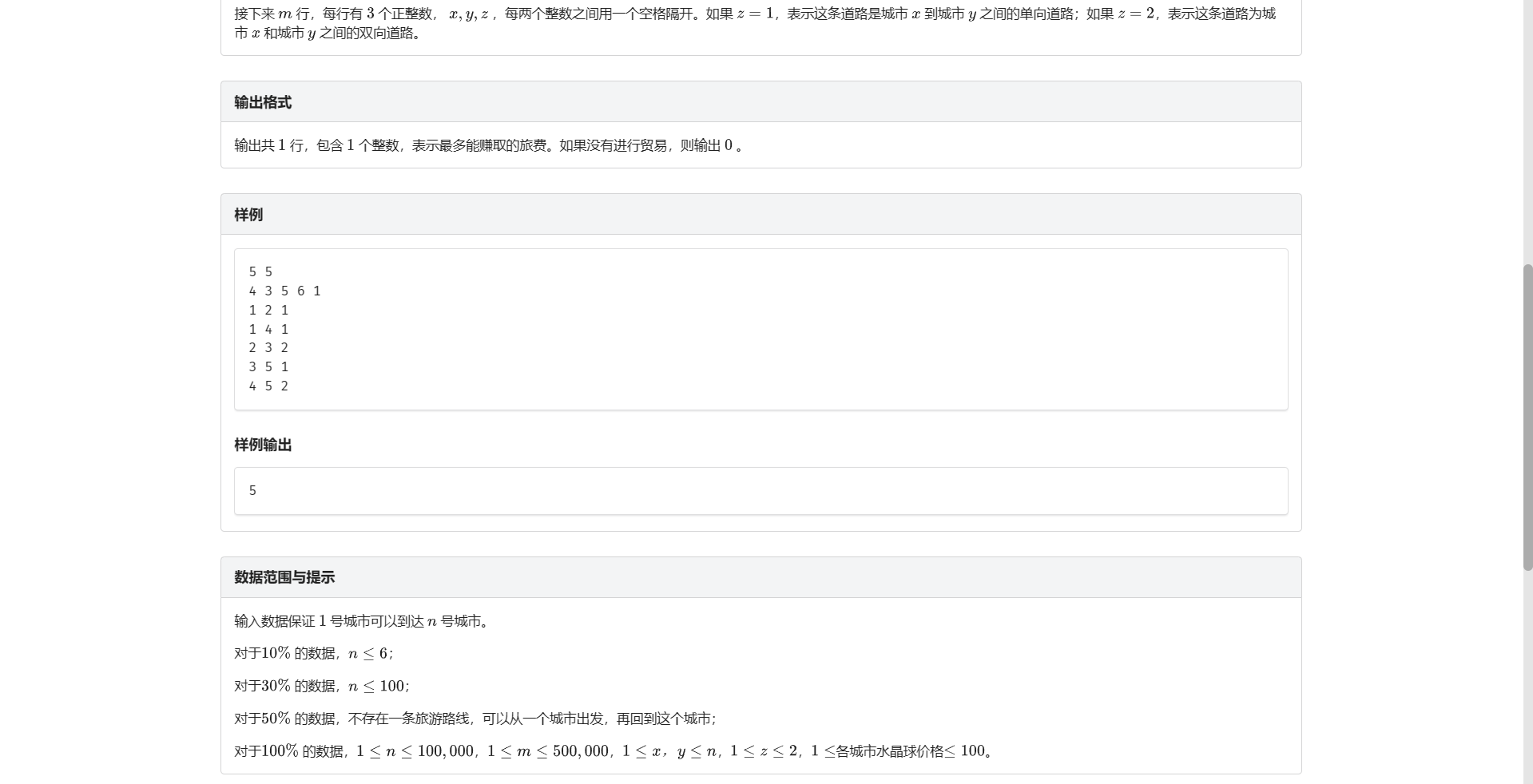
首先想到分层图最短路 但是因为电梯有负权边所以要跑 \(SPFA\)
结合这题的数据范围 可能会被卡
结果证明好像这题完全不卡
仔细观察 我们会发现只用买卖一次水晶球
还是思考只买卖一次和买卖多次的区别
发现如果只买卖一次 我就可以维护在这个点之前最小的买入价钱和这个点之后最大的卖出价钱 然后相减即可
维护可以用 \(dijktra\) 正反跑两遍
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 0721;
int head1[N], nxt1[N], to1[N], cnt1;
int head2[N], nxt2[N], to2[N], cnt2;
int dis1[N], dis2[N], v[N];
bool vis1[N], vis2[N];
int n, m;
void cmb1(int x, int y) {
to1[++cnt1] = y;
nxt1[cnt1] = head1[x];
head1[x] = cnt1;
}
void cmb2(int x, int y) {
to2[++cnt2] = y;
nxt2[cnt2] = head2[x];
head2[x] = cnt2;
}
struct node1{
int id, dis;
friend bool operator<(node1 a, node1 b) { return a.dis > b.dis; }
};
priority_queue<node1> q1;
inline void dijkstra1(int s) {
memset(dis1, 0x3f, sizeof(dis1));
dis1[s] = v[s];
q1.push((node1){ s, dis1[s] });
while (!q1.empty()) {
int now = q1.top().id;
q1.pop();
if (vis1[now])
continue;
vis1[now] = 1;
for (int i = head1[now]; i; i = nxt1[i]) {
int y = to1[i];
if (dis1[y] > min(dis1[now], v[y])) {
dis1[y] = min(dis1[now], v[y]);
q1.push((node1){ y, dis1[y] });
}
}
}
}
struct node2 {
int id, dis;
friend bool operator<(node2 a, node2 b) { return a.dis < b.dis; }
};
priority_queue<node2> q2;
inline void dijkstra2(int s) {
memset(dis2, -0x3f, sizeof(dis2));
dis2[s] = v[s];
q2.push((node2){ s, dis2[s] });
while (!q2.empty()) {
int now = q2.top().id;
q2.pop();
if (vis2[now])
continue;
vis2[now] = 1;
for (int i = head2[now]; i; i = nxt2[i]) {
int y = to2[i];
if (dis2[y] < max(dis2[now], v[y])) {
dis2[y] = max(dis2[now], v[y]);
q2.push((node2){ y, dis2[y] });
}
}
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &v[i]);
for (int i = 1; i <= m; ++i) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
if (z == 1) {
cmb1(x, y);
cmb2(y, x);
}
else {
cmb1(x, y);
cmb2(y, x);
cmb1(y, x);
cmb2(x, y);
}
}
dijkstra1(1);
dijkstra2(n);
int ans = 0;
for (int i = 1; i <= n; ++i) ans = max(ans, dis2[i] - dis1[i]);
printf("%d", ans);
return 0;
}
D.汽车加油
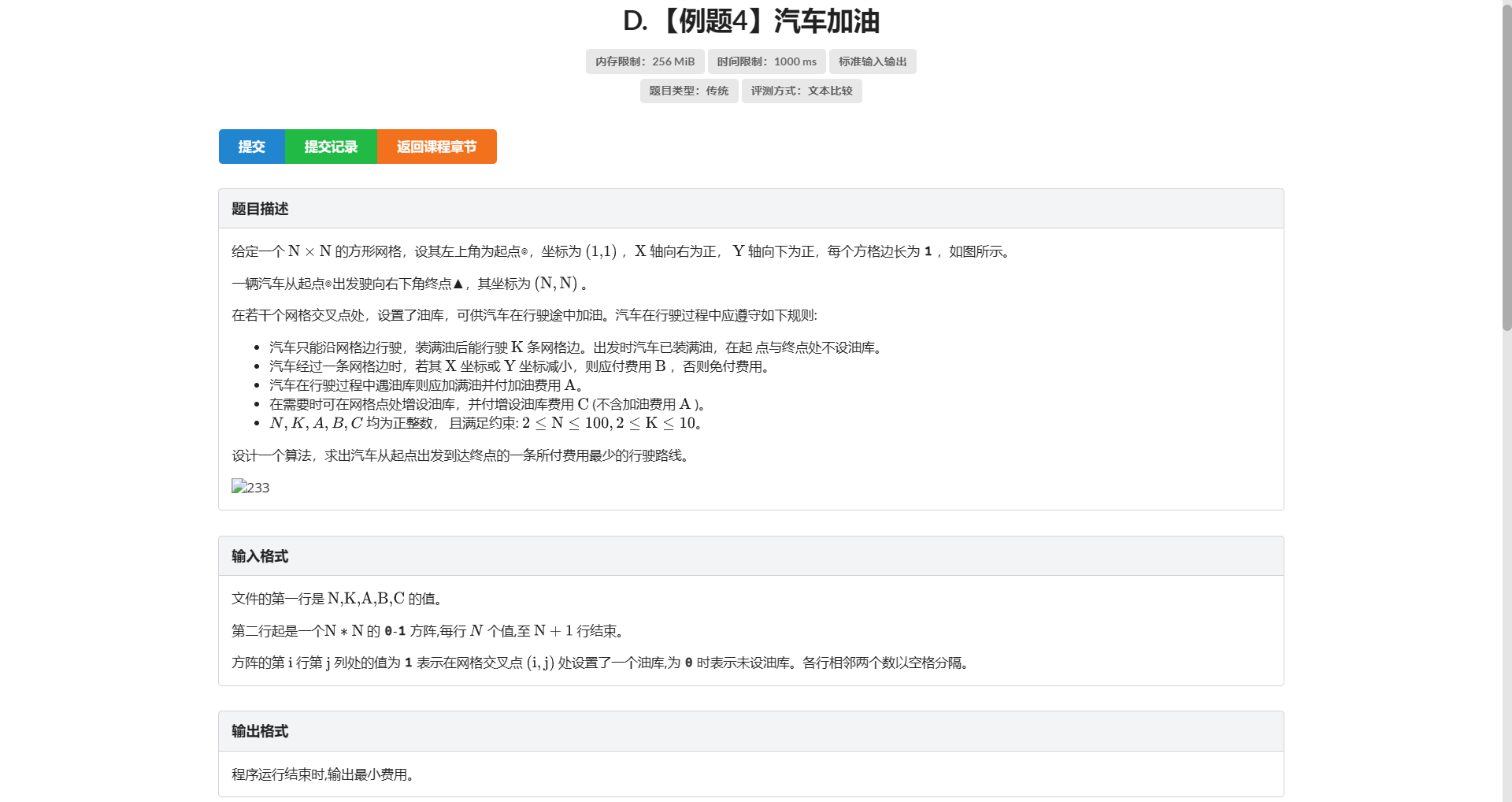
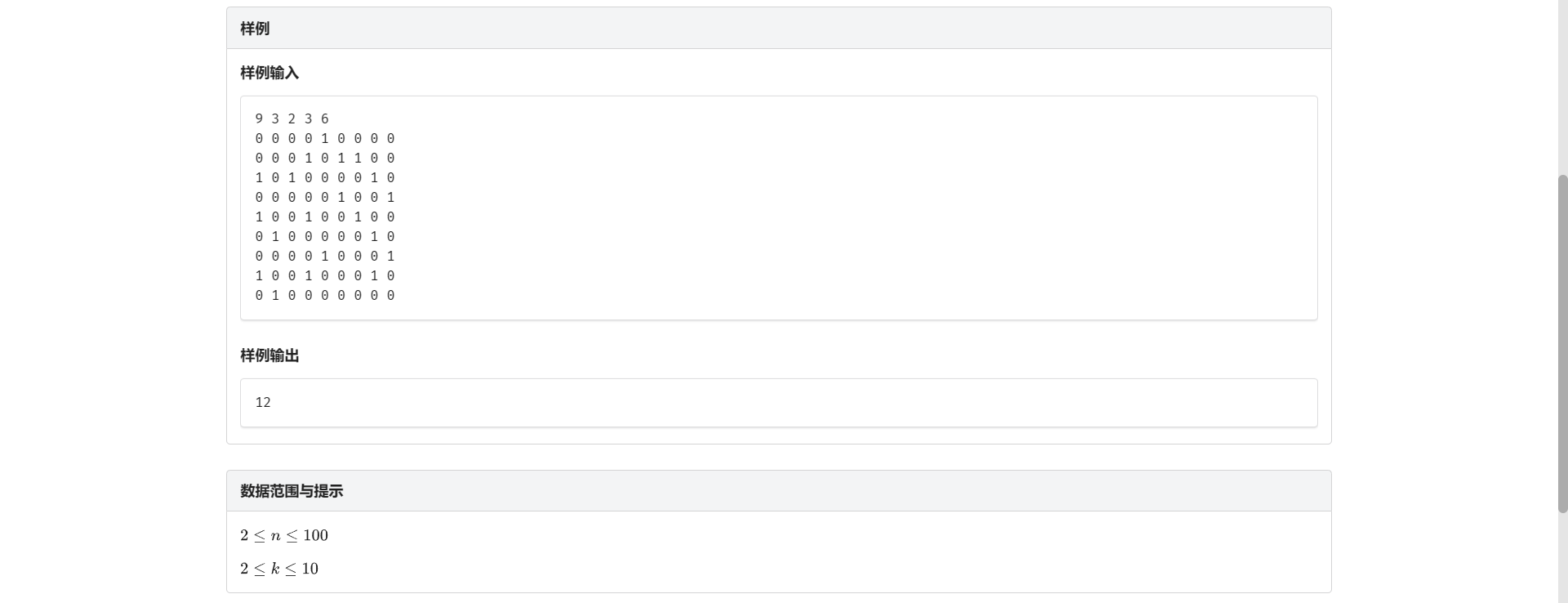
还是能分层图最短路 看起来 \(SPFA\) 还会炸
结果还是完全没卡SPFA!!!
然后发现这是个最小费用最大流 但是我不会网络流
考虑 \(DP\) 设 \(f[i][j][k]\) 表示在 \((i,j)\) 还可以走 \(k\) 条边的最小花费
那么如果这个位置是加油站 就有 \(f[i][j][K] = min(f[i][j][k] + A)\)
如果这个位置没有加油站 可以加油 有 \(f[i][j][K] = min(f[i][j][k] + A + C)\)
如果移动并且 \(x\) 和 \(y\) 坐标没有减少 就有 \(f[i][j][k - 1] = min(f[i'][j'][k])\)
否则 有 \(f[i][j][k - 1] = min(f[i'][j'][k] + B)\)
但是我们显然不清楚枚举顺序 不一定能保证转移的时候前置状态都有
就算清楚了 枚举最小值也有可能T掉
但是突然发现这个玩意长得有点像最短路
所以我们用 \(dijkstra\) 跑
点击查看代码
#include <bits/stdc++.h>
using namespace std;
bool vis[101][101][11];
int dis[101][101][11], mp[101][101];
int dx[4] = { 0, 1, 0, -1 };
int dy[4] = { 1, 0, -1, 0 };
int n, k, a, b, c;
inline bool check(int x, int y) {
return x >= 1 && x <= n && y >= 1 && y <= n;
}
struct node {
int x, y, fuel, cost;
friend bool operator<(node a, node b) { return a.cost > b.cost; };
};
priority_queue<node> q;
inline void dijkstra(void) {
memset(dis, 0x3f, sizeof(dis));
dis[1][1][k] = 0;
q.push((node){ 1, 1, k, 0 });
while (!q.empty()) {
node now = q.top();
q.pop();
if (vis[now.x][now.y][now.fuel])
continue;
vis[now.x][now.y][now.fuel] = 1;
if (mp[now.x][now.y] && now.fuel != k) {
if (dis[now.x][now.y][k] > dis[now.x][now.y][now.fuel] + a) {
dis[now.x][now.y][k] = dis[now.x][now.y][now.fuel] + a;
q.push((node){ now.x, now.y, k, dis[now.x][now.y][k] });
}
continue;
}
else {
if (dis[now.x][now.y][k] > dis[now.x][now.y][now.fuel] + a + c) {
dis[now.x][now.y][k] = dis[now.x][now.y][now.fuel] + a + c;
q.push((node){ now.x, now.y, k, dis[now.x][now.y][k] });
}
}
if (now.fuel > 0) {
for (int i = 0; i < 4; ++i) {
int tox = now.x + dx[i], toy = now.y + dy[i];
if (check(tox, toy)) {
int w = 0;
if (tox < now.x || toy < now.y)
w = b;
if (dis[tox][toy][now.fuel - 1] > dis[now.x][now.y][now.fuel] + w) {
// if (tox == n && toy == n)
// cout<<now.x<<" "<<now.y<<" "<<now.fuel<<endl;
dis[tox][toy][now.fuel - 1] = dis[now.x][now.y][now.fuel] + w;
q.push((node){ tox, toy, now.fuel - 1, dis[tox][toy][now.fuel - 1] });
}
}
}
}
}
}
int main() {
scanf("%d%d%d%d%d", &n, &k, &a, &b, &c);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) scanf("%d", &mp[i][j]);
}
dijkstra();
int ans = 0x7fffffff;
for (int i = 0; i <= k; ++i)
ans = min(ans, dis[n][n][i]);
printf("%d",ans);
return 0;
}
E.最小花费
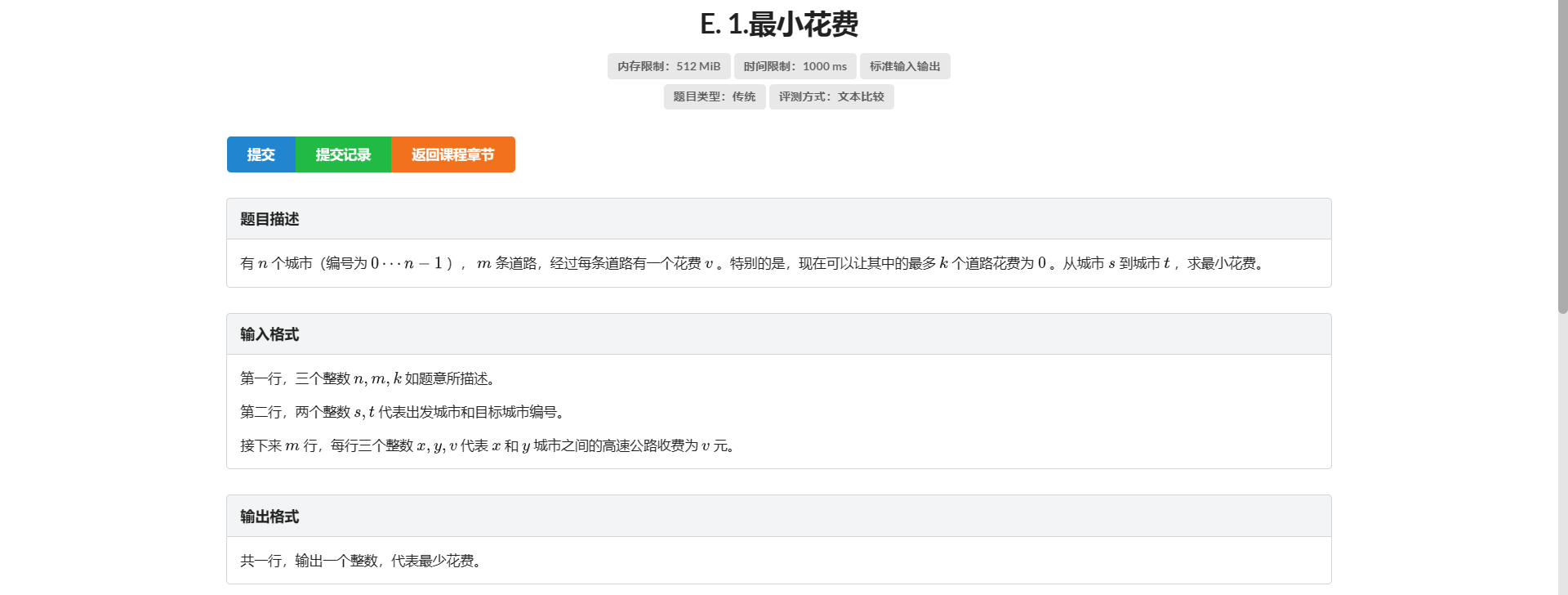
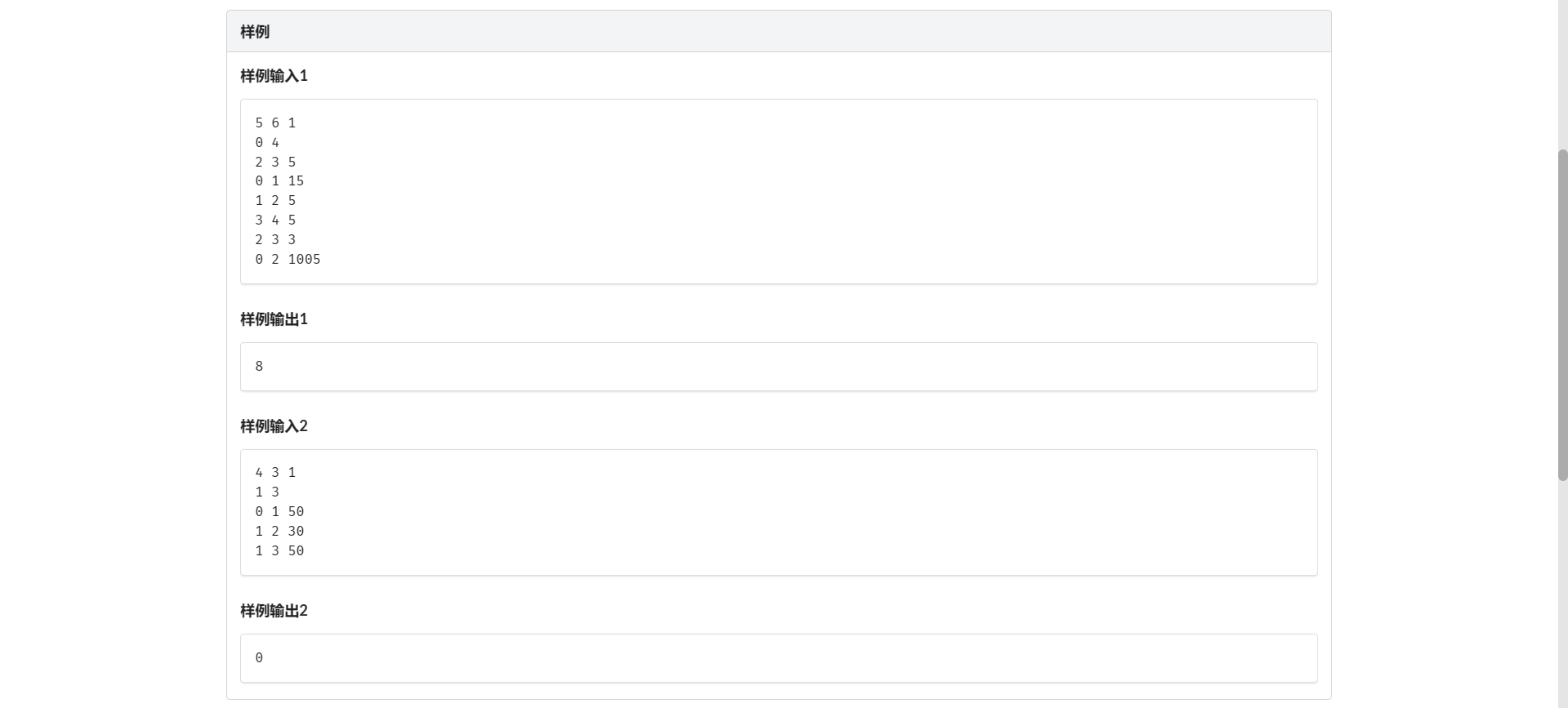

刚开始受某种宇宙射线影响 想到设 \(dis_{x, y}\) 表示 \(s \rightarrow x\) 走 \(y\) 次免费路的最小距离
然后发现这玩意不就是分层图最短路裸题吗
太久没敲 dijkstra 发现嗷嗷挂 太下饭了
记得建电梯 或者把终点的每一层都扫一遍也行
另外吐槽一句分层图空间狗都不算!
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 2e5 + 0721;
const int M = 5e6 + 0721;
int head[N], nxt[M], to[M], len[M], cnt;
int dis[N];
bool vis[N];
int n, m, k;
int s, t;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void add_edge(int x, int y, int z) {
// cout << x << " " << y << " " << z << "\n";
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
len[cnt] = z;
}
struct node {
int id, dis;
friend bool operator<(node x, node y) {
return x.dis > y.dis;
}
};
priority_queue<node> q;
void dijkstra() {
memset(dis, 0x3f, sizeof dis);
dis[s] = 0;
q.push((node){s, 0});
while (!q.empty()) {
int now = q.top().id;
q.pop();
if (vis[now]) continue;
vis[now] = 1;
// cout << now << "\n";
for (int i = head[now]; i; i = nxt[i]) {
int y = to[i];
// cout << y << " " << dis[now] + len[i] << "\n";
if (dis[y] > dis[now] + len[i]) {
// cout << y << " " << dis[now] + len[i] << "\n";
dis[y] = dis[now] + len[i];
q.push((node){y, dis[y]});
}
}
}
}
void main() {
n = read(), m = read(), k = read();
s = read(), t = read();
++s, ++t;
for (int i = 1; i <= m; ++i) {
int x, y, z;
x = read(), y = read(), z = read();
++x, ++y;
// cout << x << " " << y << " " << z << "\n";
for (int base = 0; base <= k; ++base) {
add_edge(x + base * n, y + base * n, z);
add_edge(y + base * n, x + base * n, z);
}
for (int base = 0; base < k; ++base) {
add_edge(x + base * n, y + n * (base + 1), 0);
add_edge(y + base * n, x + n * (base + 1), 0);
}
}
for (int i = 1; i <= n; ++i) {
for (int base = 0; base < k; ++base) add_edge(i + base * n, i + n * (base + 1), 0);
}
dijkstra();
printf("%d\n", dis[t + n * k]);
}
}
int main() {
steven24::main();
return 0;
}
/*
5 6 1
0 4
2 3 5
0 1 15
1 2 5
3 4 5
2 3 3
0 2 1005
*/
F.修建道路
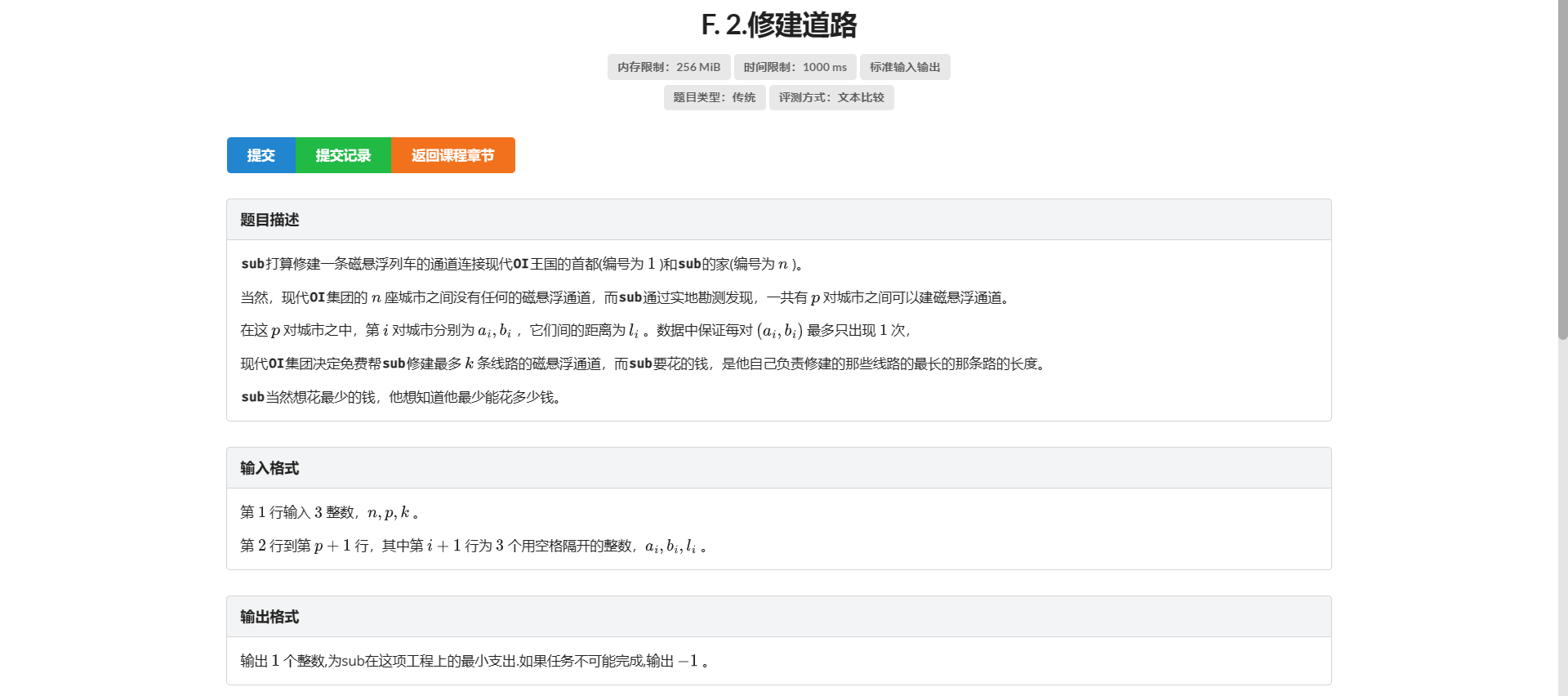
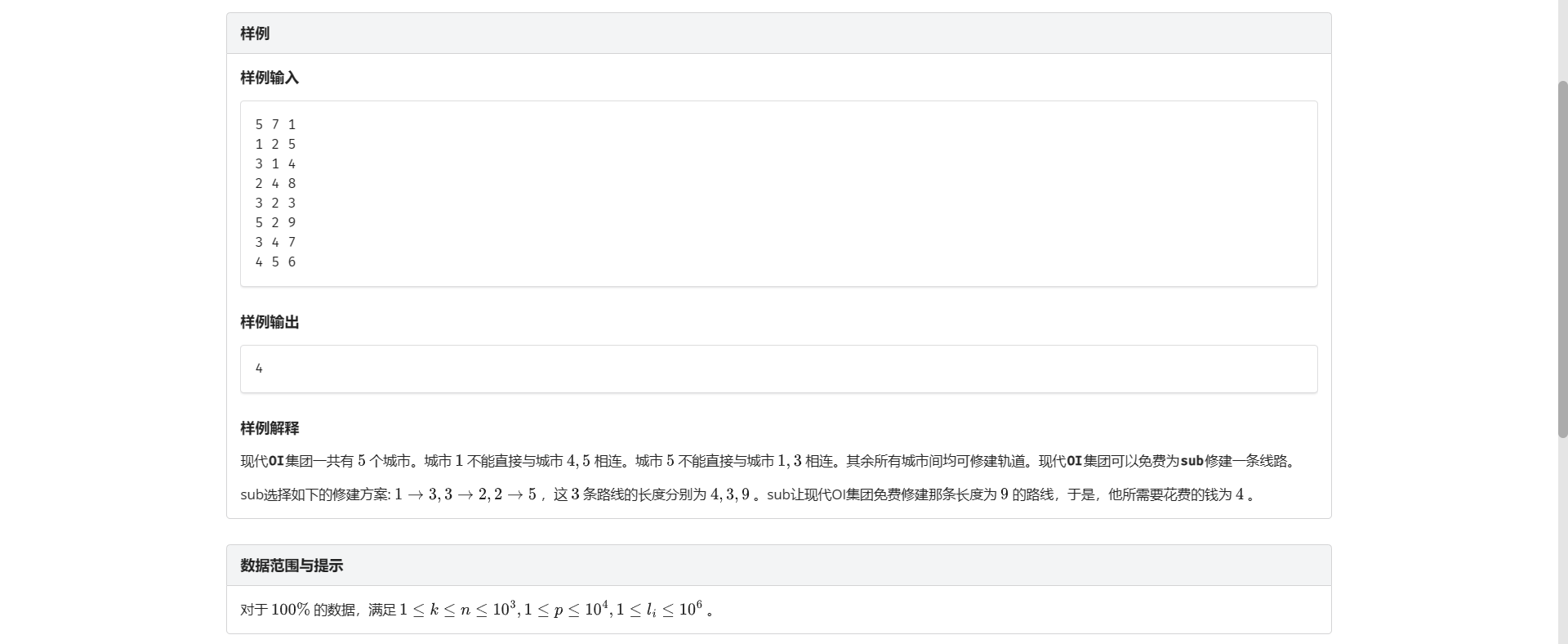
看傻了
这不就上一题改两行吗
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 2e5 + 0721;
const int M = 5e6 + 0721;
int head[N], nxt[M], to[M], len[M], cnt;
int dis[N];
bool vis[N];
int n, m, k;
int s, t;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void add_edge(int x, int y, int z) {
// cout << x << " " << y << " " << z << "\n";
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
len[cnt] = z;
}
struct node {
int id, dis;
friend bool operator<(node x, node y) {
return x.dis > y.dis;
}
};
priority_queue<node> q;
void dijkstra() {
memset(dis, 0x3f, sizeof dis);
dis[s] = 0;
q.push((node){s, 0});
while (!q.empty()) {
int now = q.top().id;
q.pop();
if (vis[now]) continue;
vis[now] = 1;
for (int i = head[now]; i; i = nxt[i]) {
int y = to[i];
if (dis[y] > max(dis[now], len[i])) {
dis[y] = max(dis[now], len[i]);
q.push((node){y, dis[y]});
}
}
}
}
void main() {
n = read(), m = read(), k = read();
s = 1, t = n;
for (int i = 1; i <= m; ++i) {
int x, y, z;
x = read(), y = read(), z = read();
// cout << x << " " << y << " " << z << "\n";
for (int base = 0; base <= k; ++base) {
add_edge(x + base * n, y + base * n, z);
add_edge(y + base * n, x + base * n, z);
}
for (int base = 0; base < k; ++base) {
add_edge(x + base * n, y + n * (base + 1), 0);
add_edge(y + base * n, x + n * (base + 1), 0);
}
}
for (int i = 1; i <= n; ++i) {
for (int base = 0; base < k; ++base) add_edge(i + base * n, i + n * (base + 1), 0);
}
dijkstra();
if (dis[t + n * k] != 0x3f3f3f3f) printf("%d\n", dis[t + n * k]);
else printf("-1\n");
}
}
int main() {
steven24::main();
return 0;
}
/*
5 7 1
1 2 5
3 1 4
2 4 8
3 2 3
5 2 9
3 4 7
4 5 6
*/
G.糖果分配
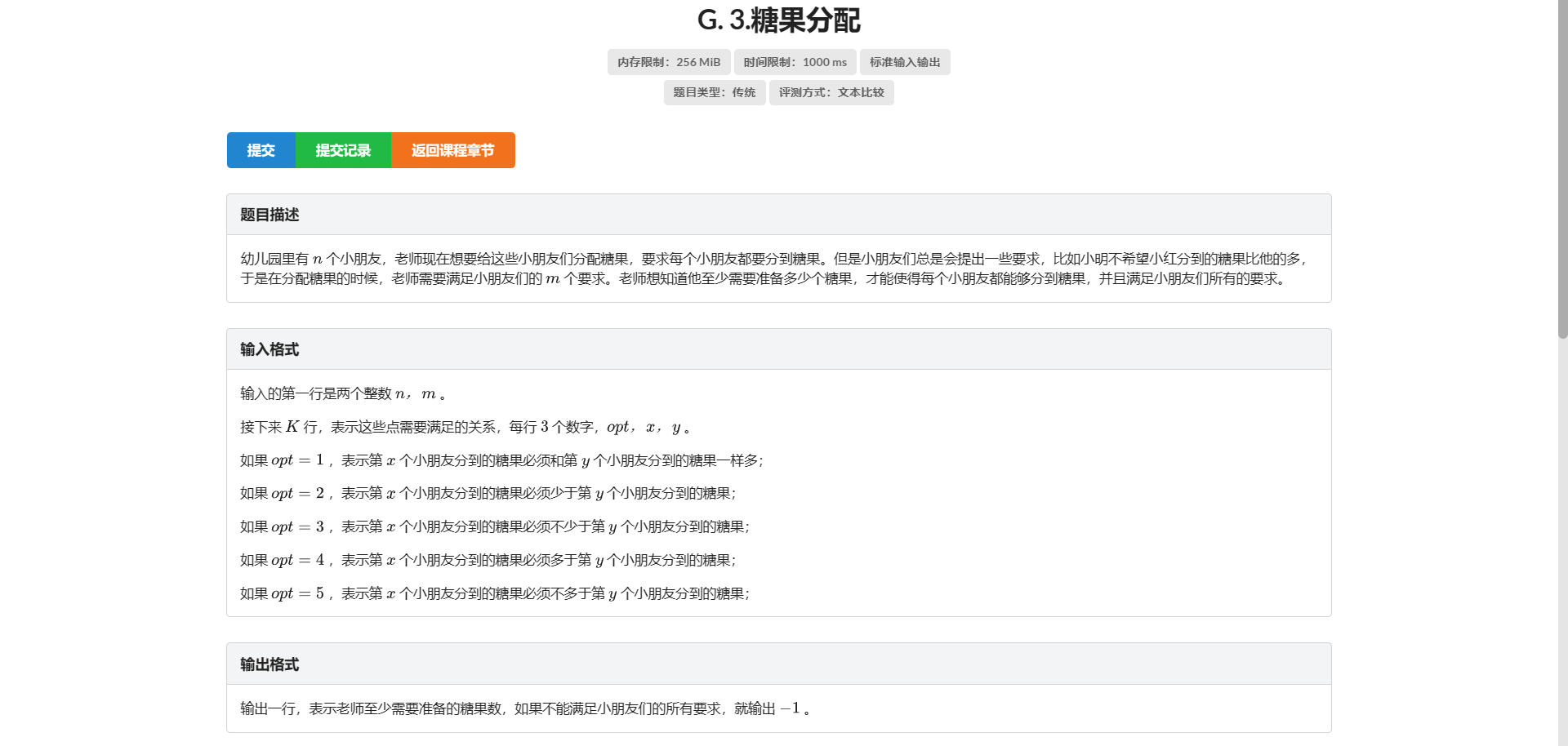
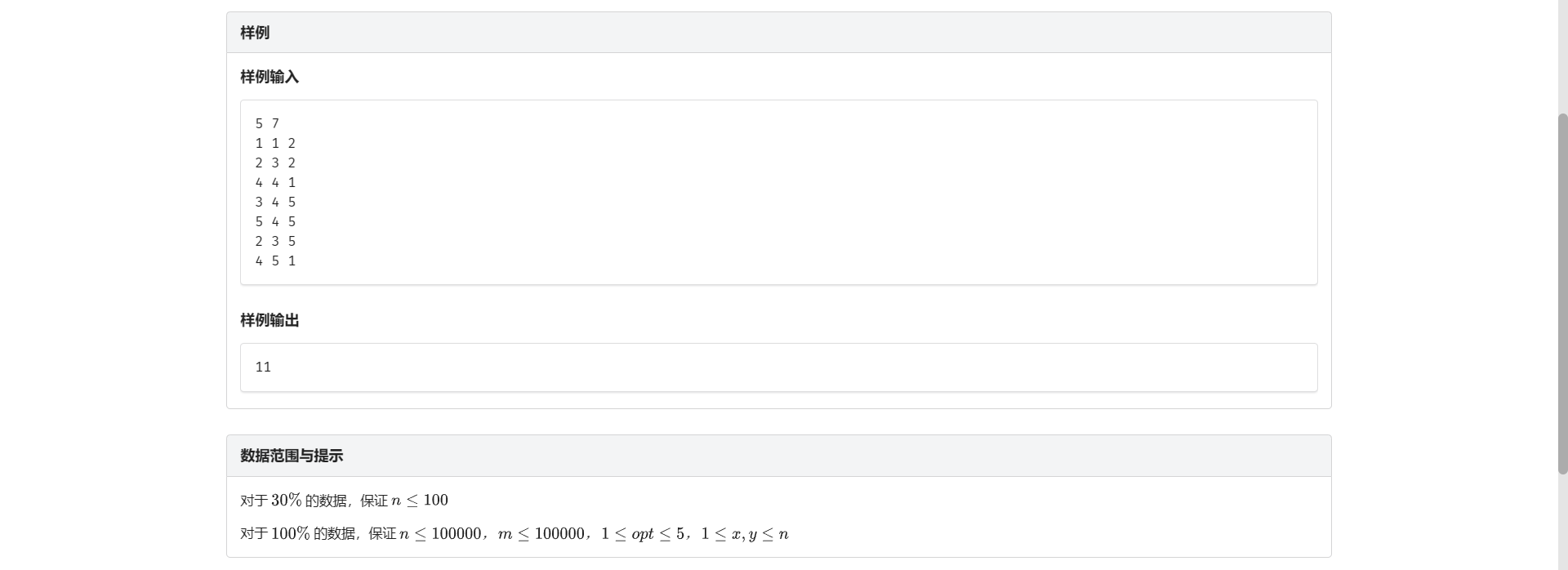
怎么又是裸题啊
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 3e5 + 0721;
int head[N], to[N], nxt[N], len[N], cnt;
int sccnum[N], sccsz[N], sccsiz[N], dfn[N], low[N], q[N], dfs_clock, scccnt, top;
int head1[N], to1[N], nxt1[N], len1[N], cnt1;
int dis[N];
int n, m;
inline void cmb(int x, int y, int z) {
to[++cnt] = y;
len[cnt] = z;
nxt[cnt] = head[x];
head[x] = cnt;
}
inline void tarjan(int x) {
dfn[x] = low[x] = ++dfs_clock;
q[++top] = x;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (!sccnum[y]) {
low[x] = min(low[x], dfn[y]);
}
}
if (dfn[x] == low[x]) {
++scccnt;
while (1) {
int now = q[top];
--top;
sccnum[now] = scccnt;
++sccsiz[scccnt];
if (now == x)
break;
}
}
}
inline void cmb1(int x, int y, int z) {
to1[++cnt1] = y;
len1[cnt1] = z;
nxt1[cnt1] = head1[x];
head1[x] = cnt1;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int x, y, num;
scanf("%d%d%d", &num, &x, &y);
if (num == 1)
cmb(x, y, 0), cmb(y, x, 0);
else if (num == 2)
cmb(x, y, 1);
else if (num == 3)
cmb(y, x, 0);
else if (num == 4)
cmb(y, x, 1);
else
cmb(x, y, 0);
}
for (int i = 1; i <= n; ++i) cmb(0, i, 0);
tarjan(0);
for (int i = 0; i <= n; ++i) {
for (int j = head[i]; j; j = nxt[j]) {
int y = to[j];
if (sccnum[i] != sccnum[y])
cmb1(sccnum[i], sccnum[y], len[j]);
else
sccsz[sccnum[i]] += len[j];
}
}
for (int i = 1; i <= scccnt; ++i) {
if (sccsz[i] != 0) {
printf("-1");
return 0;
}
}
// cout<<"!";
ll ans = 0;
for (int i = 1; i <= scccnt; ++i) dis[i] = 1;
for (int i = scccnt; i >= 1; --i) {
for (int j = head1[i]; j; j = nxt1[j]) {
int y = to1[j];
// cout<<y<<" "<<dis[y]<<" "<<len1[j]<<endl;
dis[y] = max(dis[y], dis[i] + len1[j]);
}
}
for (int i = 1; i < scccnt; ++i) ans += (ll)dis[i] * sccsiz[i];
printf("%lld", ans);
return 0;
}
H.比较大小
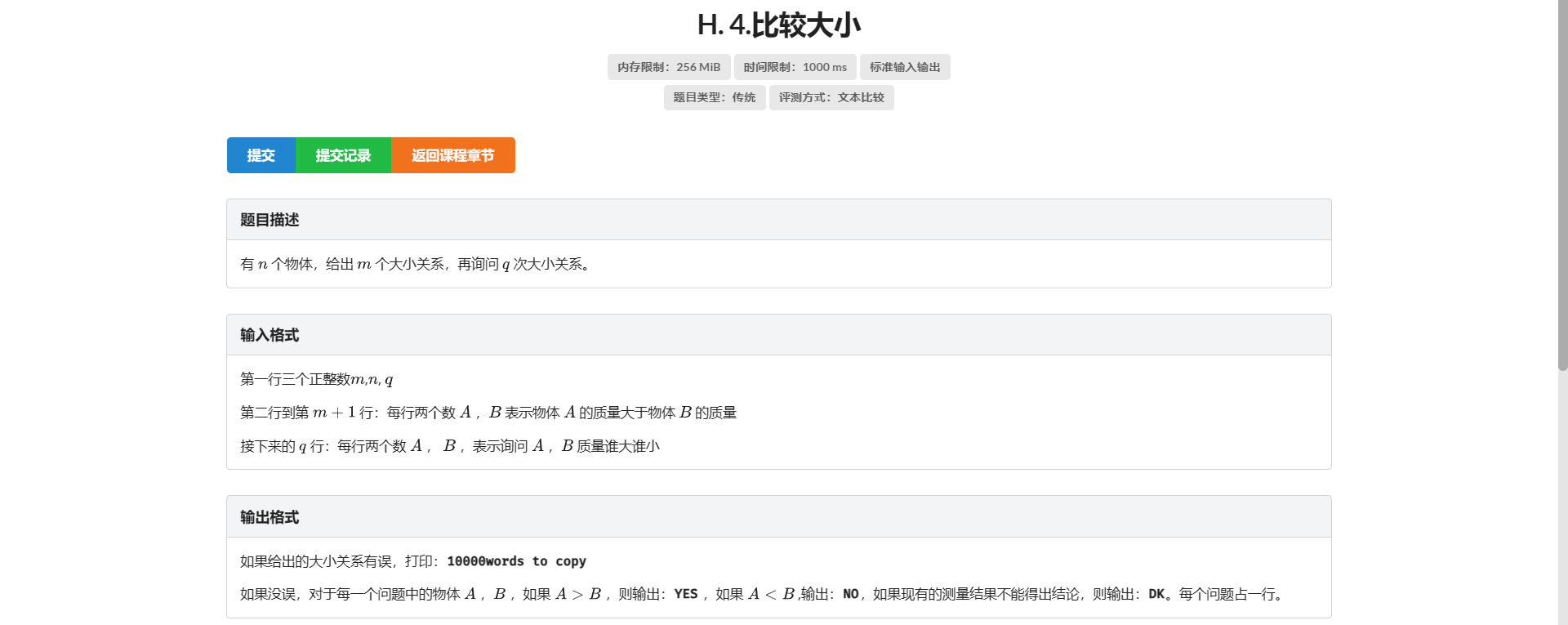
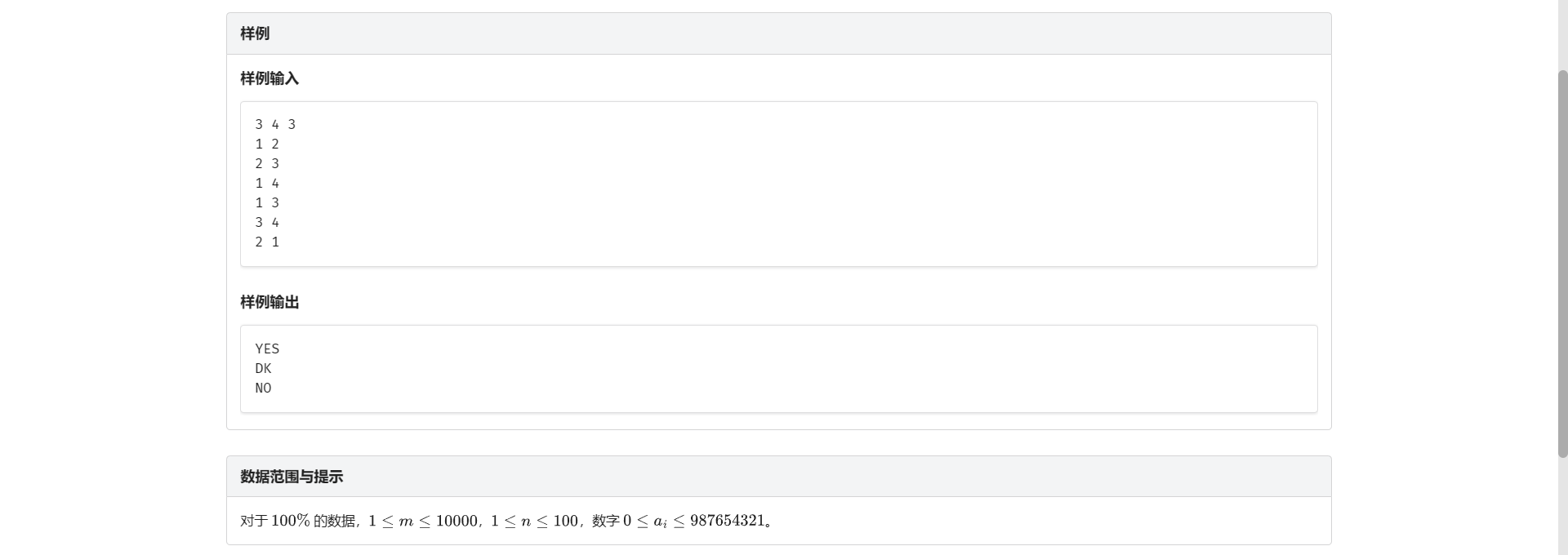
一眼不就是差分约束裸题吗
然后码码码
发现没有 DK
然后加了个对每个点暴力 dfs
然后就过了样例
结果 bellman-ford 写炸了硬是交到第三发才过
这下下饭了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int M = 10521;
const int N = 121;
int head[N], nxt[M], to[M], len[M], cnt;
int dis[N];
bool vis[N][N];
int n, m, q;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void add_edge(int x, int y, int z) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
len[cnt] = z;
}
bool bellman_ford() {
memset(dis, 0x3f, sizeof dis);
dis[0] = 0;
bool flag = 1;
for (int k = 1; k <= n; ++k) {
flag = 0;
for (int i = 0; i <= n; ++i) {
for (int j = head[i]; j; j = nxt[j]) {
int y = to[j];
if (dis[y] > dis[i] + len[j]) {
dis[y] = dis[i] + len[j];
flag = 1;
}
}
}
if (!flag) break;
}
return flag;
}
void dfs(int x, int s) {
vis[s][x] = 1;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (!vis[s][y]) dfs(y, s);
}
}
void main() {
m = read(), n = read(), q = read();
for (int i = 1; i <= n; ++i) add_edge(0, i, 0);
for (int i = 1; i <= m; ++i) {
int a, b;
a = read(), b = read();
add_edge(a, b, -1);
}
if (bellman_ford()) {
printf("10000words to copy\n");
return;
}
for (int i = 1; i <= n; ++i) dfs(i, i);
// for (int i = 1; i <= n; ++i) cout << "val" << i << " = " << dis[i] << "\n";
while (q--) {
int a, b;
a = read(), b = read();
if (!vis[a][b] && !vis[b][a]) printf("DK\n");
else if (dis[a] > dis[b]) printf("YES\n");
else printf("NO\n");
}
}
}
int main() {
steven24::main();
return 0;
}
/*
3 4 3
1 2
2 3
1 4
1 3
3 4
2 1
*/
I.删边问题
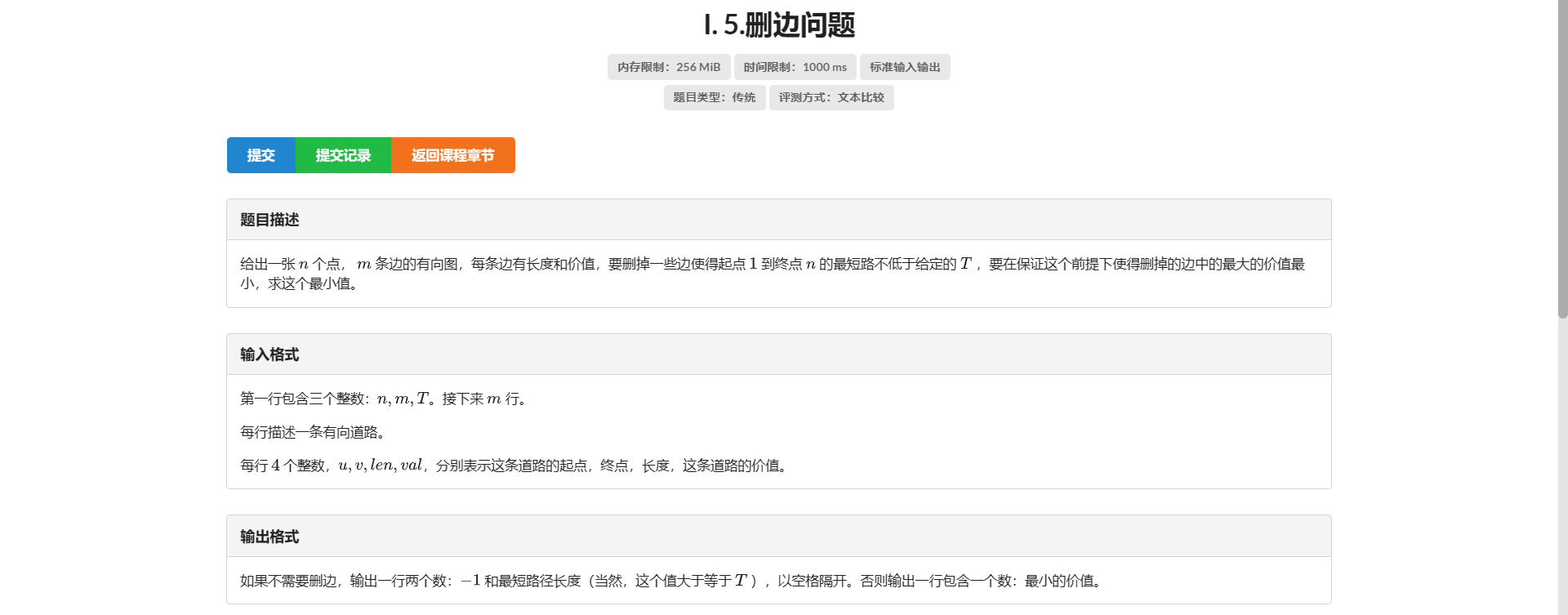
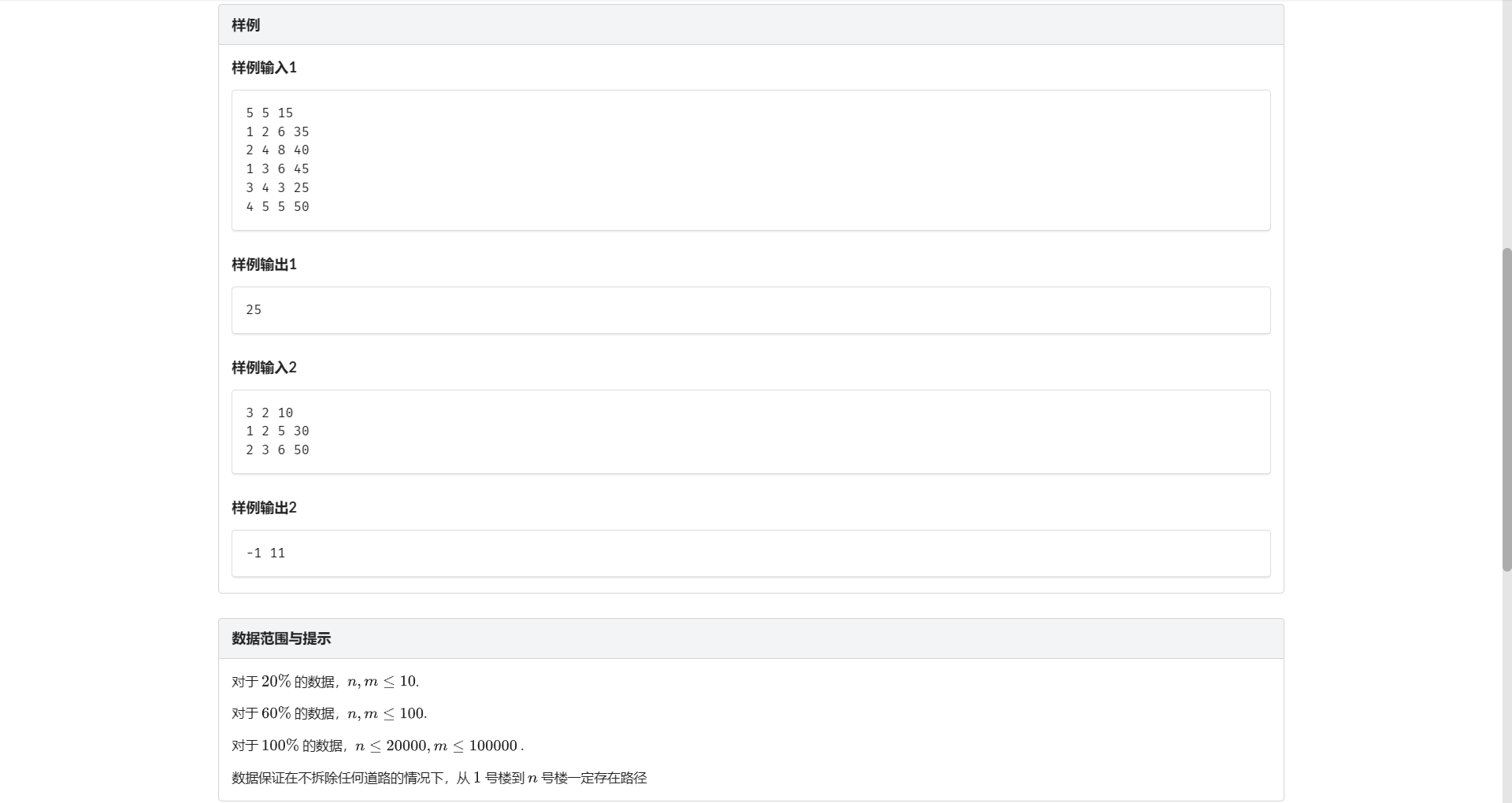
一眼二分 水题秒了
然后被水题秒了
因为答案一定是存在的边权 所以先对边权进行离散化
二分边界改变写反了 怎么这么菜啊。
点击查看代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
namespace steven24 {
const int N = 2e4 + 0721;
const int M = 1e5 + 0721;
int head[N], nxt[M], to[M], len[M], val[M], cnt;
int dis[N];
int a[M];
bool vis[N];
int n, m, T;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void add_edge(int x, int y, int z, int zz) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
len[cnt] = z;
val[cnt] = zz;
}
struct node {
int id, dis;
friend bool operator<(node x, node y) {
return x.dis > y.dis;
}
};
priority_queue<node> q;
bool dijkstra(int x) { //把<=x的都删掉
memset(dis, 0x3f, sizeof dis);
memset(vis, 0, sizeof vis);
dis[1] = 0;
q.push((node){1, 0});
while (!q.empty()) {
int now = q.top().id;
q.pop();
if (vis[now]) continue;
vis[now] = 1;
// cout << now << "\n";
for (int i = head[now]; i; i = nxt[i]) {
int y = to[i];
// cout << y << " " << len[i] << " " << dis[x] << "\n";
if (val[i] <= x) continue;
if (dis[y] > dis[now] + len[i]) {
dis[y] = dis[now] + len[i];
q.push((node){y, dis[y]});
}
}
}
// cout << x << " " << dis[n] << "\n";
return dis[n] >= T;
}
void main() {
n = read(), m = read(), T = read();
int tot = 0;
a[++tot] = 0;
for (int i = 1; i <= m; ++i) {
int x, y, z, zz;
x = read(), y = read(), z = read(), zz = read();
add_edge(x, y, z, zz);
a[++tot] = zz;
}
sort(a + 1, a + 1 + tot);
int l = 1, r = tot;
int mid, ans;
while (l <= r) {
mid = (l + r) >> 1;
if (dijkstra(a[mid])) {
ans = mid;
r = mid - 1;
} else
l = mid + 1;
}
if (ans == 1) {
dijkstra(0);
printf("-1 %lld\n", dis[n]);
} else
printf("%lld\n", a[ans]);
}
}
signed main() {
steven24::main();
return 0;
}
/*
5 5 15
1 2 6 35
2 4 8 40
1 3 6 45
3 4 3 25
4 5 5 50
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号