YBTOJ 3.2最小生成树
前注:本文涉及的所有求最小生成树的算法均为 \(kruskal\)
A.繁忙都市
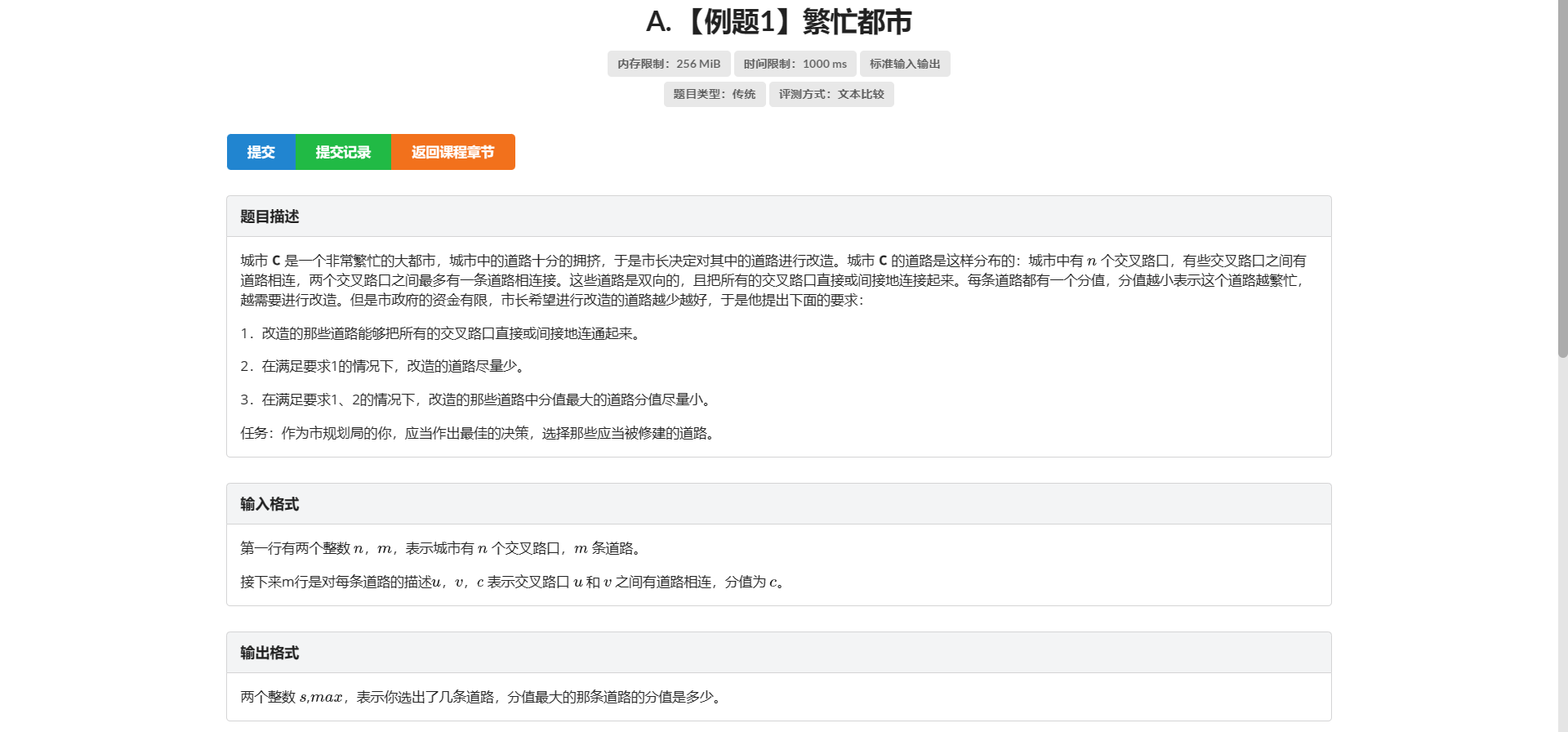
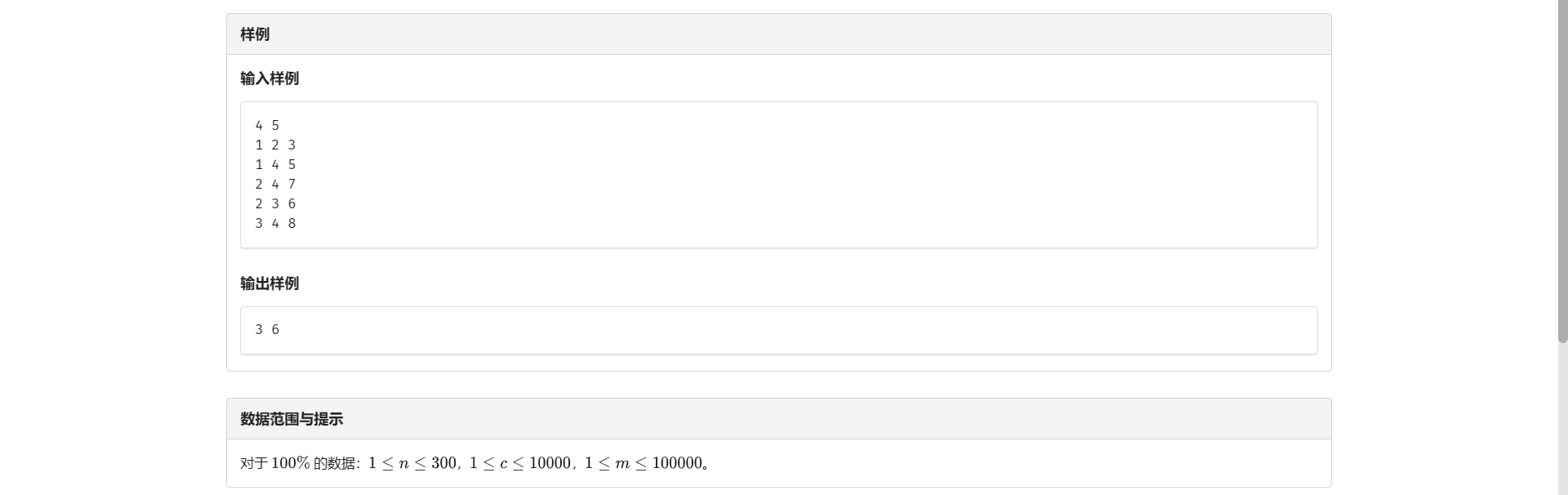
要求联通并且边最少
\(n\) 个节点联通最少要 \(n - 1\) 条边
那不就是棵树嘛
然后跑最小生成树就行了
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
struct node {
int u, v, w;
} st[N];
int n, m;
int fa[N];
int cnt, ans;
bool cmp(node x, node y) { return x.w < y.w; }
int find(int x) {
if (fa[x] == x)
return x;
else
return fa[x] = find(fa[x]);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
scanf("%d%d%d", &st[i].u, &st[i].v, &st[i].w);
}
sort(st + 1, st + 1 + m, cmp);
for (int i = 1; i <= n; ++i) fa[i] = i;
for (int i = 1; i <= m; ++i) {
int fr = st[i].u, to = st[i].v, l = st[i].w;
if (find(fr) != find(to)) {
int ffr = fa[fr], fto = fa[to];
fa[ffr] = fto;
cnt++;
ans = max(ans, l);
}
if (cnt == n - 1)
break;
}
printf("%d %d", n - 1, ans);
return 0;
}
B.新的开始
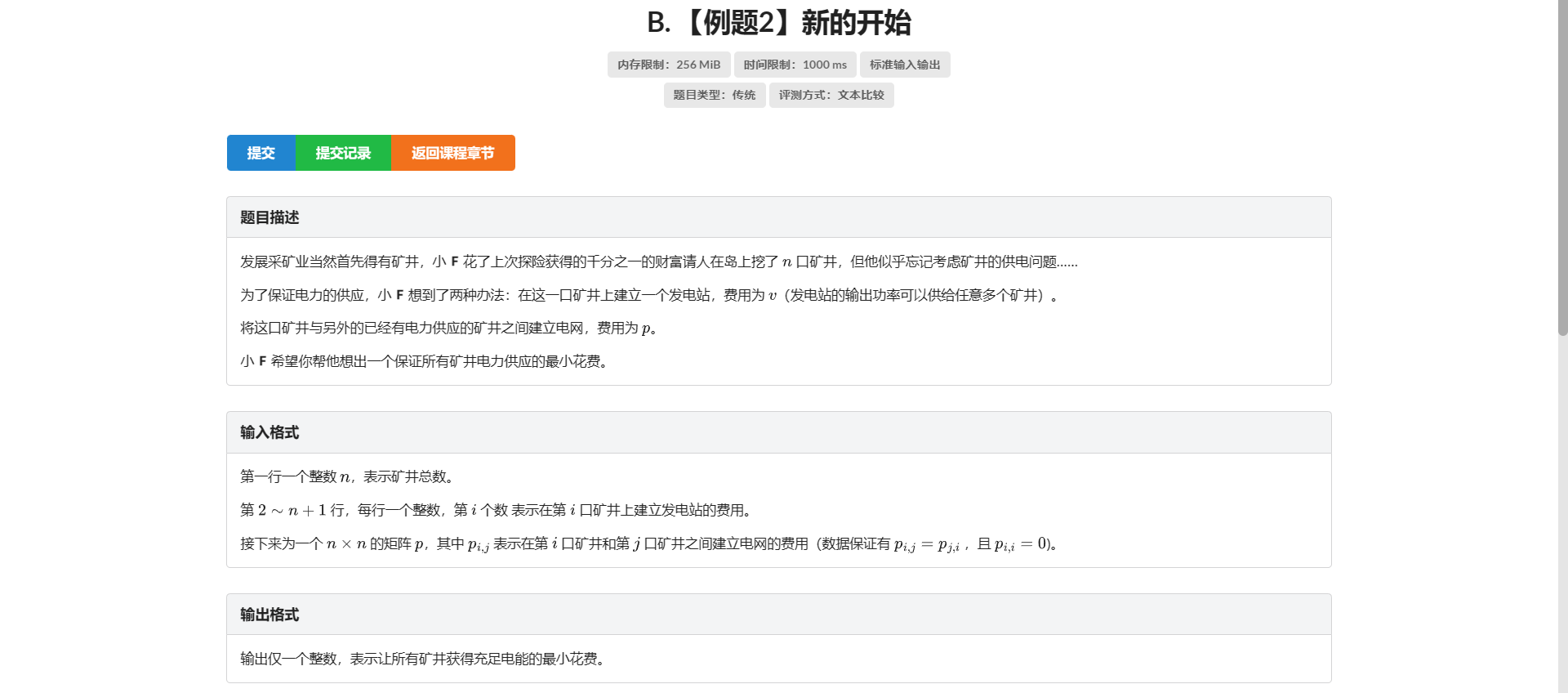
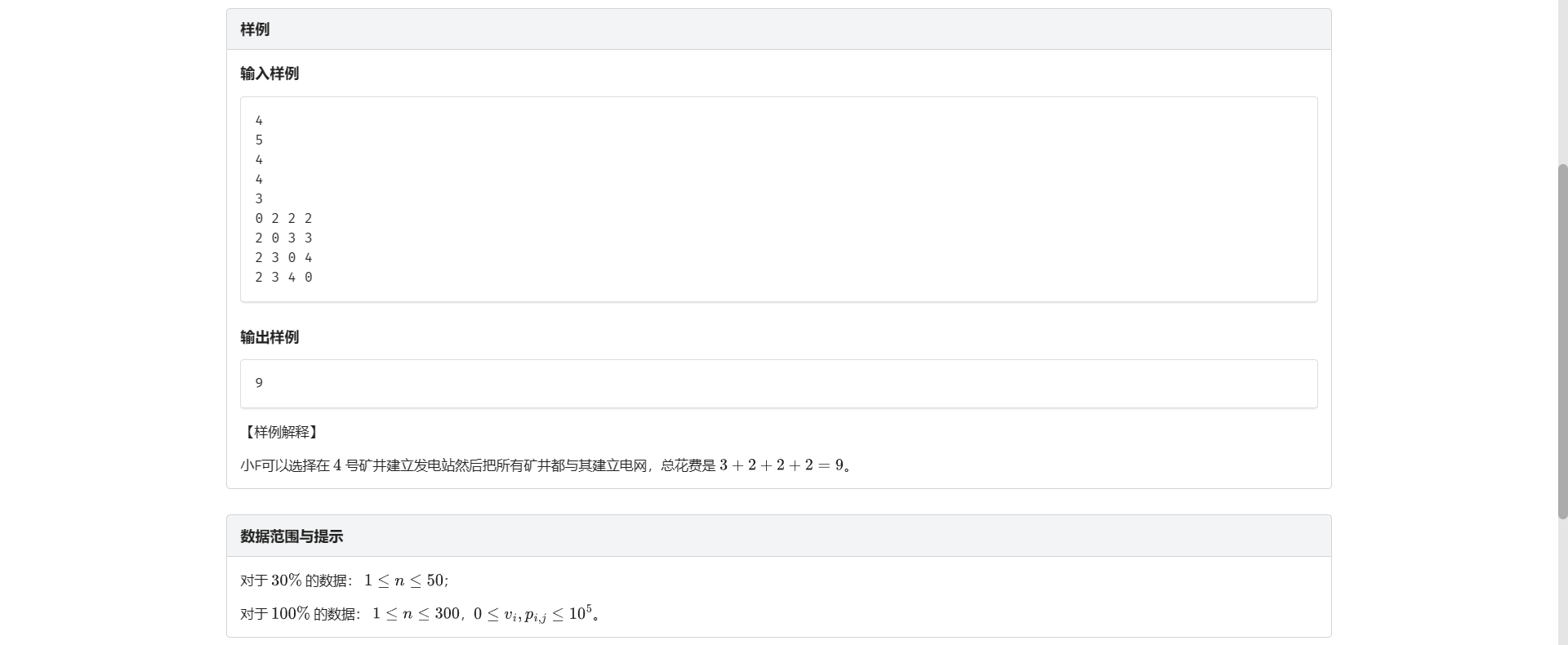
让所有点联通 想到最小生成树
但是造电站怎么表示啊 我总不可能枚举每个点造/不造电站的情况吧
那么假如 我是说假如 我把造电站转化成和什么玩意连条边
那么跑个最小生成树就结束了对吧
进一步我们想到用一个超级原点 把造电站转化为和这个超级原点连边
然后带着超级原点跑最小生成树
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 0721;
const int maxn = 5e5 + 0721;
bool vis[N][N];
int fa[N];
int n, cnt;
ll ans;
struct node {
int x, y, val;
friend bool operator<(node a, node b) { return a.val < b.val; }
} edge[maxn];
int find(int x) {
if (x == fa[x])
return fa[x];
else
return fa[x] = find(fa[x]);
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int x;
scanf("%d", &x);
edge[++cnt].x = 0, edge[cnt].y = i, edge[cnt].val = x;
vis[0][i] = 1;
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
int x;
scanf("%d", &x);
if (vis[i][j])
continue;
if (i == j)
continue;
edge[++cnt].x = i, edge[cnt].y = j, edge[cnt].val = x;
vis[i][j] = vis[j][i] = 1;
}
}
for (int i = 1; i <= n; ++i) fa[i] = i;
sort(edge + 1, edge + 1 + cnt);
for (int i = 1; i <= cnt; ++i) {
int fx = find(edge[i].x), fy = find(edge[i].y);
if (fx != fy) {
ans += edge[i].val;
fa[fx] = fy;
}
}
printf("%lld", ans);
return 0;
}
C.公路建设
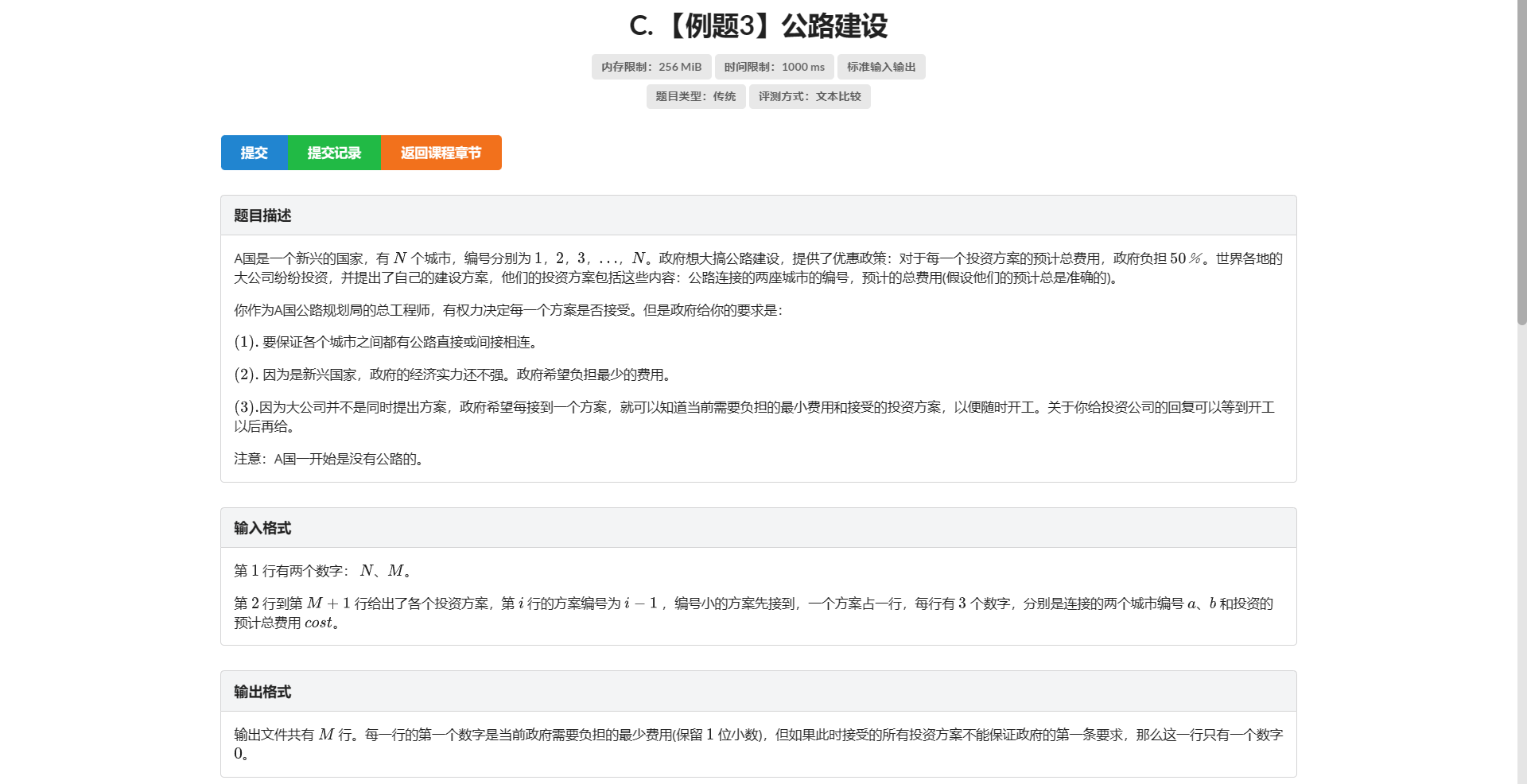
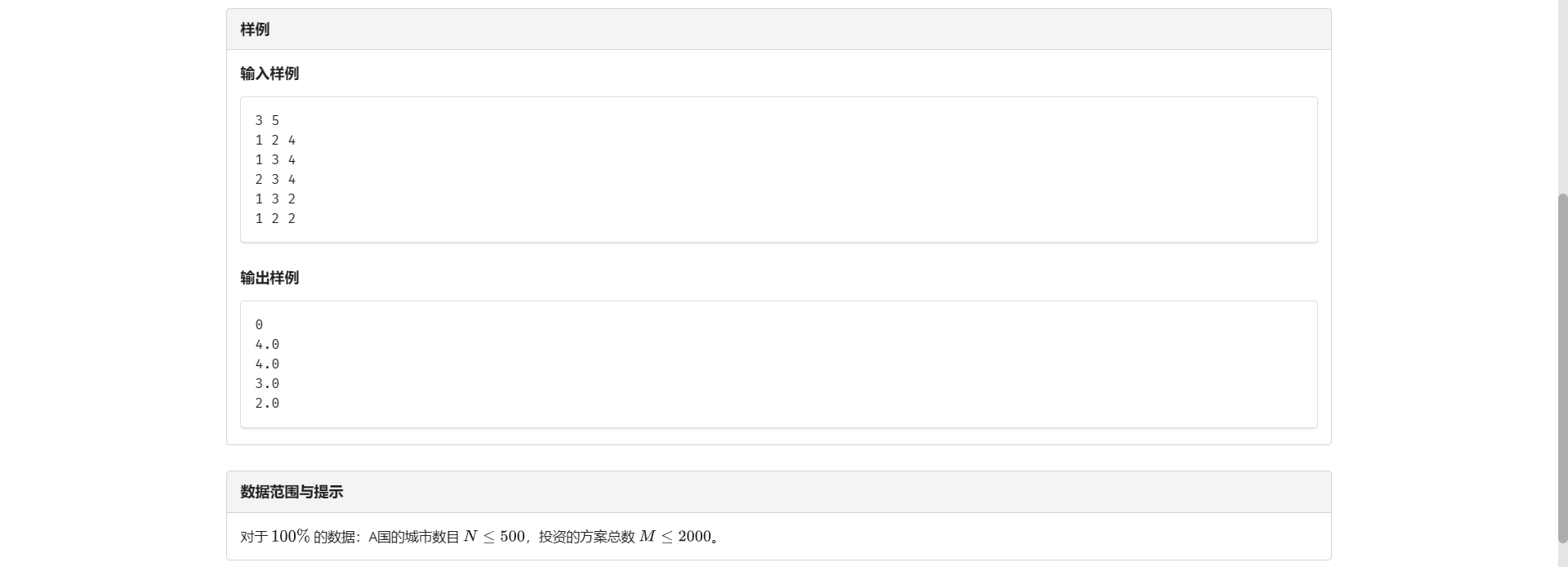
首先还是 根据题干几个限制条件可以看出来是求最小生成树
有个非常暴力的思想就是我每次重新加边就跑一次最小生成树
但是 \(O(m^2logm)\) 不太容易能过去 考虑优化
首先 \(m\) 是肯定不能省的 至少你输出都得占一个 \(m\)
那么瓶颈就产生在排序的复杂度
思考一下本题的排序有什么特殊点
发现每次排序实质上只是加了一条新边进去
那完全可以暴力冒泡 复杂度是 \(O(m)\) 的
总复杂度就是 \(O(m^2)\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 0x0d00;
struct node {
int u, v, w;
}edge[N];
int fa[N];
int n, m, cnt;
node a[N];
int find(int x) {
if (x == fa[x])
return fa[x];
else
return fa[x] = find(fa[x]);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].w);
a[++cnt] = edge[i];
for (int j = cnt; j >= 1; --j) {
if (a[j].w < a[j - 1].w)
swap(a[j], a[j - 1]);
}
for (int j = 1; j <= n; ++j)
fa[j] = j;
int ans = 0, k = 0;
for (int j = 1; j <= cnt; ++j) {
int fu = find(a[j].u), fv = find(a[j].v);
if (fu != fv) {
ans += a[j].w;
fa[fu] = fv;
}
else
k = j;
}
if (k) {
--cnt;
for (int j = k; j <= cnt; ++j)
swap(a[j], a[j + 1]);
}
if (cnt != n - 1)
printf("0\n");
else
printf("%0.1lf\n", ans / 2.0);
}
return 0;
}
D.构造完全图
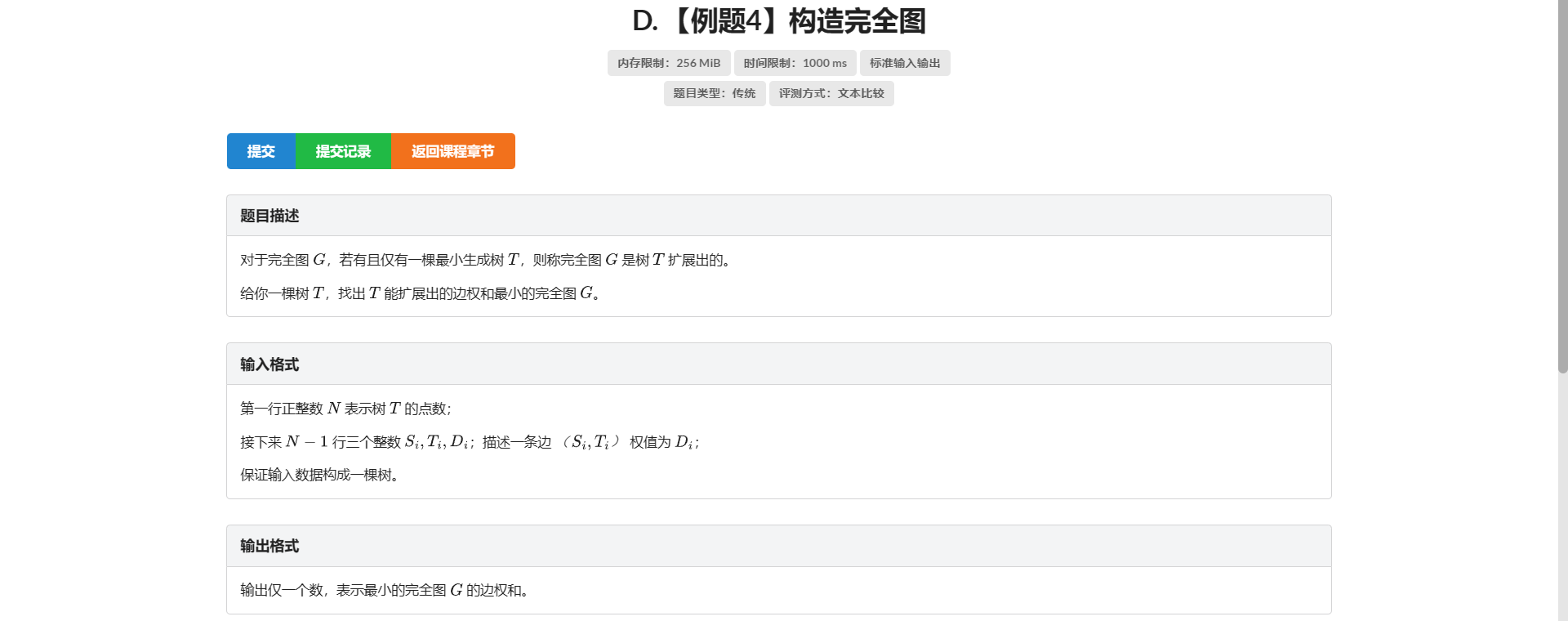
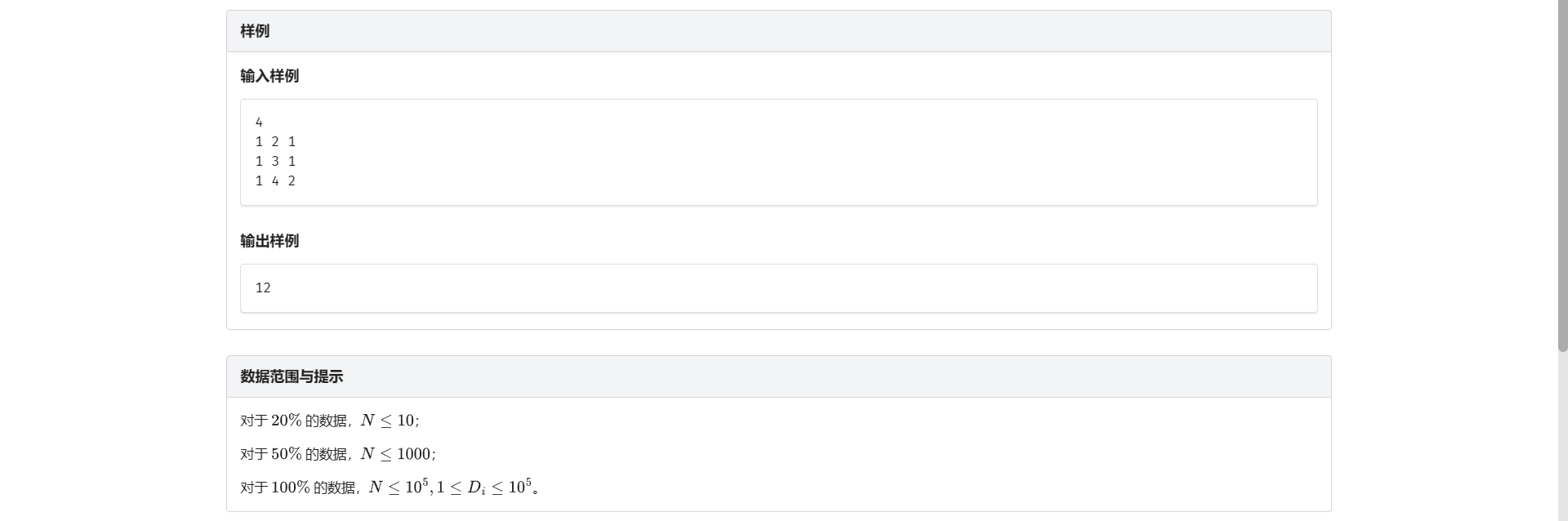
打眼一看感觉无从下手
还是思考性质
注意到“唯一的最小生成树”
那我们想想怎么会让最小生成树不唯一
思考跑 \(kruskal\) 的过程 假如说在同一个权的边集中
将若干个将连通块联通的连法不唯一
那么就会出现最小生成树不唯一的情况
进而考虑 我们连一条边的时候 如果两边的连通块之间还有边权相同的边
那么最小生成树就不唯一了
又因为要求边权最小的完全图 所以别的边边权都应该是该边边权 \(+1\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5 + 0721;
int siz[N], fa[N];
int n;
ll ans;
struct node {
int u, v, w;
friend bool operator<(node a, node b) { return a.w < b.w; }
} edge[N];
int find(int x) {
if (x == fa[x])
return x;
else
return fa[x] = find(fa[x]);
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n - 1; ++i) scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].w);
sort(edge + 1, edge + n);
for (int i = 1; i <= n; ++i) {
siz[i] = 1;
fa[i] = i;
}
for (int i = 1; i <= n - 1; ++i) {
int fx = find(edge[i].u), fy = find(edge[i].v);
if (fx == fy)
continue;
ans += ((ll)siz[fx] * siz[fy] - 1) * (edge[i].w + 1);
siz[fx] += siz[fy];
siz[fy] = 0;
fa[fy] = fx;
ans += edge[i].w;
}
printf("%lld", ans);
return 0;
}
E.连接云朵
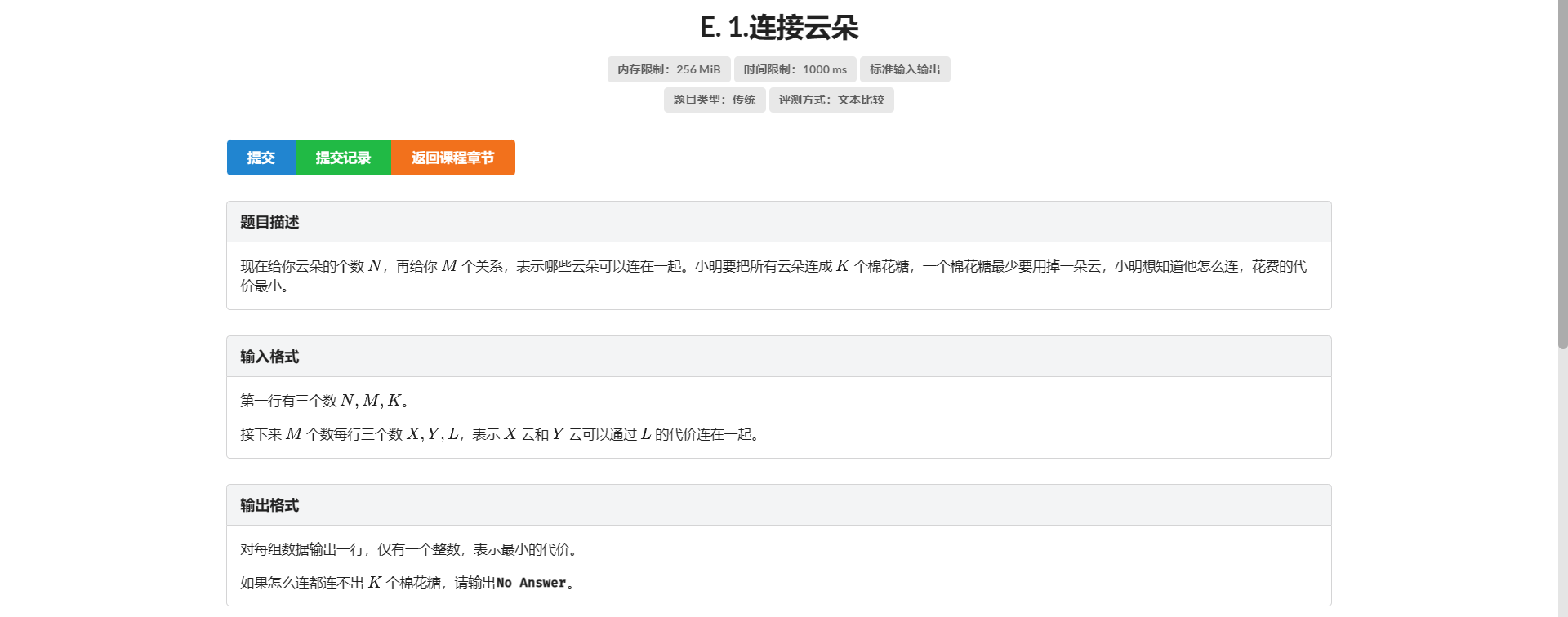
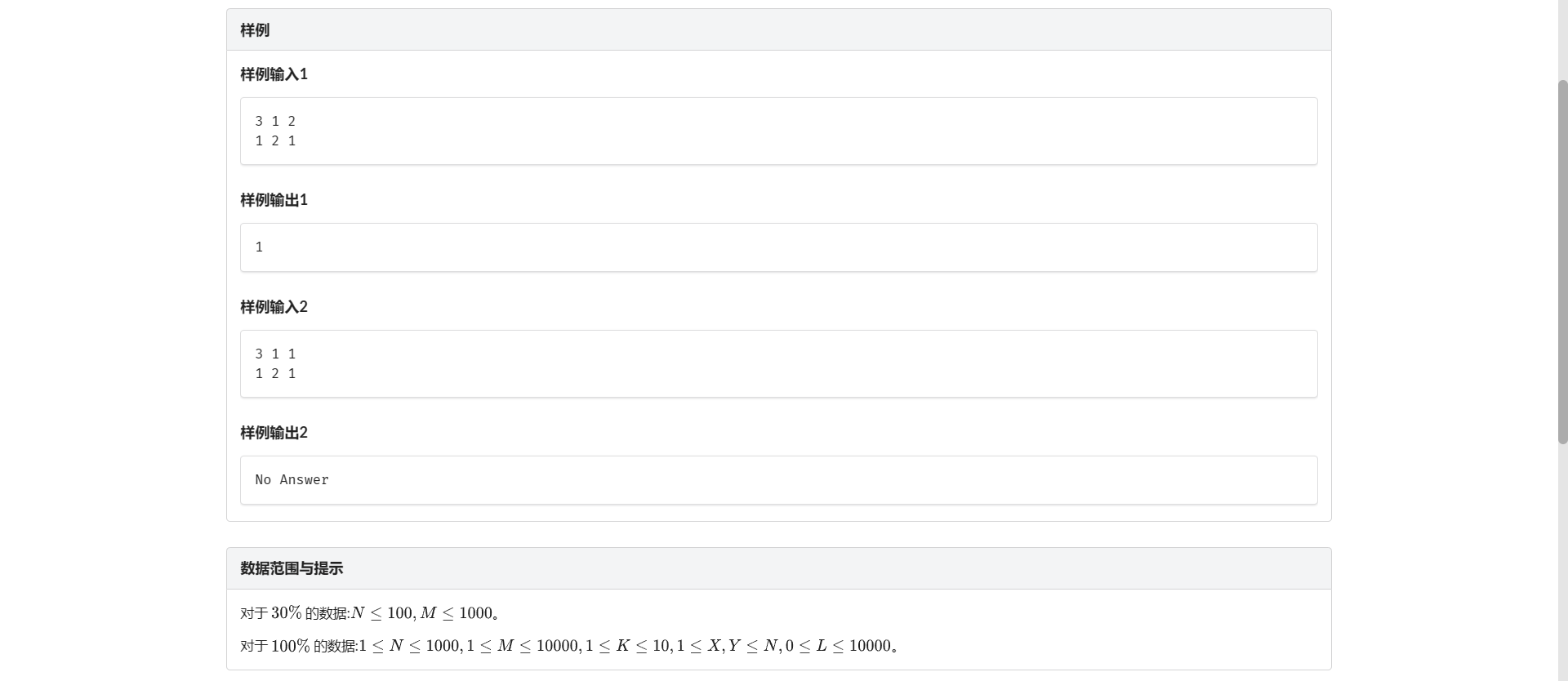
最小生成森林(?
要连接的连通块数量是一定的 所以我们考虑最小化连接的代价
我们发现如果贪心的选取最小的能连接两个连通块的边连接一定是没有问题的
所以本质上和 kruskal 是一样的
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 1e4 + 0721;
int fa[N];
int n, m, k, ans, now;
struct node {
int u, v, w;
friend bool operator<(node x, node y) {
return x.w < y.w;
}
} edge[N];
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n; ++i) fa[i] = i;
for (int i = 1; i <= m; ++i) scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].w);
sort(edge + 1, edge + 1 + m);
now = n;
for (int i = 1; i <= m; ++i) {
int u = edge[i].u, v = edge[i].v;
int fu = find(u), fv = find(v);
if (fu == fv) continue;
fa[fu] = fv;
ans += edge[i].w;
--now;
if (now == k) {
printf("%d\n", ans);
return;
}
}
printf("No Answer\n");
}
}
int main() {
steven24::main();
return 0;
}
/*
3 1 2
1 2 1
*/
F.序列破解
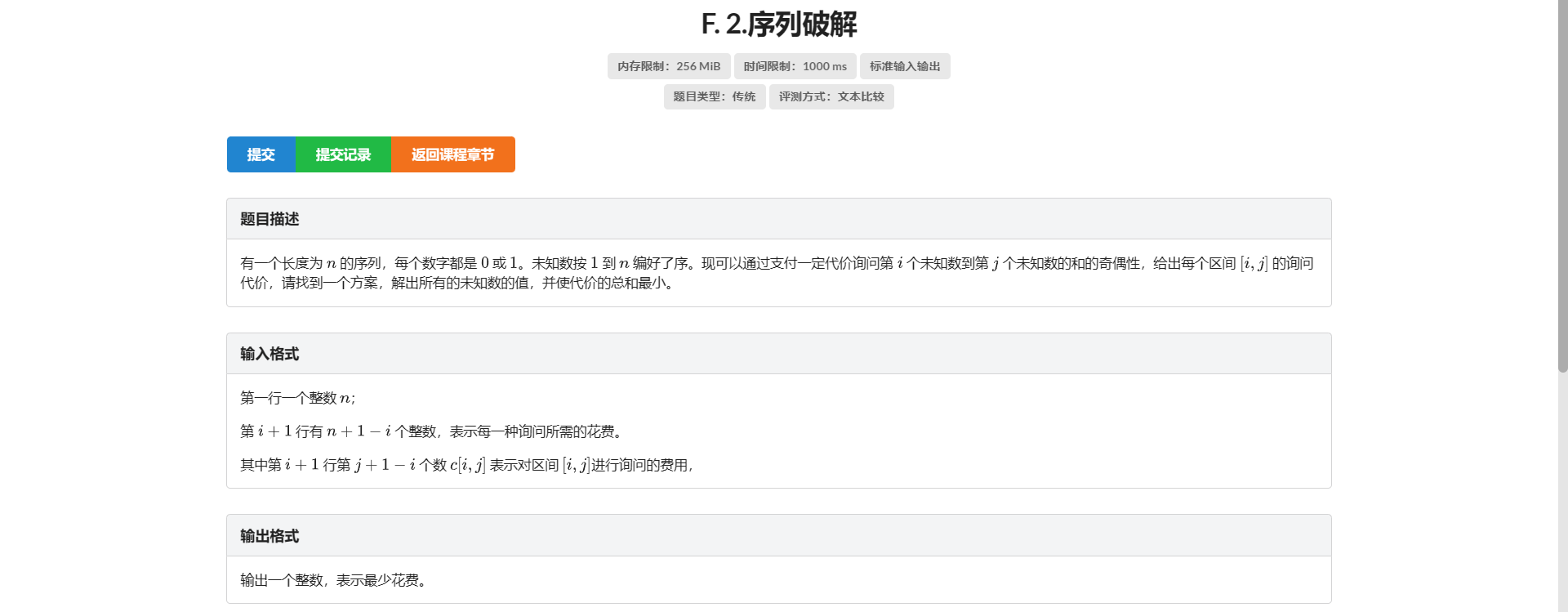
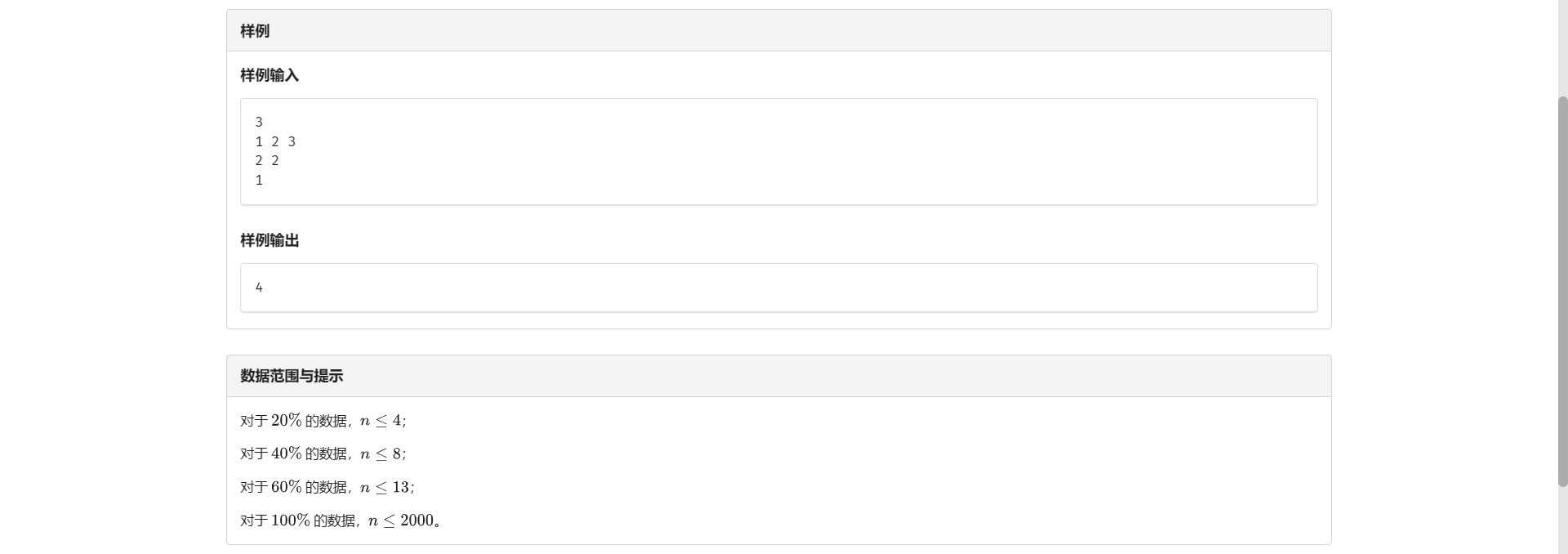
还是那个东西 通过 \(\left[x, y\right]\) 和 \(\left[y, z\right]\) 的询问得到 \(\left[x, z\right]\) 的答案
然后这个东西可以抽象成连边
那么每个位置都已知就代表图联通
那么就转化成了最小生成树
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 0x0d00;
const int M = 4e6 + 0721;
int n;
int a[N][N];
int fa[N];
ll ans;
struct node {
int u, v, w;
friend bool operator<(node x, node y) {
return x.w < y.w;
}
} e[M];
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void main() {
n = read();
for (int i = 0; i <= n; ++i) fa[i] = i;
for (int i = 1; i <= n; ++i) {
for (int j = i; j <= n; ++j) a[i][j] = read();
}
int cnt = 0;
for (int i = 1; i <= n; ++i) {
for (int j = i; j <= n; ++j) {
e[++cnt].u = i - 1;
e[cnt].v = j;
e[cnt].w = a[i][j];
}
}
sort(e + 1, e + 1 + cnt);
for (int i = 1; i <= cnt; ++i) {
int fu = find(e[i].u), fv = find(e[i].v);
if (fu == fv) continue;
ans += e[i].w;
fa[fu] = fv;
}
printf("%lld\n", ans);
}
}
int main() {
steven24::main();
return 0;
}
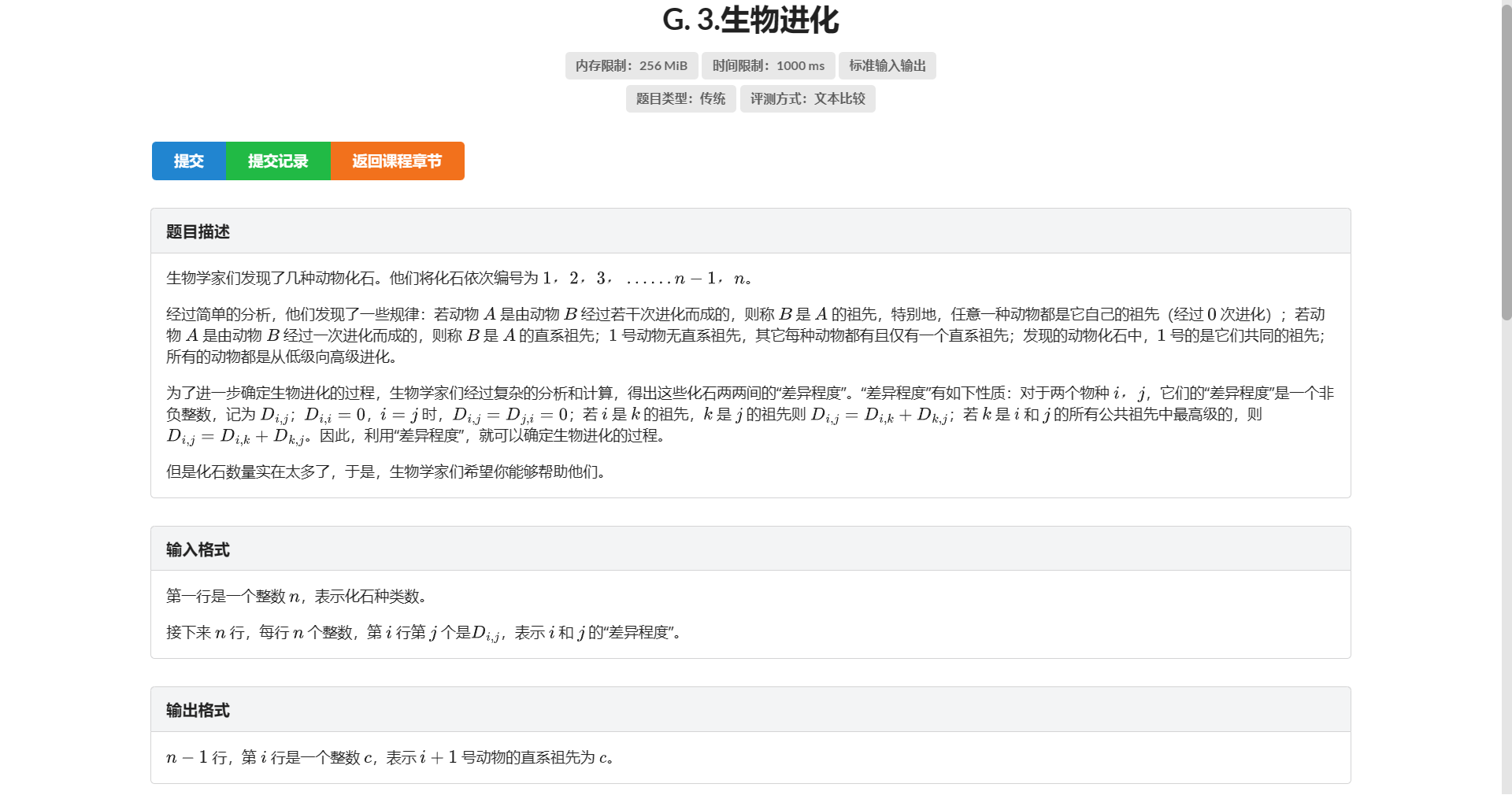
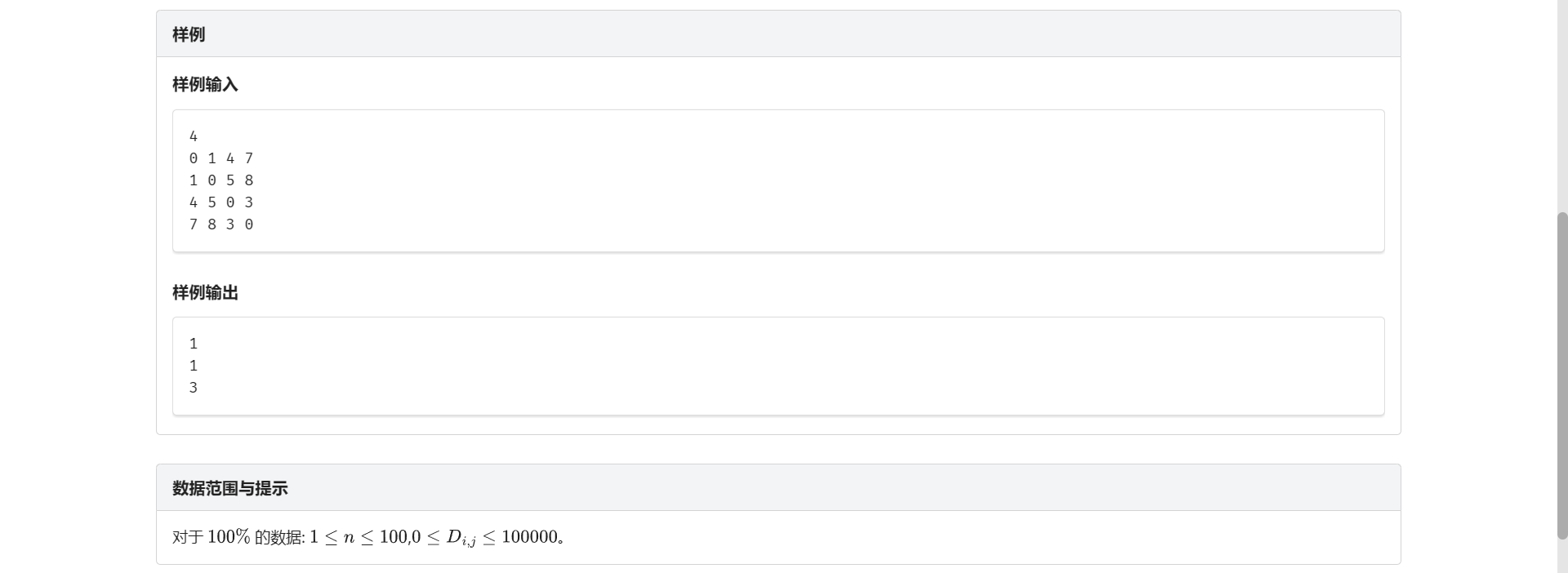
G.生物进化
想了一会 但是做出来了
完全是因为这章是最小生成树才去想的
先说一下做法:根据邻接矩阵把完全图建出来 然后在这个完全图上跑 MST
得到的树即为要求的树
下面是个人的证明(不一定严谨)
首先通过观察可以得出这样一个结论:
对于邻接矩阵中的一条边 \(a_{x, y}\) 一定有 \(\forall z , a_{x, y} \le dis_{x, z} + dis_{z, y}\)
其中 \(dis\) 代表实际树上的距离
然后我们要证明 对于已经联通的 \((x, y)\) 它们树上的距离等于 \(a_{x, y}\)
这个证明分两部分:
- \(dis_{x, y}\) 不可能小于 \(a_{x, y}\)
因为上面的性质 这很显然
- \(dis_{x, y}\) 是这个图中 \(x \rightarrow y\) 的路径中最短的一条
考虑这样一种情况
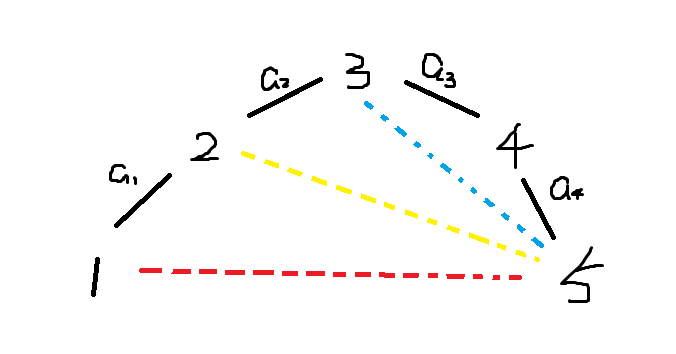
其中我们现在考虑的是那条红边
那么首先我们考虑 \(a_1 + 黄边\)
\(a_1\) 显然是 \(1 \rightarrow 2\) 的最短路
那么如果 \(黄边 = a_2 + a_3 + a_4\) 那么 \(a_2 + a_3 + a_4\) 就是 \(2 \rightarrow 5\) 的最短路
那么 \(1 \rightarrow 5\) 就是原图中的最短路
然后我们递归的考虑黄边和蓝边 发现最终一定能落在一条实边上 此结论成立
进而证毕
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 0x0d00;
const int M = 4e6 + 0721;
int n;
int a[N][N];
int fa[N], f[N];
int head[N], nxt[N << 1], to[N << 1], cnt;
struct node {
int u, v, w;
friend bool operator<(node x, node y) {
return x.w < y.w;
}
} e[M];
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void dfs(int x, int ff) {
f[x] = ff;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == ff) continue;
dfs(y, x);
}
}
void main() {
n = read();
for (int i = 1; i <= n; ++i) fa[i] = i;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) a[i][j] = read();
}
cnt = 0;
for (int i = 1; i <= n; ++i) {
for (int j = i; j <= n; ++j) {
e[++cnt].u = i;
e[cnt].v = j;
e[cnt].w = a[i][j];
}
}
sort(e + 1, e + 1 + cnt);
for (int i = 1; i <= cnt; ++i) {
int fu = find(e[i].u), fv = find(e[i].v);
if (fu == fv) continue;
add_edge(e[i].u, e[i].v);
add_edge(e[i].v, e[i].u);
fa[fu] = fv;
}
dfs(1, 0);
for (int i = 2; i <= n; ++i) printf("%d\n", f[i]);
}
}
int main() {
steven24::main();
return 0;
}
/*
4
0 1 4 7
1 0 5 8
4 5 0 3
7 8 3 0
*/
H.保留道路
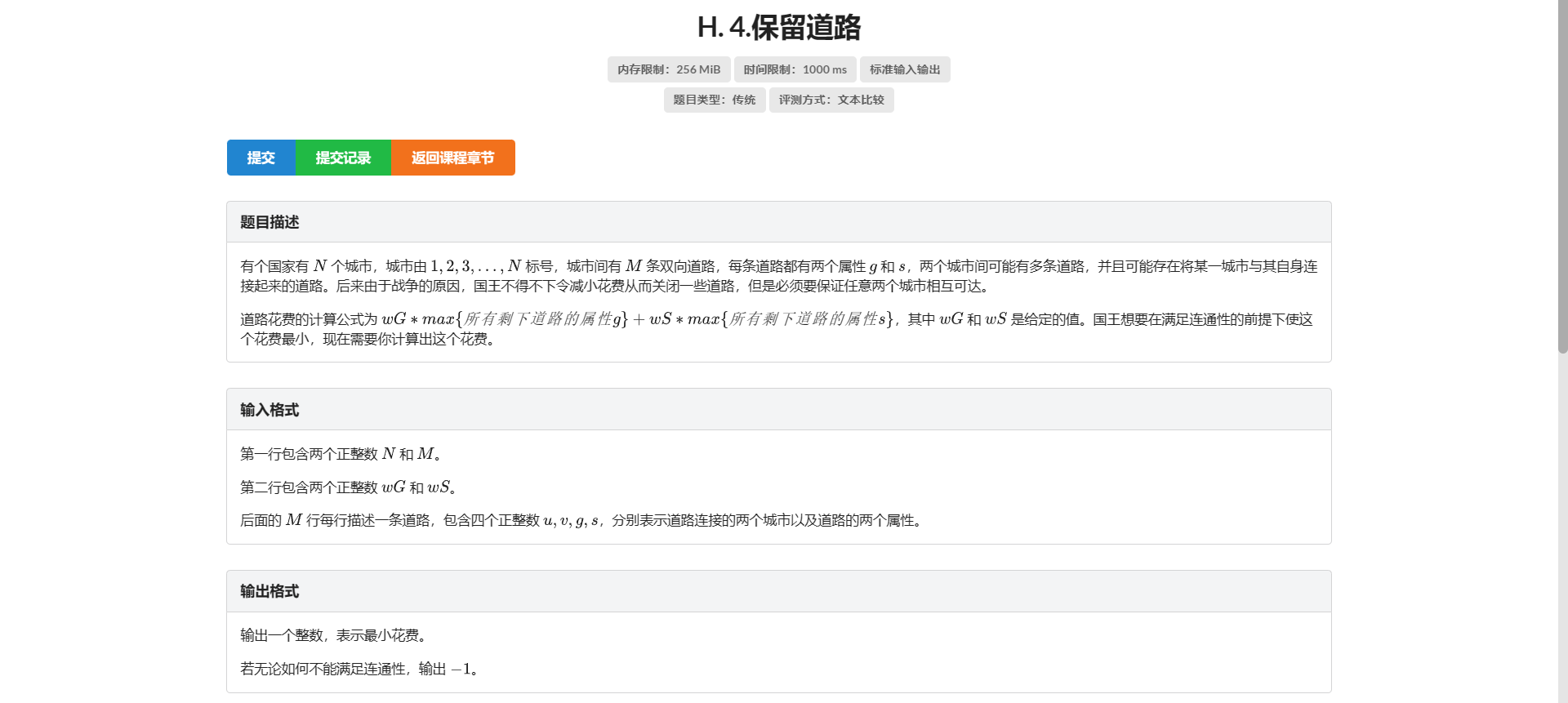
最开始想到对 \(g\) 二分 结果发现答案是个类似于二次函数的抛物线状
思考 wqs 二分 无果
对于这种二维的东西 很常见的想法是先对一维排序让其有序再考虑另一维
那么我们先对 \(g\) 进行排序
那么我们现在要做的就是挨个加边 然后把加进来的边按 \(s\) 进行排序跑一次 kruskal
进而发现每次加边的过程可以用那个经典的冒泡来优化复杂度
并且实质上每次我们只需要考虑当前在 MST 上的 \(n - 1\) 条边和新加进来那条边 所以边集大小控制在 \(n\) 即可
这样复杂度就是 \(\text{O} (nm)\)
写的时候忘了前 \(n - 1\) 条边不一定保证联通 挂了 10 分 不是为啥就这还能过 90 啊
还有此题没有 -1 的点 忘写了也能过(
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int M = 5e4 + 0721;
const int N = 521;
int fa[N];
int n, m;
int WG, WS;
int del;
ll ans = 0x7ffffffffffffff;
struct node {
int u, v, g, s;
} e[M], kl[N];
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline bool cmp1(node x, node y) {
return x.g < y.g;
}
inline bool cmp2(node x, node y) {
return x.s < y.s;
}
void init() {
for (int i = 1; i <= n; ++i) fa[i] = i;
}
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void kruskal(int top) {
init();
int maxg = 0, maxs = 0;
int cnt = n - 1;
for (int i = 1; i <= top; ++i) {
int fu = find(kl[i].u), fv = find(kl[i].v);
if (fu == fv) {
del = i;
continue;
}
maxg = max(maxg, kl[i].g), maxs = max(maxs, kl[i].s);
fa[fu] = fv;
--cnt;
}
if (!cnt) ans = min(ans, 1ll * maxg * WG + 1ll * maxs * WS);
}
void main() {
n = read(), m = read();
WG = read(), WS = read();
for (int i = 1; i <= m; ++i) e[i].u = read(), e[i].v = read(), e[i].g = read(), e[i].s = read();
sort(e + 1, e + 1 + m, cmp1);
for (int i = 1; i < n; ++i) kl[i] = e[i];
sort(kl + 1, kl + n, cmp2);
kruskal(n - 1);
for (int i = n; i <= m; ++i) {
int tmp = n;
kl[tmp] = e[i];
while (kl[tmp].s < kl[tmp - 1].s && tmp >= 1) {
swap(kl[tmp], kl[tmp - 1]);
--tmp;
}
kruskal(n);
for (int j = del; j < n; ++j) swap(kl[j], kl[j + 1]);
}
if (ans != 0x7ffffffffffffff) printf("%lld\n", ans);
else printf("-1\n");
}
}
int main() {
steven24::main();
return 0;
}
/*
3 3
2 1
1 2 10 15
1 2 4 20
1 3 5 1
*/
I.最小距离和
考虑乱搞 我们不把 \(O(n^2)\) 条边全建出来
我们首先按 \(x\) 排序 对于每个点把它分别和它后面 10 个点连边
然后按 \(y\) 排序 对于每个点把它分别和它后面 10 个点连边
最后按 \(z\) 排序 对于每个点把它分别和它后面 10 个点连边
这样我们就会得到 \(3 \times 10^6\) 条边(实际因为边界问题会比这少一丢丢)
然后跑 kruskal
然后就过了(?
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 1e5 + 0721;
const int M = 3e6 + 0721;
int n;
int fa[N];
int cnt;
ll ans;
struct dot {
int x, y, z, id;
} a[N];
struct edge {
int u, v, w;
friend bool operator<(edge x, edge y) {
return x.w < y.w;
}
} e[M];
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
inline bool cmpx(dot x, dot y) {
if (x.x != y.x) return x.x < y.x;
else if (x.y != y.y) return x.y < y.y;
else return x.z < y.z;
}
inline bool cmpy(dot x, dot y) {
if (x.y != y.y) return x.y < y.y;
else if (x.x != y.x) return x.x < y.x;
else return x.z < y.z;
}
inline bool cmpz(dot x, dot y) {
if (x.z != y.z) return x.z < y.z;
else if (x.x != y.x) return x.x < y.x;
else return x.y < y.y;
}
int calc(dot x, dot y) {
return min(abs(x.x - y.x), min(abs(x.y - y.y), abs(x.z - y.z)));
}
void init() {
for (int i = 1; i <= n; ++i) fa[i] = i;
}
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void kruskal() {
init();
sort(e + 1, e + 1 + cnt);
for (int i = 1; i <= cnt; ++i) {
int fu = find(e[i].u), fv = find(e[i].v);
if (fu == fv) continue;
ans += e[i].w;
fa[fu] = fv;
}
}
void main() {
n = read();
for (int i = 1; i <= n; ++i) {
a[i].x = read(), a[i].y = read(), a[i].z = read();
a[i].id = i;
}
sort(a + 1, a + 1 + n, cmpx);
for (int i = 1; i <= n; ++i) {
for (int j = 1; i + j <= n && j <= 10; ++j) {
e[++cnt].u = a[i].id;
e[cnt].v = a[i + j].id;
e[cnt].w = calc(a[i], a[i + j]);
}
}
sort(a + 1, a + 1 + n, cmpy);
for (int i = 1; i <= n; ++i) {
for (int j = 1; i + j <= n && j <= 10; ++j) {
e[++cnt].u = a[i].id;
e[cnt].v = a[i + j].id;
e[cnt].w = calc(a[i], a[i + j]);
}
}
sort(a + 1, a + 1 + n, cmpz);
for (int i = 1; i <= n; ++i) {
for (int j = 1; i + j <= n && j <= 10; ++j) {
e[++cnt].u = a[i].id;
e[cnt].v = a[i + j].id;
e[cnt].w = calc(a[i], a[i + j]);
}
}
kruskal();
printf("%lld\n", ans);
}
}
int main() {
steven24::main();
return 0;
}
/*
3
-1 -1 -1
5 5 5
10 10 10
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号