YBTOJ 2.5AC自动机
A.单词查询
AC自动机板子
大致讲一下AC自动机是什么东西
首先我们把匹配的若干个串插到 \(trie\) 树里
然后把要匹配的串放到树里跑
显然 我们是不能暴力跑的 所以要构建失配指针
假如说我这个节点是父节点连了条字母为 \(s\) 的边
那么这个节点的失配指针就要指到它父亲的失配指针指向的节点的连向 \(s\) 的节点
如果没有 就找到 \(fail\) 的 \(fail\) 直到找到有这么个儿子
如果跳到根节点还没找到 那就连到根节点
这里还有个优化 如果一个父亲 它没有这个儿子 那就把这个儿子指向它的 \(fail\) 指针的这个儿子
这样的话我们就省去了暴力跳 \(fail\) 指针直到直到找到儿子的过程
并且由于 \(fail\) 指针肯定是由下指到上的 所以采用 \(BFS\) 一层一层构建
这部分代码就是
void build(void) {
queue<int>q;
int p = 0;
for (int i = 0; i < 26; ++i) {
if (ch[p][i])
q.push(ch[p][i]);
}
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = 0; i < 26; ++i) {
if (ch[now][i]) {
fail[ch[now][i]] = ch[fail[now]][i];
q.push(ch[now][i]);
} else
ch[now][i] = ch[fail[now]][i];
}
}
}
具体查询代码实际上是因题而异的
比如这题 要查一共出现了多少种单词
那么我们建树的时候 把每个单词结尾对应的节点都打上一个 \(ed\) 标
然后把文本串放到自动机里跑的时候 每到一个格都要暴力跳 \(fail\) 记录可能会出现的单词
说起来有点抽象 实际上就长这样
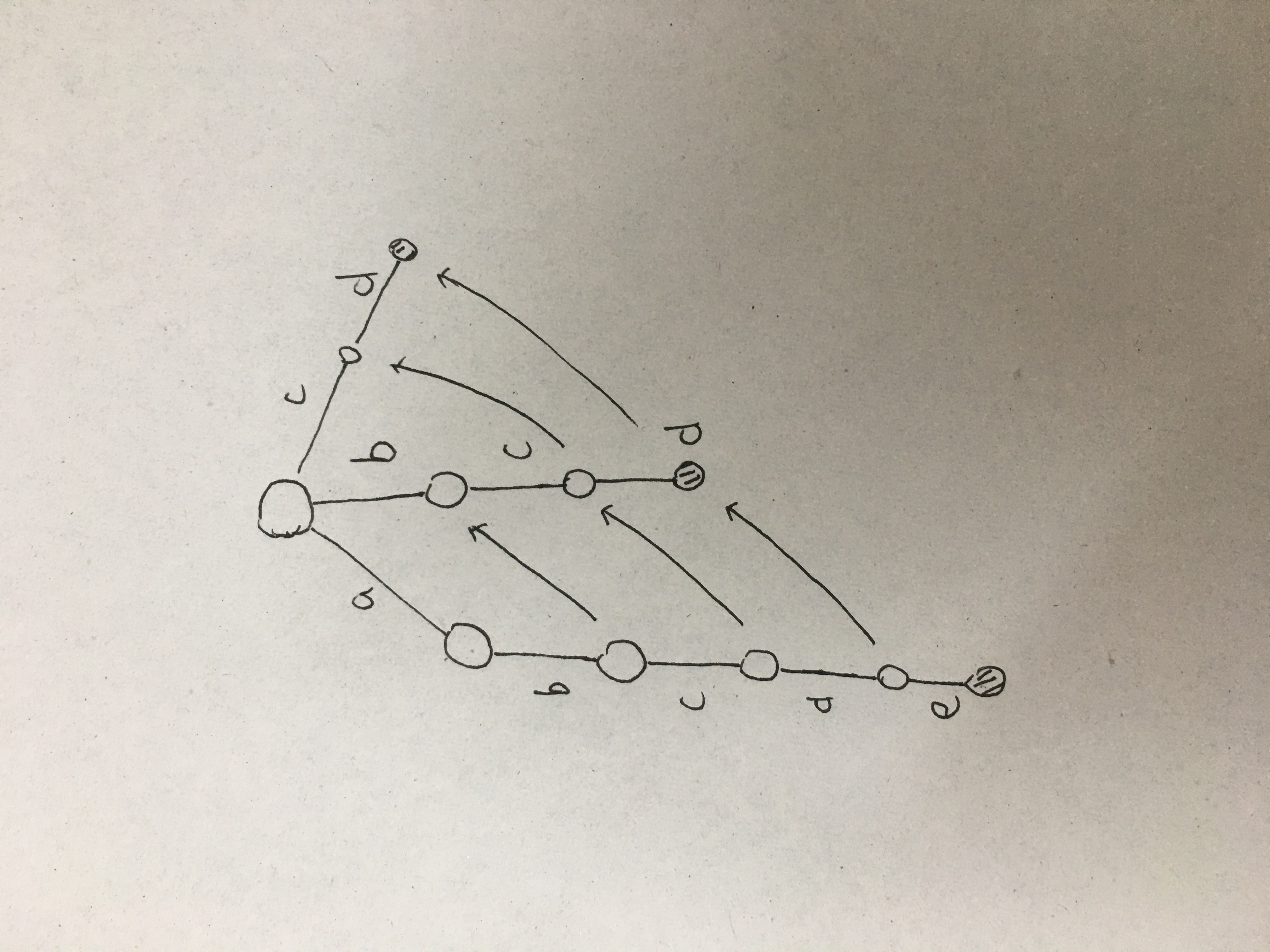
因为我们只需要统计一次 所以跳过的就打个标记 下次就不再跳了
就不会因为暴力跳而导致 \(TLE\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 0721;
int tr[N][26], ed[N], fail[N], tot;
void insert(string s) {
int u = 0;
for (int i = 0; i < s.length(); ++i) {
if (!tr[u][s[i] - 'a'])
tr[u][s[i] - 'a'] = ++tot;
u = tr[u][s[i] - 'a'];
}
++ed[u];
}
queue<int> q;
void build(void) {
for (int i = 0; i < 26; ++i) {
if (tr[0][i]) q.push(tr[0][i]);
}
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < 26; ++i) {
if (tr[u][i]) {
fail[tr[u][i]] = tr[fail[u]][i];
q.push(tr[u][i]);
} else
tr[u][i] = tr[fail[u]][i];
}
}
}
int query(string s) {
int res = 0, u = 0;
for (int i = 0; i < s.length(); ++i) {
u = tr[u][s[i] - 'a'];
for (int j = u; j && ed[j] != -1; j = fail[j]) {
res += ed[j];
ed[j] = -1;
}
}
return res;
}
int main() {
ios::sync_with_stdio(false);
int T;
cin >> T;
while (T--) {
int n;
cin >> n;
memset(tr, 0, sizeof tr );
memset(fail, 0, sizeof fail);
memset(ed, 0, sizeof ed );
for (int i = 1; i <= n; ++i) {
string s;
cin >> s;
insert(s);
}
build();
string s;
cin >> s;
cout << query(s) << endl;
}
return 0;
}
当然对于下面这道题 暴力跳可能就不太行了。。。
B.单词频率
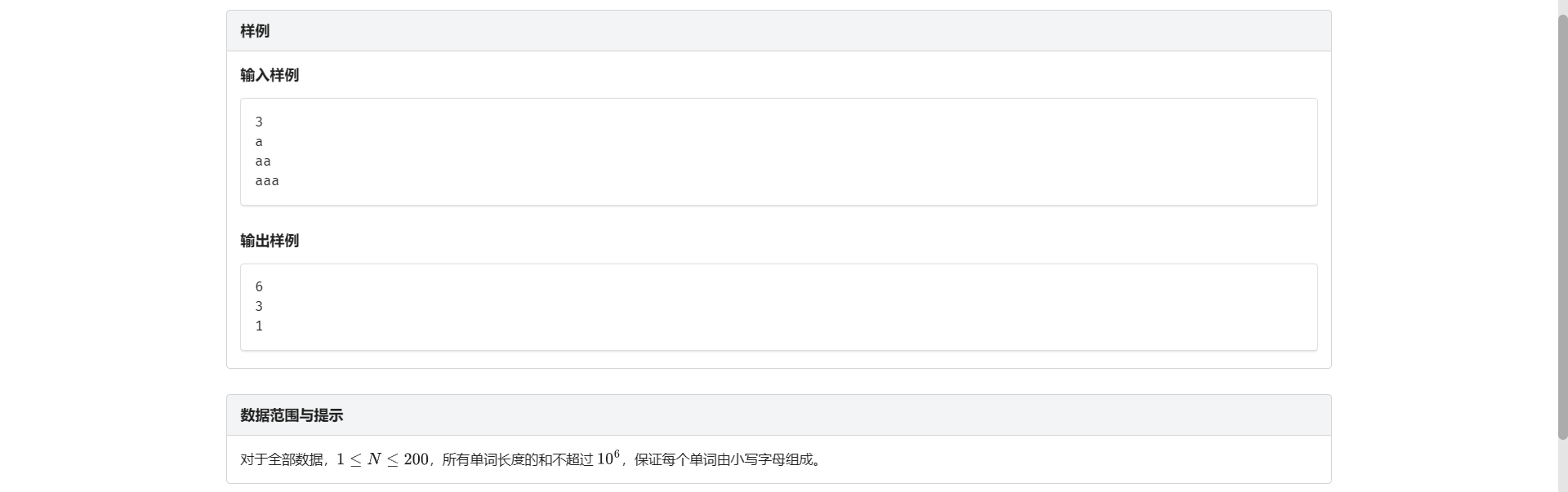
做过上面那题 其实这题思路就简单了 暴力跳 只不过不需要打标
然后交了一发狠狠的T掉了
那我们思考一下怎么优化
那肯定是优化暴力跳的过程嘛
然后想一想怎么跳的 发现每次都是从当前节点一路跳到根节点
也就是说 如果当前节点走到一次 它后面连接 \(fail\) 的节点都会被经过一次
那么是不是就说明 我们可以不用每次都暴力跳 直接记录当前这个点被经过了多少次
最后把它后面连接 \(fail\) 的节点都加上这个次数即可
因为失配指针的存储是类似于单向链表的一个结构 想到图 那么对于所有的点 如果把失配指针都看作一条有向边 就会发现统计答案变成了一个在 \(DAG\) 上的 \(DP\)
然后再想 因为最后都要跳回根节点 那么实际上这个 \(DAG\) 的终点是唯一的
并且因为从一个点出发只有一条边(即一个 \(fail\) 指针)连出
那我们如果反向建边 这个图就是一颗树
那么统计答案就是一个树形 \(DP\) 了
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 0721;
int ch[N][26], fail[N], sum[N], id[N], tot;
int head[N], to[N], nxt[N], cnt;
int n;
inline void cmb(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void insert(int x) {
string s;
cin >> s;
int p = 0;
for (int i = 0; i < s.length(); ++i) {
int c = s[i] - 'a';
if (!ch[p][c]) ch[p][c] = ++tot;
p = ch[p][c];
++sum[p];
}
id[x] = p;
}
void build(void) {
queue<int> q;
for (int i = 0; i < 26; ++i) {
if (ch[0][i]) q.push(ch[0][i]);
}
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = 0; i < 26; ++i) {
if (ch[now][i]) fail[ch[now][i]] = ch[fail[now]][i], q.push(ch[now][i]);
else ch[now][i] = ch[fail[now]][i];
}
}
}
void build_fail(void) {
for (int i = 1; i <= tot; ++i) cmb(fail[i], i);
}
void dfs(int x) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
dfs(y);
sum[x] += sum[y];
}
}
int main() {
ios::sync_with_stdio(false);
cin >> n;
for (int i = 1; i <= n; ++i) insert(i);
build();
build_fail();
dfs(0);
for (int i = 1; i <= n; ++i) cout << sum[id[i]] << endl;
return 0;
}
C.前缀匹配
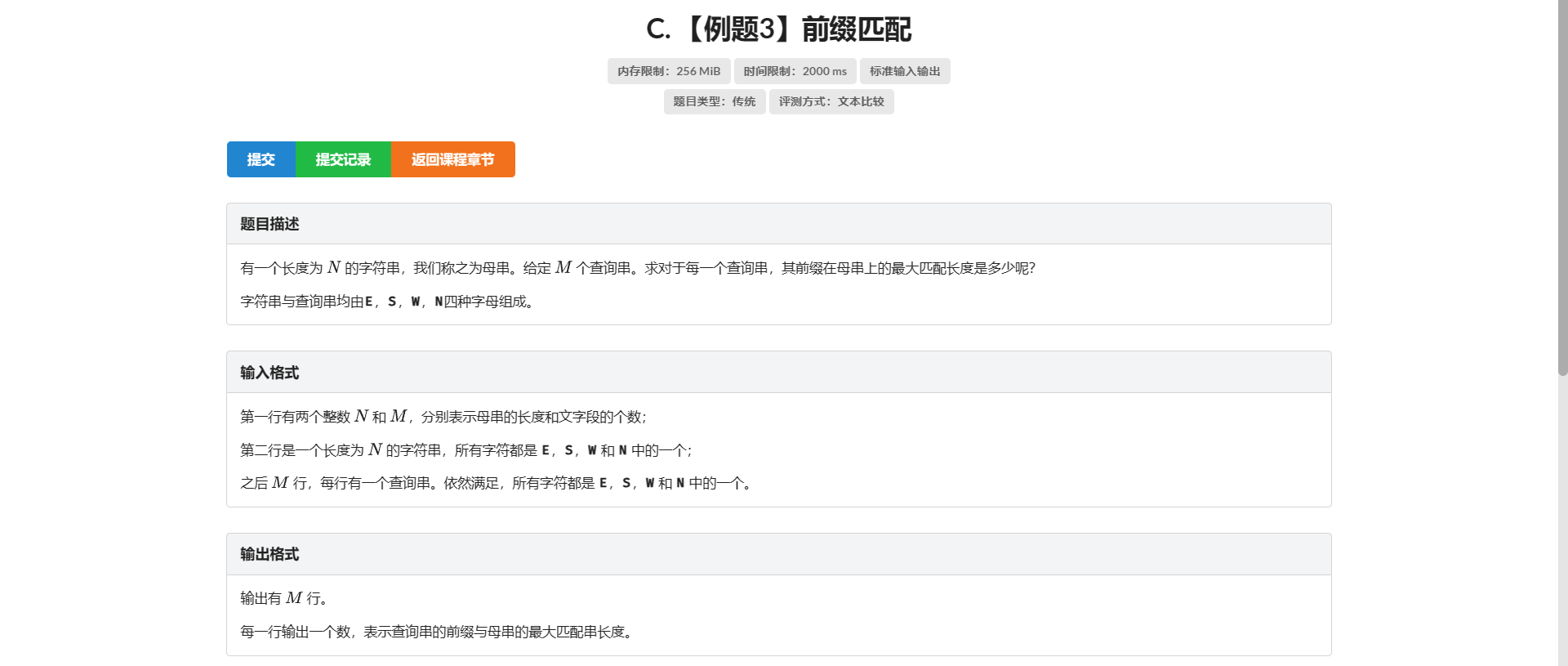
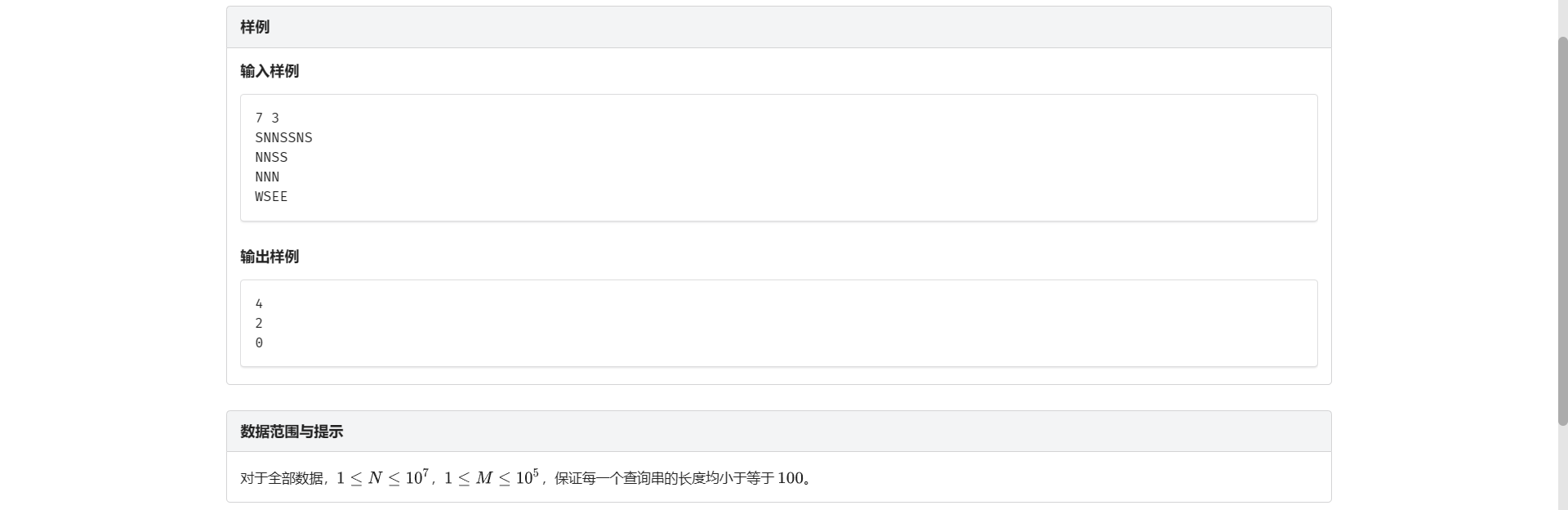
经过了前两道题的摧残历练 这题显然就显得非常非常的友善了
就我们把文本串放里面跑一遍 然后查模式串在里面被走到的最远的地方就行
因为就要查走没走过嘛 所以暴力跳然后打标显然就能过
当然你要建 \(fail\) 树然后统计这个点被经历次数为不为 \(0\) 显然也行
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e7 + 0721;
const int M = 1e5 + 0721;
int ch[N][4], fail[N], tot;
bool vis[N], sum[N];
string s[M];
string s1;
int n, m;
int getnum(char c) {
if (c == 'E') return 0;
else if (c == 'S') return 1;
else if (c == 'W') return 2;
else return 3;
}
void insert(string ss) {
int p = 0;
for (int i = 0; i < ss.length(); ++i) {
int c = getnum(ss[i]);
if (!ch[p][c]) ch[p][c] = ++tot;
p = ch[p][c];
}
}
void build(void) {
queue<int> q;
for (int i = 0; i < 4; ++i) {
if (ch[0][i])
q.push(ch[0][i]);
}
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = 0; i < 4; ++i) {
if (ch[now][i]) fail[ch[now][i]] = ch[fail[now]][i], q.push(ch[now][i]);
else ch[now][i] = ch[fail[now]][i];
}
}
}
void query(string ss) {
int p = 0;
for (int i = 0; i < ss.length(); ++i) {
int c = getnum(ss[i]);
p = ch[p][c];
for (int j = p; j && !vis[j]; j = fail[j]) vis[j] = 1;
}
}
int getans(string ss) {
int p = 0;
int ans = 0;
for (int i = 0; i < ss.length(); ++i) {
int c = getnum(ss[i]);
if (vis[ch[p][c]]) {
++ans;
p = ch[p][c];
} else
break;
}
return ans;
}
int main() {
ios::sync_with_stdio(false);
cin >> n >> m;
cin >> s1;
for (int i = 1; i <= m; ++i) {
cin >> s[i];
insert(s[i]);
}
build();
query(s1);
for (int i = 1; i <= m; ++i) cout << getans(s[i]) << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号