YBTOJ 2.4字典树
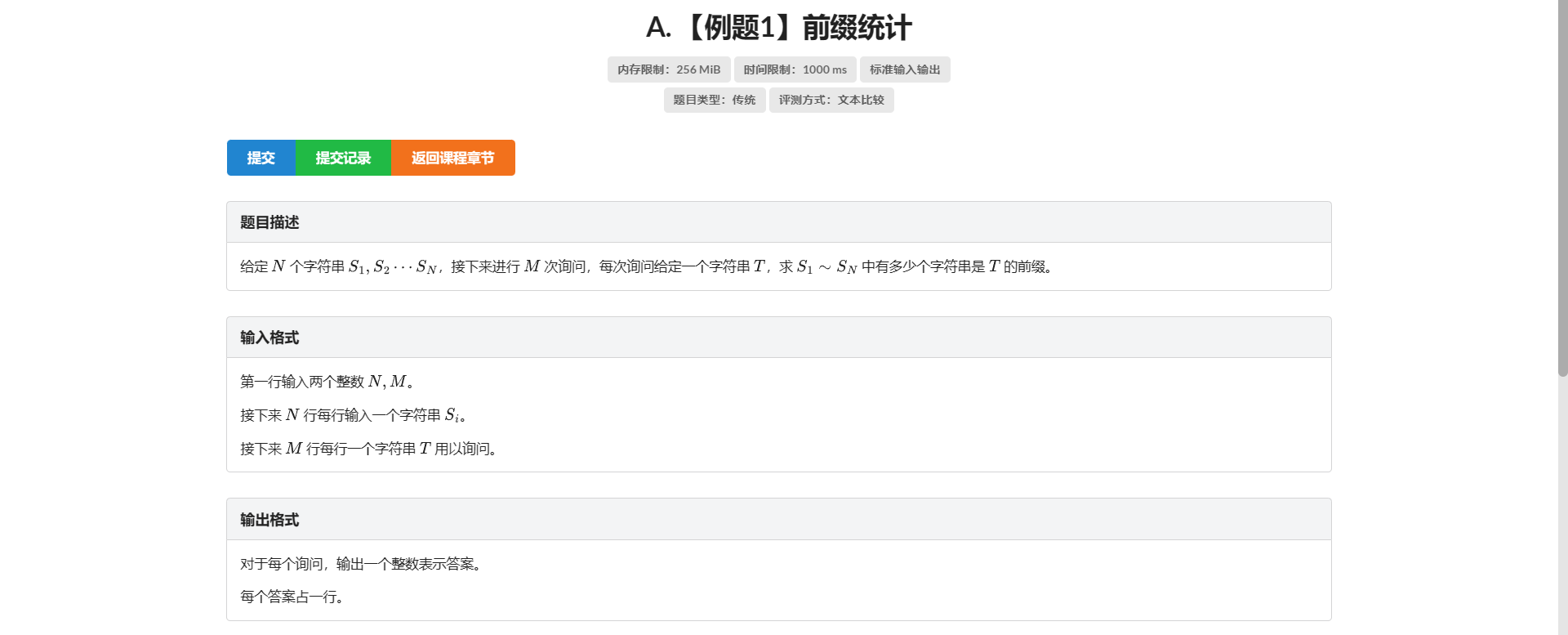
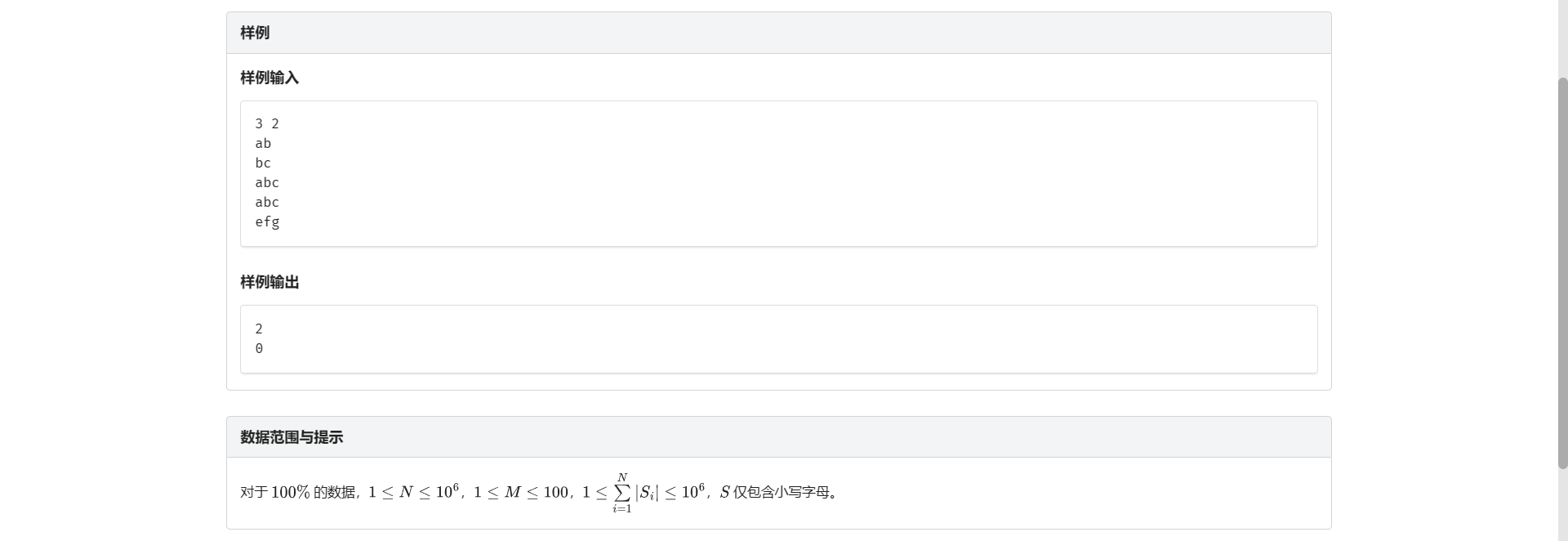
A.前缀统计
字典树 顾名思义就是做一个类似于字典的树
根节点往下连边 每条边代表一个字母
对于插入操作 我们从根节点出发往下走
如果有对应的字母边 就继续走到对应的儿子节点
如果没有 就新建一个节点
查询同理 按字母边往下走即可
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 3e6 + 0721;
int tr[N][70], en[N], cnt;
int n, q, T;
int getnum(char c) {
if (c >= 'A' && c <= 'Z')
return c - 'A';
else if (c >= 'a' && c <= 'z')
return c + 26 - 'a';
else
return c - '0' + 52;
}
void build(string s) {
int len = s.length();
int now = 0;
for (int i = 0; i < len; ++i) {
int x = getnum(s[i]);
if (!tr[now][x])
tr[now][x] = ++cnt;
// en[tr[now][x]]++ ;
now = tr[now][x];
}
en[now]++;
}
int query(string s) {
int sum = 0;
int len = s.length();
int now = 0;
for (int i = 0; i < len; ++i) {
int x = getnum(s[i]);
if (!tr[now][x])
return sum;
else
now = tr[now][x], sum += en[now];
}
return sum;
}
int main() {
// scanf("%d" ,&T ) ;
// while(T--){
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; ++i) {
string s;
cin >> s;
build(s);
}
for (int i = 1; i <= q; ++i) {
string s;
cin >> s;
printf("%d\n", query(s));
}
return 0;
}
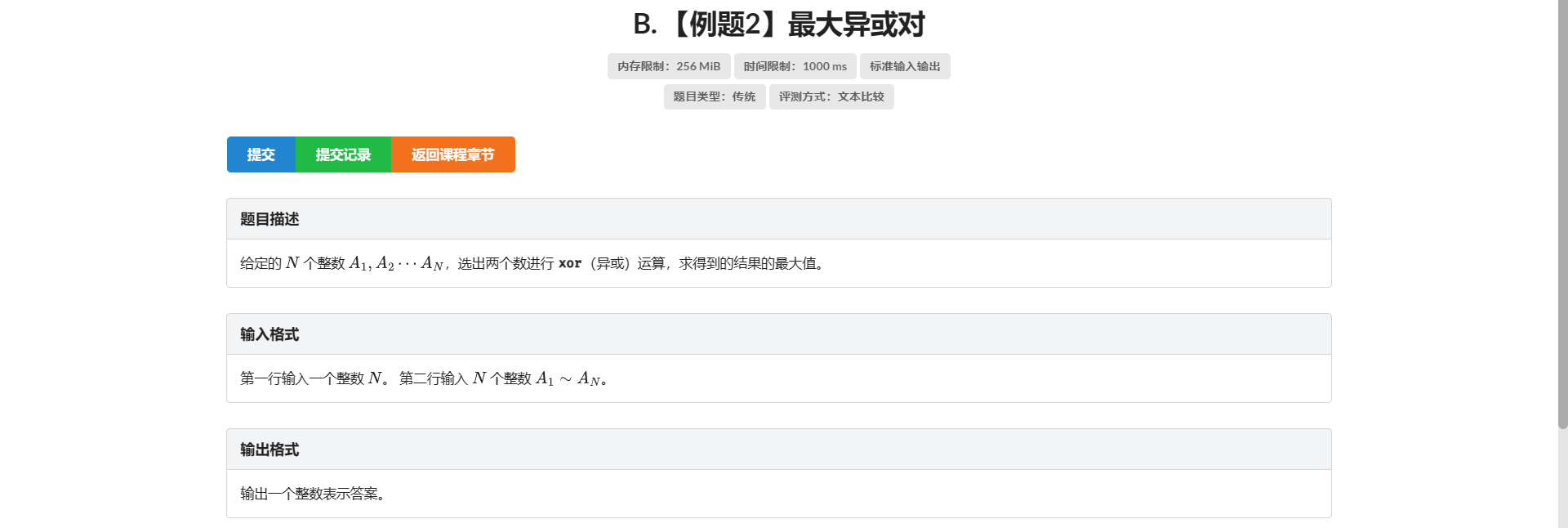
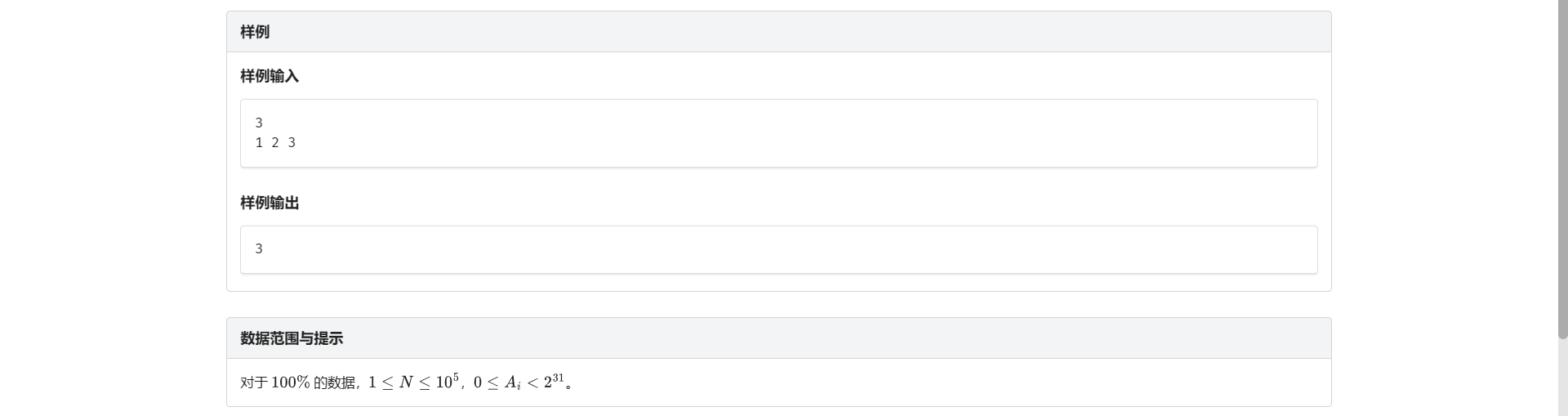
B.最大异或对
看到最大异或 考虑 \(01trie\)
因为 \(100000\) 显然大于 \(011111\) 我们贪心的让高位尽可能是 \(1\) 即可
看到 \(10^5\) 的数据范围 发现枚举其中一个数字 然后查询对应的能达到最大异或的另一个数字即可
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
int a[N];
int tr[10000721][2];
int n, cnt, ans;
void build(int x) {
int now = 0;
for (int i = 1 << 30; i > 0; i = i >> 1) {
bool wei = i & x;
if (!tr[now][wei])
tr[now][wei] = ++cnt;
now = tr[now][wei];
// cout<<i<<" ";
}
}
int query(int x) {
int sum = 0, now = 0;
for (int i = 1 << 30; i > 0; i = i >> 1) {
bool wei = i & x;
if (tr[now][!wei]) {
sum += i;
now = tr[now][!wei];
}
else
now = tr[now][wei];
// cout<<"1";
}
return sum;
}
int main() {
scanf("%d",&n);
for (int i = 1; i <= n; ++i) {
scanf("%d",&a[i]);
build(a[i]);
}
for (int i = 1; i <= n; ++i) {
ans = max(ans , query(a[i]));
}
printf("%d",ans);
return 0;
}
C.最长异或路径
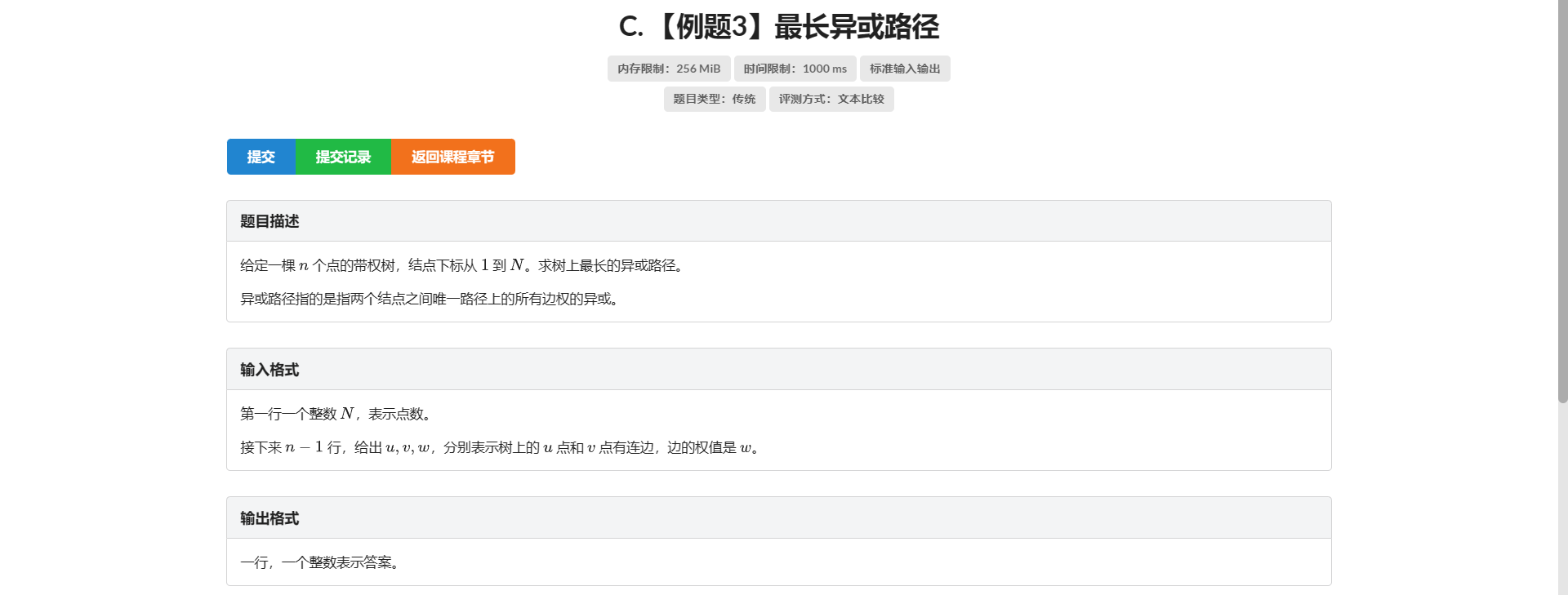
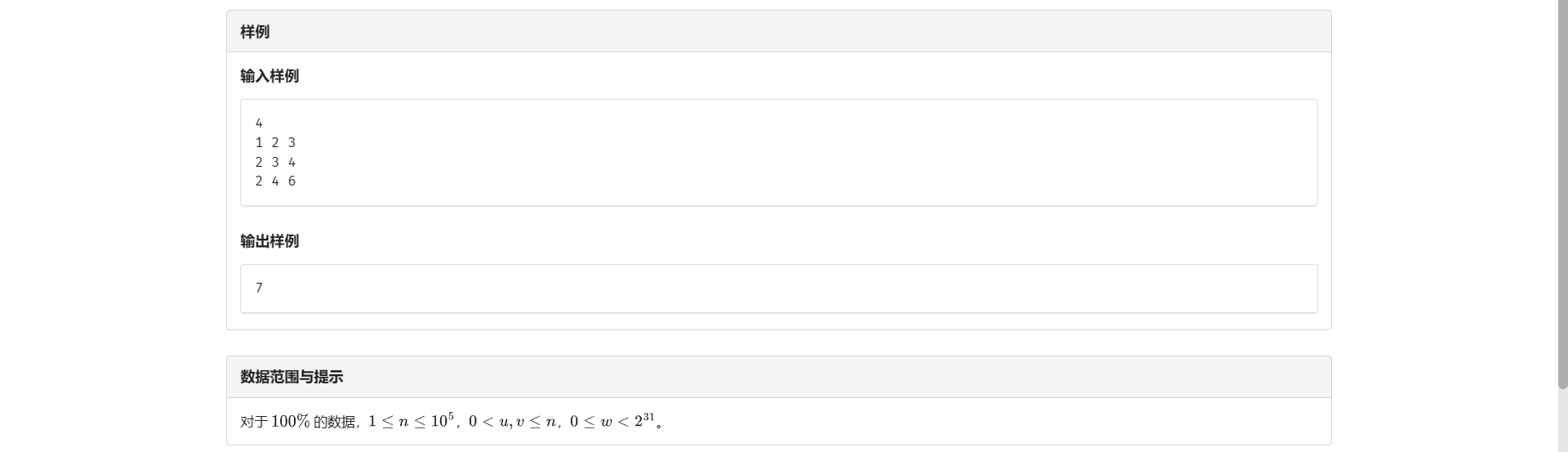
还是思考特殊性质 首先这题要做的第一件事就是要整明白怎么统计路径
然后就会非常自然的想到 \(LCA\)
但是要枚举点对的话 复杂度就是 \(O(n^2logn)\)
这不直接T飞!
看看有什么怪异的特殊条件 看到了异或
思考一下异或(特别是异或和)有什么特殊的性质
然后我们发现异或一个数两次跟没异或是一样的
那我们还是考虑长 \(LCA\) 模样的路径统计 发现 \(LCA\) 到根节点的异或和会重复
那就相当于没异或
这样由 \(i\) 到 \(j\) 的异或和就是 \(i\) 和 \(j\) 到根节点的异或和异或起来
然后我们就发现枚举一个端点的时候另一个端点可以直接在 \(01trie\) 上跑
然后就和上一题一样了
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2000001;
int head[N], nxt[N], v[N], to[N], cnt;
int sum[N];
int tr[N][2], tot;
int ans;
int n;
void cmb(int x, int y, int z) {
to[++cnt] = y;
v[cnt] = z;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x, int fa) {
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa)
continue;
sum[y] = sum[x] ^ v[i];
dfs(y, x);
}
}
void built(int val, int x) {
for (int i = 30; i >= 0; i--) {
int wei = (val >> i) & 1;
// cout<<wei ;
if (tr[x][wei] == 0)
tr[x][wei] = ++tot;
x = tr[x][wei];
}
}
int cx(int val, int x) {
int re = 0;
for (int i = 30; i >= 0; i--) {
int wei = (val >> i) & 1;
// cout<<wei ;
if (tr[x][!wei] != 0) {
re += (1 << i);
x = tr[x][!wei];
} else
x = tr[x][wei];
}
return re;
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; ++i) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
cmb(x, y, z);
cmb(y, x, z);
}
dfs(1, -1);
for (int i = 1; i <= n; ++i) built(sum[i], 0);
for (int i = 1; i <= n; ++i) ans = max(ans, cx(sum[i], 0));
printf("%d", ans);
return 0;
}
D.阅读理解
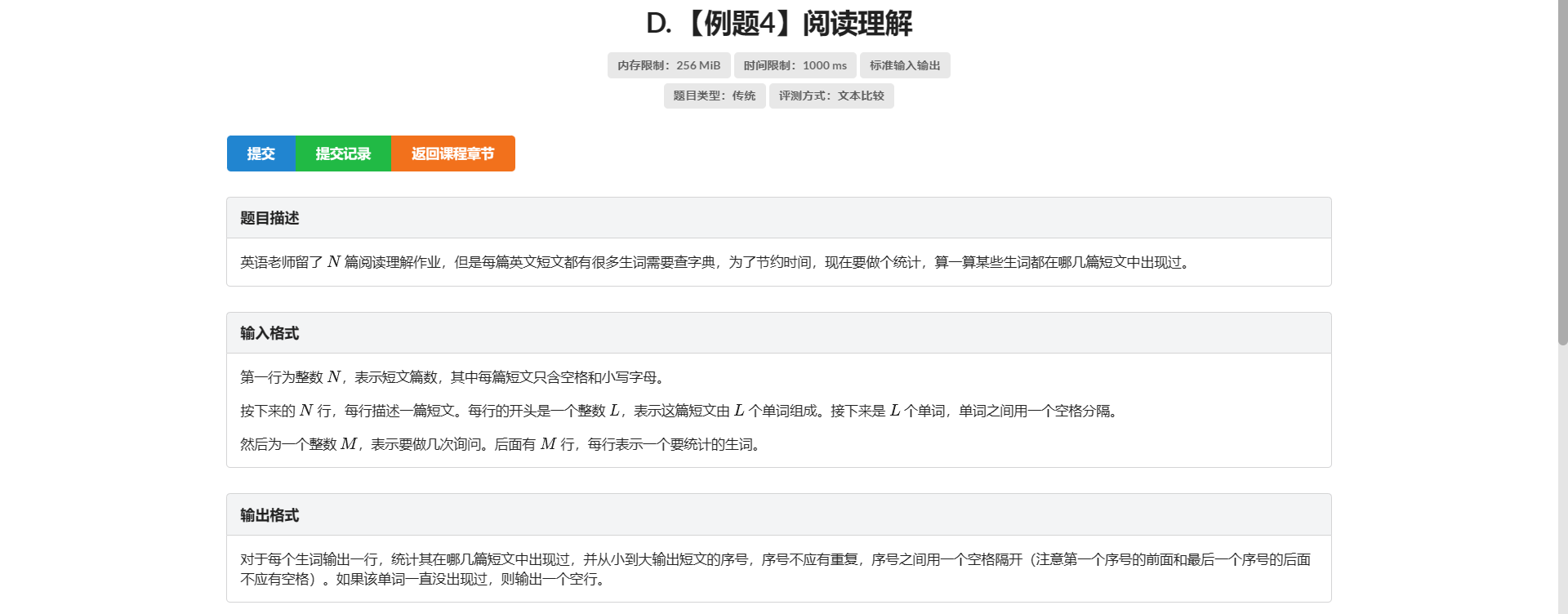
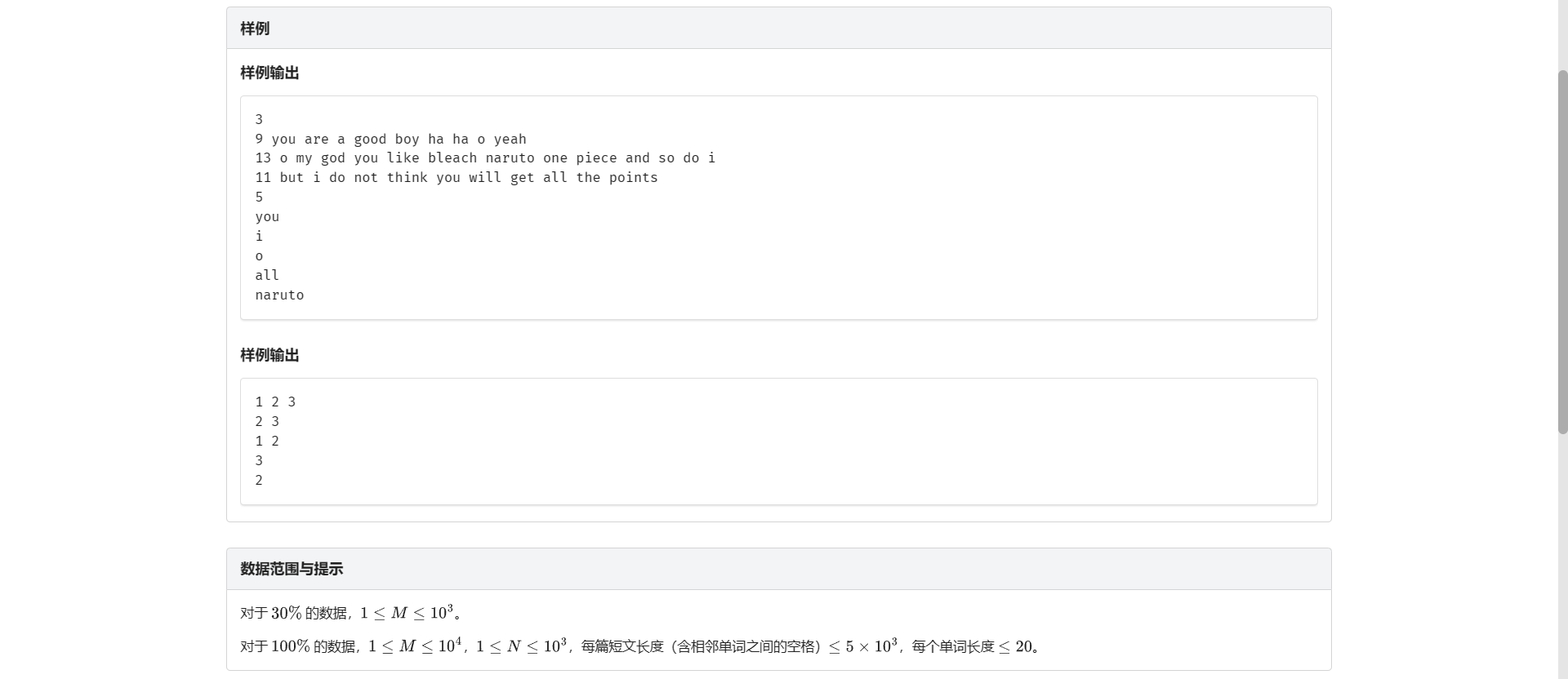
对于这题 我只能说 \(STL\) 大法好
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 0721;
bool vis[N];
map<string,vector<int> > m;
int main() {
int n;
scanf("%d",&n);
for (int i = 1; i <= n; ++i) {
int num;
scanf("%d",&num);
for (int j = 1; j <= num; ++j) {
string s;
cin >> s;
m[s].push_back(i);
}
}
int q;
scanf("%d",&q);
for (int i = 1; i <= q; ++i) {
memset(vis, 0, sizeof(vis));
string s;
cin >> s;
for (int j = 0; j < m[s].size(); ++j) {
if (!vis[m[s][j]]) {
printf("%d ",m[s][j]);
vis[m[s][j]] = 1;
}
}
printf("\n");
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号