YBTOJ 2.3KMP 算法

A.子串查找

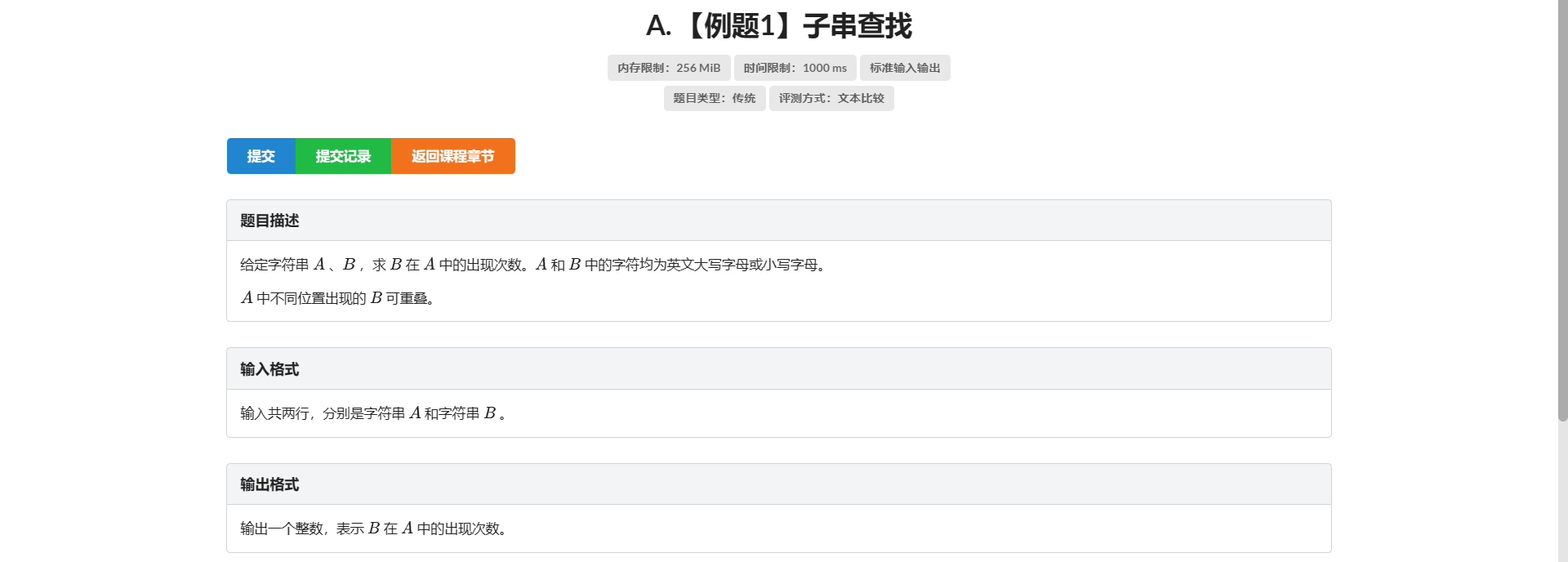
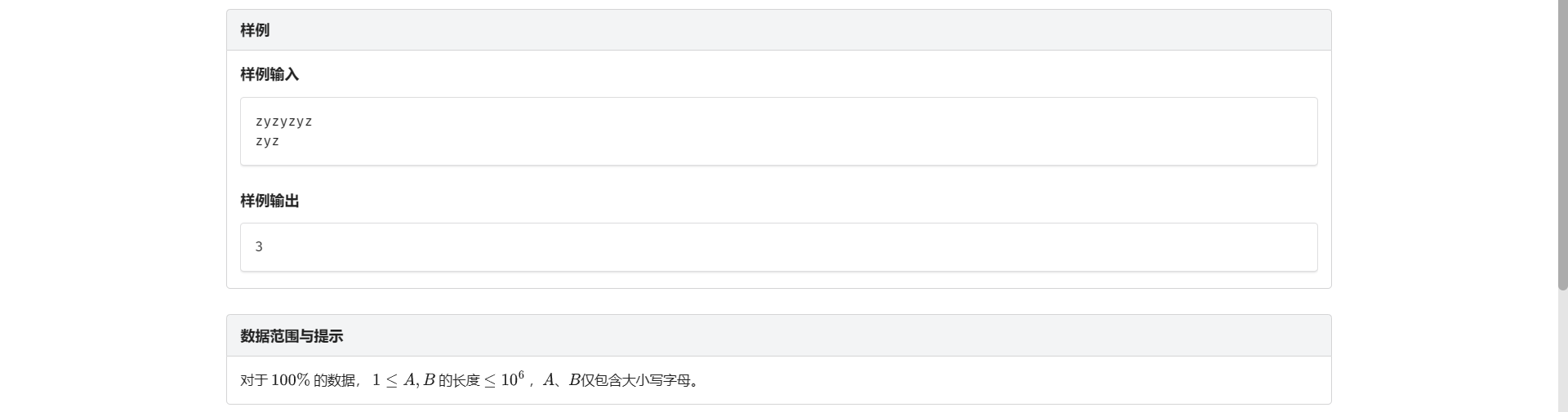
板子 详见KMP学习笔记

点击查看代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 0721;
char s1[N], s2[N];
int kmp[N];
int ans;

int main() {
    scanf("%s%s", s1, s2);
    int len1 = strlen(s1);
    int len2 = strlen(s2);
    for (int k = 0, i = 1; i < len2; ++i) {
        while (k && (s2[i] != s2[k])) k = kmp[k];
        if (s2[i] == s2[k])
            kmp[i + 1] = ++k;
        else
            kmp[i + 1] = 0;
    }
    for (int k = 0, i = 0; i < len1; ++i) {
        while (k && (s1[i] != s2[k])) k = kmp[k];
        if (s1[i] == s2[k])
            k++;
        else
            k = 0;
        if (k == len2)
            ++ans;
    }

    // for( int i = 1 ; i <= len2 ; ++i )
    // printf("%d " ,kmp[i] ) ;
    printf("%d", ans);

    return 0;
}

---

B.重复子串

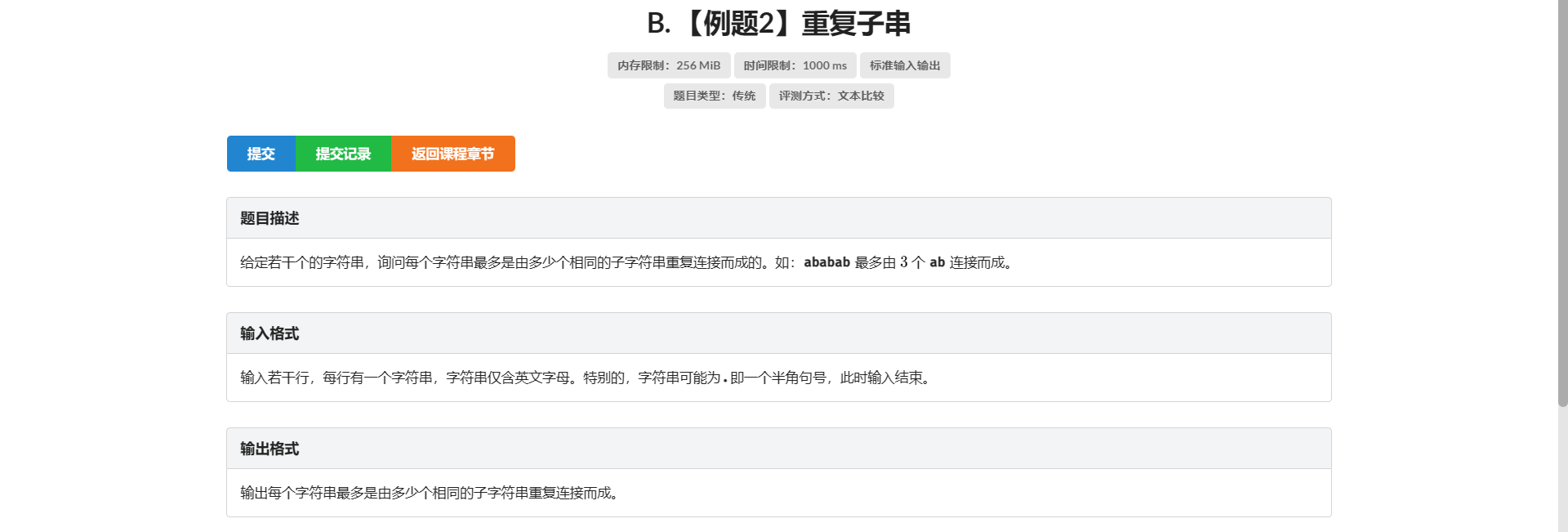
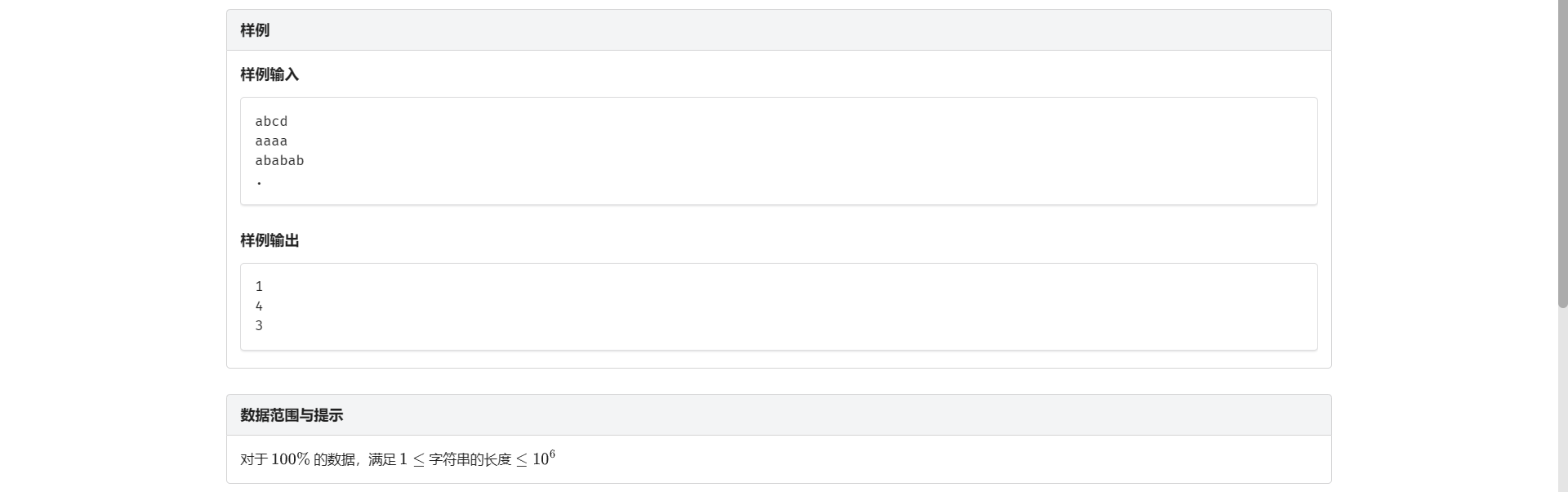
看到重复子串 想到最小循环节 进而想到 \(KMP\)
但是对于这题 如果最小循环节不是原串的约数 那么就代表它最后一次出现被砍掉了后面一段 显然是不符合题目条件的 这时候原串自己才是重复子串

点击查看代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 0721;
int nxt[N];

int main() {
	
	string s;
	while (cin >> s) {
		if (s[0] == '.')
			break;
		int len = s.length();
		memset(nxt, 0, sizeof(nxt));
		for (int i = 1, k = 0; i < len; ++i) {
			while (k && s[i] != s[k])
			k = nxt[k];
			
			if (s[i] == s[k])
			nxt[i+1] = ++k;
		
		}
		int cir = len - nxt[len];
		if (len % cir == 0)
			printf("%d\n",len / cir);
		else
			printf("1\n");		
	}
	
	return 0;
}

---

C.周期长度和

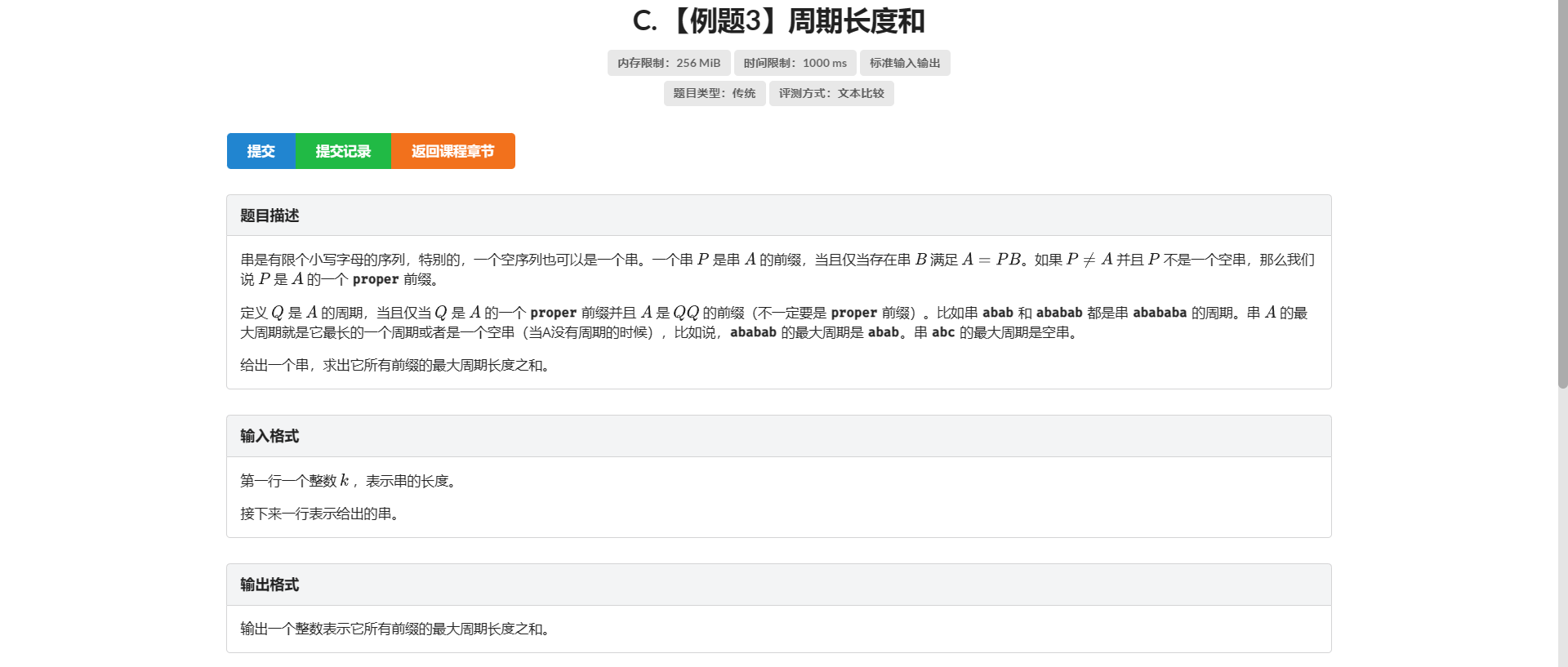
还是周期问题
并且是最大周期长度 也就是说最小 \(border\)
但是 \(10^6\) 的数据范围 暴力跳 \(fail\) 显然会寄掉
然后我们发现只需要跳到根节点的儿子节点 想到一个类似于路径压缩的东西

点击查看代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;

const int N = 1e6 + 0721;
int nxt[N];
char s[N];
int n;
ll ans;

int main() {
    scanf("%d", &n);
    scanf("%s", s);

    for (int i = 1, j = 0; i < n; ++i) {
        while (j && s[i] != s[j]) j = nxt[j];
        if (s[i] == s[j])
            nxt[i + 1] = ++j;
        else
            nxt[i + 1] = 0;
    }

    for (int i = 1; i <= n; ++i) {
        int j = i;
        while (nxt[j] != 0) j = nxt[j];
        if (nxt[i] != 0)
            nxt[i] = j;
        ans += i - j;
    }

    printf("%lld", ans);

    return 0;
}

---

D.子串拆分

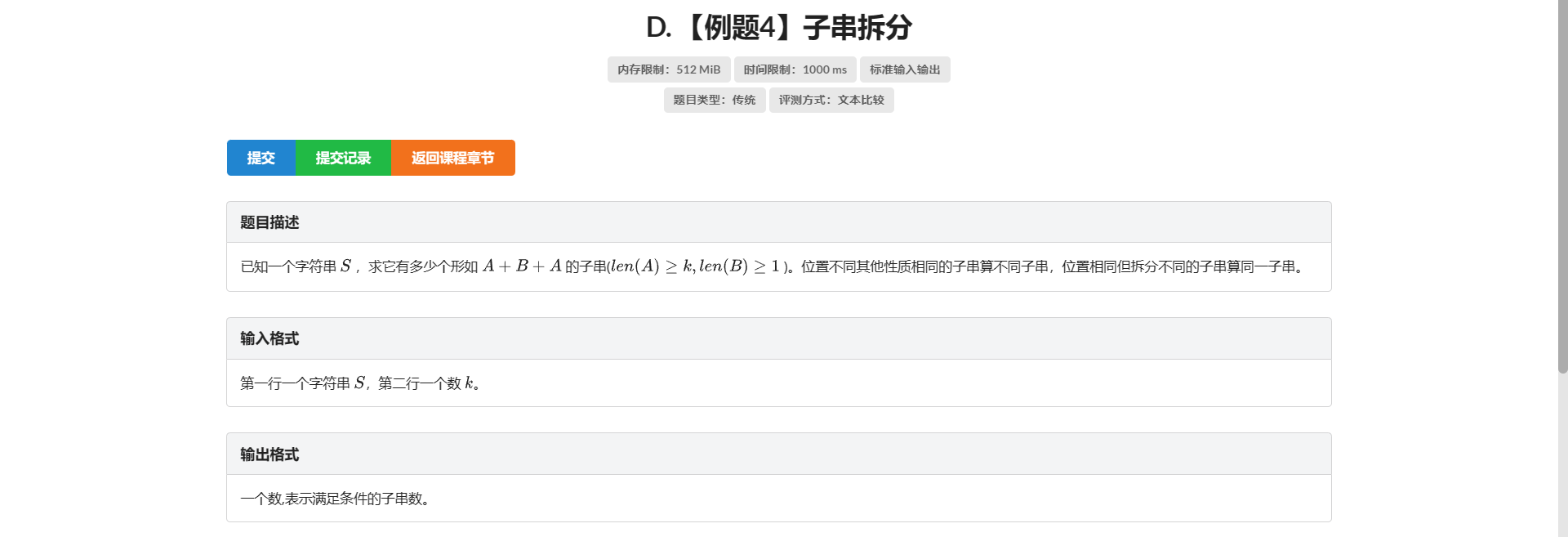
看到类似于 \(A + B + A\) 的形式 想到跳不重复 \(border\)
然后发现这题 \(O(n^2)\) 就能过 直接对每个子串暴力做 \(KMP\) 即可
代码咕了