YBTOJ 1.4深度搜索

A.拔河比赛

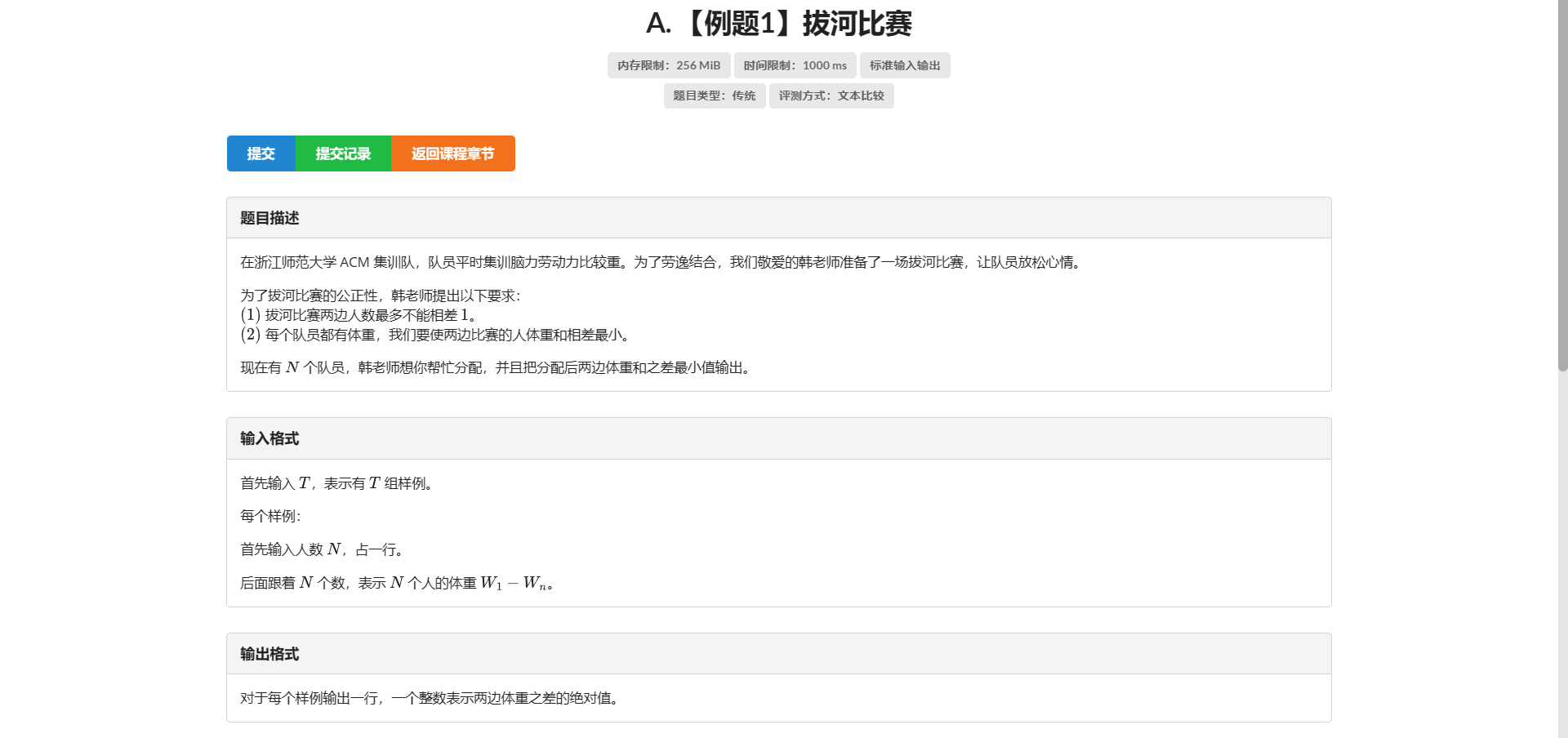
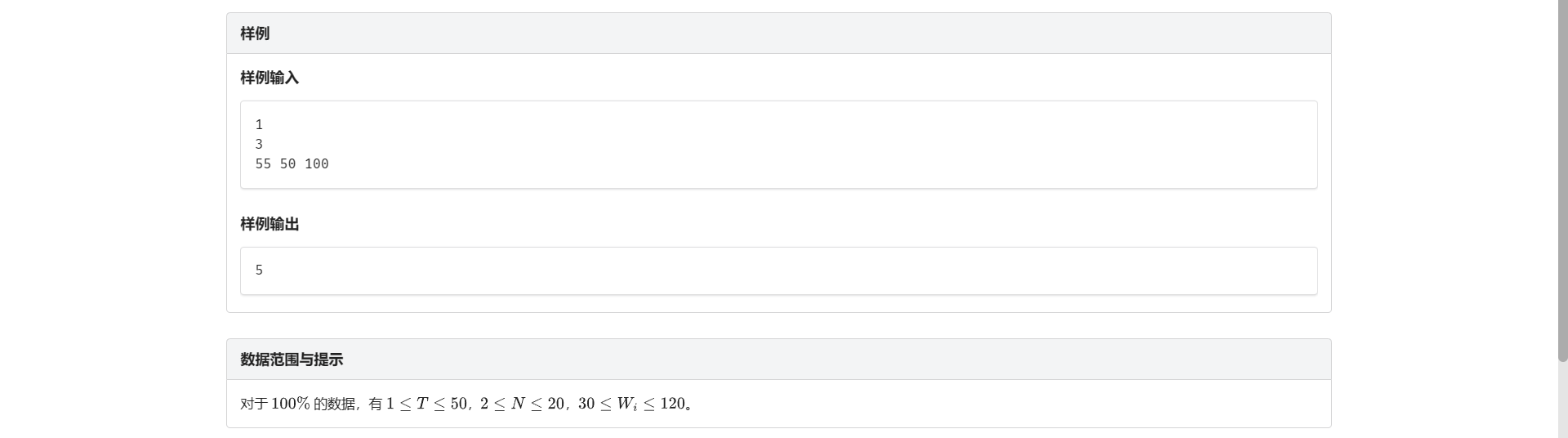
很经典的深搜
我们搜索把这个人放到/不放到这个队里的情况
然后当搜完更新答案即可

点击查看代码

#include <bits/stdc++.h>
using namespace std;

const int N = 0x0d00;
int w[N];
int t, n, half, minhalf;
float sum, ans;

void dfs(int x, float lef, int num) {
    if (lef <= 0 || x == n + 1 || num >= half) {
        if (num >= minhalf)
            ans = min(ans, fabs(lef));
        return;
    }

    dfs(x + 1, lef - w[x], num + 1);
    dfs(x + 1, lef, num);
}

int main() {
    scanf("%d", &t);
    while (t--) {
        scanf("%d", &n);
        memset(w, 0, sizeof(w));
        if (n % 2 == 0)
            half = n / 2, minhalf = half;
        else
            half = n / 2 + 1, minhalf = half - 1;

        sum = 0.0;
        for (int i = 1; i <= n; ++i) {
            scanf("%d", &w[i]);
            sum += (float)w[i];
        }
        sum /= 2;

        ans = 0x7fffffff;
        dfs(1, sum, 0);

        printf("%0.f\n", ans * 2);
    }

    return 0;
}

---

B.数独游戏

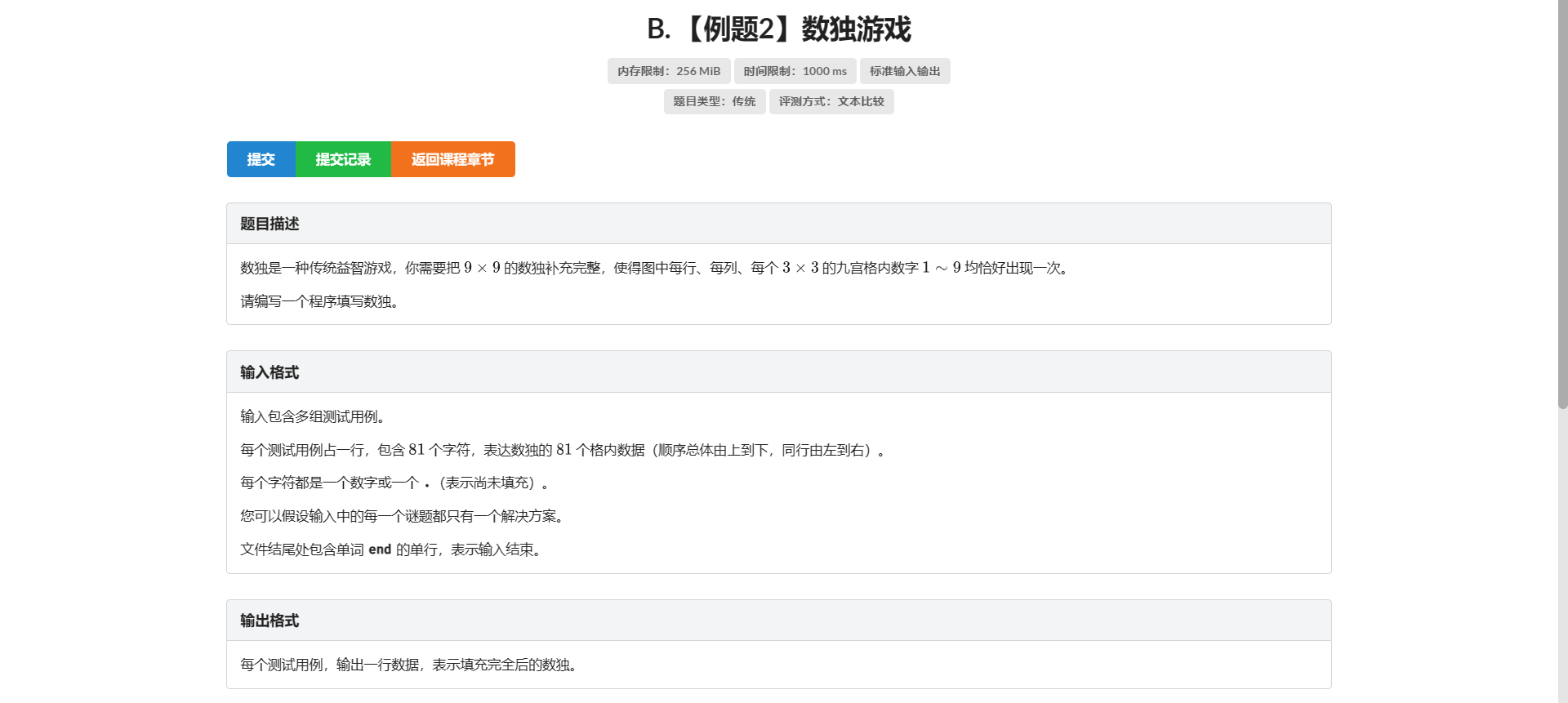
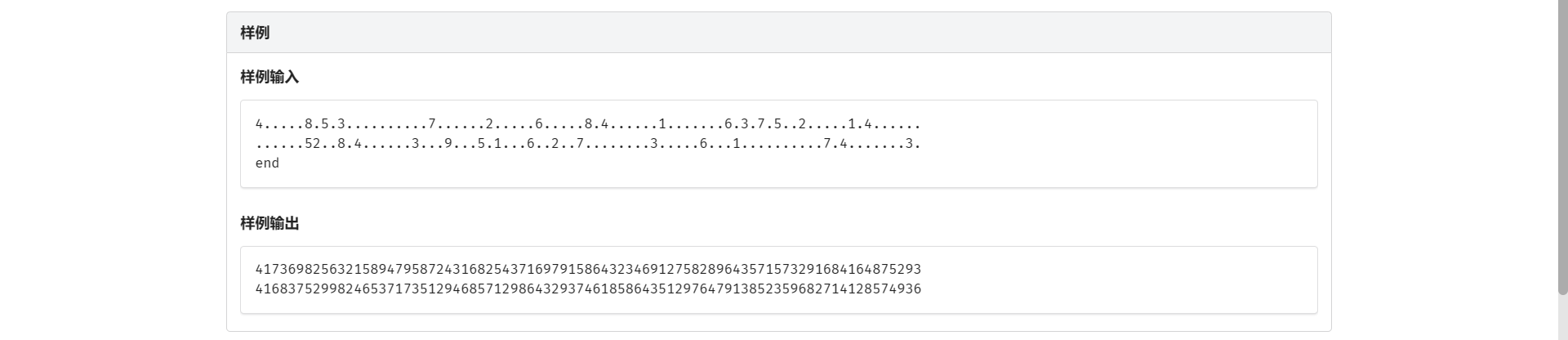
很好玩的一个东西
首先爆搜一眼T
我们考虑我们填数独游戏的过程 发现可以记录当前每个数在行列格的出现情况 然后进行剪枝

点击查看代码

#include <bits/stdc++.h>
using namespace std;

const int N = 10;
bool h[N][N], l[N][N], gg[N][N];
int a[N][N];
bool end;

inline int getgg(int x, int y) {
    if (y <= 3)
        return 1 + (x - 1) / 3;
    else if (y <= 6)
        return 4 + (x - 1) / 3;
    else
        return 7 + (x - 1) / 3;
}

void dfs(int x, int y) {
    if (end)
        return;

    if (x == 10)
        x = 1, ++y;

    if (x == 1 && y == 10) {
        for (int i = 1; i <= 9; ++i) {
            for (int j = 1; j <= 9; ++j) printf("%d", a[i][j]);
        }
        printf("\n");
        end = 1;
        return;
    }

    if (end)
        return;

    if (a[x][y] != 0)
        dfs(x + 1, y);
    else {
        for (int i = 1; i <= 9; ++i) {
            //			cout<<x<<" "<<y<<" "<<getgg(x,y)<<endl;
            if (!h[x][i] && !l[y][i] && !gg[getgg(x, y)][i]) {
                a[x][y] = i;
                h[x][i] = 1;
                l[y][i] = 1;
                gg[getgg(x, y)][i] = 1;

                dfs(x + 1, y);

                a[x][y] = 0;
                h[x][i] = 0;
                l[y][i] = 0;
                gg[getgg(x, y)][i] = 0;
            }
        }
    }
    return;
}

int main() {
    string s;
    while (cin >> s) {
        if (s[0] == 'e')
            break;

        memset(h, 0, sizeof(h));
        memset(l, 0, sizeof(l));
        memset(gg, 0, sizeof(gg));
        memset(a, 0, sizeof(a));

        for (int i = 0; i < 81; ++i) {
            int y = (i + 1) % 9;
            int x = (i + 1) / 9 + 1;
            if (y == 0)
                y = 9, --x;
            //			cout<<endl<<x<<" "<<y<<endl;
            if (s[i] != '.') {
                int num = s[i] - '0';
                a[x][y] = num;
                h[x][num] = 1;
                l[y][num] = 1;
                gg[getgg(x, y)][num] = 1;
            }
        }

        end = 0;
        dfs(1, 1);
    }

    return 0;
}

---

C.虫食算

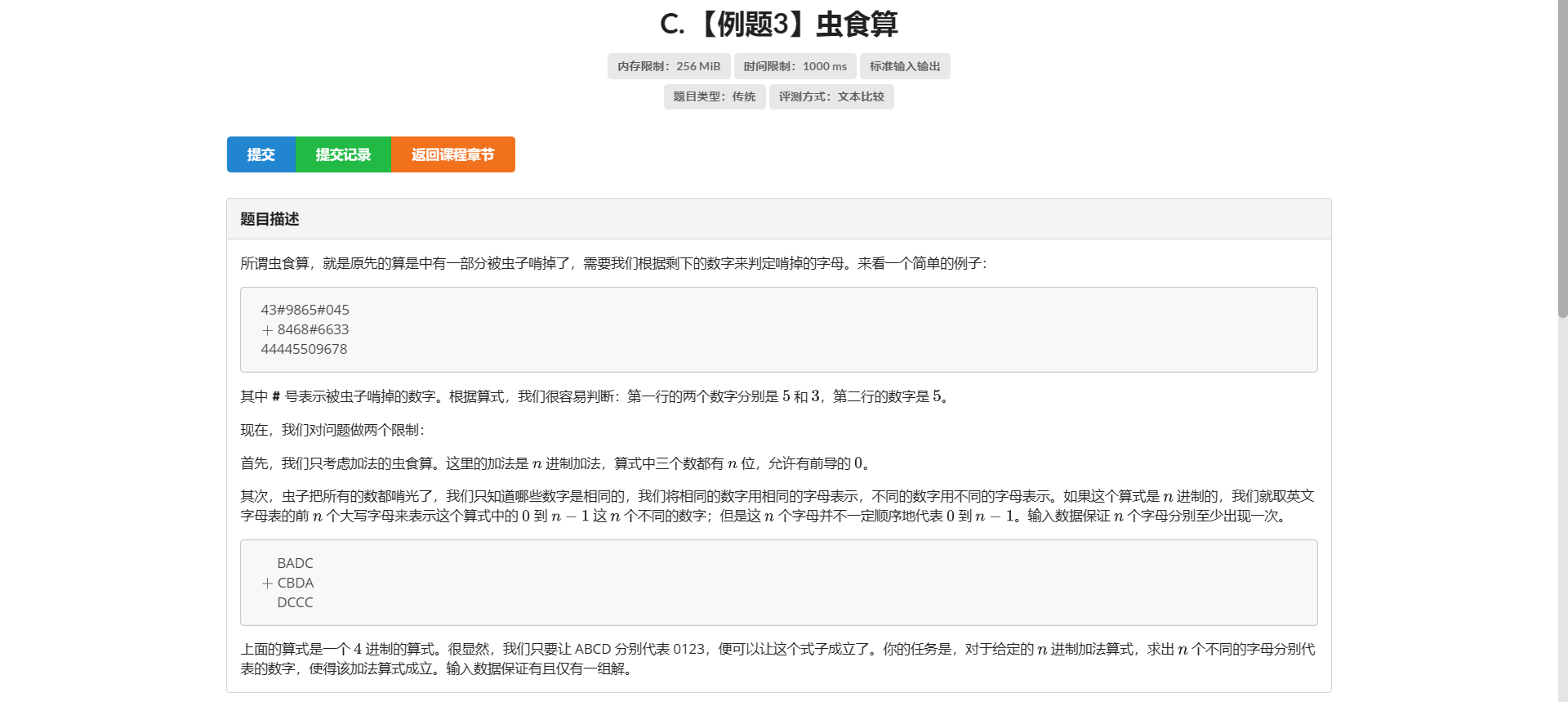
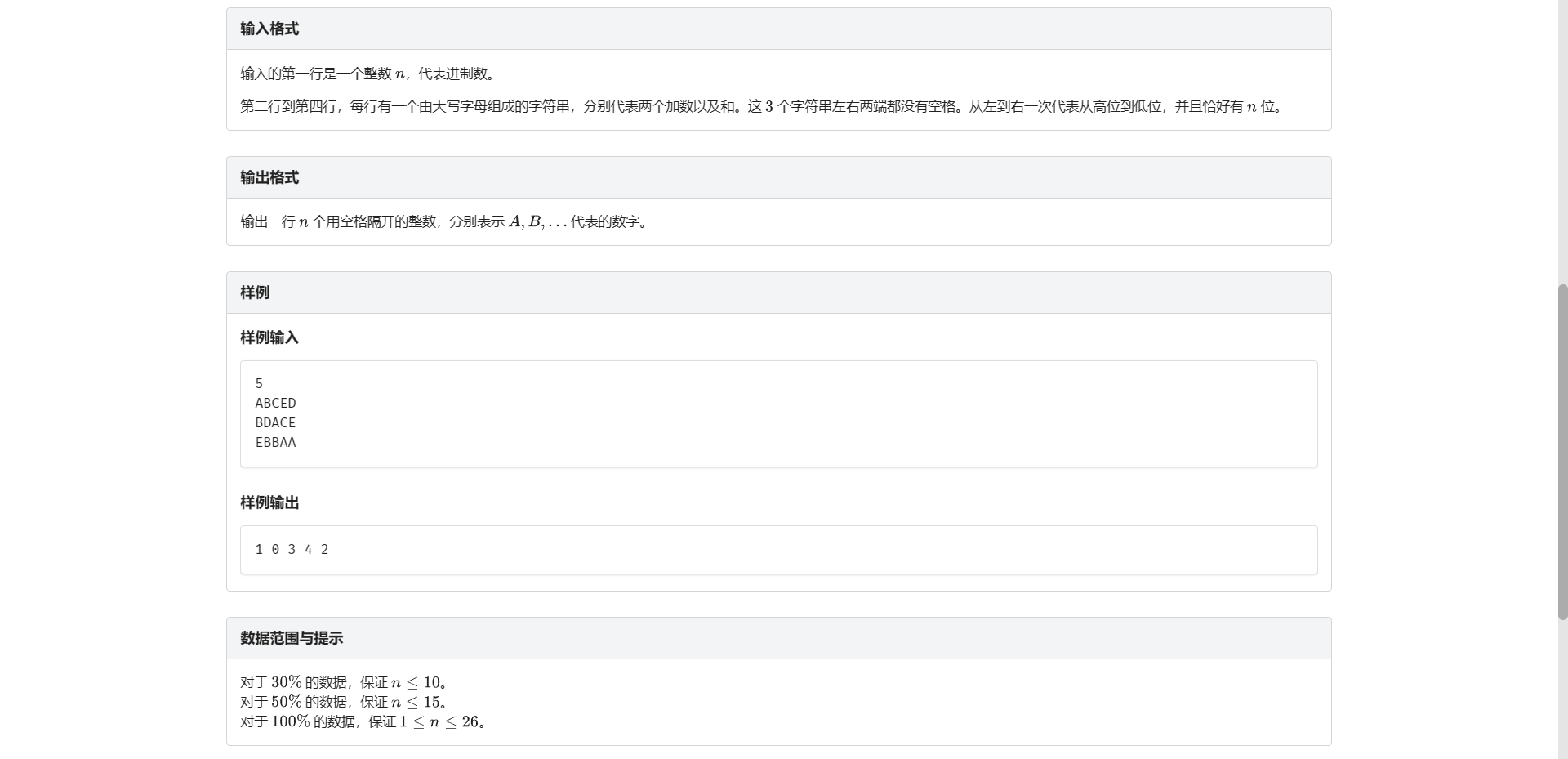
非常的谔谔啊
因为要进位 所以要从低位向高位搜

点击查看代码

#include <bits/stdc++.h>
using namespace std;

string s[4];
bool vis[26];
int n, len;
map<char, int> m;

void dfs(int x, int y, int t) {
    //	cout << x << " " << y << " " << t << endl;
    //	for (int i = 'A'; i <= 'A' + n - 1; ++i)
    //	printf("%d ",m[i]);
    //	cout<<endl;

    if (x == -1) {
        if (t != 0)
            return;
        else {
            for (int i = 'A'; i <= 'A' + n - 1; ++i) printf("%d ", m[i]);
            exit(0);
        }
    }

    if (y == 1) {
        if (m[s[y][x]] != -1)
            dfs(x, y + 1, t);
        else {
            for (int i = n - 1; i >= 0; --i) {
                if (!vis[i]) {
                    if (m[s[3][x]] != -1 && m[s[2][x]] != -1 && (m[s[2][x]] + i + t) % n != m[s[3][x]])
                        continue;

                    m[s[y][x]] = i;
                    vis[i] = 1;

                    dfs(x, y + 1, t);

                    m[s[y][x]] = -1;
                    vis[i] = 0;
                }
            }
        }
    } else if (y == 2) {
        if (m[s[y][x]] != -1)
            dfs(x, y + 1, t);
        else {
            for (int i = n - 1; i >= 0; --i) {
                if (!vis[i]) {
                    if (m[s[3][x]] != -1 && (m[s[1][x]] + i + t) % n != m[s[3][x]])
                        continue;

                    m[s[y][x]] = i;
                    vis[i] = 1;

                    dfs(x, y + 1, t);

                    m[s[y][x]] = -1;
                    vis[i] = 0;
                }
            }
        }
    } else {
        if (m[s[y][x]] != -1) {
            if ((m[s[1][x]] + m[s[2][x]] + t) % n == m[s[3][x]])
                dfs(x - 1, 1, (m[s[1][x]] + m[s[2][x]] + t) / n);
            else
                return;
        } else {
            for (int i = n - 1; i >= 0; --i) {
                //				cout<<i<<" "<<(m[s[1][x]] + m[s[2][x]] + t) % n<<endl;
                if (!vis[i] && (m[s[1][x]] + m[s[2][x]] + t) % n == i) {
                    m[s[y][x]] = i;
                    vis[i] = 1;

                    dfs(x - 1, 1, (m[s[1][x]] + m[s[2][x]] + t) / n);

                    m[s[y][x]] = -1;
                    vis[i] = 0;
                }
                //				else
                //				return;
            }
        }
    }
}

int main() {
    //	freopen("P1092_9.in", "r", stdin);

    scanf("%d", &n);
    cin >> s[1] >> s[2] >> s[3];
    len = s[1].length();

    for (int i = 'A'; i <= 'Z'; ++i) m[i] = -1;

    if (n == 20) {
        printf("18 14 0 9 15 17 7 13 12 16 1 10 4 2 8 5 11 3 6 19");
        return 0;
    } else
        dfs(len - 1, 1, 0);

    return 0;
}

---

D.生日蛋糕

那天看到一个说法 感觉确实挺有道理的

搜索题适合找个心情悠闲的时候写

考虑枚举每层的半径和高

具体搜索过程就不讲了 这里说几个剪枝

• 上下界剪枝：考虑每层能枚举的半径和高的范围 因为每层的半径和高都是严格递减的 所以假如铺完这层上面还有 \(x\) 层 那么这层最小的高和半径就到 \(x + 1\) 了

• 最优性剪枝：如果上面每一层的高和半径都取到最小 得到的答案还是比当前答案大 直接返回

• 可行性剪枝：如果上面每一层的高和半径都取到最大 得到的体积还是不足 \(N\) 直接返回

点击查看代码

#include <bits/stdc++.h>
using namespace std;

namespace steven24 {

int N, M;
int ans = 0x7fffffff;

void dfs(int ceng, int lstr, int lsth, int nowans, int leftv) {
	if (nowans > ans) return; //最优性剪枝
	if (ceng == M + 1) {
		if (leftv) return; //如果还有剩的体积
		ans = min(nowans, ans); //不取min直接赋值因为之前的最优性剪枝似乎也行（？
		return; 
	} 
	int left = M - ceng + 1; //上面还能铺多少层
	if (left * lstr * lstr * lsth <= leftv) return; //如果上面全取最大值还是不够体积
	if ((left << 1) + nowans > ans) return; //如果上面left层都取最小的半径和高
	for (int r = lstr - 1; r >= left; --r) {
		for (int h = lsth - 1; h >= left; --h) {
			int v = r * r * h; //这层的体积 
			int s = 2 * r * h; //这层的侧面积
			if (leftv < v) continue;
			if (nowans + s > ans) continue;
			
			if (ceng == 1) dfs(ceng + 1, r, h, nowans + s + r * r, leftv - v); //在最底层要加上底面积
			else dfs(ceng + 1, r, h, nowans + s, leftv - v);
		}
	} 
	
}

void main() {
	scanf("%d%d", &N, &M);
	dfs(1, 50, 50, 0, N);
	printf("%d\n", ans);
}

}

int main() {
	steven24::main();
	return 0;
}
/*
100
2
*/

---

E.最大费用

看到 \(n \le 40\) 还以为是什么神秘剪枝 遂写了一发 TLE50pts

看题解才知道是双向搜索
首先 dfs 出前一半物品可能获得的花费
然后 dfs 出后一半物品可能获得的花费

这样我们枚举其中一半可能获得的花费 然后二分查找另一半即可

写的时候没想好用 lower_bound 还是 upper_bound 遂挂之

点击查看代码

#include <bits/stdc++.h>
using namespace std;

namespace steven24 {

const int N = 5e6 + 0721;
int a[N], ans;
int q[N], h[N], top1, top2;
int n, m;

void dfs1(int id, int left) {
	if (id == n / 2 + 1) {
		h[++top1] = m - left;
		return;
	}
	dfs1(id + 1, left);
	if (left - a[id] < 0) { //小优化 因为我们按价值排序 这个选不了后面所有的都选不了 直接返回 
		h[++top1] = m - left;
		return;
	} else
		dfs1(id + 1, left - a[id]);
}

void dfs2(int id, int left) {
	if (id == n + 1) {
		q[++top2] = m - left;
		return;
	}
	dfs2(id + 1, left);
	if (left - a[id] < 0) {
		q[++top2] = m - left;
		return;
	} else 
		dfs2(id + 1, left - a[id]);
}

void main() {
	
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
	sort(a + 1, a + 1 + n);
	dfs1(1, m);
	dfs2(n / 2 + 1, m);
	
	sort(h + 1, h + 1 + top1);
	sort(q + 1, q + 1 + top2);
	
	for (int i = 1; i <= top1; ++i) {
		int loc = upper_bound(q + 1, q + 1 + top2, m - h[i]) - q - 1;
		if (loc) ans = max(ans, h[i] + q[loc]);
	}
	
	printf("%d", ans);
}

}

int main() {
	steven24::main();
	return 0;
}
/*
4 10
4 3 5 11
*/