YBTOJ 1.3二分算法
A.数列分段
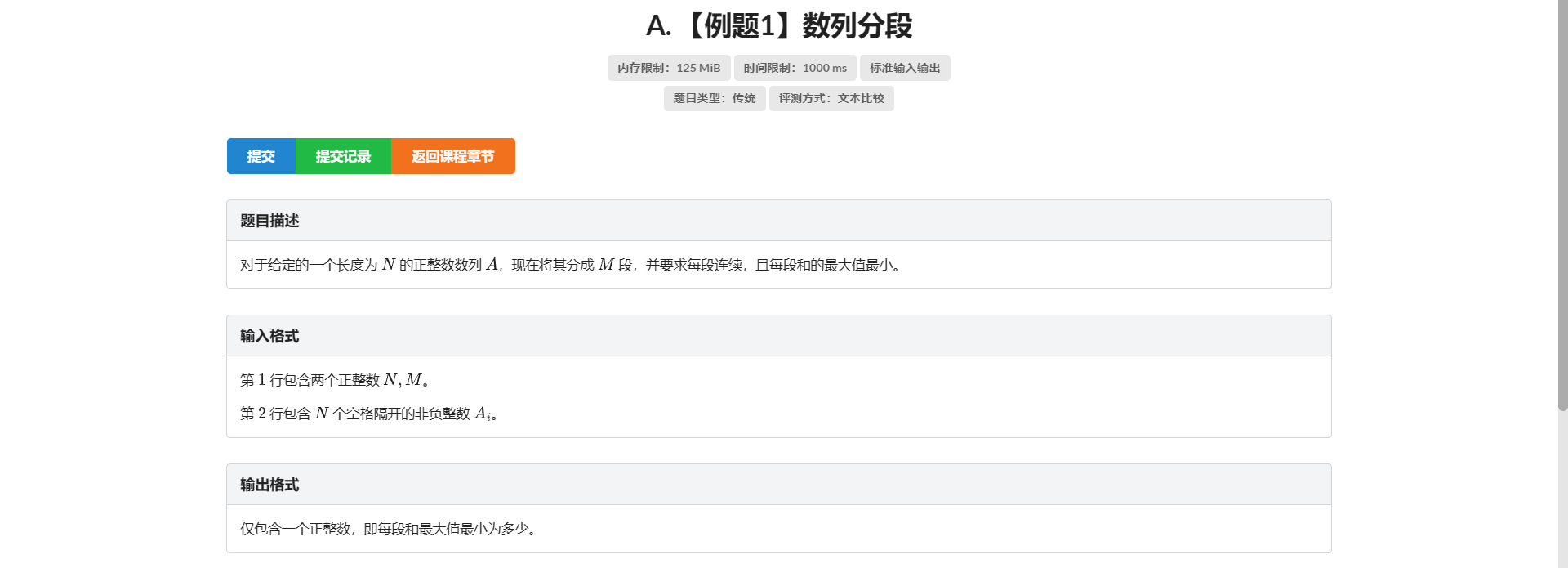
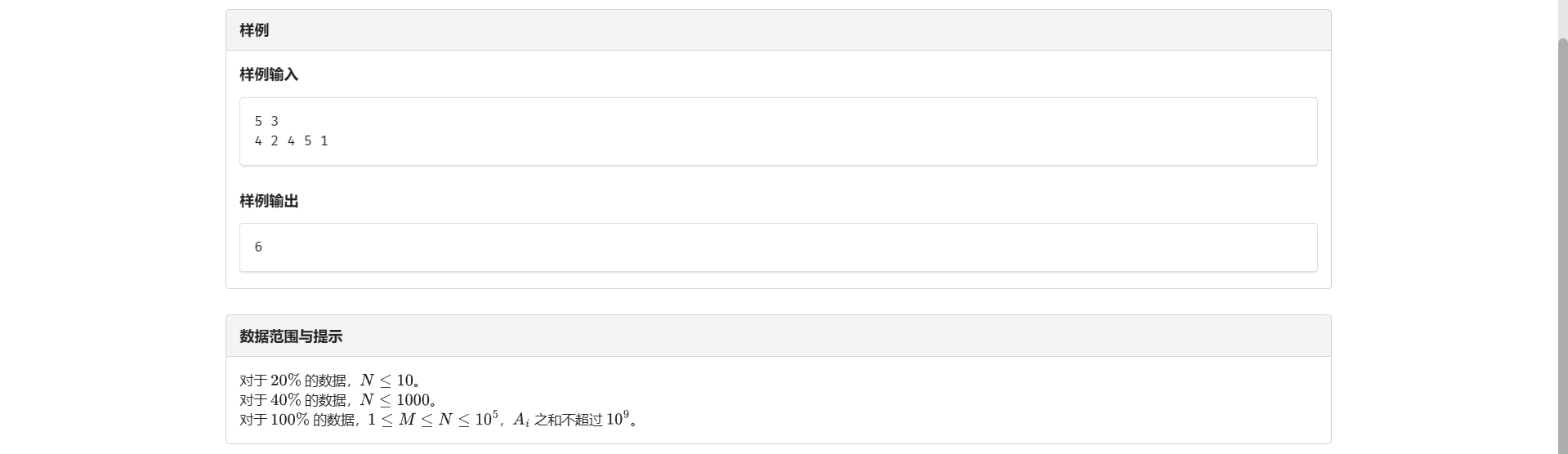
最大值最小 想到二分答案
并且答案具有单调性 经典二分
我们对于二分的答案 把数列从左往右扫 当前和加上下一个数就大于答案 那么就分段
统计段数小于等于 \(M\) 就行(因为要求是和的最大值所以不够的可以把分好的区间再分几段)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 0721;
int a[N];
int n, k, sum, maxa;
bool check(int x) {
int tot = 1;
int nowsum = 0;
for (int i = 1; i <= n; ++i) {
if (nowsum + a[i] > x) {
++tot;
nowsum = a[i];
} else
nowsum += a[i];
}
// cout<<x<<" "<<tot<<endl;
return tot <= k;
}
int find(int l, int r) {
int mid, ans;
while (l <= r) {
mid = l + (r - l >> 1);
if (check(mid)) {
ans = mid;
r = mid - 1;
// cout<<"ans="<<ans<<endl;
} else
l = mid + 1;
// cout<<"1";
}
// cout<<"return's ans="<<ans<<endl;
return ans;
}
int main() {
scanf("%d%d", &n, &k);
maxa = -0x7fffffff;
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]), sum += a[i], maxa = max(maxa, a[i]);
// cout<<maxa<<" "<<sum<<endl ;
printf("%d", find(maxa, sum));
return 0;
}
B.防具布置
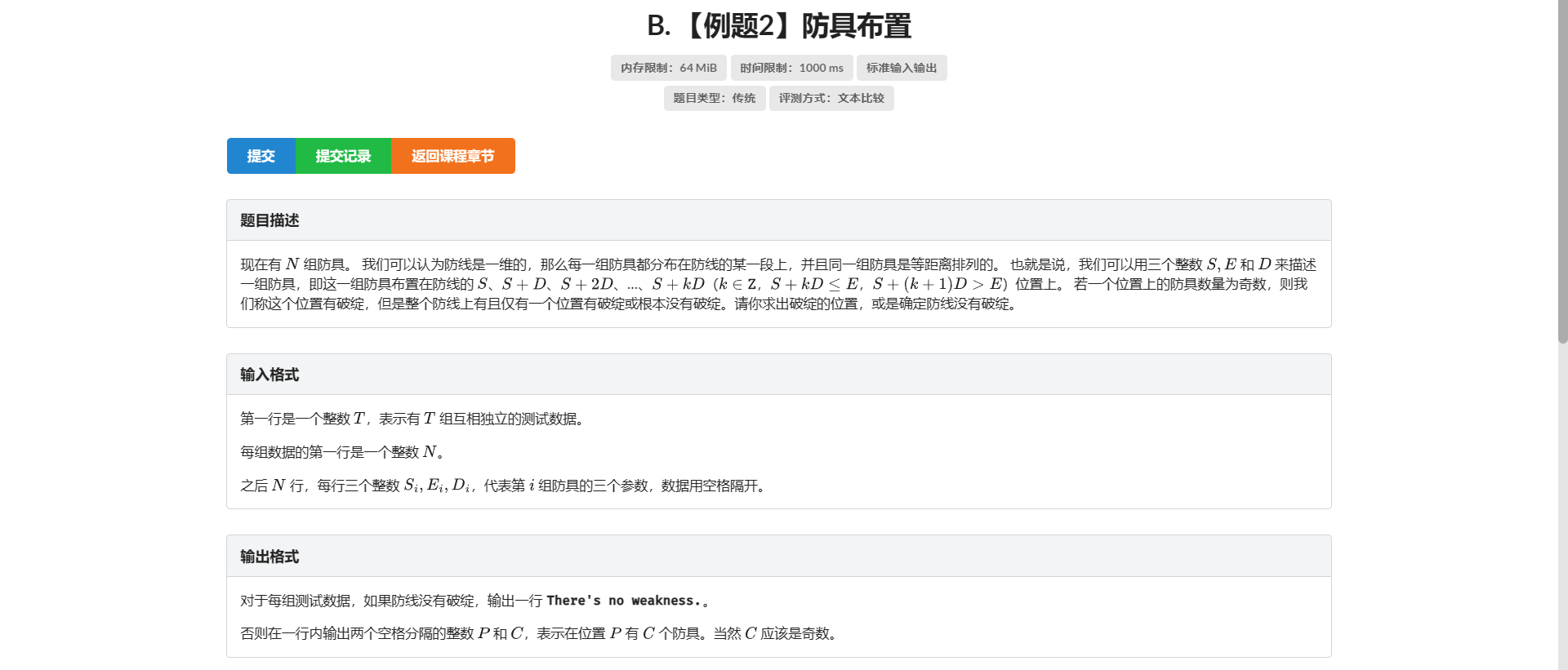
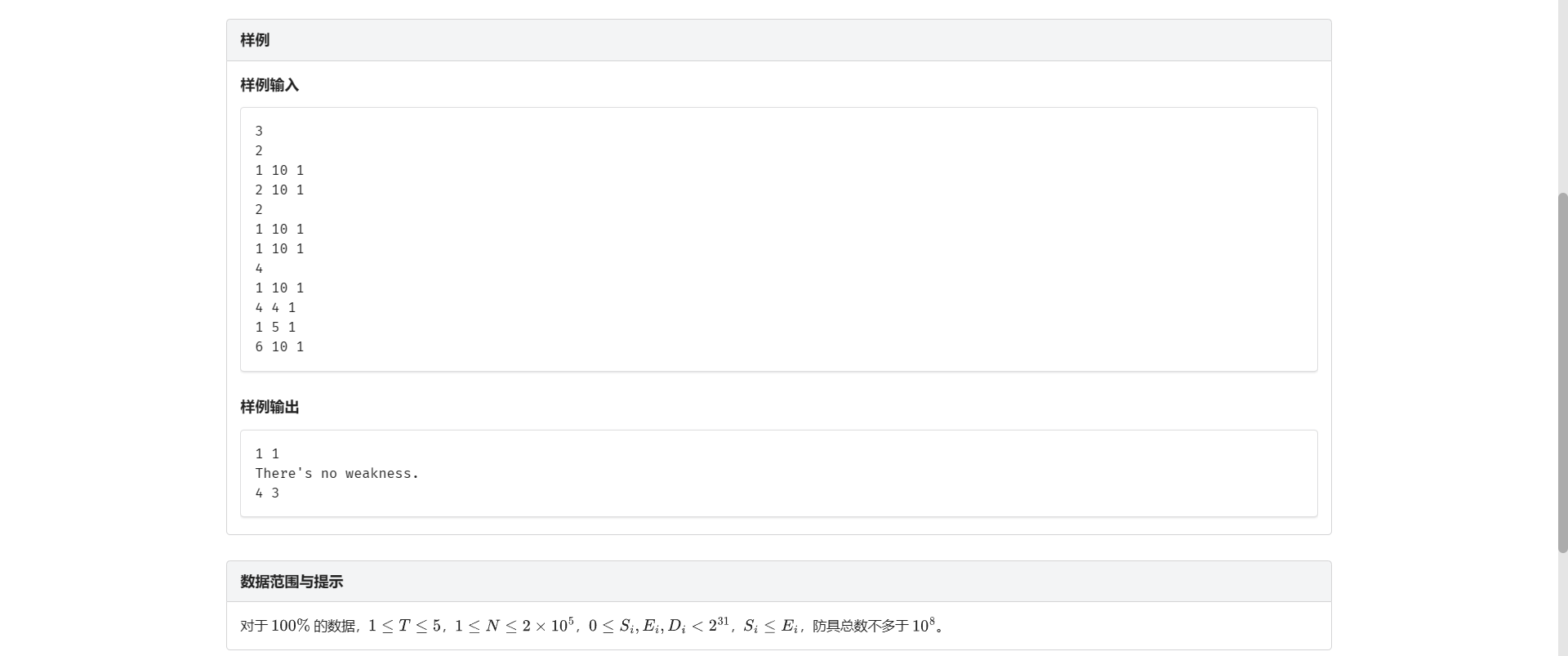
首先这题暴力统计 \(2^{31}\) 的数据会T飞
我们找这题的特殊性质
观察到题目有一句“整个防线上有且仅有一个位置有破绽或根本没有破绽”
这代表着整个防线只有一个奇数或者一个奇数都没有
我们想想为什么要强调只有一个奇数 只有一个奇数和全是偶数有什么区别
然后就会发现如果求前缀和的话 如果有奇数的话就会以那个奇数为分界 前面前缀和都是偶数 后面的前缀和都是奇数
然后就可以二分找到这个点
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5 + 0721;
int s[N], e[N], d[N];
int T, n;
ll cnt(int x) {
ll tot = 0;
for (int i = 1; i <= n; ++i) {
if (s[i] <= x) {
if (e[i] <= x)
tot += (e[i] - s[i]) / d[i] + 1;
else
tot += (x - s[i]) / d[i] + 1;
}
}
return tot;
}
int find(int l, int r) {
int ans, mid;
while (l <= r) {
mid = l + (r - l >> 1);
// cout << l << " " << r << " " << mid << endl;
if (cnt(mid) % 2 == 1) {
ans = mid;
r = mid - 1;
} else
l = mid + 1;
// cout<<ans<<endl;
}
// cout<<ans<<endl;
return ans;
}
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d%d%d", &s[i], &e[i], &d[i]);
int last = (1 << 31) - 1;
if (cnt(last) % 2 == 0) {
printf("There's no weakness.\n");
continue;
}
int ans = find(1, last);
// cout<<last<<endl;
printf("%d %lld\n", ans, cnt(ans) - cnt(ans - 1));
}
return 0;
}
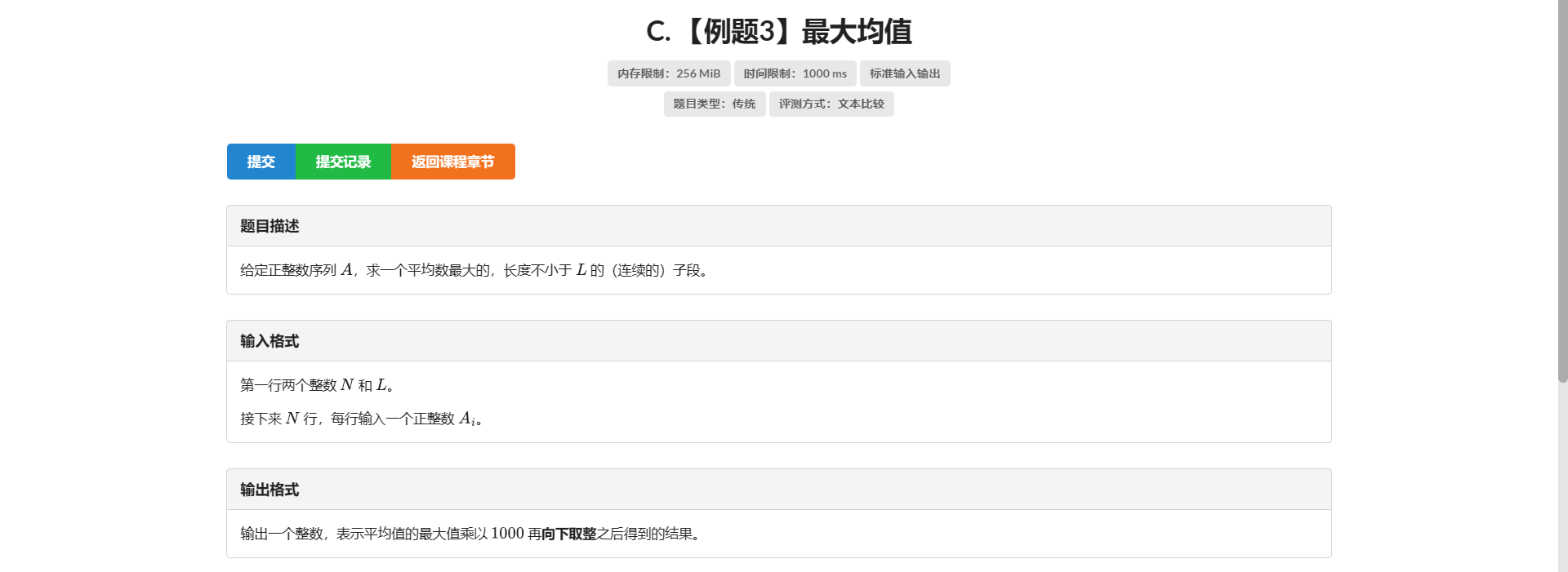
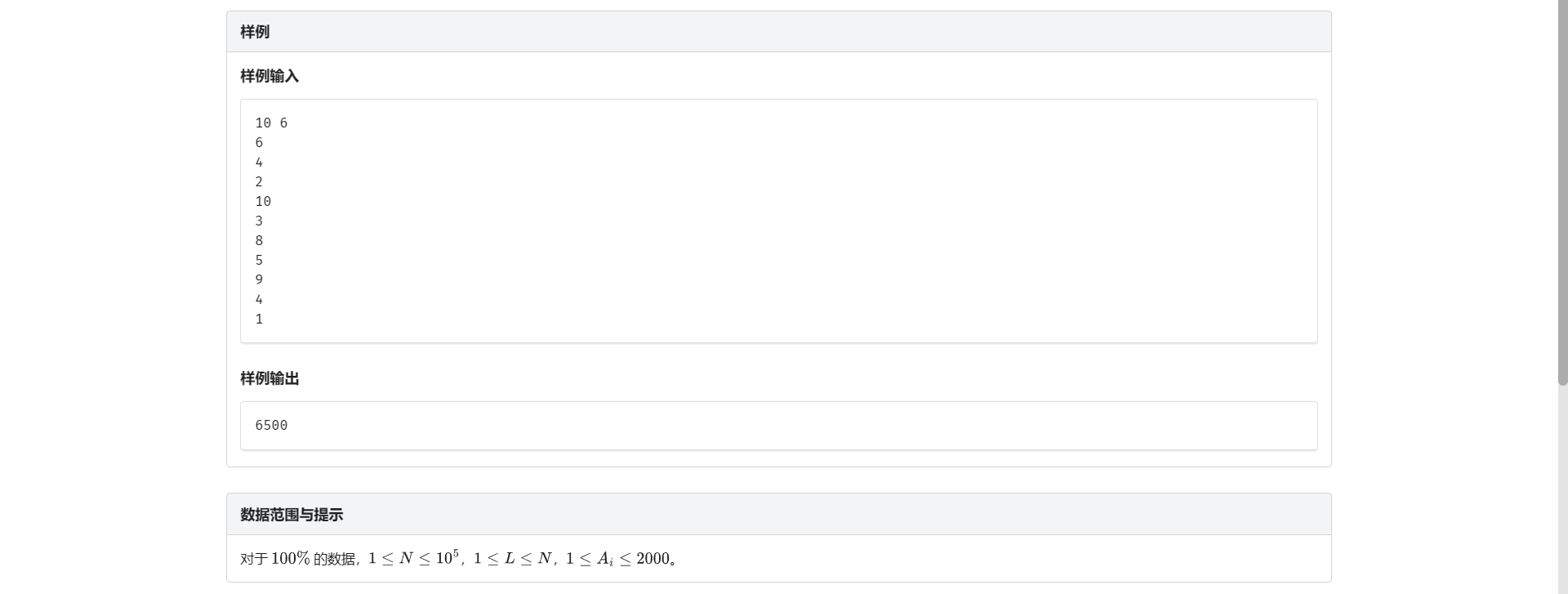
C.最大均值
一上来想的是双指针去做这个东西 结果发现这个区间的均值不具有单调性
然后就不会做了
实际上可以二分答案 判断是否存在一段长度不小于 \(L\) 的区间满足平均值大于等于 \(mid\)
我们把每个数都减去 \(mid\) 判断是否有区间和为非负数
可以将区间和转化为前缀和的差
那么我们就需要维护对于每个位置 \(i\) 在它前面隔了 \(L\) 个单位的前面那段区间的最小前缀和 用 \(a[i] - minn[i]\) 即可
点击查看代码
#include <bits/stdc++.h>
#define db double
using namespace std;
const int N = 2e5 + 0721;
int a[N];
db b[N], f[N], mina[N];
int n, L;
bool check(db x) {
for (int i = 1; i <= n; ++i) b[i] = a[i] - x;
for (int i = 1; i <= n; ++i) f[i] = b[i] + f[i - 1];
if (f[L] > 0)
return 1;
for (int i = L + 1; i <= n; ++i) {
mina[i] = min(mina[i - 1], f[i - L]);
if (f[i] - mina[i] >= 0)
return 1;
}
return 0;
}
int find(db l, db r) {
db mid;
while (r - l > 1e-5) {
mid = l + (r - l) / 2;
if (check(mid))
l = mid;
else
r = mid;
}
return floor(r * 1000);
}
int main() {
scanf("%d%d", &n, &L);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
}
printf("%d", find(0.0, 2000.0));
return 0;
}
F.攻击法坛
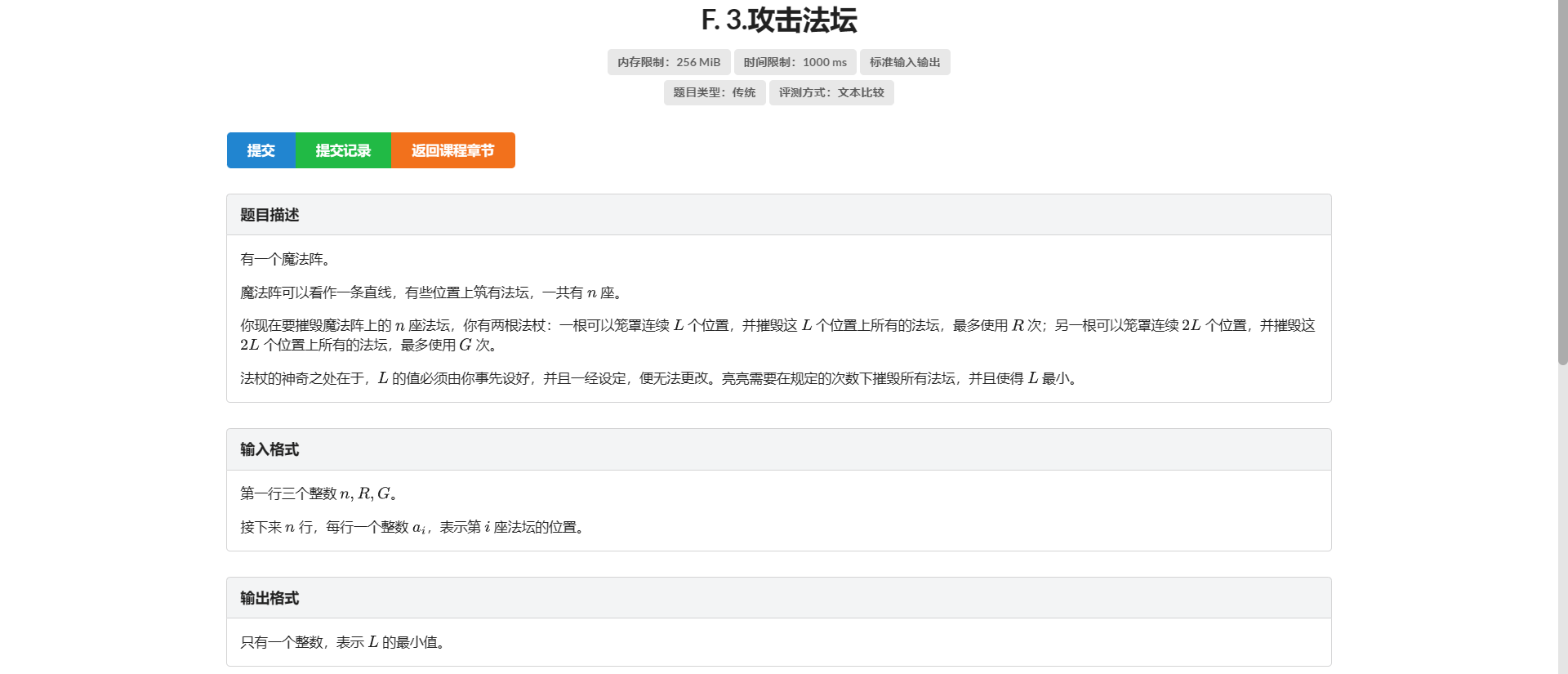
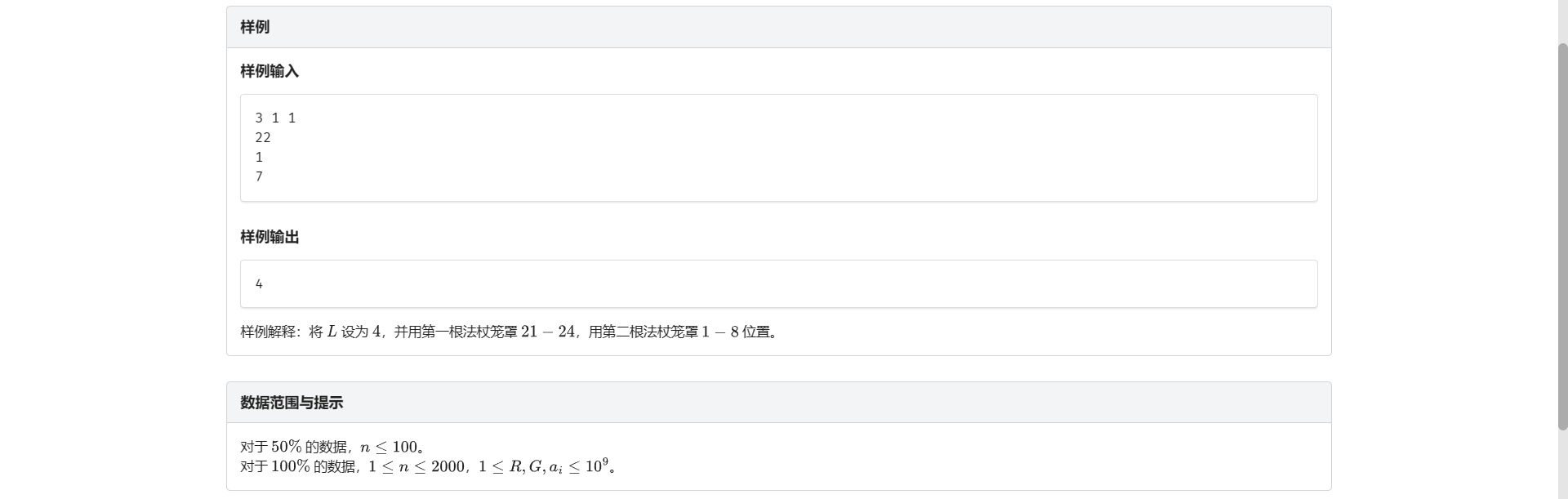
首先答案非常具有单调性 考虑二分答案
然后发现这题的数据范围可以支持我们用 \(\text O (n^2)\) 的复杂度来 check
那么我们考虑直接设 \(f_{i, j}\) 表示用了 \(i\) 次 1 法杖 用了 \(j\) 次 2 法杖能到达的最远点
很显然的 我们要先把点排序
然后考虑转移 以使用 1 法杖为例 有 \(f_{i + 1, j} = \max {(f_{i + 1, j}, nxt_{f_{i, j + 1}})}\)
其中 \(nxt_i\) 表示把一根 1 法杖一端覆盖在第 \(i\) 个点 另一端能覆盖到的最远点
进而想到直接预处理出对于每个点 表示把一根 1 / 2 法杖一端覆盖在该点 另一端能覆盖到的最远点
然后我们注意到这个东西似乎是 \(\text O (W \times G)\) 的
但是我们发现当 \(W + G \ge n\) 时 答案必定为 \(1\)
所以 \(f\) 数组的两维都开到 \(2000\) 即可
点击查看代码
#include <bits/stdc++.h>
using namespace std;
namespace steven24 {
const int N = 0x0d00;
int g[N][N], nxt[N][2];
int w[N];
int n, R, G;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
bool check(int x) {
memset(g, 0, sizeof g);
for (int i = 1; i <= n; ++i) {
for (int j = i; j <= n; ++j) {
if (w[j] - w[i] + 1 <= x) {
nxt[i][0] = j;
}
if (w[j] - w[i] + 1 <= (x << 1)) {
nxt[i][1] = j;
} else
break;
}
}
nxt[n + 1][0] = nxt[n + 1][1] = n; //小优化 如果在f[W][G]之前已经到了第n个点 那么转移的时候就会跳到第 n + 1 个点 我们直接让它跳回到 n 就能保证后面的答案都是 n
g[0][0] = 0;
for (int i = 0; i <= R; ++i) {
for (int j = 0; j <= G; ++j) {
int lst = g[i][j] + 1;
g[i + 1][j] = max(g[i + 1][j], nxt[lst][0]);
g[i][j + 1] = max(g[i][j + 1], nxt[lst][1]);
}
}
return g[R][G] == n;
}
int binary_search() {
int l = 0, r = 1e9;
int mid, ans;
while (l <= r) {
mid = ((l + r) >> 1);
if (check(mid)) {
ans = mid;
r = mid - 1;
} else
l = mid + 1;
}
return ans;
}
void main() {
n = read(), R = read(), G = read();
for (int i = 1; i <= n; ++i) w[i] = read();
sort(w + 1, w + 1 + n);
if (R + G >= n) printf("1\n");
else printf("%d\n", binary_search());
}
}
int main() {
steven24::main();
return 0;
}
/*
3 1 1
22
1
7
*/
H.飞离地球
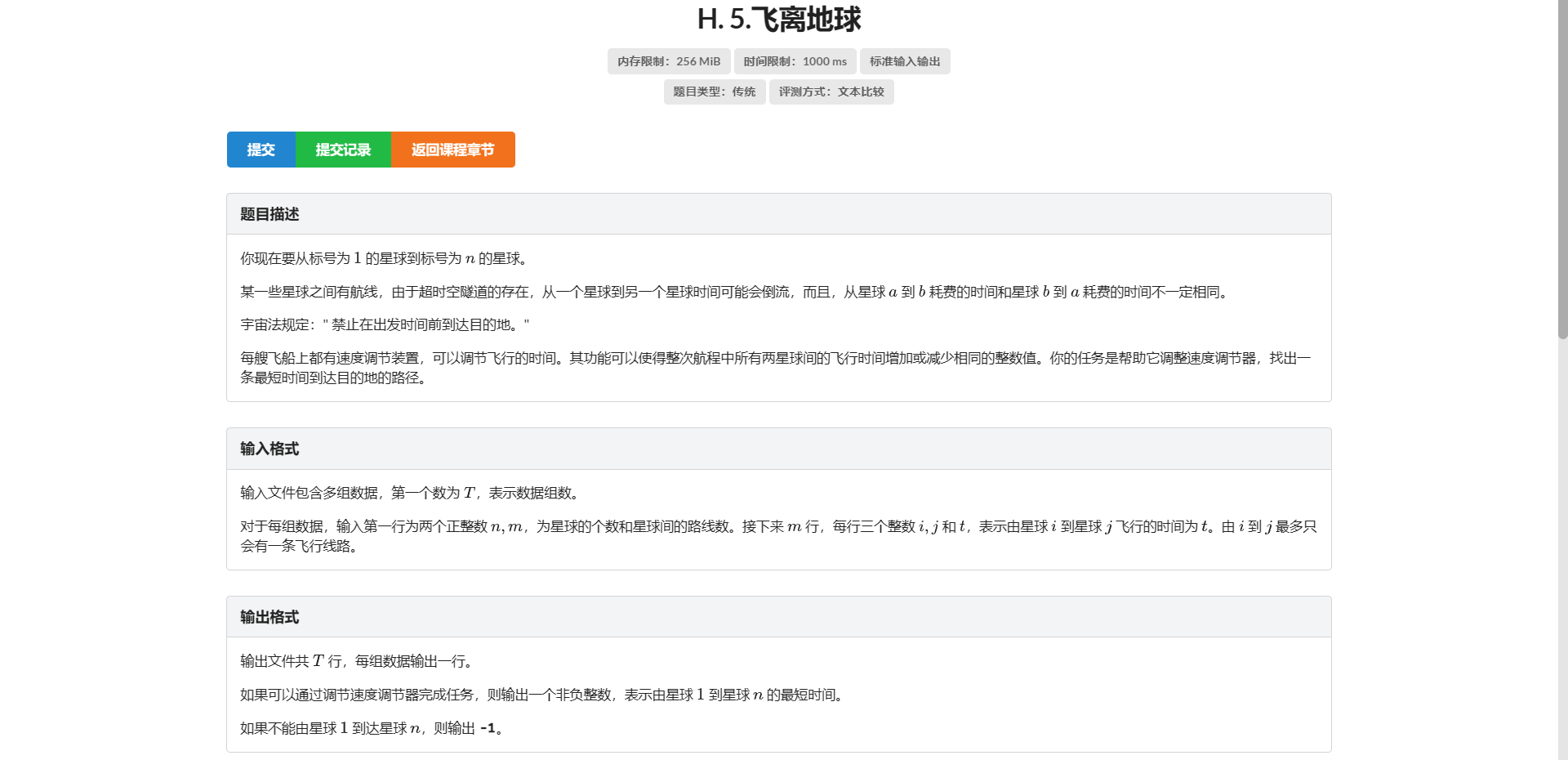
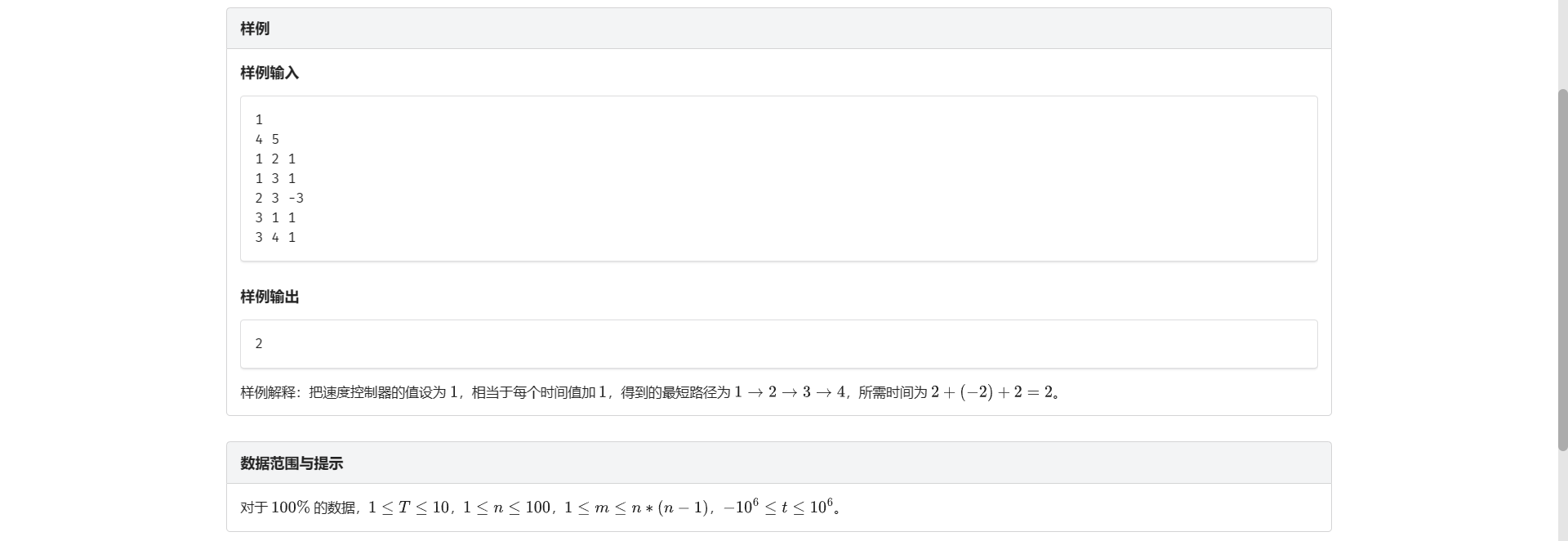
刚开始看到这题以为途中路过的每个点的 dis 都不能为负 结果觉得这玩意不具有单调性
考虑 wqs 二分 无果
考虑二分答案 无果
去看题解 发现只是满足 \(dis_n \ge 0\) 并且不存在负环即可
那就一眼二分了
几个需要注意的点:
- 不在 1 - n 这段路径上的负环会影响 spfa 所以先预处理出所有从 1 出发能到达并且能到达 n 的点
- spfa 判负环 常看常新
vis[y] = vis[now] + 1;
if (vis[y] >= n) return 0;
- 多测清空 T不大可以直接偷懒 memset
然后就一遍写过了 基本功了属于是(
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace steven24 {
const int N = 105;
const int M = 10005;
int head[N], to[M], nxt[M], len[M], cnt;
int _head[N], _to[M], _nxt[M], _cnt;
ll dis[N];
bool vis1[N], vis2[N]; //表示能从1到达和能到达n
bool exist[N];
int vis[N];
ll ans;
int n, m, T;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
void init() {
memset(head, 0, sizeof head);
memset(_head, 0, sizeof _head);
memset(vis1, 0, sizeof vis1);
memset(vis2, 0, sizeof vis2);
cnt = _cnt = 0;
ans = -1;
}
inline void add_edge(int x, int y, int z) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
len[cnt] = z;
_to[++_cnt] = x; //建反图方便找出能到达n的点
_nxt[_cnt] = _head[y];
_head[y] = _cnt;
}
void dfs1(int x) { //1能到达的点
vis1[x] = 1;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (vis1[y]) continue;
dfs1(y);
}
}
void dfs2(int x) { //能到达n的点
vis2[x] = 1;
for (int i = _head[x]; i; i = _nxt[i]) {
int y = _to[i];
if (vis2[y]) continue;
dfs2(y);
}
}
bool spfa(int x) {
memset(dis, 0x3f, sizeof dis);
memset(exist, 0, sizeof exist);
vis[1] = 0;
queue<int> q;
q.push(1);
dis[1] = 0;
exist[1] = 1;
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = head[now]; i; i = nxt[i]) {
int y = to[i];
if (!vis1[y] || !vis2[y]) continue;
if (dis[y] > dis[now] + len[i] + x) {
dis[y] = dis[now] + len[i] + x;
if (!exist[y]) {
exist[y] = 1;
q.push(y);
}
vis[y] = vis[now] + 1;
if (vis[y] >= n) return 0;
}
}
exist[now] = 0;
}
return dis[n] >= 0 && dis[n] != 0x3f3f3f3f3f3f3f3f;
}
void binary_search() {
int l = -1e6, r = 1e6;
int mid;
while (l <= r) {
mid = ((l + r) >> 1);
if (spfa(mid)) {
ans = dis[n];
r = mid - 1;
} else
l = mid + 1;
}
}
void main() {
T = read();
while (T--) {
init();
n = read(), m = read();
for (int i = 1; i <= m; ++i) {
int x, y, z;
x = read(), y = read(), z = read();
add_edge(x, y, z);
}
dfs1(1);
dfs2(n);
binary_search();
printf("%lld\n", ans);
}
}
}
int main() {
steven24::main();
return 0;
}
/*
1
4 5
1 2 1
1 3 1
2 3 -3
3 1 1
3 4 1
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号