YBTOJ 1.2贪心算法
A.奶牛晒衣服
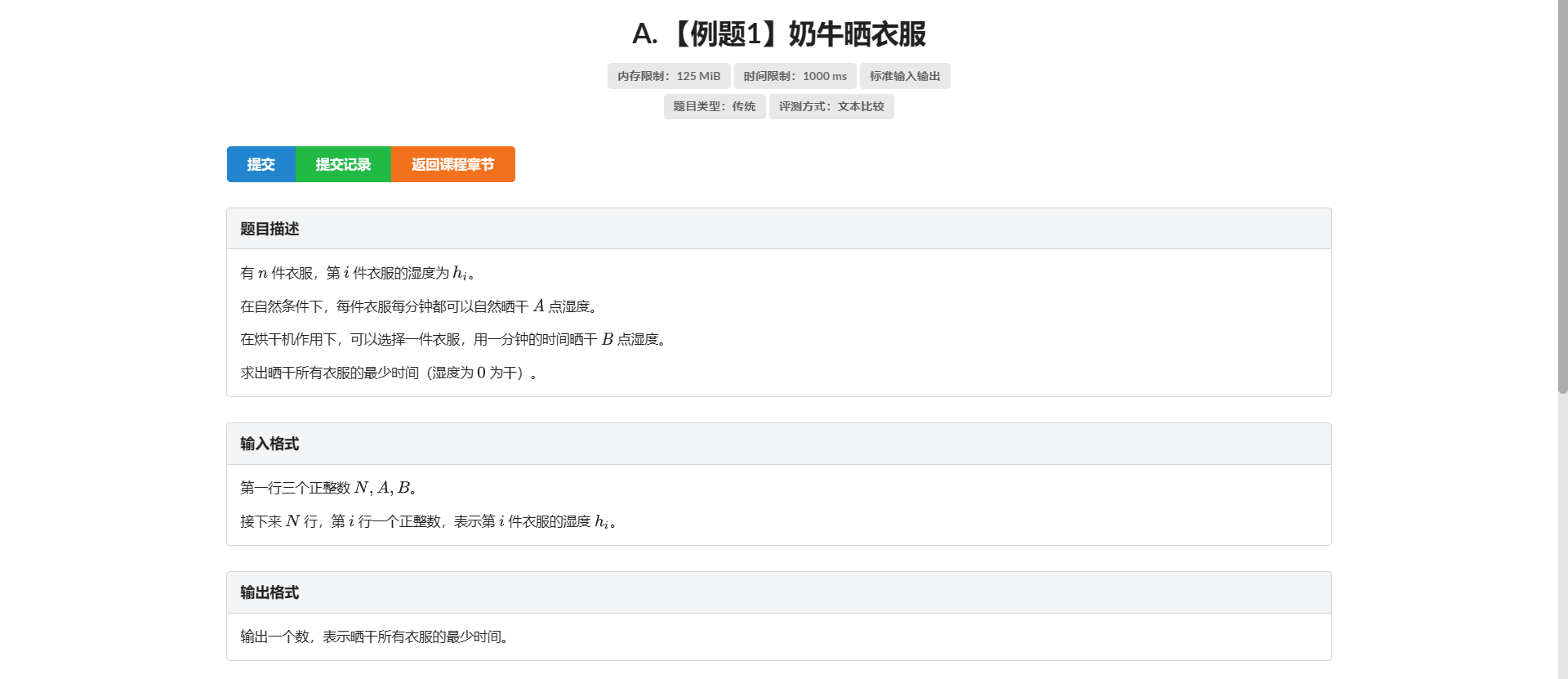
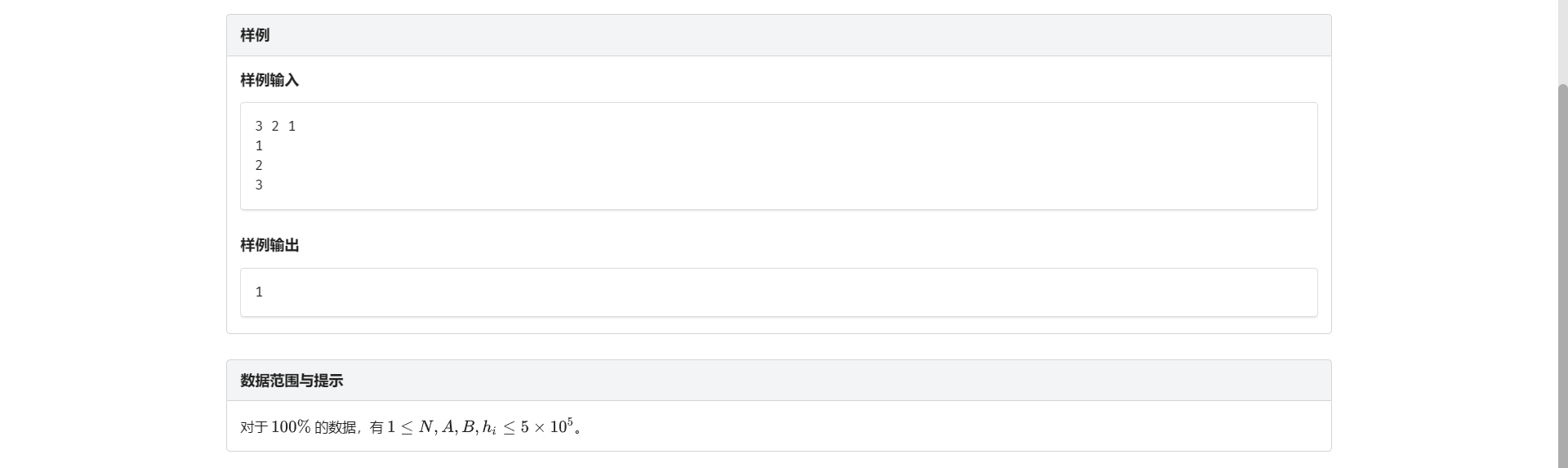
很容易想到一个贪心思路:每次把烘干机会给当前湿度最大的衣服
我们假设有一次没烘干当前湿度最大的衣服
因为总时间取决于湿度最大的衣服
所以最后湿度最大的衣服湿度一定会更大点
那么要么总时间不变 要么会变长
一定不会更优
注意这题 \(n \le 5 * 10^5\) 需要采用 \(O(nlogn)\) 的大根堆
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 0721;
int h[N];
int n, a, b, ans;
priority_queue<int, vector<int>, less<int> > q;
int main() {
scanf("%d%d%d", &n, &a, &b);
for (int i = 1; i <= n; ++i) {
scanf("%d", &h[i]);
q.push(h[i]);
}
while (1) {
int now = q.top();
q.pop();
if (now <= ans * a)
break;
++ans;
now -= b;
q.push(now);
}
printf("%d", ans);
return 0;
}
B.雷达装置
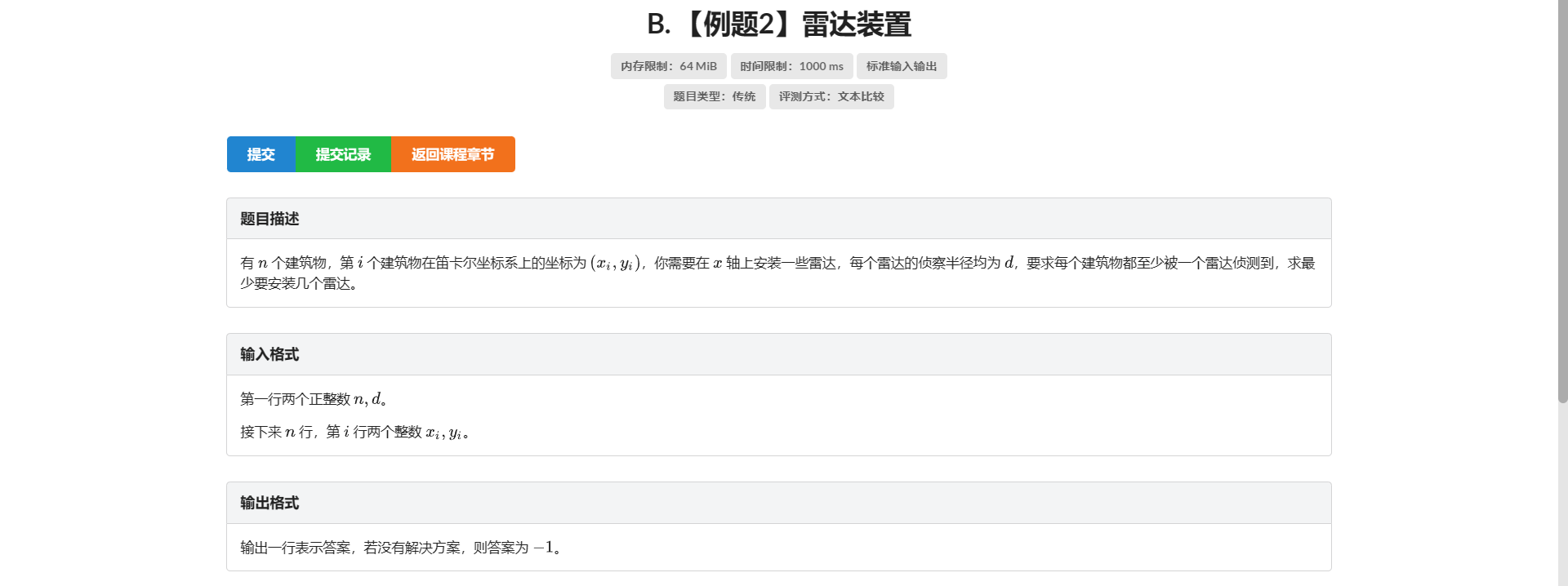
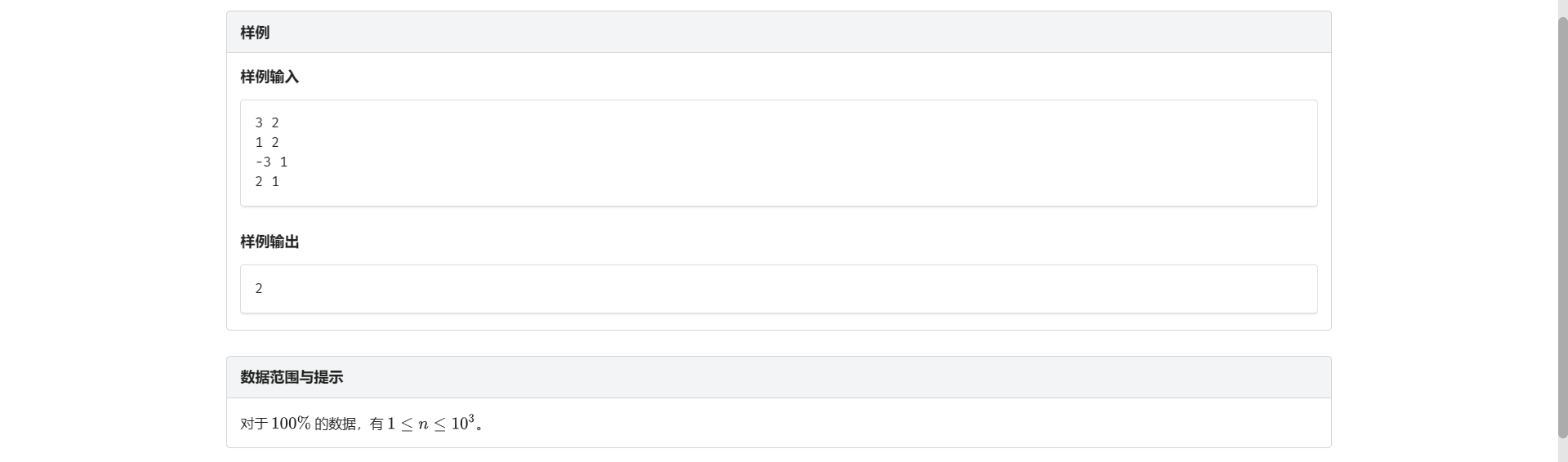
首先二维不是很好考虑 思考能不能把信息全转化到 \(x\) 轴上
发现当 \(d\) 固定的时候 对于一个点 能覆盖到它的雷达是 \(x\) 轴上一段连续区间
我们考虑将点都转化成 \(x\) 轴上若干段区间
然后就是区间覆盖的板子了
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 0721;
int x[N], y[N];
struct node {
double l, r;
} a[N];
int n, d, ans = 1;
void cl(int id) {
double dis = sqrt(d * d - y[id] * y[id]);
a[id].l = x[id] - dis;
a[id].r = x[id] + dis;
}
bool cmp(node x1, node x2) { return x1.r < x2.r; }
int main() {
scanf("%d%d", &n, &d);
for (int i = 1; i <= n; ++i) {
scanf("%d%d", &x[i], &y[i]);
if (y[i] > d) {
printf("-1");
return 0;
}
cl(i);
}
sort(a + 1, a + 1 + n, cmp);
double last = a[1].r;
for (int i = 2; i <= n; ++i) {
if (a[i].l <= last && a[i].r >= last)
continue;
else
++ans, last = a[i].r;
}
printf("%d", ans);
return 0;
}
C.畜栏预定
一道很友善的贪心题
很容易想到先把牛按 \(l\) 排序 然后把畜栏按结束时间排序
每次取出结束最早的畜栏 并与当前的牛比较
如果在这头牛吃草之前畜栏就空出来 就把这头牛安排到这个畜栏
否则 就需要新加一个畜栏
证明:假如我们不是把牛放到结束时间最早的畜栏
由于牛吃草结束的时间不变 这个畜栏结束的时间不变
对于开始时间 这个畜栏更容易出现忙不过来的情况 就可能出现多的畜栏
所以选结束最早的畜栏一定不会更劣
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 5e4 + 0721;
struct cow {
int l, r, id;
} a[N];
int n, cnt, ans[N];
bool cmp(cow x1, cow x2) { return x1.l < x2.l; }
struct node {
int id, now;
friend bool operator<(node x1, node x2) { return x1.now > x2.now; }
};
priority_queue<node> q;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d%d", &a[i].l, &a[i].r), a[i].id = i;
sort(a + 1, a + 1 + n, cmp);
cnt = 1, ans[1] = 1, q.push((node){ cnt, a[1].r });
for (int i = 2; i <= n; ++i) {
int prs = q.top().id;
int last = q.top().now;
// cout<<a[i].l<<" "<<prs<<" "<<last<<" " ;
if (a[i].l > last) {
q.pop();
ans[a[i].id] = prs;
last = a[i].r;
q.push((node){ prs, last });
} else {
++cnt;
ans[a[i].id] = cnt;
q.push((node){ cnt, a[i].r });
}
// cout<<ans[i]<<endl;
}
printf("%d\n", cnt);
for (int i = 1; i <= n; ++i) printf("%d\n", ans[i]);
return 0;
}
D.荷马史诗

哈夫曼堆 经典例题可以看P1090 [NOIP2004 提高组] 合并果子
其实就是一个除了最后一层以外满叉的多叉树
我们给每个叉赋予一个编码
那么显然层数越浅的 其编码越短
所以我们要让出现次数多的尽可能的放在上层
所以我们每次把 \(k\) 个最小的元素合并起来 然后丢回堆里 重复此过程
但是要注意一个问题 就是有可能在第一层出现总堆数不够 \(k\) 个的情况 那就没法把这层占满 显然是血亏的 所以我们要另外加一些空点
因为每次合并少了 \(k - 1\) 个果子 一共要把 \(n\) 个果子合并起来所以少了一共 \(n - 1\) 只有当 \(n - 1\) 是 \(k - 1\) 的整数倍时 才能使每次合并都时满 \(k\) 的合并
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
struct node {
ll val, dep;
friend bool operator<(node x, node y) {
if (x.val != y.val)
return x.val > y.val;
else
return x.dep > y.dep;
}
};
priority_queue<node> q;
int main() {
int n, k;
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; ++i) {
ll w;
scanf("%lld", &w);
q.push((node){ w, 0 });
}
while ((q.size() - 1) % (k - 1) != 0) {
q.push((node){ 0, 0 });
}
ll ans = 0;
while (q.size() > 1) {
ll hi = 0;
ll sum = 0;
for (int i = 1; i <= k; ++i) {
sum += q.top().val;
hi = max(hi, q.top().dep);
q.pop();
}
ans += sum;
q.push((node){ sum, hi + 1 });
}
printf("%lld\n%lld",ans,q.top().dep);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号