YBTOJ 1.1递推算法

A.错排问题

考虑将第 \(i\) 个数插进来 假设我们放到了 \(k\) 位置
那么我们现在要把 \(k\) 拿出来找个新地方放
一种情况是把 \(k\) 放到 \(i\) 的位置 那么剩下 \(i - 2\) 个数就是一个错排
另一种是把 \(k\) 放到那 \(i - 2\) 个点里 那么就相当于把第 \(i - 1\) 个数插进来
又因为 \(k\) 可以在那 \(i - 1\) 个点里随便选 所以要乘上 \((i - 1)\)
转移式 \(f[i] = (i - 1) * (f[i - 1] + f[i - 2])\)

点击查看代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;

const int N = 25;
ll f[N];

int main() {
    int n;
    scanf("%d", &n);
    f[1] = 0, f[2] = 1;
    for (int i = 3; i <= n; ++i) f[i] = (f[i - 1] + f[i - 2]) * (i - 1);

    printf("%lld", f[n]);

    return 0;
}

---

B.传球游戏

考虑传球的转移 显然会从左边和右边两个人传过来
设 \(f[i][j]\) 表示传了 \(j\) 次第 \(i\) 个人手里有球的方案数
那么我们就有 \(f[i][j] = f[i - 1][j - 1] + f[i + 1][j - 1]\)
注意特判第 \(1\) 个人和第 \(n\) 个人

点击查看代码

#include <bits/stdc++.h>
using namespace std;

const int N = 31;
int f[N][N];
int n, m;

int main() {
    scanf("%d%d", &n, &m);
    f[1][0] = 1;

    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (j == 1)
                f[j][i] = f[j + 1][i - 1] + f[n][i - 1];
            else if (j == n)
                f[j][i] = f[j - 1][i - 1] + f[1][i - 1];
            else
                f[j][i] = f[j - 1][i - 1] + f[j + 1][i - 1];
        }
    }

    printf("%d", f[1][m]);

    return 0;
}

---

C.数的划分

设 \(f[i][j]\) 表示将 \(i\) 分成 \(j\) 份的方案数
那么我们显然有：

• 当 \(i < j\) 时 \(f[i][j] = 0\)
• 当 \(i = j\) 时 \(f[i][j] = 1\)

我们讨论 \(i > j\) 的情况

• 当这 \(j\) 堆里至少有一堆是 \(1\) 时 我们把一堆的 \(1\) 拿掉 就是把 \(i - 1\) 分成 \(j - 1\) 堆
• 当这 \(j\) 堆里一个 \(1\) 都没有时 我们把所有的堆都减 \(1\) 那么就是把 \(i - j\) 分成 \(j\) 堆

所以转移式为 \(f[i][j] = f[i - 1][j - 1] + f[i - j][j]\)

点击查看代码

#include <bits/stdc++.h>
using namespace std;

int ans[201][7];
int n, k;

int main() {
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= k; ++j) {
            if (i == j)
                ans[i][j] = 1;
            if (i > j)
                ans[i][j] = ans[i - 1][j - 1] + ans[i - j][j];
        }
    }

    printf("%d", ans[n][k]);

    return 0;
}

---

D.栈的问题

（这题其实是个卡特兰
设 \(f[i]\) 表示 \(i\) 个木块进出栈的方案数
我们枚举最后一个出栈的元素 \(k\)
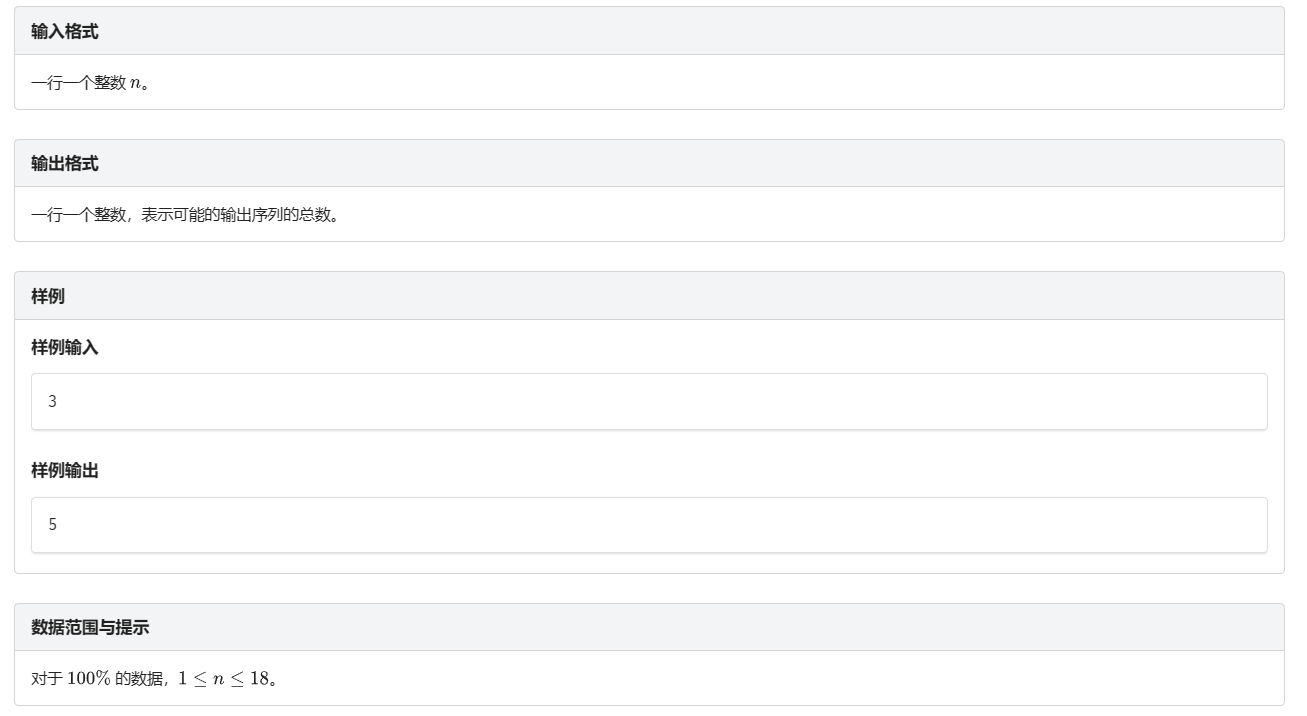
显然这样的话全过程就是 \(k\) 之前的 \(k - 1\) 个元素先进栈再出栈 然后 \(k\) 进栈 然后 \(k\) 之后的 \(n - k - 1\) 个元素进栈再出栈 然后 \(k\) 出栈
我们枚举这个 \(k\) 就有
\(f[i] += f[k - 1] * f[i - k - 1]\)

点击查看代码

#include <bits/stdc++.h>
#define ll long long

using namespace std;

const int N = 25;
ll f[N];
int n;

int main() {
    scanf("%d", &n);
    f[0] = f[1] = 1;
    for (int i = 2; i <= n; ++i) {
        for (int j = 0; j < i; ++j) {
            f[i] += f[j] * f[i - j - 1];
        }
    }
    printf("%lld",f[n]);

    return 0;
}