线段树学习笔记
Part1： 建树 单点修改 区间求和
关于线段树：假如我们有这样一个数列 3 3 2 8 0 7 2 1
那我们就可以建一个线段树 大概长这样：
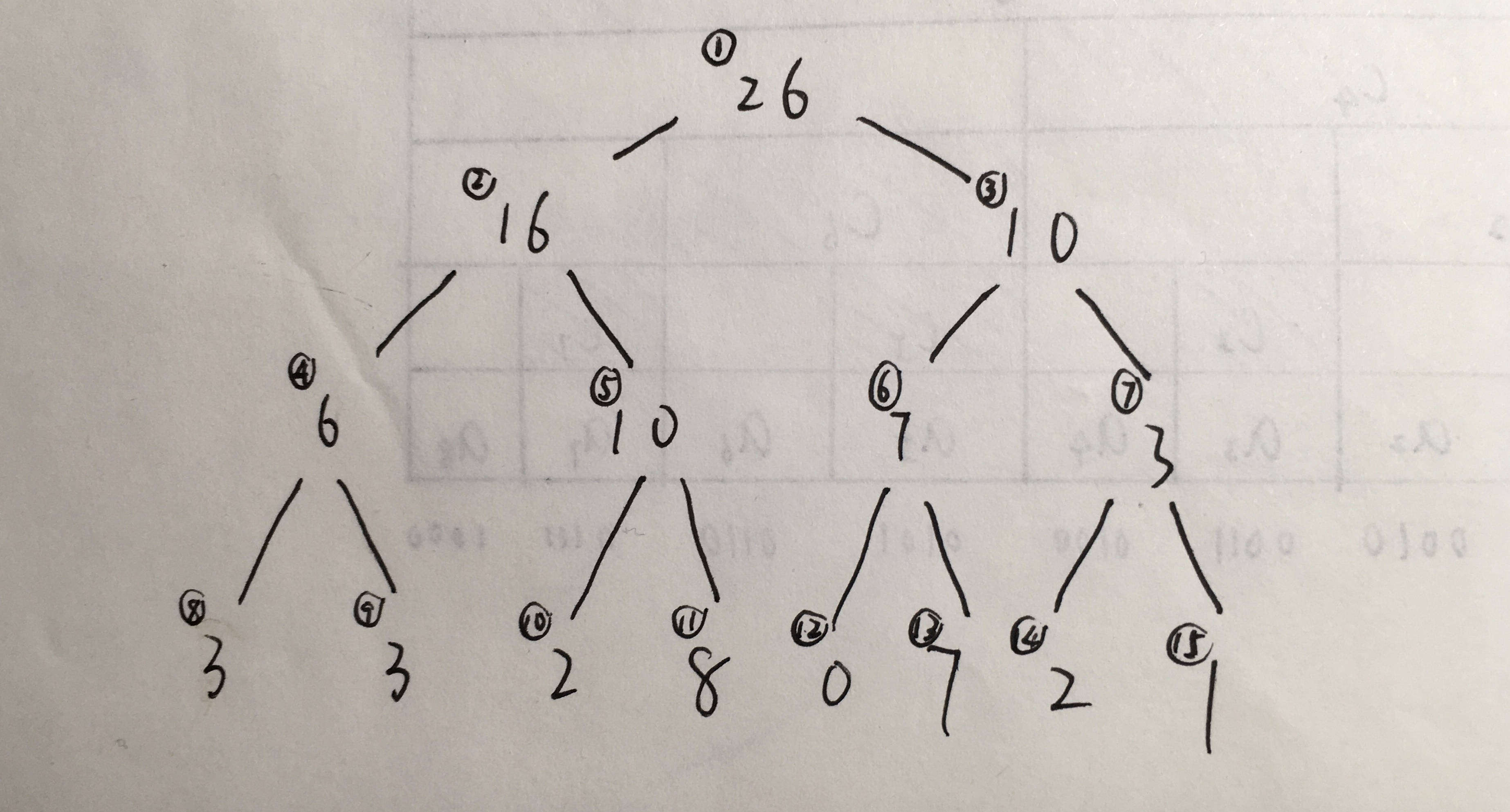
由图可知 编号为i的左子树编号为2i 右子树编号为2i+1
我们用k代表根 用ls代表k的左子树 用rs代表k的右子树 mid为当前k涵盖区间的中点 则有：
建树
容易看出 对于一个根k 它的值即为ls与rs的和 所以我们先递归ls 再递归r's 最后处理k
每次递归长度减少一半 当区间长度为1时返回原数组中对应位置
单点修改
我们首先查找出这个点处在的叶的位置 然后从下往上更新
区间求和
假设我们要求的区间为[x,y] 那么我们考虑当前k所包含的区间[l,r]与[x,y]的关系：
1.[x,y]包含[l,r] 那么就直接将s[k]加入答案中
2.[x,y]不包含[l,r] 那么就以mid为界 将[x,y]分成两段区间 然后分别递归ls rs
看到这你可能会问：这和树状数组不是差不多吗 为什么要花这么大的码量来写这个？我直接写树状数组不香吗？
别急 线段树的强大才真正开始：
Part2：区间加法 区间求和
定义一个lazy数组 lazy[k]表示k这段区间内整体加lazy[k]
那么如果我们要修改的区间已经包含了当前k的区间 我们直接打上lazy[k]标记就走
这样我们就有了两个新的函数：
adl函数：将k的lazy标加上v
我们先将s[k]增加(r-l+1)*v （即k中包含的元素个数）
然后更新lazy标
pushdown函数：将k的lazy标下传给ls rs
我们先下传
然后清空lazy标
所以我们现在除了built函数外 有了三个函数：adl pushdown pushup
然后我们再来看区间加法和区间查询 大概可以概括为以下模板：
1.若[x,y]包含[l,r] 则对k处理后直接return
2.否则 将k的lazy标记下传 这里就要用到pushdown（新增）
3.分成两段处理 和前面一样
4.更新k 用pushup（半新增）
（好像更好记了）
代码如下：
区间加法
区间查询
但事实上 线段树的强大远不止这些：
Part3：区间加乘
定义数组lazy1 lazy2 分别表示k这段区间整体加/乘了lazy1[k]/lazy2[k]
这时我们就要修改我们的adl函数和pushdown函数
pushdown倒好说 就是将原来 lazy[k] = 0 变为对两个lazy数组都进行还原
（其实也不好说 我写的时候写的 lazy2[k] = 0 然后de了半天）
对于adl函数 我们需要将原来的v改为v1和v2 表示k这段区间加了v1乘了v2
然后我们考虑v1v2对s[k]的影响：v1还是使s[k]增加了 v1*(r-l+1)
而v2 它会使 s[k] *= v2
同时我们还要考虑两个lazy数组的更新
lazy2好说 *=v2 就行
但对于lazy1 我们应先乘后加： lazy1[k] = lazy1[k] * v2 + v1
为什么是这样呢 我们可以举个例子：假设我们对k先 +4 再 *2 最后 +3
那么第一步后 lazy1[k] = 4 并且它总共乘了2 总共加了3
那么新的lazy1数组就应为 4 * 2 + 3
最后还有一点小小的需要注意的地方：lazy2的初值应为1 这步可以单独处理 也可以塞进built函数中
adl代码
pushdown代码
