P2014 选课 （ 树上背包 ）
先看树上背包的板子：
假设我们的树长这样：
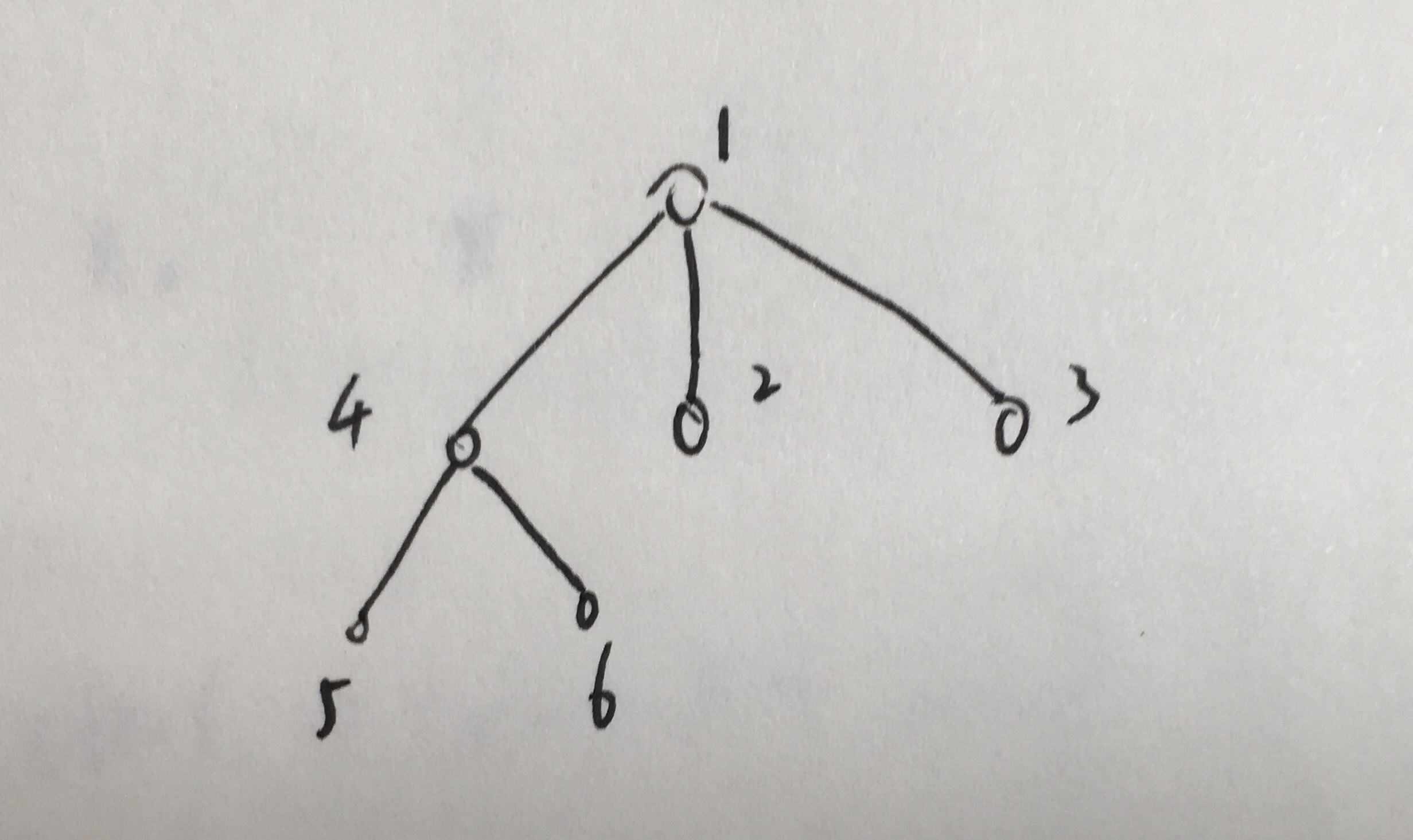
那么其实我们就有个比较朴素的想法：
对一个结点 对它的儿子们进行背包dp
比如对于1号点 我们就可以对2号 3号进行背包dp
问题是4号咋整？
我们不难发现 对于4号点 我们有4 45 46 456四种不同的选择 每一种对应的体积与价值各不相同
那我们就把数组扩展到二维：
用f[i][j]表示以i为根的子树中 总体积为j的时候能带来的最大价值
那么状态转移方程怎么想（以下为个人理解）
可以发现 我们对一个根节点的所有儿子进行背包dp的时候 同一个儿子只能选一个状态（即f[i][j]中对于同一个i只能选一个j）
所以我们可以把它看成分组背包：
对于一个根节点 它的每一个儿子都为一组 每组只能选一个
然后如果你还记得分组背包的代码：
（从oi wiki上扒的）
那么其实可以类比一下 树上背包的代码就出来了：
这里特别注意一下 由于我们的父亲是由儿子转移过来的 所以先dfs儿子再进行下一步
现在状态设计好了 状态转移方程有了 别忘了写边界条件：
(一定要记得w[x]后面的都要填上）
完整代码就不贴了（其实是我懒得写了）
时间复杂度为O(n\(m^2\)) （单次转移O(\(m^2\)) dfs有n次）
现在在看这题 好像就是一个w[i]全为1的树上背包
一算复杂度 \(300^3\) 还真能过
以下为本题代码：
当然了 这题这题还有个 n , m <= 1,000 的版本 那这个显然就过不去了
为此我们可以对这种w[i]全为1的情况做一个优化：
我们再回头看原来那个状态转移方程：
我们思考这样两个问题：k是什么 j又是什么
答：k是给这个子树分配的节点个数 j是当前这个根节点容纳的节点个数
那么我们不难发现 其实k是不会超过这个子树大小 同理j也不会超过已经合并过的子树的大小
所以我们可以动态维护一个数组siz[i]表示以i为根节点的树的大小
然后每一次dp的时候siz[i] += siz[i的儿子]（噢对了别忘了初始化 所有的节点最开始的siz都为1 ）
这样我们就可以减少k和j的枚举次数了
具体代码如下：
upd：上面那玩意复杂度还是会退化 这里贴一个复杂度正确的代码
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
dfs(y, x);
for (int j = siz[x]; j >= 0; --j) { //注意写法 不然复杂度会退化
for (int k = 0; k <= siz[y]; ++k) {
f[x][j + k][1] = min(f[x][j + k][1], f[x][j][1] + f[y][k][1]);
f[x][j + k][1] = min(f[x][j + k][1], f[x][j][1] + f[y][k][0]);
f[x][j + k][0] = min(f[x][j + k][0], f[x][j][0] + f[y][k][0]);
}
}
siz[x] += siz[y];
}
此方法复杂度为O(mn)
关于复杂度证明：
首先感觉这就是个挺玄乎的玩意 你只要知道它复杂度是这个就行（（
这里提供一个本人想到的不是很严谨也可能不是很正确的证法：
这里简化下题意：单纯将根的所有儿子合并 所用的时间复杂度 设树的大小为n 则复杂度应为O(\(n^2\))
upd：这玩意假的 看个乐就行
