蓝桥杯 2017 C++ A 题解
部分题 所有的题见链接
链接:https://pan.baidu.com/s/1v9bRsavm1VSI08S-A67qWQ
提取码:pxfy
T1 标题:迷宫
X星球的一处迷宫游乐场建在某个小山坡上。
它是由10x10相互连通的小房间组成的。
房间的地板上写着一个很大的字母。
我们假设玩家是面朝上坡的方向站立,则:
L表示走到左边的房间,
R表示走到右边的房间,
U表示走到上坡方向的房间,
D表示走到下坡方向的房间。
X星球的居民有点懒,不愿意费力思考。
他们更喜欢玩运气类的游戏。这个游戏也是如此!
开始的时候,直升机把100名玩家放入一个个小房间内。
玩家一定要按照地上的字母移动。
迷宫地图如下:
------------
UDDLUULRUL
UURLLLRRRU
RRUURLDLRD
RUDDDDUUUU
URUDLLRRUU
DURLRLDLRL
ULLURLLRDU
RDLULLRDDD
UUDDUDUDLL
ULRDLUURRR
------------
请你计算一下,最后,有多少玩家会走出迷宫?
而不是在里边兜圈子。
请提交该整数,表示走出迷宫的玩家数目,不要填写任何多余的内容。
如果你还没明白游戏规则,可以参看一个简化的4x4迷宫的解说图:
p1.png
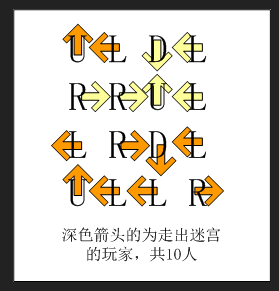
#include <iostream>
#include <string>
#include <stdio.h>
using namespace std;
//string ss [10]="UDDLUULRUL,UURLLLRRRU,RRUURLDLRD,RUDDDDUUUU,URUDLLRRUU,DURLRLDLRL,ULLURLLRDU,RDLULLRDDD,UUDDUDUDLL,ULRDLUURRR";
//string ss [4]="ULDL,RRUL,LRDL,ULLR";
#define N 10
char ss[N][N];
int ans = 0 ;
void check(int i , int j, int cnt){
if(cnt>100) return ;
char c = ss[i][j];
if(c=='U') --i;
if(c=='D') ++i;
if(c=='L') --j;
if(c=='R') ++j;
if(i<0 || i >N-1 || j<0 || j>N-1){
ans++;return ;
}
check(i,j,++cnt);
}
int main(){
//输入
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N; j++)
{
cin >> ss[i][j];
}
getchar();
}
/*
for(int i = 0; i < 4; i++)
{
for(int j = 0; j < 4; j++)
{
cout << ss[i][j];
}
cout<<endl;
}
*/
for(int i=0;i<N;++i){
for(int j=0;j<N;++j){
check(i,j,0);
}
}
cout <<ans<<endl;
return 0;
}
/*
ULDL
RRUL
LRDL
ULLR
10
UDDLUULRUL
UURLLLRRRU
RRUURLDLRD
RUDDDDUUUU
URUDLLRRUU
DURLRLDLRL
ULLURLLRDU
RDLULLRDDD
UUDDUDUDLL
ULRDLUURRR
31
*/
T2 标题:跳蚱蜢
如图 p1.png 所示:
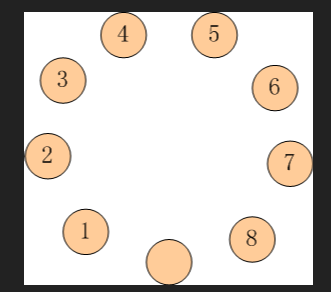
有9只盘子,排成1个圆圈。
其中8只盘子内装着8只蚱蜢,有一个是空盘。
我们把这些蚱蜢顺时针编号为 1~8
每只蚱蜢都可以跳到相邻的空盘中,
也可以再用点力,越过一个相邻的蚱蜢跳到空盘中。
请你计算一下,如果要使得蚱蜢们的队形改为按照逆时针排列,
并且保持空盘的位置不变(也就是1-8换位,2-7换位,...),至少要经过多少次跳跃?
注意:要求提交的是一个整数,请不要填写任何多余内容或说明文字。
#include<iostream>
#include<string>
#include<set>
#include<queue>
//青蛙跳格子,采用裸广搜的方法,几秒可以出答案,但是有时间限制就不行了
//将青蛙跳看作是,圆盘跳动,这样就只有一个变量在变化了
//将圆盘看成是0,初始序列用012345678表示,在广搜的时候用set判一下重
using namespace std;
struct node {
string str;//局面字符串
int pos;//0的位置也就是空盘子
int step;//到达这个局面的步数
node(string str, int pos, int step) : str(str), pos(pos), step(step) {}
};
int N = 9;
set<string> visited;//已经搜索过的局面 主要为了去重
queue<node> q;//用户来广搜的队列
//四个方向 也就是四个邻居的添加
void insertq(node no, int i)//node为新的局面,i为移动方式
{
string s = no.str;
swap(s[no.pos], s[(no.pos + i + 9) % 9]);//将0和目标位置数字交换
//取模是为了模拟循环的数组
//if (visited.count(s) == 0)//如果没有搜索过这个局面
if(visited.end() == visited.find(s))
{
visited.insert(s);
node n(s, (no.pos + i + 9) % 9, no.step + 1);
q.push(n);
}
}
int main() {
//初始 0空盘在0位置 走过步数0
node first("012345678", 0, 0);
q.push(first);
while (!q.empty()) {
node temp = q.front(); //去第一个 因为之前的pop出去了
if (temp.str == "087654321") { //结束
cout << temp.step;
break;
} else {
//四种跳法 相当于有四个邻居
insertq(temp, 1);
insertq(temp, -1);
insertq(temp, 2);
insertq(temp, -2);
q.pop(); //四个邻居添加完之后 就可以滚蛋了
}
}
}
T3 标题:魔方状态
二阶魔方就是只有2层的魔方,只由8个小块组成。
如图p1.png所示。
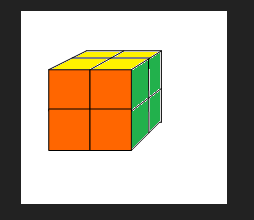
小明很淘气(是真的淘气!),他只喜欢3种颜色,所有把家里的二阶魔方重新涂了颜色,如下:
前面:橙色
右面:绿色
上面:黄色
左面:绿色
下面:橙色
后面:黄色
请你计算一下,这样的魔方被打乱后,一共有多少种不同的状态。
如果两个状态经过魔方的整体旋转后,各个面的颜色都一致,则认为是同一状态。
请提交表示状态数的整数,不要填写任何多余内容或说明文字。
#include <bits/stdc++.h>
using namespace std;
typedef char st[8][7];
st state[2000000];
set<string> all;
st begin={{"oybbgb"},{"oygbbb"},{"bygbby"},{"bybbgy"},{"obbogb"},{"obgobb"},{"bbgoby"},{"bbbogy"}};
//st begin={{"oooooo"},{"oooooo"},{"oooooo"},{"oooooo"},{"oooooo"},{"oooooo"},{"oooooo"},{"oooooo"}};
//只有一个颜色的魔方 ans=1
//st begin={{"rykkbk"},{"rygkkk"},{"kygkko"},{"kykkbo"},{"rkkwbk"},{"rkgwkk"},{"kkgwko"},{"kkkwbo"}};
//正常2阶魔方状态 r红 y黄 b蓝 g绿 w白 o橙 k黑(红对橙,白对黄,蓝对绿,颜色相近的相对)这里白为底 前为红
//需要将state大小改为4000000
//这个测试用例跑了20分钟左右 560M内存 ans=3674160 与实际二阶魔方状态数相同 见下截图
int front, tail;
void ucell(char *a){swap(a[0], a[2]); swap(a[2], a[5]); swap(a[5], a[4]);}
void rcell(char *a){swap(a[1], a[0]); swap(a[0], a[3]); swap(a[3], a[5]);}
void fcell(char *a){swap(a[2], a[1]); swap(a[1], a[4]); swap(a[4], a[3]);}
void u(st &s)//顶层顺时针旋转
{
ucell(s[0]);
ucell(s[1]);
ucell(s[2]);
ucell(s[3]);
swap(s[1], s[0]);
swap(s[2], s[1]);
swap(s[3], s[2]);
}
void uwhole(st &s)//整个魔方从顶部看 顺时针转 用于判重
{
u(s);
ucell(s[4]);
ucell(s[5]);
ucell(s[6]);
ucell(s[7]);
swap(s[5], s[4]);
swap(s[6], s[5]);
swap(s[7], s[6]);
}
void f(st &s)//前面一层 顺时针转
{
fcell(s[0]);
fcell(s[1]);
fcell(s[4]);
fcell(s[5]);
swap(s[1], s[5]);
swap(s[0], s[1]);
swap(s[4], s[0]);
}
void fwhole(st &s)//整个魔方从前面看 顺时针转 用于判重
{
f(s);
fcell(s[2]);
fcell(s[6]);
fcell(s[7]);
fcell(s[3]);
swap(s[2], s[6]);
swap(s[3], s[2]);
swap(s[7], s[3]);
}
void r(st &s)//魔方右层顺时针转
{
rcell(s[1]);
rcell(s[2]);
rcell(s[6]);
rcell(s[5]);
swap(s[2], s[1]);
swap(s[5], s[1]);
swap(s[6], s[5]);
}
void rwhole(st &s)//整个魔方从右边看 顺时针转 用于判重
{
r(s);
rcell(s[0]);
rcell(s[3]);
rcell(s[4]);
rcell(s[7]);
swap(s[3], s[7]);
swap(s[0], s[3]);
swap(s[4], s[0]);
}
string convert(st &s)//魔方状态二维字符数组 转化为string
{
string ss;
for(int i=0; i<8; i++)ss+=s[i];
return ss;
}
bool try_to_insert(int tail)//判重
{
st k;
memcpy((void*)k, (void*)state[tail], sizeof(state[tail]));
for(int i=0; i<4; i++)
{
fwhole(k);
for(int j=0; j<4; j++)
{
uwhole(k);
for(int q=0; q<4; q++)
{
rwhole(k);
if(all.count(convert(k))==1)
{
return false;
}
}
}
}
all.insert(convert(k));
return true;
}
int main()
{
front=0,tail=1;
all.insert(convert(begin));
memcpy((void*)state[0],(void*)begin,sizeof(begin));
while(front!=tail)
{
//对当前状态分别模拟三种操作U R F 然后判重
for(int i=0; i<3; i++)
{
memcpy((void*)state[tail], (void*)state[front], sizeof(state[front]));
if(i==0)
{
u(state[tail]);
if(try_to_insert(tail))tail++;
}
else if(i==1)
{
r(state[tail]);
if(try_to_insert(tail))tail++;
}
else if(i==2)
{
f(state[tail]);
if(try_to_insert(tail))tail++;
}
}
front++;
}
cout<<front<<endl;
return 0;
}
//ans 229878
T4 标题:方格分割
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
如图:p1.png, p2.png, p3.png 就是可行的分割法。
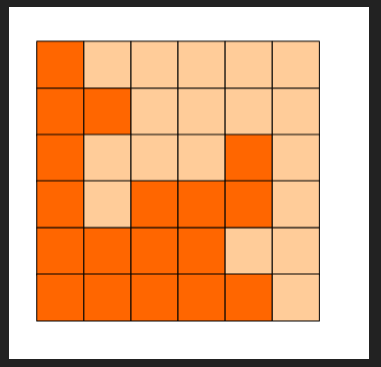

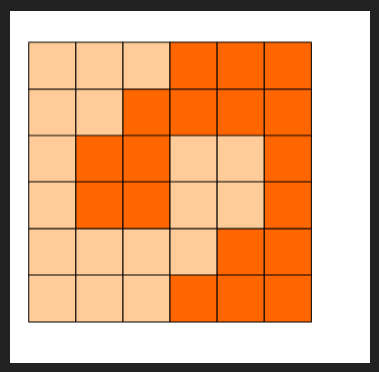
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
#include <iostream>
using namespace std;
//方向
int dir[4][2]{
{-1,0}, //左
{1,0}, // 右
{0,-1}, // 上
{0,1},// 下
} ;
int vis[7][7]; //一条边上7个点
int ans ;
void dfs(int x ,int y){
if(x==0 || y==0 || x==6 || y==6){ //剪到边缘就可以结束了 因为再往左右剪无效了 剪的是边
ans++ ;
return ;
}
vis[x][y] =1 ; //当前点
vis[6-x][6-y]=1; //对称点
for(int i=0;i<4;++i){
int nx = x + dir[i][0];
int ny = y + dir[i][1];
//nx ny 为新坐标
if(nx<0 || nx>6 || ny<0 || ny>6){
continue ;
}
if(vis[nx][ny]!=1){
dfs(nx,ny);
}
}
//当前点的四个方向都走完了 可以滚蛋了
vis[x][y] =0 ; //当前点
vis[6-x][6-y]=0; //对称点
}
int main(){
dfs(3,3);
cout<<ans/4 <<endl ;
return 0 ;
}
T7 描述:正则问题
考虑一种简单的正则表达式:
只由 x ( ) | 组成的正则表达式。
小明想求出这个正则表达式能接受的最长字符串的长度。
例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是: xxxxxx,长度是6。
输入
----
一个由x()|组成的正则表达式。输入长度不超过100,保证合法。
输出
----
这个正则表达式能接受的最长字符串的长度。
例如,
输入:
((xx|xxx)x|(x|xx))xx
程序应该输出:
6
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include <xxx>
不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std ;
char s[100];
int pos = 0; //整体必须有一个指针位置 一直往后遍历
int f(){
int m =0;
int tmp = 0 ;
while(pos < strlen(s)){
if(s[pos]=='('){
pos++;
tmp += f(); //再另外开辟 来算括号 括号套括号就继续开
}
if(s[pos]=='x'){
tmp++;
pos++ ;
}
if(s[pos]=='|'){
++pos;
m = max(m,tmp);
tmp = 0;
}
if(s[pos]==')'){
pos++;
m = max(m,tmp);//有可能这个括号里面是存在 | 的 所以这个括号结束后得结算再返回
return m;
}
}
m= max(m,tmp);
return m;
}
int main(){
cin>>s ;
int ans ;
ans = f();
cout<<ans ;
//((xx|xxx)x|(x|xx))xx 6
}
T8 标题:包子凑数(与2013年买不到的数 类似)
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼,分别能放3、4和5个包子。当顾客想买11个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼,分别能放4、5和6个包子。而顾客想买7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入
----
第一行包含一个整数N。(1 <= N <= 100)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100)
输出
----
一个整数代表答案。如果凑不出的数目有无限多个,输出INF。
例如,
输入:
2
4
5
程序应该输出:
6
再例如,
输入:
2
4
6
程序应该输出:
INF
样例解释:
对于样例1,凑不出的数目包括:1, 2, 3, 6, 7, 11。
对于样例2,所有奇数都凑不出来,所以有无限多个。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include <xxx>
不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
/*
a*x+b*y=c
a,b两个数如果互质 那么一定有不可取到的c的最大值
相反 如果a,b不互质 那么有无穷多个数取不到
*/
#include <iostream>
#include <stdio.h>
using namespace std;
int n,g;
bool f[10000]; //存每个数是否能取到
//求a,b 最大公约数
int gcd(int a , int b){
if(b == 0)return a;
//如果互质 最后就会返回 1 否则中途就会返回最大公约数
return gcd(b,a%b);
}
int main (){
cin>>n;
int a[n+1];
f[0]=true;
for(int i=1 ; i<=n ; ++i){
cin>>a[i];
//每输进来一个 就求当前的最大公约数
if(i ==1)g=a[i];
else g = gcd(a[i],g);
//每增加一个 就更新后面可以得到的所有数
for(int j=0;j<10000;++j){
//这样 倍数的通过往后移 都会被标记可取到
if(f[j])f[a[i]+j]=true;
}
}
//得输入完毕后再判断 不能阻断了输入
if(i!=1 && g!=1){
//并不互质
cout<<"INF"<<endl;
return 0 ;
}
int ans =0;
for(int j=0;j<1000;++j){
if(!f[j])ans++;
}
cout << ans <<endl;
}
T9 标题: 分巧克力
儿童节那天有K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有N块巧克力,其中第i块是Hi x Wi的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出K块巧克力分给小朋友们。切出的巧克力需要满足:
1. 形状是正方形,边长是整数
2. 大小相同
例如一块6x5的巧克力可以切出6块2x2的巧克力或者2块3x3的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小Hi计算出最大的边长是多少么?
输入
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含两个整数Hi和Wi。(1 <= Hi, Wi <= 100000)
输入保证每位小朋友至少能获得一块1x1的巧克力。
输出
输出切出的正方形巧克力最大可能的边长。
样例输入:
2 10
6 5
5 6
样例输出:
2
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include <xxx>
不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
/*
a*x+b*y=c
a,b两个数如果互质 那么一定有不可取到的c的最大值
相反 如果a,b不互质 那么有无穷多个数取不到
*/
#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <math.h>
using namespace std;
int main (){
//n块待切的巧克力 k个小朋友
int n , k ;
cin>>n>>k ;
int a[n][2];
//输入
for(int i=0 ; i<n ; ++i){
cin>>a[i][0]>>a[i][1];
}
/*
int mi;
int all;
for(int i=0 ; i<n ; ++i){
mi = min(a[i][0],a[i][1]);
}
for(int j=mi ; j>0 ; --j){
all = 0;
for(int i=0 ; i<n ; ++i){
all += (a[i][0]/j)*(a[i][1]/j);
}
if(all>=k){
cout<< j << endl;return 0 ;
}
}
//27 points
*/
//二分 优化
int ans =0;
int l = 1 ;
int r = 100001;
int middle = (l+r)/2 ;
while(l<=r){
middle = (l+r)/2 ;
int all = 0;
for(int i=0 ; i<n ; ++i){
all += (a[i][0]/middle)*(a[i][1]/middle);
}
if(all>=k){
l = middle + 1 ;
ans = middle ;
}else r = middle -1;
}
cout<<ans<<endl;
return 0 ;
}



