NOIp 2018 普及组
T1标题统计
传送门
题目描述
凯凯刚写了一篇美妙的作文,请问这篇作文的标题中有多少个字符? 注意:标题中可能包含大、小写英文字母、数字字符、空格和换行符。统计标题字 符数时,空格和换行符不计算在内。
输入输出格式
输入格式:
输入文件只有一行,一个字符串 $ s $ 。
输出格式:
输出文件只有一行,包含一个整数,即作文标题的字符数(不含空格和换行符)。
输入输出样例
输入样例#1:
234
输出样例#1:
3
输入样例#2:
Ca 45
输出样例#2:
4
说明
【数据规模与约定】
规定 $ |s| $ 表示字符串 $ s $ 的长度(即字符串中的字符和空格数)。
对于 $ %40 $ 的数据,$ 1 ≤ |s| ≤ 5 $ ,保证输入为数字字符及行末换行符。
对于 $ %80 $ 的数据,$ 1 ≤ |s| ≤ 5 $ ,输入只可能包含大、小写英文字母、数字字符及行末换行符。
对于 $ %100% $ 的数据,$ 1 ≤ |s| ≤ 5 $ ,输入可能包含大、小写英文字母、数字字符、空格和行末换行符。
这个题感觉大水题吧,会用 $ gets $ 输入感觉问题就不大 。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <map>
#include <set>
#define re register
using namespace std ;
char s[10] ;
int ans , len ;
int main() {
gets(s) ;
len = strlen(s);
for(re int i = 0 ; i < len ; ++i) {
if(s[i] >= '0' && s[i] <= '9') ans ++ ;
if(s[i] >= 'A' && s[i] <= 'Z') ans ++ ;
if(s[i] >= 'a' && s[i] <= 'z') ans ++ ;
}
printf("%d\n" , ans) ;
return 0 ;
}
T2龙虎斗
传送门啦
题目描述
轩轩和凯凯正在玩一款叫《龙虎斗》的游戏,游戏的棋盘是一条线段,线段上有 $ n $ 个兵营(自左至右编号 $ 1 \sim n $ ),相邻编号的兵营之间相隔 $ 1 $ 厘米,即棋盘为长度为 $ n-1 $ 厘米的线段。$ i $ 号兵营里有 $ c[i] $ 位工兵。
下面图 1 为 $ n=6 $ 的示例:
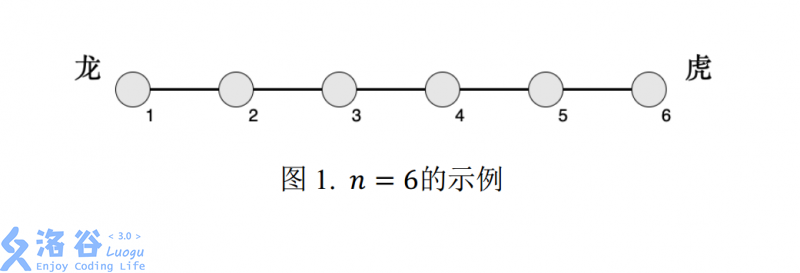
轩轩在左侧,代表“龙”;凯凯在右侧,代表“虎”。 他们以 $ m $ 号兵营作为分界, 靠左的工兵属于龙势力,靠右的工兵属于虎势力,而第 $ m $ 号兵营中的工兵很纠结,他们不属于任何一方。
一个兵营的气势为:该兵营中的工兵数 $ \times $ 该兵营到 $ m $ 号兵营的距离;参与游戏 一方的势力定义为:属于这一方所有兵营的气势之和。
下面图 2 为 $ n = 6,m = 4 $ 的示例,其中红色为龙方,黄色为虎方:
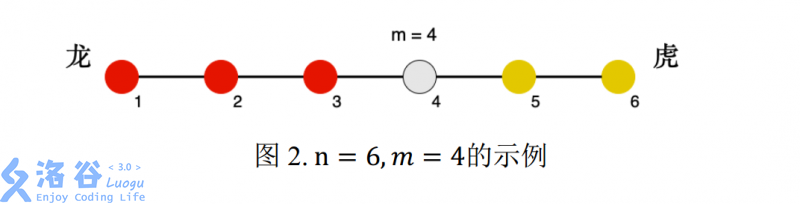
游戏过程中,某一刻天降神兵,共有 $ s_1 $ 位工兵突然出现在了 $ p_1 $ 号兵营。作为轩轩和凯凯的朋友,你知道如果龙虎双方气势差距太悬殊,轩轩和凯凯就不愿意继续玩下去了。为了让游戏继续,你需要选择一个兵营 $ p_2 $ ,并将你手里的 $ s_2 $ 位工兵全部派往 兵营 $ p_2 $ ,使得双方气势差距尽可能小。
注意:你手中的工兵落在哪个兵营,就和该兵营中其他工兵有相同的势力归属(如果落在 $ m $ 号兵营,则不属于任何势力)。
输入输出格式
输入格式:
输入文件的第一行包含一个正整数 $ n $ ,代表兵营的数量。
接下来的一行包含 $ n $ 个正整数,相邻两数之间以一个空格分隔,第 $ i $ 个正整数代 表编号为 $ i $ 的兵营中起始时的工兵数量 $ c[i] $ 。
接下来的一行包含四个正整数,相邻两数间以一个空格分隔,分别代表 $ m,p_1,s_1,s_2 $ 。
输出格式:
输出文件有一行,包含一个正整数,即 $ p_2 $ ,表示你选择的兵营编号。如果存在多个编号同时满足最优,取最小的编号。
输入输出样例
输入样例#1:
6
2 3 2 3 2 3
4 6 5 2
输出样例#1:
2
输入样例#2:
6
1 1 1 1 1 16
5 4 1 1
输出样例#2:
1
说明
【输入输出样例 1 说明】
见问题描述中的图 2。
双方以 $ m=4 $ 号兵营分界,有 $ s_1=5 $ 位工兵突然出现在 $ p_1=6 $ 号兵营。 龙方的气势为:
$ 2 \times (4-1)+3 \times (4-2)+2 \times (4-3) = 142×(4−1)+3×(4−2)+2×(4−3)=14 $
虎方的气势为:
$ 2 \times (5 - 4) + (3 + 5) \times (6 - 4) = 182×(5−4)+(3+5)×(6−4)=18 $
当你将手中的 $ s_2 = 2 $ 位工兵派往 $ p_2 = 2 $ 号兵营时,龙方的气势变为:
$ 14 + 2 \times (4 - 2) = 1814+2×(4−2)=18 $
此时双方气势相等。
【输入输出样例 2 说明】
双方以 $ m = 5 $ 号兵营分界,有 $ s_1 = 1 $ 位工兵突然出现在 $ p_1 = 4 $ 号兵营。
龙方的气势为:
$ 1 \times (5 - 1) + 1 \times (5 - 2) + 1 \times (5 - 3) + (1 + 1) \times (5 - 4) =11 $
虎方的气势为:
$ 16 \times (6 - 5) = 16 $
当你将手中的 $ s_2 = 1 $ 位工兵派往 $ p_2 = 1 $ 号兵营时,龙方的气势变为:
$ 11 + 1 \times (5 - 1) = 15 $
此时可以使双方气势的差距最小。
【数据规模与约定】
$ 1 < m < n,1 ≤ p_1 ≤ n $ 。
对于 $ %20 $ 的数据,$ n = 3,m = 2, c_i = 1, s_1,s_2 ≤ 100 $ 。
另有 $ %20 $ 的数据,$ n ≤ 10, p_1 = m, c_i = 1, s_1,s_2 ≤ 100 $ 。
对于 $ %60 $ 的数据,$ n ≤ 100, c_i = 1, s_1,s_2 ≤ 100 $ 。
对于 $ %80 $ 的数据,$ n ≤ 100, c_i,s_1,s_2 ≤ 100 $ 。
对于 $ %100 $ 的数据, $ n≤10^5
,c_i,s_1,s_2≤10^9 $ 。
分析:
这个题是很纯的模拟题,就是各种符号有点乱,注意不要打错就好了。模拟的时候在每个点上都加上一次试试,不会超时,而且实现更简单,维护一个最小的差。
需要注意的是如果我们加上这些士兵之后比原来的差值还大,那就放 $ m $ 号点上就好了( $ m $ 点加没加无所谓)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <map>
#include <queue>
#define re register
using namespace std ;
const int maxn = 1e5 + 3 ;
inline long long read() {
char ch = getchar();
long long f = 1 , x = 0;
while(ch > '9' || ch < '0') { if(ch == '-') f = -1 ; ch = getchar () ;}
while(ch >= '0' && ch <= '9') { x = (x << 1) + (x << 3 ) + ch - '0' ; ch = getchar() ;}
return x * f;
}
long long n , c[maxn] , m , p1 , s1 , s2 , p2 ;
long long now1 , now2 ;
int main () {
//freopen("lhd.in","r",stdin);
n = read() ;
for(re int i = 1 ; i <= n ; ++ i) {
c[i] = read() ;
}
m = read() ; p1 = read() ; s1 = read() ; s2 = read() ;
c[p1] += s1 ;
for(re int i = 1 ; i <= m - 1 ; ++ i) now1 += (m - i) * c[i] ;
for(re int i = m + 1 ; i <= n ; ++ i) now2 += (i - m) * c[i] ;
//printf("\n%lld\n%lld\n\n" , now1 , now2) ;
long long cha = 1e9 ;
long long f = 0 ;
if(now1 == now2) printf("%lld\n" , m) ;
else if(now1 > now2) {
for(re int i = m + 1 ; i <= n ; ++ i) {
if(now2 + (i - m) * s2 == now1) {
f = i ;
break ;
}
else {
if(cha > abs(now2 + (i - m) * s2 - now1)) {
cha = abs(now2 + (i - m) * s2 - now1) ;
f = i ;
}
}
}
if(now1 - now2 < cha) printf("%lld\n" , m) ;
else printf("%lld\n" , f) ;
}
else {
for(re int i = 1 ; i <= m - 1 ; ++ i) {
if(now1 + (m - i) * s2 == now2) {
f = i ;
break ;
}
else {
if(cha > abs(now1 + (m - i) * s2 - now2)) {
f = i ;
cha = abs(now1 + (m - i) * s2 - now2) ;
}
}
}
if(now2 - now1 < cha) printf("%lld\n" , m) ;
else printf("%lld\n" , f) ;
}
return 0 ;
}
对称二叉树
传送门
题目描述
一棵有点权的有根树如果满足以下条件,则被轩轩称为对称二叉树:
- 二叉树;
- 将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值,节点外的 id 表示节点编号。
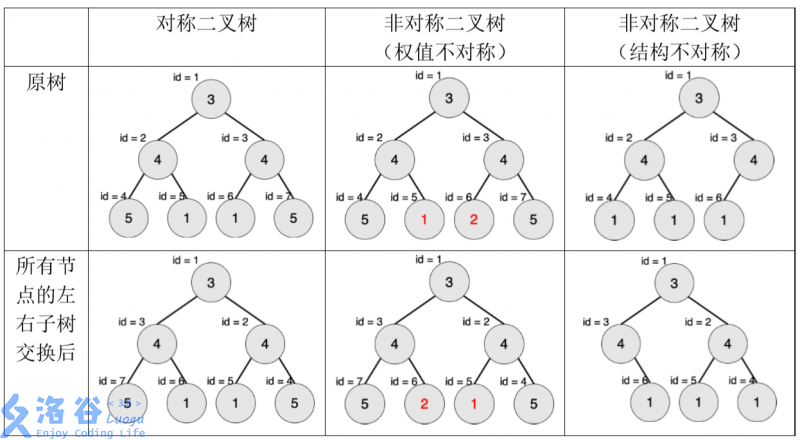
现在给出一棵二叉树,希望你找出它的一棵子树,该子树为对称二叉树,且节点数 最多。请输出这棵子树的节点数。
注意:只有树根的树也是对称二叉树。本题中约定,以节点 $ T $ 为子树根的一棵“子 树”指的是:节点 $ T $ 和它的全部后代节点构成的二叉树。
输入输出格式
输入格式:
第一行一个正整数 $ n $ ,表示给定的树的节点的数目,规定节点编号 $ 1 \sim n $ ,其中节点 $ 1 $ 是树根。
第二行 $ n $ 个正整数,用一个空格分隔,第 $ i $ 个正整数 $ v_i $ 代表节点 $ i $ 的权值。
接下来 $ n $ 行,每行两个正整数 $ l_i , r_i $ ,分别表示节点 $ i $ 的左右孩子的编号。如果不存在左 / 右孩子,则以 $ -1 $ 表示。两个数之间用一个空格隔开。
输出格式:
输出文件共一行,包含一个整数,表示给定的树的最大对称二叉子树的节点数。
输入输出样例
输入样例#1:
2
1 3
2 -1
-1 -1
输出样例#1:
1
输入样例#2:
10
2 2 5 5 5 5 4 4 2 3
9 10
-1 -1
-1 -1
-1 -1
-1 -1
-1 2
3 4
5 6
-1 -1
7 8
输出样例#2:
3
【数据规模与约定】
共 $ 25 $ 个测试点。 $ v_i ≤ 1000 $ 。
测试点 $ 1 \sim 3, n ≤ 10 $ ,保证根结点的左子树的所有节点都没有右孩子,根结点的右 子树的所有节点都没有左孩子。
测试点 $ 4 \sim 8 , n ≤ 10 $ 。
测试点 $ 9 \sim 12, n ≤ 10^5 $ ,保证输入是一棵“满二叉树” 。
测试点 $ 13 \sim 16, n ≤ 10^5 $ ,保证输入是一棵“完全二叉树”。
测试点 $ 17 \sim 20, n ≤ 10^5 $ ,保证输入的树的点权均为 1。
测试点 $ 21 \sim 25, n ≤ 10^6 $ 。
本题约定:
层次:节点的层次从根开始定义起,根为第一层,根的孩子为第二层。树中任一节 点的层次等于其父亲节点的层次加 $ 1 $ 。
树的深度:树中节点的最大层次称为树的深度。
满二叉树:设二叉树的深度为 $ h $ ,且二叉树有 $ 2h-1 $ 个节点,这就是满二叉树。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
using namespace std ;
#define re register
const int maxn = 1e6 + 3 ;
inline int read () {
int f = 1 , x = 0 ;
char ch = getchar() ;
while(ch > '9' || ch < '0') {if(ch == '-') f = -1 ; ch = getchar () ;}
while(ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + ch - '0' ; ch = getchar () ;}
return x * f ;
}
int n , v[maxn] ;
int l[maxn] , r[maxn] ;
int ch[maxn][2] , c[maxn] , ans ;
//c[]记录当前最大的节点数
bool check (int a , int b) {
//判断两个点是否对称
if(a == b) return true ; //同一个点也算对称
//if(!a || !b) return false ;
if(v[a] != v[b]) return false ; //值不相等不算
return (check(ch[a][1] , ch[b][2]) && check(ch[a][2] , ch[b][1]) ) ;
}
inline void dfs (int x) {
if(!x) return ;
dfs(ch[x][1]) ;
dfs(ch[x][2]) ;
c[x] = 1 + c[ch[x][1]] + c[ch[x][2]] ;
//该点最大节点数 = 本身 1 + 左儿子的节点数 + 右儿子的节点数 ;
v[x] = v[x] + v[ch[x][1]] + v[ch[x][2]] ;
//为了判断(两个子树中的总值不相等也说明不对称)
if(ans < c[x] && check(ch[x][1] , ch[x][2])) //左右儿子对称
ans = c[x] ;
}
int main () {
n = read () ;
for(re int i = 1 ; i <= n ; ++ i) {
v[i] = read () ;
}
v[0] = 1005 ;
for(re int i = 1 ; i <= n ; ++ i) {
l[i] = read () ;
if(l[i] != -1) ch[i][1] = l[i] ;
r[i] = read () ;
if(r[i] != -1) ch[i][2] = r[i] ;
}
dfs(1) ;
printf("%d\n" , ans ) ;
return 0 ;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号