简单线性回归
简单线性回归
虽然简单线性回归对于现实世界的问题几乎不具有可用性，但是理解简单线性回归是理解许多其他模型的关键。
简单线性回归（一元）
假设你希望了解披萨的价格。你可能会简单地查看菜单。但是这里，我们将基于能观测到的披萨的属性或者说解释变量，来预测披萨的价格。让我们来对披萨的尺寸和价格之间的关系进行建模。首先，我们将使用 scikit-learn 编写一段程序，通过提供的披萨尺寸来预测其价格。接着我们将讨论简单线性回归如何运行以及如何将其泛化来解决其他类型的问题。
假设已经记录下了已经吃过的披萨的直径和价格。表中的观测值组成了我们的训练数据。
| 训练实例 | 直径（单位：英寸） | 价格（单位：美元） |
|---|---|---|
| 1 | 6 | 7 |
| 2 | 8 | 9 |
| 3 | 10 | 13 |
| 4 | 14 | 17.5 |
| 5 | 18 | 18 |
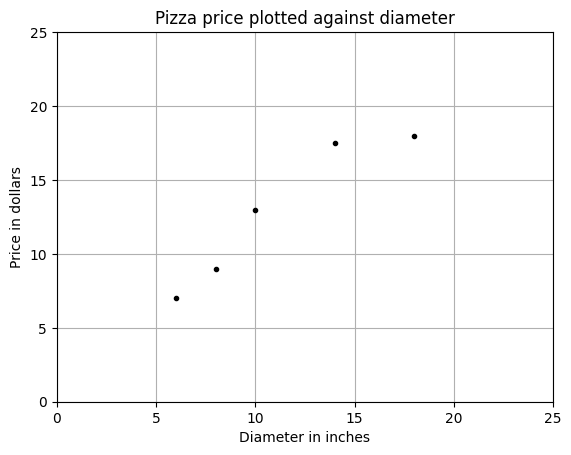
从训练数据的图中我们可以看出披萨的直径和价格之间存在正相关关系，这应该可以由自己吃披萨的经验所证实。随着披萨直径的增加，它的价格通常也会上涨。下面使用了简单线性回归来对这个关系进行建模，并且讨论简单线性回归是如何运行的。
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, y)
test_pizza = np.array([[12]])
predicted_price = model.predict(test_pizza)[0]
print(f"A 12' pizza should cost: ${predicted_price:.2f}")
简单线性模型假设响应变量和解释变量之前存在线性关系，它使用一个被称为超平面的线性面来对这种关系进行建模。一个超平面是一个子空间，它比组成它的环绕空间小一个维度。在简单线性回归中共有两个维度，一个维度表示响应变量，另一个维度表示解释变量。因此，回归超平面只有一个维度，一个一维的超平面是一条直线。
LinearRegression 类是一个估计器。估计器基于观测到的数据预测一个值。在 scikit-learn 中，所有的估计器都实现了 fit 方法和 predict 方法。前者用于学习模型的参数，后者使用学习到的参数来预测一个解释变量对应的响应变量值。尝试新的模型只需要简单地修改一行代码。LinearRegression 的 fit 方法学习了下面方程的简单线性回归模型的参数：
用代价函数评价模型的拟合性
代价函数，也被称为损失函数，它用于定义和衡量一个模型的误差。由模型预测出的价格和在训练数据集中观测到的披萨价格之间的差值被称为残差或者训练误差。在测试数据中预测值和观测值之间的差值叫作预测误差或者测试误差。
我们可以通过最小化残差的和来生成最佳披萨价格预测器。也就是说，对于所有训练数据而言，如果模型预测的响应变量都接近观测值，那么模型就是拟合的，这种衡量模型拟合的方法叫作残差平方和（RSS）代价函数。在形式上，该函数通过对所有训练数据的残差平方求和来衡量模型的拟合性。RSS 由下面的方程计算出，其中 \(y_i\) 是观测值，\(f(x_i)\) 是预测值：
评价模型
我们可以使用一些衡量方法来评估模型的预测能力。在此我们使用一种叫作 R 方的方法来评估披萨价格预测器。R 方，也被称为决定系数，它用来衡量数据和回归线的贴近程度。计算 R 方的方法有多种，在简单线性回归模型中，R 方等于皮尔森积差相关系数（PPMCC）的平方，也被称为皮尔森相关系数 r 的平方。使用该计算方法，R 方必须是 0 和 1 之间的正数，其原因很直观：如果 R 方描述的是由模型解释的响应变量中的方差的比例，这个比例不能大于 1 或者小于 0。其他一些计算方法，包括 scikit-learn 库使用的方法，不使用皮尔森相关系数 r 的平方公式计算 R 方。如果模型的表现非常差，由这些计算方法求出的 R 方可能为负值。了解性能指标的局限性非常重要，R 方对于异常值尤其敏感，当新的特征增加到模型中时，它常常会出现异样的增长。
>>> from sklearn.linear_model import LinearRegression
>>> import numpy as np
>>> X_train = np.array([6, 8, 10, 14, 18]).reshape(-1, 1)
>>> y_train = [7, 9, 13, 17.5, 18]
>>> X_test = np.array([8, 9, 11, 16, 12]).reshape(-1, 1)
>>> y_test = [11, 8.5, 15, 18, 11]
>>> model = LinearRegression()
>>> model.fit(X_train, y_train)
LinearRegression()
>>> r_squared = model.score(X_test, y_test)
>>> print(r_squared)
0.6620052929422553
>>>
