算法笔记：数论基础

CW一月游记 Day1

好像混了一天..大概听懂了一丢丢...数论之前一直没有时间学 非常尴尬

顺便自己写一下ing ing...

基础讲解

• 如果\(a\)除以非\(0\)整数\(b\)商为整数，且余数为0 -> 我们就说\(a\)能被\(b\)整除或者\(b\)能够整除\(a\) 记作 \(b|a\)
• 整除的基本定理 [如果\(a|b\) \(a|c\) 那么 \(a|bc\)] [如果\(a|b\),那么对于所有整数\(c\),\(a|bc\)] [若\(a|b\),\(b|c\),则\(a|c\)]
• 每一个正整数都可以唯一表示为素数（质数）的乘积
• 如果两个数\(a\)、\(b\)除以一个\(c\)的余数相等，说\(a\)与\(b\)关于\(%c\)同余，记作\(a≡b(mod c)\) -> \(a≡b(mod c)\)成立的充要条件是\((a-b)=k*c\)

最大公约数和最小公倍数

• 设两个不为\(0\)的正整数\(a\)、\(b\),能使\(d|a\) && \(d|b\)，那么\(d\)就是关于a与b的最大公约数，用\(gcd(a,b)\)表示，或者记为\((a,b)\)
• 设两个不为\(0\)的正整数\(a\)、\(b\),能使\(a|d\) && \(b|d\)，那么\(d\)就是关于a与b的最小公倍数，用\(lcm(a,b)\)表示，或者记为\([a,b]\)
• 定理：\(ab = gcd(a,b) * lcm(a,b)\)
• 如果\(gcd(a,b) = 1\) 则\(a,b\)互质

最大公约数和最小公倍数的定理证明

• 使用唯一分解定理，设
  $a = p_{1}^{a_{1}}p_{2}{a_{2}}...p_{n}^{a_{n}} \( \)b = p_{1}^{b_{1}}p_{2}{b_{2}}...p_{n}^{b_{n}} $
• 那么就有
  \(lcm(a,b)=p_{1}^{max(a_{1},b_{1})}p_{2}^{max(a_{2},b_{2})}...p_{n}^{max(a_{n},b_{n})}\)
  \(gcd(a,b)=p_{1}^{min(a_{1},b_{1})}p_{2}^{min(a_{2},b_{2})}...p_{n}^{min(a_{n},b_{n})}\)

最大公约数的求解

• 名称：欧几里得算法（辗转相除法）
• 利用公式 \(gcd(a,b) = gcd(b,a mod b)\),时间复杂度\((logb)\)
• 证明：
  设\(r = a%b,r = a-kb\)
  设\(d\)是\(a,b\)的公约数，则\(d|a,d|b\),则\(d|r\)
  则\(d\)是\(b,a%b\)的公约数
  设\(d\)是\(b,a%b\)的公约数，同理可证\(d\)是\(a,b\)的公约数
  则\(gcd(a,b)=gcd(b,a%b)\)
• 代码：(递归版)

int gcd(int x,int y)
{
    return b?gcd(y,x%y):x
}

质数筛法（\(2n\)写法 直接上代码）

void int_prime(int x)
{
    for (int i=2;i<=x;i++)
    {
        if(!flag[i]) pre[too++] = i;
        for (int j=0;j<tot && pre[j]<=m/i;j++)
        {
            flag[i*pre[j]] = 1;
            if(i % pre[j] == 0) break;
        }
    }
}

质数筛法例题

CodeForces 114E Double Happiness
hdu 1999 不可摸数

拓展欧几里得

• 婓蜀定理：对于不完全为\(0\)的非负整数\(a,b\),\(gcd(a,b)\)表示\(a,b\)的最大公约数，必然存在整数对\(x,y\),使得\(gcd(a,b)=ax+bx\)
• 欧几里得算法静止的状态是：\(a=gcd,b=0\)即当\(x=1,y=0\)时，这就是最终状态

拓展欧几里得证明

• 设\(x,y\)和\(x1,y1\)时两组解,且满足：
  由\(a*x+b*y = gcd(a,b)\)
  \(b*x_{1}+(aModb)*y_{1} = gcd(b,aModb)\)
  得\(a*x+b*y=b*x_{1}+(a%b)*y_{1}\)
  设\(k=a/b,r=a%b\),则\(r=a-k*b\),代入上式得
  \(a*x+b*y=b*x_{1}+(a-a/b*b)*y_{1}\)
  \(a*x+b*y=a*y_{1}+b*(x_{1}-a/b*y_{1})\)
  得\(x=y_{1}\)
  \(y_{1}=x_{1}-a/b*y_{1}\)
  通解\(x = x_{0}+(b/gcd)*t\)
  \(y=y_{0}-(a/gcd)*t\)

拓展欧几里得代码（放上代码和应用）

int exgcd(int a,int b,int &x,int &y)
{
    if(b == 0) { x = 1;y = 0;return a; }
    int temp = exgce(b,a%b,x,y);
    int t = x;x = y;y = t-a/b*y;
    return temp;
}

• 应用：
• 求解不定方程\(ax+by=c\)
• 求解线性同余方程
• 求解模的逆元

解不定式方程\(ax+by=c\)

将方程两遍同时除以\(gcd(a,b)\),设\(a' = a/gcd(a,b),b'=b/gcd(a,b),c'=c/gcd(a,b)\),则方程变形为a'x+b'y = c',因为a',b'互相质，所以\(gcd(a',b') = 1\)
由拓展欧几里得定理知一定的存在\(x_{0},y_{0}\)使得\(a'x_{0},b'y_{0}=1\)则可由\(exgcd\)求出\(x_{0},y_{0}\),将上式两边同时乘以\(gcd(a,b)\)得：
\(a'gcd(a,b)x_{0}+b'gcd(a,b)y_{0}=gcd(a,b) ==> ax_{0} + by_{0} = gcd(a,b) ==> ax_{0} + by_{0} = c/c'\),
所以方程的解\(x_{1} = x_{0} * c' = c/d*x_{0},y_{1} = y_{0} * c' = c/d * y_{0}\)为方程的一组解，则方程\(ax+bx=c\)的通解是
\(x = x_{1} + b/d*k = c/d*x_{0} + b/d*k\)
\(y = y_{1} - a/d*k = c/d*y_{0} - a/d*k\)

解模线性方程

• 对于线性同余方程：\(ax≡m(Mod b)\)转化为\(ax+by=m\)则可以直接求解
• \(a≡b(Mod c)\)成立的充要条件是\((a-b)=k*c\)
• \((ax-m) = by\)
• 如：\(5x≡2(Mod 3)\)转换为\(5x+3y=2\)
• \(d=1,x_{0}=-1,y_{0}=2\)
• 通解：\(x=-2+3t,y=4-5t\)

乘法逆元

• 存在\(x\)使得\(ax ≡ 1(mod p)\) 则称\(x\)是\(a\)关于\(p\)的乘法逆元
• 定理：\(a\)关于\(p\)的乘法逆元存在的充要条件是\(gcd(a,p) = 1\)
• 逆元有什么作用呢？
  当要求\((a/b)modp\)时,且\(a\)很大,我们就求\(b\)关于\(p\)的惩罚逆元\(x\),则有\((a/b)modp = (a*x)modp\)
• 证明：
  根据\(b*x≡1(mod p)\)有\(b*x=p*y+1\)
  则\(x=(p*y+1)/b\)
  把\(x\)代入\((a*x)modp\)得：
  \((a*(p*y+1)/b)mod p\)
  \(=((a*p*y)/b+a/b) mod p\)
  \(=[((a*p*y)/b)modp+(a/b)] modp\)
  \(=[(p*(a*y)/b) modp +(a/b)]mod p\)
  \(p*[(a*y)/b]mod p=0\)

求解逆元

• \(5x≡1(mod3)\)逆元为\(2\)
• \(ax≡1(modp)\)等价于\(ax+py=1\)
• 当\(gcd(a,p)!=1\)的时候是没有解的，这也是\(a*x+b*y=c\)有解的充要条件：\(c%gcd(a,b)==0\)
• 解有无数，如何求解最小正整数解？
• 用\(x_{0}%p\)就是最小解，为什么？
• 由通解知\(x = x_{0}+(p/gcd)*t\) 其中\(gcd=1\) 所以\(x=x_{0}+p*t\) 由于最小解为\((0,p)\)之间，所以\(x=x_{0}%p\)
• 如果\(x_{0}\)为负数，让\(x_{0}\)对\(abs(p)\),然后结果再加上\(abs(p)\)就行了

逆元例题

ZOJ 3609 Modular Inverse

观察归纳法 - 费马小定理

• 假设\(p\)是质数，且\(gcd(a,p)=1\),那么\(a^{p-1}≡1(mod p)\)即：假如\(a\)是整数，\(p\)是质数，且\(a、b\)互质，那么\(a\)的\((p-1)\)次方除以\(p\)的余数恒等于\(1\)
• 应用：
  如果对于任意满足\(1≤b<p\)的\(b\)下式都成立
  \(b^{p-1}≡1(modp)\)
  则\(p\)必定是一个质数
  其实我们不必验证那么多，据说验证一次错误的概率为\(1/4\),所以一般验证\(10\)个质数就可以了

快速幂

• 求解a^n%k
  直接上代码(二分)(\(logn\))

int mul(int x,int y,int k)
{
    int ans = 1;x = x % k;
    while(x)
    {
        if(x&1) ans = (ans * x) % k;
        x = (x * x) % k;
        x >>= 1;
    } return ans;
}

• 如果该算法乘法溢出 我们会用到慢速乘法（乘法改成加法的形式）

long long mul(long long x,long long y,long long k)
{
    long long ans = 0;
    for (long long i=y;i;i>>=1)
    {
        if(i & 1) ans = (ans + x) % k;
        x = (x + x) % k;
    } return ans % k;
}

long long mull(long long x,long long y,long long k)
{
    long long ans = 1;
    for (long long i=y;i;i>>=1)
    {
        if(i & 1) ans = mul(ans,x) % k;
        x = mul(x,x) % k;
    } return ans % k;
}

欧拉函数

• 对于正整数\(n\),欧拉函数是指少于或等于\(n\)的数中与\(n\)互质的数的数学

• 例如\(φ(8)=4\),因为\(1,3,5,7\)均和\(8\)互质

• 通式：
  \(φ(x)=x(1-1/p_{1})(1-1/p_{2})(1-1/p_{3})(1-1/p_{4})...(1-1/p_{n})\),其中\(p_{1},p_{2}...p_{n}\)为\(x\)的所有质因数，\(x\)是不为\(0\)的整数 \(φ(1)=1\)(唯一和\(1\)互质的数(\(≤1\))就是\(1\)本身(注意：每种质因子只有一个)比如\(12 = 2*2*3\)那么\(φ(12) = 12 * (1-1/2) * (1-1/3) = 4\)
  若\(n\)是质数\(p\)的\(k\)次幂,\(φ(n)=p^{k}-p^{k-1}=(p-1)p^{k-1}\),因为除了\(p\)的倍数外，其他数都跟\(n\)互质
  设\(n\)为正整数，以\(φ(n)\)表示不超过\(n\)且与\(n\)互素的正整数的个数，成为\(n\)的欧拉函数值，这里函数\(φ：N->N,n->φ(n)\)成为欧拉函数

• 与\(n\)互质的所有数的和\(sum=n*[φ(n)/2]\)

• 证明：容斥原理
  

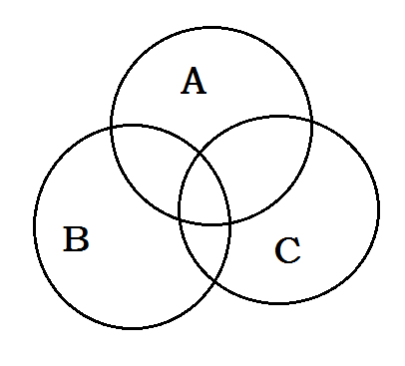
• \(A∪B∪C =A+B+C - A∩B - B∩C - C∩A + A∩B∩C\)

• 那么容斥的算法是:\(|U|\) - 不满足\(A_{1}\)的元素个数-不满足\(A_{2}\)的元素个数....+不满足\(A_{1}\)和\(A_{2}\)的元素个数+....-不满足\(A_{1}、A_{2}\)和\(A_{2}\)的元素个数-....

• \(<1001\)与\(1001\)互质的数一共有多少个？

• 分析：由于\(1001 = 7*11*13\),所以就是找不到被\(7,11,13\)整除的数

• 解答：\(1~1001\)中，有\(7\)的倍数\(1001/7=143(个)\) 有\(11\)的倍数\(1001/11 = 91\)(个),有\(13\)(个),有\(7*13=91\)的倍数\(1001/91 = 11\)(个),有\(11*13=143\)的倍数\(1001/143 = 7\)(个),有\(1001\)的倍数\(1\)个

• 由容斥原理知：在\(1~1001\)中，能被\(7\)或\(11\)或\(13\)整除的数有\((143+91+77) - (13+11+7) + 1 = 281\)(个),从而不能被\(7、11\)或\(13\)整除的数有\(1001-281=720\)(个),也就是说，小于\(1001\)与\(1001\)互质的数有\(720\)个

• \(p_{1},p_{2},p_{3}....p_{k}\)为\(n\)的质因子

• 与\(n\)不互质的数的个数为：
  \(n/p_{1}+n/p_{2}+...+n/p_{k}-n/(p_{1}*p_{2})-...-n/(pk-1*p_{k})-n/(p1*p2*p3)-...-n/(p_{k}-2*p_{k}-1*p_{k})-...+n/(p_{1}*p_{2}*...*p_{k})\)

• 所以与\(n\)互质的数的个数为：
  $φ(n)