2020杭电多校第一场 hdu6759 Leading Robots

题目链接

http://acm.hdu.edu.cn/showproblem.php?pid=6759

题目大意

有 N 个机器人赛跑 , 第 i 个机器人初始速度为0 , 加速度为ai , 位置为 bi

现在所有机器人将开始行动 , 问有多少个机器人可以任意时刻当上第一

解题思路 

以 0 点为初始点, 那么第 i 个机器人行动了 t 秒后的位置为 $S_{i}=\dfrac{1}{2}a_{i}t^{2}+b_{i}$

我们令 y = Si , x = 1/2t^2 , ki = ai , di = bi

那么第 i 个机器人的运行轨迹就可以转换为一元一次方程 yi = ki * x + di

如下图

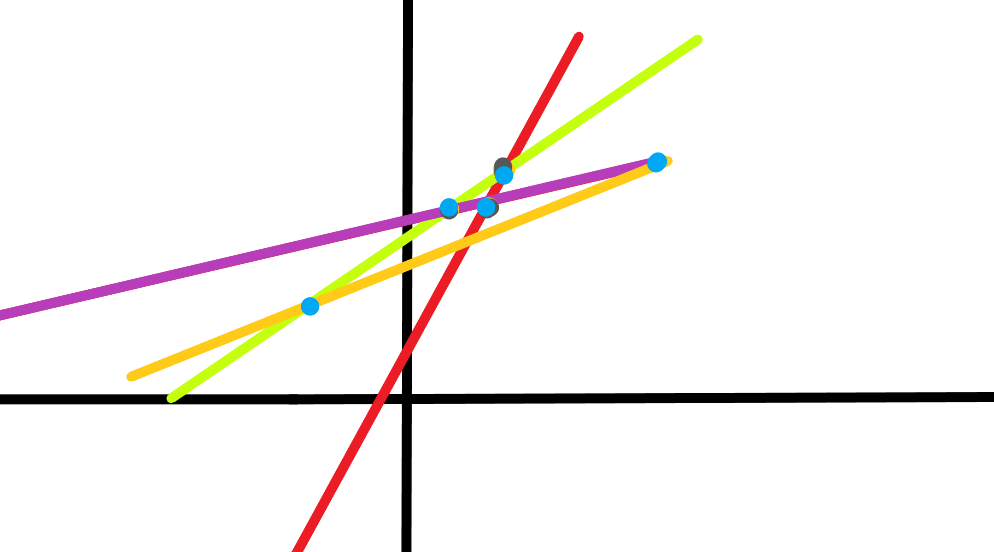
那么什么样的运动轨迹可以在某个时刻成为第一名的呢

不难发现 , 我们以二维的视角从上往下看 , 能看到的直线对应的机器人则有机会成为第一

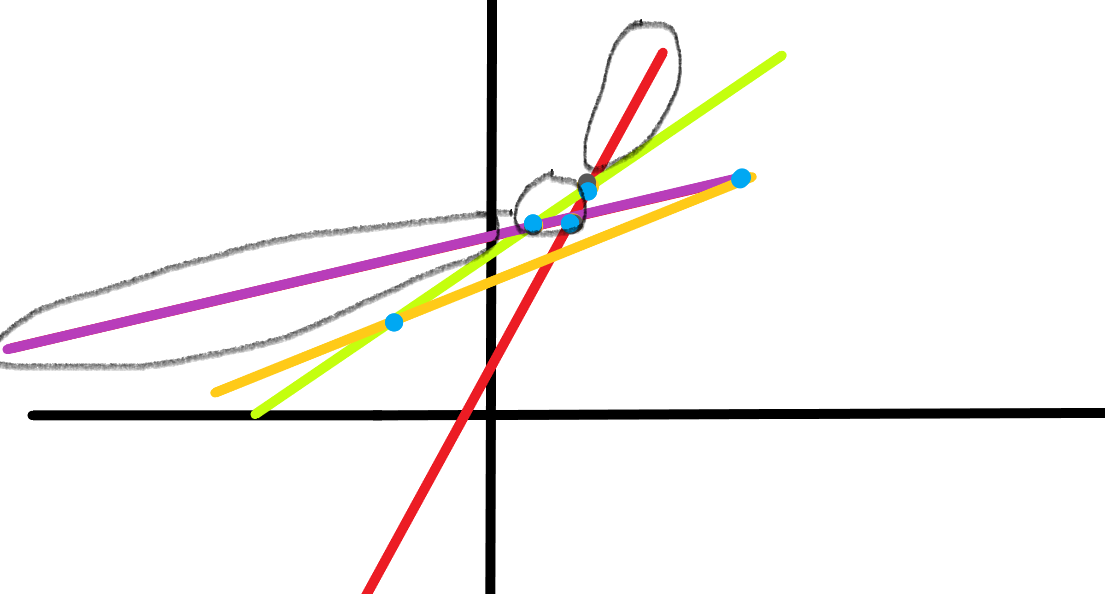
再仔细观察 , 又可发现↓

对于一条直线C, 若存在一条斜率比它大的直线A,和斜率比它小的直线B

且 AC 的交点在BC的横坐标上的左边(对应下图中)蓝点和绿点 , 则直线C就会被 “覆盖”

所以我们可以按照斜率从大到小排序 , 用单调栈维护

先将斜率最大的A入栈  , 然后将次大的C入栈 , 然后判断当前直线 AC 的交点是否会在 BC的左边

在则弹出 C 进行下轮判断 , 直到不在或者栈中只剩 A  

最后栈内剩余的元素则是可以从上帝视角可以看到的直线个数

当然题目还有些细节要处理 : 

①、上帝视角可以看到的直线可能是位于 X 的负半轴的 , 而 t^2 是大于等于 0 的

这种情况我们只要加入一条斜率为负数 , 经过原点的直线即可 ( 答案个数 = 最后栈的大小 - 1)

②、题目可能存在两条重合的直线 , 这种情况按题目的意思谁都不能成为唯一的第一

所以对于每条直线我们要判断一下它被是否有重合

update :

为了方便读者观看我在赛后优化了代码 , 减少了一部分不要的语句导致除了点小锅

至于读入读反了能过也是神奇 hh

其中为了处理细节①所加入的直线应该满足的条件为

①、斜率为负数

②、截距取其它直线截距的max(要覆盖掉其它直线的负半段)

感谢 @AKDA 提出的问题 , 感谢@Overstars给出的hack数据

AC_Code

#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
#define rep(i,a,n) for (int i=a;i<=n;i++)
#define per(i,n,a) for (int i=n;i>=a;i--)
#define int long long
using namespace std;
#define ld long double
const int N = 5e5 + 10;
const ld eps=1e-20;
struct node
{
    ld k , b;
    int id , w;
} li[N];
int sta[N << 1] , top;
bool cmp(node t1 , node t2)
{
    if(t1.k == t2.k) return t1.b > t2.b;
    return t1.k > t2.k;
}
ld get(int x,int y)
{
    return (li[x].b - li[y].b) / (li[y].k - li[x].k);
}
map<pair<int , int> , int>mp;
signed main()
{
    ios::sync_with_stdio(false) , cin.tie(0) , cout.tie(0);
    int t;
    cin >> t;
    while(t --)
    {
        mp.clear();
        int n ;
        cin >> n;
        int cnt = 0 , ans = 0 , ma = -1;
        rep(i , 1 , n)
        {
            int k , b;
            cin >> b >> k;
            ma = max(ma , b);
            pair<int , int> now = make_pair(k , b);
            if(!mp[now])
            {
                mp[now] = ++ cnt;
                li[cnt].k = k , li[cnt].b = b;
                li[cnt].id = cnt , li[cnt].w = 1;
            }
            else li[mp[now]].w ++;
        }
        n ++;
        li[n].k = -1 , li[n].b = ma , li[n].w = 0;
        sort(li + 1 , li + 1 + n , cmp);
        sta[1] = 1 , top = 2;
        rep(i , 2 , n)
        {
            if(li[i].k == li[i - 1].k) continue ;
            while(top >= 3 && get(sta[top - 1] , sta[top - 2]) - get(sta[top - 1] , i) <= eps) top --;
            sta[top ++] = i;
        }
        rep(i , 1 , top - 1) if(li[sta[i]].w < 2) ans ++ ;
        cout << ans - 1 << '\n';
        rep(i , 1 , n) li[i].k = li[i].b = li[i].id = li[i].w = 0;
    }
    return 0;
}