Hall定理和匈牙利算法（匹配与覆盖，因子分解）

Hall定理：

设G为具有二分类（X,Y）的偶图，则G包含饱和点X的每个顶点的匹配当且仅当|N(S)|>=|S|，对所有S是X的子集都成立。

发现上面这句话读的很拗口，虽然是课本原话，这里我引用wiki。hall定理全名hall marriage theorem.他在图论和组合数学中都存在，这里我们只指出他在图论中的作用定义。

　　作用：

　　The graph theoretic formulation deals with a bipartite graph. It gives a necessary and sufficient condition for finding a matching that covers at least one side of the graph.

　　在图论中，Hall定理涉及到了二部图。他指出包含至少一边（X或y）所有顶点的匹配（X或Y至少一边的全部点集为饱和点）的充要条件。也表示最大匹配数=Min(|X|,|Y|)。注：个人感觉这里的covers表达的是饱和点的意思，

　　定义：

 Let G be a finite bipartite graph with bipartite sets X and Y ( G:= (X + Y, E)). For a set W of vertices in X, let {\displaystyle N_{G}(W)} denote the neighborhood of W in G, i.e. the set of all vertices in Y adjacent to some element of W. The marriage theorem in this formulation states that there is a matching that entirely covers X if and only if for every subset W of X:

 

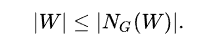
In other words: every subset W of X has sufficiently many adjacent vertices in Y.

A generalization to general graphs (that are not necessarily bipartite) is provided by the Tutte theorem.

　　定义大意是，存在二部图XY，W是点集X的一个子集。则邻集N(W)显然是Y的子集，Hall定理表明X点集子集W是饱和点子集（W中每个点都属于最大匹配），当且仅当对于每一个子集W，都有子集W小于邻集N（W）。

换句话说，X的每个子点集W都有足够多的邻集点在Y中。

Tutte定理是Hall定理的一般化定理。

翻译的不好，看不懂中文 还是看一下英语吧。

证明是用的匈牙利算法，这个算法也是寻找偶图最大匹配的好算法。

匈牙利算法：https://blog.csdn.net/cillyb/article/details/55511666