LeetCode题解-06(分治、动态规划)
目录
LeetCode题解
chap-15:分治#
1、不同的二叉搜索树 II【卡特兰数】#
class Solution {
public:
vector<TreeNode*> generateTrees(int n) {
return dfs(1,n);
}
vector<TreeNode*> dfs(int l,int r){
if(l>r) return{nullptr};
vector<TreeNode*> res;
for(int i = l;i<=r;i++){
auto left = dfs(l,i-1),right = dfs(i+1,r);
for(auto &l:left){
for(auto &r:right){
auto root = new TreeNode(i);
root->left = l;
root->right = r;
res.push_back(root);
}
}
}
return res;
}
};
2、为运算表达式设计优先级#
class Solution {
public:
vector<int> diffWaysToCompute(string ep) {
vector<int> ans;
for(int i=0;i<ep.size();i++){
if(ep[i]<'0'){
for(auto &a:diffWaysToCompute(ep.substr(0,i)))
for(auto &b:diffWaysToCompute(ep.substr(i+1)))
ans.push_back(ep[i]=='+'?a+b:ep[i]=='-'?a-b:a*b);
}
}
return ans.empty()?vector<int>{stoi(ep)}:ans;
}
};
3、从前序与中序遍历序列构造二叉树#
class Solution {
public:
unordered_map<int,int> hash;
TreeNode* buildTree(vector<int>& pre, vector<int>& in) {
for(int i=0;i<pre.size();i++) hash[in[i]]=i;
return dfs(pre,in,0,pre.size()-1,0,in.size()-1);
}
TreeNode* dfs(vector<int>&pre, vector<int>&in, int pl,int pr,int il,int ir){
if(pl>pr) return nullptr;
auto root = new TreeNode(pre[pl]);
int i = hash[root->val];
root->left = dfs(pre,in,pl+1,i-il+pl,il,i-1);
root->right = dfs(pre,in,i-il+pl+1,pr,i+1,ir);
return root;
}
};
4、从中序与后序遍历序列构造二叉树#
class Solution {
public:
unordered_map<int, int> pos;
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
for (int i = 0; i < inorder.size(); i ++ ) pos[inorder[i]] = i;
return build(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);
}
TreeNode* build(vector<int>& inorder, vector<int>& postorder, int il, int ir, int pl, int pr) {
if (il > ir) return NULL;
auto root = new TreeNode(postorder[pr]);
int k = pos[root->val];
root->left = build(inorder, postorder, il, k - 1, pl, pl + k - 1 - il);
root->right = build(inorder, postorder, k + 1, ir, pl + k - 1 - il + 1, pr - 1);
return root;
}
};
5、将有序数组转换为二叉搜索树#
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return dfs(0,nums.size()-1,nums);
}
TreeNode* dfs(int l, int r, vector<int>&nums){
if(l>r) return nullptr;
int mid=l+r>>1;
auto root = new TreeNode(nums[mid]);
root->left = dfs(l,mid-1,nums);
root->right = dfs(mid+1,r,nums);
return root;
}
};
6、有序链表转换二叉搜索树#
class Solution {
public:
TreeNode* sortedListToBST(ListNode* head) {
if(head == nullptr) return nullptr;
int n=0;
for(auto p = head;p;p = p->next) n++;
if(n == 1) return new TreeNode(head->val);
auto cur = head;
for(int i =0;i<n/2-1;i++){
cur = cur->next;
}
auto t = new TreeNode(cur->next->val);
t->right = sortedListToBST(cur->next->next);
cur->next = nullptr;
t->left = sortedListToBST(head);
return t;
}
};
[Go Back~](# LeetCode题解)
chap-16:动态规划#
section16-1: 背包问题#
1、01背包 分割等和子集#
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum=accumulate(nums.begin(),nums.end(),0);
if(sum%2) return false;
sum/=2; vector<bool>f(sum+1,false); f[0]=true;
for(auto &n:nums){
for(int i=sum;i>=n;i--)
f[i] = f[i]|f[i-n];
if(f[sum]) return true;
}
return f[sum];
}
};
2、01背包 目标和 【×】#
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int offset=accumulate(nums.begin(),nums.end(),0);
offset = max(abs(target), offset);
int n=nums.size();
vector<vector<int>> f(n+1,vector<int>(2*offset+1,0));
f[0][offset+0]=1;
for(int i=1;i<=n;i++){
for(int j=offset;j>=-offset;j--){
if(j-nums[i-1]>=-offset)
f[i][j+offset] += f[i-1][j-nums[i-1]+offset] ;
if(j+nums[i-1]<=offset)
f[i][j+offset] += f[i-1][j+nums[i-1]+offset] ;
}
}
return f[n][target+offset];
}
};
3、完全背包 完全平方数#
class Solution {
public:
int numSquares(int n) {
vector<int> f(n+1,INT_MAX); f[0]=0;
for(int i=1;i*i<=n;i++){
int t = i*i;
for(int j=t;j<=n;j++)
f[j] = min(f[j], f[j-t]+1);
}
return f[n];
}
};
4、完全背包 零钱兑换#
class Solution {
public:
int coinChange(vector<int>& coins, int m) {
int n = coins.size();
sort(coins.begin(),coins.end());
vector<int> f(m+1,0x3f3f3f3f);
f[0] = 0;
for(int i = 1;i<=m;i++){
for(int j = n-1;j>=0;j--){
if(i - coins[j] >= 0)
f[i] = min(f[i - coins[j]] + 1,f[i]);
}
}
return f[m] == 0x3f3f3f3f ? -1 : f[m];
}
};
5、完全背包 零钱兑换 II#
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int> f(amount+1,0);
f[0]=1;
for(auto &coin : coins){
for(int i=coin;i<=amount;i++)
f[i] += f[i-coin];
}
return f[amount];
}
};
6、二维背包 一和零#
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<vector<int>>f(m+1,vector<int>(n+1,0));
for(auto &s:strs){
int cnt0=0,cnt1=0;
for(auto &c:s) if(c=='0') cnt0++; else cnt1++;
for(int i=m;i>=cnt0;i--)
for(int j=n;j>=cnt1;j--)
f[i][j] = max(f[i][j], f[i-cnt0][j-cnt1]+1);
}
return f[m][n];
}
};
7、求方案数 数位成本和为目标值的最大数字#
class Solution {
public:
string largestNumber(vector<int>& cost, int target) {
vector<int> f(target+1,INT_MIN);
f[0]=0;
for(int i=0;i<cost.size();i++)
for(int j=cost[i];j<=target;j++)
f[j] = max(f[j], f[j-cost[i]]+1);
if(f[target]<0) return "0";
string ans;
for (int i = 8, j = target; i >= 0; i--) {
while (j >= cost[i] && f[j] == f[j - cost[i]] + 1) {
ans += to_string(i + 1);
j -= cost[i];
}
}
return ans;
}
};
[Go Back~](# LeetCode题解)
section16-2: LIS模型#
1、最长递增子序列#
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> dp(nums.size(),1); // O(n^2)
int res = 1;
for(int i= 1;i<nums.size();i++){
for(int j = 0;j<i;j++){
if(nums[i]>nums[j])
dp[i] = max(dp[i],dp[j]+1);
}
res = max(dp[i], res);
}
return res;
}
};
// O(nlog(n))
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n=nums.size(), len=1;
vector<int> f(n+1,0);
f[len]=nums[0];
for(int i=1;i<=n;i++){
int l=1, r=len;
while(l<=r){
int mid=l+r>>1;
if(f[mid] < nums[i-1]) l = mid+1;
else r=mid-1;
}
if(l>len) len++; f[l]=nums[i-1];
}
return len;
}
};
2、俄罗斯套娃信封问题#
class Solution {
public:
int maxEnvelopes(vector<vector<int>>& envelopes) {
int n = envelopes.size();
sort(envelopes.begin(),envelopes.end());
vector<int> f(n+1,1);
int ans=0;
for(int i=1;i<=n;i++){
int w=envelopes[i-1][0], h=envelopes[i-1][1];
for(int j=1;j<i;j++){
if(envelopes[j-1][0]<w && envelopes[j-1][1]<h)
f[i] = max(f[i], f[j]+1);
}
ans = max(ans,f[i]);
}
return ans;
}
};
3、最大整除子集#
class Solution {
public:
vector<int> largestDivisibleSubset(vector<int>& nums) {
sort(nums.begin(), nums.end());
vector<int> f(nums.size()+1,0);
int t=0;
for(int i=1;i<=nums.size();i++){
f[i]=1;
for(int j=1;j<i;j++)
if(nums[i-1]%nums[j-1] == 0)
f[i] = max(f[i],f[j]+1);
t=max(t,f[i]);
}
vector<int> ans;
for(int j=nums.size();j>=1;j--){
if(t == f[j]){
if(ans.empty()) t--,ans.push_back(nums[j-1]);
else if(ans.back() % nums[j-1] == 0)
t--,ans.push_back(nums[j-1]);
}
}
return ans;
}
};
4、无矛盾的最佳球队#
class Solution {
public:
int bestTeamScore(vector<int>& scores, vector<int>& ages) {
int n=scores.size(); vector<int> rank(n);
for(int i=0;i<n;i++) rank[i]=i;
sort(rank.begin(), rank.end(), [&](int &i, int &j){
if(scores[i]!=scores[j]) return scores[i]<scores[j];
else return ages[i]<ages[j];
});
vector<int> f(n+1); int ans=0;
for (int i = 0; i < n; i++) {
f[i] = scores[rank[i]];
for (int j = 0; j < i; j++)
if (ages[rank[j]] <= ages[rank[i]])
f[i] = max(f[i], f[j] + scores[rank[i]]);
ans = max(ans, f[i]);
}
return ans;
}
};
5、堆叠长方体的最大高度#
class Solution {
public:
int maxHeight(vector<vector<int>>& cuboids) {
for(auto &cuboid:cuboids){
sort(cuboid.begin(),cuboid.end());
}
sort(cuboids.begin(),cuboids.end());
vector<int> f(cuboids.size(),0);
int ans=0;
for(int i=0;i<cuboids.size();i++){
f[i]=cuboids[i][2];
for(int j=0;j<i;j++)
if(cuboids[j][1]<=cuboids[i][1] && cuboids[j][2]<=cuboids[i][2])
f[i] = max(f[i],f[j]+cuboids[i][2]);
ans=max(ans,f[i]);
}
return ans;
}
};
[Go Back~](# LeetCode题解)
section16-3: 线性DP#
1、最大子数组和#
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int sum = 0,ans = -0x3f3f3f3f;
for(auto &item:nums){
sum += item;
ans = max(sum,ans);
if(sum < 0) sum = 0;
}
return ans;
}
};
2、不同路径#
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> f(n+1,0);
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++){
if(i==1&&j==1) f[j]=1;
else f[j] = f[j] + f[j-1];
}
return f[n];
}
};
3、不同路径 II#
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& w) {
int n=w.size(), m=w[0].size();
if(w[0][0] || w[n-1][m-1]) return 0;
vector<vector<int>> f(n+1,vector<int>(m+1,0));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(i==1 && j==1) f[i][j]=1;
else if(!w[i-1][j-1]) f[i][j]=f[i-1][j]+f[i][j-1];
return f[n][m];
}
};
4、最小路径和#
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int n=grid.size(), m=grid[0].size();
vector<int>f(m+1,0x3f3f3f3f);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
if(i==1 && j==1) f[j]=grid[i-1][j-1];
else f[j] = min(f[j], f[j-1]) + grid[i-1][j-1];
}
return f[m];
}
};
5、爬楼梯#
class Solution {
public:
int climbStairs(int n) {
vector<int> f(n+1); f[0]=1, f[1]=1;
for(int i=2;i<=n;i++)
f[i] = f[i-1]+f[i-2];
return f[n];
}
};
class Solution {
public:
int climbStairs(int n) {
int a=1, b=1, c;
for(int i=2;i<=n;i++){
c = a+b; a = b; b = c;
}
return b;
}
};
6、编辑距离 【×】#
class Solution {
public:
int minDistance(string word1, string word2) {
int n=word1.size(), m=word2.size();
word1 = ' '+word1;
word2 = ' '+word2;
vector<vector<int>> f(n+1,vector<int>(m+1,0x3f3f3f));
for (int i = 0; i <= n; i ++ ) f[i][0] = i;
for (int i = 1; i <= m; i ++ ) f[0][i] = i;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(word2[j] == word1[i])
f[i][j] = min(f[i-1][j-1], f[i][j]);
else
f[i][j] = min(f[i-1][j-1]+1, min(f[i-1][j]+1, f[i][j-1]+1));
}
}
return f[n][m];
}
};
7、解码方法#
class Solution {
public:
int numDecodings(string s) {
int n=s.size();
vector<int> f(n+1,0);
s = ' '+s;
f[0]=1;
for(int i=1;i<=n;i++){
if(i==1) {if(s[i] != '0') f[i]=1;}
else {
string t; t+=s[i-1]; t+=s[i];
int a = stoi(t);
if(s[i] != '0'){
f[i] = f[i-1];
if(a>=10 && a<=26) f[i] = f[i]+f[i-2];
}else{
if(a == 10 || a == 20)
f[i] = f[i-2];
}
}
}
return f[n];
}
};
8、不同的二叉搜索树#
class Solution {
public:
int numTrees(int n) {
vector<int>f(n+1,0);
f[0]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
f[i] += f[i-j]*f[j-1];
return f[n];
}
};
9、交错字符串#
class Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int n1 = s1.size(), n2 = s2.size(), n = s3.size();
if((n1+n2) != n) return false;
vector<vector<bool>> f(n1+1,vector<bool>(n2+1, false));
s1 = ' '+s1; s2 = ' '+s2; s3 = ' '+s3;
for(int j=0;j<=n1;j++)
for(int i=0;i<=n2;i++){
if(!i && !j) f[j][i] = 1;
else{
if(j && s1[j] == s3[i+j]) f[j][i] = f[j-1][i];
if(i && s2[i] == s3[i+j]) f[j][i] = f[j][i] || f[j][i-1];
}
}
return f[n1][n2];
}
};
10、不同的子序列#
class Solution {
public:
int numDistinct(string s, string t) {
int n=s.size(),m=t.size();
s = ' '+s; t = ' '+t;
vector<vector<unsigned long long>>f(m+1,vector<unsigned long long>(n+1,0));
for(int i=0;i<=n;i++) f[0][i]=1;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++){
if(s[j] != t[i]) f[i][j] = f[i][j-1];
else f[i][j] = f[i-1][j-1]+f[i][j-1];
}
return f[m][n];
}
};
11、杨辉三角#
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> ans;
for(int i=1;i<=numRows;i++){
if(ans.empty()) ans.push_back({1});
else{
vector<int> t; t.push_back(1);
for(int j=2;j<=i;j++){
if(j>ans.back().size()) t.push_back(1);
else{
t.push_back(ans.back()[j-2]+ans.back()[j-1]);
}
}
ans.push_back(t);
}
}
return ans;
}
};
12、杨辉三角 II#
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> ans(rowIndex+1,0);
for(int i=0;i<=rowIndex;i++){
for(int j=i;j>=0;j--){
if(!j) ans[j] = 1;
else{
if(j < i) ans[j] = ans[j-1] + ans[j];
else ans[j] = ans[j-1] + 0;
}
}
}
return ans;
}
};
13、三角形最小路径和#
class Solution {
public:
int minimumTotal(vector<vector<int>>& dp) {
for(int i = dp.size() - 2;i>=0;i--){
for(int j = 0;j<dp[i].size();j++){
dp[i][j] += min(dp[i+1][j],dp[i+1][j+1]);
}
}
return dp[0][0];
}
};
14、分割回文串#
class Solution {
public:
vector<vector<bool>> f;
vector<vector<string>> res;
vector<vector<string>> partition(string s) {
int n=s.size();
f = vector<vector<bool>>(n,vector<bool>(n,false));
f[0][0]=1;
for(int i=1;i<n;i++){
f[i][i]=1;
if(s[i-1] == s[i]) f[i-1][i]=1;
}
for(int len=2;len<n;len++)
for(int i=0;i+len<n;i++){
f[i][i+len] = f[i+1][i+len-1] && (s[i]==s[i+len]);
}
vector<string> path;
dfs(s,0,path);
return res;
}
void dfs(string&s, int u,vector<string> path){
if(u == s.size()) res.push_back(path);
else{
for(int i=u;i<s.size();i++){
if(f[u][i]){
path.push_back(s.substr(u,i-u+1));
dfs(s,i+1,path);
path.pop_back();
}
}
}
}
};
15、分割回文串 II【×】#
class Solution {
public:
int minCut(string s) {
int n = s.size();
vector<vector<bool>>f(n,vector<bool>(n,false));
f[0][0]=1;
for(int i=1;i<n;i++){
f[i][i]=1, f[i-1][i]=(s[i-1]==s[i]);
}
for(int len=2;len<n;len++){
for(int j=0;j+len<n;j++)
f[j][j+len] = f[j+1][j+len-1] && (s[j] == s[len+j]);
}
vector<int> dp(n+1,INT_MAX);
dp[0]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<i;j++)
if(f[j][i-1]) dp[i] = min(dp[i], dp[j]+1);
}
return max(0,dp[n]-1);
}
};
16、地下城游戏【×】#
class Solution {
public:
int calculateMinimumHP(vector<vector<int>>& dungeon) {
int n=dungeon.size(), m=dungeon[0].size();
vector<vector<int>> f(n+1,vector<int>(m+1,0x3f3f3f));
f[n][m-1]=1, f[n-1][m]=1;
for(int i=n-1;i>=0;i--){
for(int j=m-1;j>=0;j--){
f[i][j] = max(1,min(f[i+1][j],f[i][j+1])-dungeon[i][j]);
}
}
return f[0][0];
}
};
17、最大正方形#
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int n = matrix.size(), m = matrix[0].size();
vector<vector<int>> f(n+1,vector<int>(m+1));
int res = 0;
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
if(matrix[i-1][j-1] == '0') f[i][j] = 0;
else{
f[i][j] = min(f[i-1][j-1],min(f[i-1][j],f[i][j-1])) + 1;
res = max(res,f[i][j]);
}
}
}
return res * res;
}
};
18、摆动序列#
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
int n=nums.size();
vector<int> f1(n,0); //上升序列
vector<int> f0(n,0); //下沉序列
f0[0]=f1[0]=1;
for(int i=1;i<n;i++){
if(nums[i]>nums[i-1]){
f1[i]=f0[i-1]+1;
f0[i]=f0[i-1];
}else if(nums[i]<nums[i-1]){
f0[i]=f1[i-1]+1;
f1[i]=f1[i-1];
}else f0[i]=f0[i-1], f1[i]=f1[i-1];
}
return max(f0[n-1],f1[n-1]);
}
};
19、斐波那契数#
class Solution {
public:
int fib(int n) {
if(!n) return 0;
vector<int> f(n+1,0);
f[0]=0, f[1]=1;
for(int i=2;i<=n;i++) f[i]=f[i-1]+f[i-2];
return f[n];
}
};
class Solution {
public:
int fib(int n) {
if(!n) return 0;
int c=0, a=0, b=1;
for(int i=2;i<=n;i++) {
c=a+b;
a = b;
b = c;
}
return b;
}
};
20、自由之路【×】#
class Solution {
public:
int findRotateSteps(string ring, string key) {
int n=ring.size(), m=key.size();
vector<vector<int>> f(m,vector<int>(n,0x3f3f3f));
for(int i=0;i<n;i++){
if(ring[i] == key[0])
f[0][i] = min(i,n-i)+1;
}
for(int i=1;i<m;i++){
for(int j=0;j<n;j++){
if(key[i] == ring[j]){
for(int k=0;k<n;k++){
if(key[i-1] == ring[k]){
int cost = f[i-1][k] + min((j-k+n)%n, (k-j+n)%n) +1;
f[i][j] = min(f[i][j], cost);
}
}
}
}
}
int ans=INT_MAX;
for(int i=0;i<n;i++) ans=min(ans, f[m-1][i]);
return ans;
}
};
21、掷骰子的N种方法#
class Solution {
public:
int numRollsToTarget(int n, int k, int target) {
const int mod = 1e9 + 7;
vector<vector<int>>f(n+1,vector<int>(target+1,0));
f[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=k;j++){
for(int t=j;t<=target;t++)
f[i][t] = (f[i][t] + f[i-1][t-j])%mod;
}
}
return f[n][target];
}
};
22、带限制的子序列和 【单调队列】#
class Solution {
public:
int constrainedSubsetSum(vector<int>& nums, int k) {
int n=nums.size();
vector<int> f(n,0);
f[0]=nums[0];
int ans=nums[0];
deque<int> q;
q.push_back(0);
for(int i=1;i<n;i++){
while(q.size() && i-q.front()>k) q.pop_front();
f[i] = max(0, f[q.front()]) + nums[i];
ans = max(f[i], ans);
while(q.size() && f[i] >= f[q.back()]) q.pop_back();
q.push_back(i);
}
return ans;
}
};
23、跳跃游戏 VI#
class Solution {
public:
int maxResult(vector<int>& nums, int k) {
int n=nums.size();
vector<int> f(n,0); f[0]=nums[0];
deque<int> q; q.push_back(0);
for(int i=1;i<n;i++){
while(q.size() && i - q.front()>k) q.pop_front();
f[i] = f[q.front()] + nums[i];
while(q.size() && f[i] >= f[q.back()]) q.pop_back();
q.push_back(i);
}
return f[n-1];
}
};
[Go Back~](# LeetCode题解)
section16-4: 杂选热点DP问题#
1、打家劫舍#
class Solution {
public:
int rob(vector<int>& nums) {
int n=nums.size();
vector<int> f(n+1,0);
for(int i=1;i<=n;i++){
if(i==1) f[i] = max(f[i-1], nums[i-1]);
else f[i] = max(f[i-1], f[i-2]+nums[i-1]);
}
return f[n];
}
};
2、打家劫舍 II#
class Solution {
public:
int rob(vector<int>& nums) {
int n=nums.size(), ans=0;
vector<int> f(n+1,0);
for(int i=n-1;i>=0;i--){
// 第一个不取,最后一个取
if(i==n-1) f[i] = nums[i];
else if(i == 0) f[i] = f[i+1];
else f[i] = max(f[i+1], f[i+2]+nums[i]);
}
ans = max(ans, f[0]);
f = vector<int>(n+1,0);
for(int i=1;i<=n;i++){
// 第一个取,最后一个不取
if(i==1) f[i] = nums[i-1];
else if(i == n) f[i] = f[i-1];
else f[i] = max(f[i-1], f[i-2]+nums[i-1]);
}
ans = max(ans,f[n]);
return ans;
}
};
3、摘樱桃 【×】#
class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int n=grid.size();
vector<vector<vector<int>>> f(2*n,vector<vector<int>>(n,vector<int>(n,-0x3f3f3f)));
f[0][0][0] = grid[0][0];
for(int k=1;k<=2*n-2;k++){
for(int i1=0;i1<n;i1++){
for(int i2=0;i2<n;i2++){
int j1 = k-i1, j2 = k-i2;
if (j1 < 0 || j1 >= n || j2 < 0 || j2 >= n) continue; //越界
if(grid[i1][j1]==-1 || grid[i2][j2] == -1) continue;
int t = grid[i1][j1]; //取得该格子
if (i1 != i2) t += grid[i2][j2]; //没有重合
int &x = f[k][i1][i2];
x = max(x, f[k - 1][i1][i2] + t);
if(i1) x = max(x, f[k-1][i1-1][i2] + t);
if(i2) x = max(x, f[k-1][i1][i2-1] + t);
if(i1 && i2) x = max(x, f[k-1][i1-1][i2-1] + t);
}
}
}
return max(0,f[2*n-2][n-1][n-1]);
}
};
4、摘樱桃 II 【数字三角形dp】#
class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<vector<int>>> f(n, vector<vector<int>> (m, vector<int> (m, -1)));
f[0][0][m - 1] = grid[0][0] + grid[0][m - 1]; //开始状态
int res = 0;
for (int k = 1; k < n; k ++) //从第二行开始循环
for (int i = 0; i < m; i ++)
for (int j = 0; j < m; j ++)
for (int a = i - 1; a <= i + 1; a ++) // 可能情况枚举
for (int b = j - 1; b <= j + 1; b ++)
{
if (a < 0 || a >= m || b < 0 || b >= m) continue; //越界
int t = f[k - 1][a][b];
if (t < 0) continue; //不合法
if (i == j) f[k][i][j] = max(f[k][i][j], t + grid[k][i]); //重合时只算一次分值
else f[k][i][j] = max(f[k][i][j], t + grid[k][i] + grid[k][j]);
res = max(res, f[k][i][j]);
}
return res;
}
};
5、买卖股票的最佳时机 【贪心】#
class Solution {
public:
int maxProfit(vector<int>& prices) {
int minp = prices[0], ans = 0;
for(int i=1;i<prices.size();i++){
if(prices[i] <= minp)
minp = prices[i];
else
ans = max(ans,prices[i] - minp);
}
return ans;
}
};
6、买卖股票的最佳时机 II 【状态机】#
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n=prices.size();
int f[n][2]; f[0][0] = 0, f[0][1] = -prices[0];
for(int i=1;i<n;i++){
f[i][0] = max(f[i-1][0], f[i-1][1]+prices[i]);
f[i][1] = max(f[i-1][1], f[i-1][0]-prices[i]);
}
return f[n-1][0];
}
};
// 空间优化
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n=prices.size(), f = 0, g = -prices[0];
for(int i=1;i<n;i++){
int last_f = f, last_g = g;
f = max(last_f, last_g+prices[i]);
g = max(last_g, last_f-prices[i]);
}
return f;
}
};
7、买卖股票的最佳时机 III#
// 状态机
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n=prices.size(); int f[3][n+1][2];
memset(f,-0x3f,sizeof f);
for(int i=0;i<=n;i++) f[0][i][0] = 0;
for(int j=1;j<=n;j++){
for(int i=1;i<=2;i++){
f[i][j][0] = max(f[i][j-1][0], f[i][j-1][1]+prices[j-1]);
f[i][j][1] = max(f[i][j-1][1], f[i-1][j-1][0]-prices[j-1]);
}
}
int ans=0;
for(int k=0;k<=2;k++) ans = max(ans, f[k][n][0]);
return ans;
}
};
// 前后缀分解
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n=prices.size(); int f[n], g[n];
memset(f,0,sizeof f); memset(g,0,sizeof g);
for(int i=1,minp=prices[0];i<n;i++){
minp = min(minp, prices[i]);
f[i] = max(f[i-1], prices[i]-minp);
}
for(int i=n-2,maxp=prices[n-1];i>=0;i--){
maxp = max(maxp, prices[i]);
g[i] = max(g[i+1], maxp-prices[i]);
}
int ans=0;
for(int i=0;i<n;i++) ans = max(ans, f[i]+g[i]);
return ans;
}
};
8、买卖股票的最佳时机 IV 【状态机】#
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
int n=prices.size(); int f[k+1][n+1][2];
memset(f,-0x3f,sizeof f);
for(int i=0;i<=n;i++) f[0][i][0] = 0;
for(int j=1;j<=n;j++){
for(int i=1;i<=k;i++){
f[i][j][0] = max(f[i][j-1][0], f[i][j-1][1]+prices[j-1]);
f[i][j][1] = max(f[i][j-1][1], f[i-1][j-1][0]-prices[j-1]);
}
}
int ans=0;
for(int t=0;t<=k;t++) ans = max(ans, f[t][n][0]);
return ans;
}
};
9、最佳买卖股票时机含冷冻期【状态机】#
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n=prices.size();
vector<int> f(n,0), g(n,0);// f为卖出状态, g为买入状态
f[0] = 0, g[0]=-prices[0];
for(int i=1;i<n;i++){
f[i] = max(f[i-1], g[i-1]+prices[i]);
if(i!=1) g[i] = max(f[i-2]-prices[i], g[i-1]);
else g[i] = max(g[i-1], -prices[i]);
}
return f[n-1];
}
};
10、买卖股票的最佳时机含手续费【状态机】#
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n=prices.size();
vector<int> f(n,0), g(n,0);
f[0]=0, g[0]=-prices[0];
for(int i=1;i<n;i++){
f[i] = max(f[i-1], g[i-1]+prices[i]-fee);
g[i] = max(g[i-1], f[i-1]-prices[i]);
}
return f[n-1];
}
};
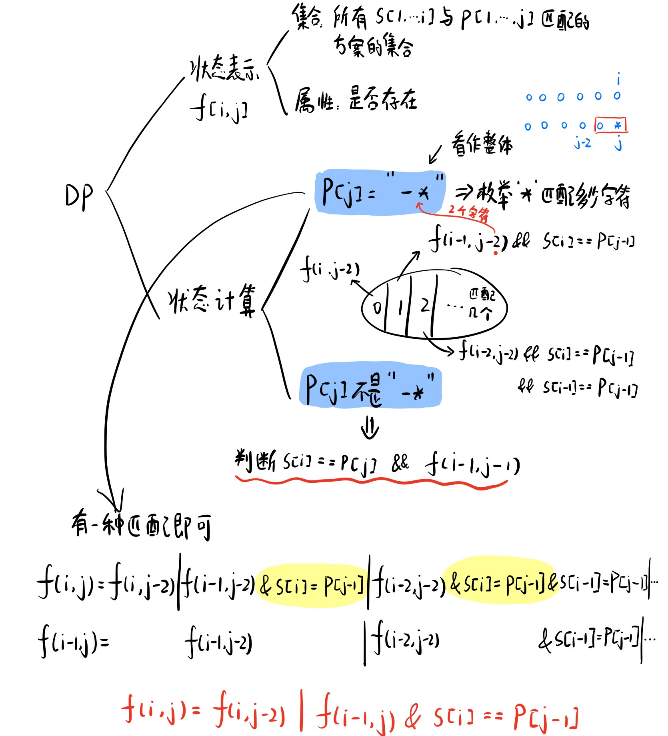
11、正则表达式匹配 【×】#
class Solution {
public:
bool isMatch(string s, string p) {
int n=s.size(), m=p.size();
s = ' '+s, p = ' '+p;
vector<vector<bool>> f(n+1,vector<bool>(m+1,false));
f[0][0]=true;
for(int i=0;i<=n;i++){
for(int j=1;j<=m;j++){
if(j+1<=m && p[j+1] == '*')continue;
if(p[j] == '*'){
f[i][j] = f[i][j-2] || i && f[i - 1][j] && (s[i] == p[j - 1] || p[j - 1] == '.');
}else if(i && p[j] != '*')
f[i][j] = f[i-1][j-1] && (s[i]==p[j] || p[j]=='.');
}
}
return f[n][m];
}
};
12、通配符匹配#
class Solution {
public:
bool isMatch(string s, string p) {
int n=s.size(), m=p.size();
s = ' '+s, p = ' '+p;
vector<vector<bool>> f(n+1,vector<bool>(m+1,false));
f[0][0]=true;
for(int i=0;i<=n;i++){
for(int j=1;j<=m;j++){
if(p[j]=='*') f[i][j] = f[i][j-1] || i && f[i-1][j];
else f[i][j] = i && (s[i]==p[j] || p[j]=='?') && f[i-1][j-1];
}
}
return f[n][m];
}
};
[Go Back~](# LeetCode题解)
23、跳跃游戏 VI#
class Solution {
public:
int maxResult(vector<int>& nums, int k) {
int n=nums.size();
vector<int> f(n,0); f[0]=nums[0];
deque<int> q; q.push_back(0);
for(int i=1;i<n;i++){
while(q.size() && i - q.front()>k) q.pop_front();
f[i] = f[q.front()] + nums[i];
while(q.size() && f[i] >= f[q.back()]) q.pop_back();
q.push_back(i);
}
return f[n-1];
}
};
[Go Back~](# LeetCode题解)
section16-5: 区间DP#
1、戳气球#
class Solution {
public:
int maxCoins(vector<int>& nums) {
int n=nums.size();
nums.insert(nums.begin(),1); nums.push_back(1);
vector<vector<int>> f(n+2,vector<int>(n+2,0));
for(int len=1;len<=n;len++){
for(int i=1;i+len-1<=n;i++){
int j=i+len-1;
for(int k=i;k<=j;k++){
f[i][j] = max(f[i][j], f[i][k-1]+f[k+1][j]+nums[i-1]*nums[k]*nums[j+1]);
}
}
}
return f[1][n];
}
};
2、猜数字大小 II#
class Solution {
public:
int getMoneyAmount(int n) {
vector<vector<int>>f(n+2,vector<int>(n+2,0));
for(int len=2;len<=n;len++){
for(int i=1;i+len-1<=n;i++){
int j=i+len-1;
f[i][j] = 0x3f3f3f3f;
for(int k=i;k<=j;k++){
f[i][j] = min(f[i][j], max(f[i][k-1], f[k+1][j])+k);
}
}
}
return f[1][n];
}
};
3、预测赢家#
1、我们可以简化算法 1 中的状态表示,我们设表示闭区间$ [i, j] f(i,i)=nums[i]f(i,j)=max(−f(i+1,j)+nums[i],−f(i,j−1)+nums[j]) f(i,j)$是否大于等于 0。
class Solution {
public:
bool PredictTheWinner(vector<int>& nums) {
int n=nums.size();
vector<vector<int>> f(n+1, vector<int>(n+1,0));
for(int len=1;len<=n;len++){
for(int i=1;i+len-1<=n;i++){
int j=i+len-1;
if(len==1) f[i][j] = nums[i-1];
else{
f[i][j] = max(-f[i+1][j]+nums[i-1], -f[i][j-1]+nums[j-1]);
}
}
}
return f[1][n]>=0;
}
};
4、最长回文子序列#
class Solution {
public:
int longestPalindromeSubseq(string s) {
int n=s.size();
vector<vector<int>> f(n+2,vector<int>(n+2,0));
f[0][0]=1;
for(int i=1;i<=n;i++) f[i][i]=1;
for(int len=2;len<=n;len++){
for(int i=1;i+len-1<=n;i++){
int j=i+len-1;
if(s[i-1] == s[j-1]) f[i][j] = max(f[i][j], 2+f[i+1][j-1]);
else f[i][j] = max(f[i+1][j], f[i][j-1]);
}
}
return f[1][n];
}
};
5、统计不同回文子序列 【×】区间dp+双端队列#
class Solution {
public:
int countPalindromicSubsequences(string s) {
int n=s.size(); const int mod=1e9+7;
vector<vector<int>> f(n+2,vector<int>(n+2,1));
f[0][0] = 1;
for(int i=1;i<=n;i++) f[i][i]++;
for(int len=2;len<=n;len++){
deque<int> q[4];
for(int i=1;i<=n;i++){
q[s[i-1]-'a'].push_back(i);
int j=i-len+1;
if(j>=1){
for(int k=0;k<4;k++){
while(q[k].size() && q[k].front() < j) q[k].pop_front();
if(q[k].size()){
f[j][i] ++ ;
int l = q[k].front(), r = q[k].back();
if (l < r)
f[j][i] = (f[j][i] + f[l + 1][r - 1]) % mod;
}
}
}
}
}
return (f[1][n]+mod-1)%mod;
}
};
6、石子游戏 【思路同题3】#
class Solution {
public:
bool stoneGame(vector<int>& piles) {
int n=piles.size();
vector<vector<int>>f(n+2,vector<int>(n+2,0));
for(int i=1;i<=n;i++) f[i][i]=piles[i-1];
for(int len=2;len<=n;len++){
for(int i=1;i+len-1<=n;i++){
int j=i+len-1;
f[i][j] = max(-f[i+1][j]+piles[i-1], -f[i][j-1]+piles[j-1]);
}
}
return f[1][n]>0;
}
};
7、石子游戏 VII#
转移:
class Solution {
public:
int stoneGameVII(vector<int>& stones) {
int n=stones.size();
vector<int> sum(n + 1, 0);
for (int i = 1; i <= n; i++)
sum[i] = sum[i - 1] + stones[i - 1];
vector<vector<int>> f(n+2,vector<int>(n+2,-0x3f3f3f));
for (int i = 1; i <= n; i++) f[i][i] = 0;
for(int len=2;len<=n;len++){
for(int i=1;i+len-1<=n;i++){
int j=i+len-1;
f[i][j] = max(sum[j]-sum[i]-f[i+1][j], sum[j-1]-sum[i-1]-f[i][j-1]);
}
}
return f[1][n];
}
};
[Go Back~](# LeetCode题解)
section16-6: 记忆化搜索#
1、【树形dp】打家劫舍 III#
class Solution {
public:
int rob(TreeNode* root) {
auto f = dfs(root);
return max(f[0],f[1]);
}
vector<int> dfs(TreeNode* root){
if(!root) return {0,0};
auto x = dfs(root->left), y = dfs(root->right);
return {max(x[0],x[1]) + max(y[0],y[1]) , (x[0] + y[0] + root->val)};
}
};
class Solution {
public:
unordered_map<TreeNode*, unordered_map<int,int>> hash;
int rob(TreeNode* root) {
dfs(root);
return max(hash[root][0],hash[root][1]);
}
void dfs(TreeNode*root){
if(!root) return;
dfs(root->left), dfs(root->right);
hash[root][0] = max(hash[root->left][0], hash[root->left][1]) + max(hash[root->right][0], hash[root->right][1]);
hash[root][1] = root->val + hash[root->left][0] + hash[root->right][0];
}
};
2、分发糖果#
class Solution {
public:
int candy(vector<int>& ratings) {
// 贪心
int n=ratings.size();
vector<int>f(n,1);
for(int i=0;i<n;i++) if(i && ratings[i-1]<ratings[i]) f[i]=f[i-1]+1;
for(int i=n-1;~i;i--) if(i+1 != n && ratings[i+1] < ratings[i]) f[i]=max(f[i+1]+1,f[i]);
return accumulate(f.begin(),f.end(),0);
}
};
class Solution {
public:
vector<int> f;
int n;
int candy(vector<int>& ratings) {
// 记忆搜索
n=ratings.size();
f.resize(n,-1);
int ans=0;
for(int i=0;i<n;i++)
ans+=dfs(ratings,i);
return ans;
}
int dfs(vector<int>&ratings, int i){
if(f[i]!=-1) return f[i];
f[i]=1;
if(i+1<n && ratings[i+1]<ratings[i])
f[i] = max(f[i],dfs(ratings,i+1)+1);
if(i-1>=0 && ratings[i-1]<ratings[i])
f[i] = max(f[i],dfs(ratings,i-1)+1);
return f[i];
}
};
3、矩阵中的最长递增路径 【对应-滑雪acwing】#
class Solution {
public:
int dx[4]={-1,0,1,0}, dy[4]={0,-1,0,1};
vector<vector<int>>f;
int n,m;
int longestIncreasingPath(vector<vector<int>>& matrix) {
n=matrix.size(), m=matrix[0].size();
f=vector<vector<int>>(n,vector<int>(m,-1));
int ans=0;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
ans=max(ans,dfs(matrix,i,j));
return ans;
}
int dfs(vector<vector<int>>&matrix, int i, int j){
if(f[i][j] != -1) return f[i][j];
f[i][j]=1;
for(int k=0;k<4;k++){
int x=dx[k]+i, y=dy[k]+j;
if(x>=0 && x<n && y>=0 && y<m && matrix[i][j]<matrix[x][y]){
f[i][j] = max(f[i][j], 1+dfs(matrix,x,y));
}
}
return f[i][j];
}
};
4、我能赢吗 【×】#
class Solution {
public:
vector<int> f;
int n;
bool canIWin(int m, int total) {
n=m;
if((n+1)*n < 2*total) return false;
if(!total) return true;
f.resize(1<<(n+1),-1);
return dfs(0,total);
}
bool dfs(int u, int t){
if(f[u]!=-1) return f[u];
if(t<=0) return f[u]=false;
for(int i=1;i<=n;i++){
if(!(u & 1<<i)){
if(!dfs(u+(1<<i), t-i))
return f[u]=true;
}
}
return f[u]=false;
}
};
5、猫和老鼠#
class Solution {
public:
int n;
vector<vector<vector<int>>> f;
vector<vector<int>> g;
int dfs(int k,int i,int j){
int &v=f[k][i][j];
if (v!=-1) return v;
if (k>2*n) return v=0;
if (i==0) return v=1;
if (i==j) return v=2;
if (k%2==0){
bool draw=false;
for (int ne:g[i]){
int ans=dfs(k+1,ne,j);
if (ans==1) return v=1;
if (ans==0) draw=true;
}
if (draw) return v=0;
return v=2;
}else{
bool draw=false;
for (int ne:g[j]){
if (ne==0) continue;
int ans=dfs(k+1,i,ne);
if (ans==2) return v=2;
if (ans==0) draw=true;
}
if (draw) return v=0;
return v=1;
}
}
int catMouseGame(vector<vector<int>>& graph) {
g=graph;
n=g.size();
f=vector<vector<vector<int>>>(2*n+2,vector<vector<int>>(n,vector<int>(n,-1)));
return dfs(0,1,2);
}
};
[Go Back~](# LeetCode题解)
section16-7: 状态机dp+状压dp#
1、最佳买卖股票时机含冷冻期#
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n=prices.size();
vector<vector<int>> f(n,vector<int>(2,0));
f[0][0] = 0, f[0][1] = -prices[0];
for(int i=1;i<n;i++){
f[i][0] = max(f[i-1][0], f[i-1][1]+prices[i]);
if(i>=2) f[i][1] = max(f[i-1][1], f[i-2][0]-prices[i]);
else f[i][1] = max(f[i-1][1], -prices[i]);
}
return f[n-1][0];
}
};
// 状态压缩
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n=prices.size();
int a0 = 0, a1 = -prices[0];
int last_a0=a0, last_a1 = a1, last_a2=0;
for(int i=1;i<n;i++){
a0 = max(last_a0, last_a1+prices[i]);
if(i>=2) a1 = max(last_a1, last_a2-prices[i]);
else a1 = max(last_a1, -prices[i]);
last_a2 = last_a0; last_a1 = a1; last_a0 = a0;
}
return a0;
}
};
2、学生出勤记录 II#
const int mod=1e9+7;
class Solution {
public:
int checkRecord(int n) {
vector<vector<vector<int>>>f(n+1,vector<vector<int>>(2,vector<int>(3,0)));
f[0][0][0]=1;
for(int i=0;i<n;i++){
for(int j=0;j<2;j++){
for(int k=0;k<3;k++){
if(!j) f[i+1][j+1][0] = (f[i+1][j+1][0]+f[i][j][k]) % mod;
if(k+1<=2) f[i+1][j][k+1] = (f[i+1][j][k+1] + f[i][j][k]) % mod;
f[i+1][j][0] = (f[i+1][j][0] + f[i][j][k]) % mod;
}
}
}
int res=0;
for(int j=0;j<2;j++)
for(int k=0;k<=2;k++)
res = (res+f[n][j][k])%mod;
return res;
}
};
3、买卖股票的最佳时机含手续费#
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n=prices.size();
vector<int> f(n,0), g(n,0);
f[0]=0, g[0]=-prices[0];
for(int i=1;i<n;i++){
f[i] = max(f[i-1], g[i-1]+prices[i]-fee);
g[i] = max(g[i-1], f[i-1]-prices[i]);
}
return f[n-1];
}
};
// 状态压缩
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n=prices.size();
int a0=0, b0=-prices[0];
for(int i=1;i<n;i++){
int last_a0 = a0, last_b0 = b0;
a0 = max(last_a0, last_b0+prices[i]-fee);
b0 = max(last_b0, last_a0-prices[i]);
}
return a0;
}
};
4、我能赢吗 【×】#
class Solution {
public:
vector<int> f;
int n;
bool canIWin(int m, int total) {
n=m;
if((n+1)*n < 2*total) return false;
if(!total) return true;
f.resize(1<<(n+1),-1);
return dfs(0,total);
}
bool dfs(int u, int t){ // 是否使用的状态通过整数u表示
if(f[u]!=-1) return f[u];
if(t<=0) return f[u]=false;
for(int i=1;i<=n;i++){
if(!(u & 1<<i)){
if(!dfs(u+(1<<i), t-i))
return f[u]=true;
}
}
return f[u]=false;
}
};
[Go Back~](# LeetCode题解)
作者: SrtFrmGNU
出处:https://www.cnblogs.com/SrtFrmGNU/p/15891058.html
版权:本站使用「CC BY 4.0」创作共享协议,转载请在文章明显位置注明作者及出处。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 三行代码完成国际化适配,妙~啊~
· .NET Core 中如何实现缓存的预热?