Different Circle Permutation （HDU - 5868） （欧拉函数+矩阵快速幂）

题目：

You may not know this but it's a fact that Xinghai Square is Asia's largest city square. It is located in Dalian and, of course, a landmark of the city. It's an ideal place for outing any time of the year. And now: 
   
  There are NN children from a nearby primary school flying kites with a teacher. When they have a rest at noon, part of them (maybe none) sit around the circle flower beds. The angle between any two of them relative to the center of the circle is always a multiple of 2πN2πN but always not 2πN2πN. 
   
  Now, the teacher raises a question: How many different ways there are to arrange students sitting around the flower beds according to the rule stated above. To simplify the problem, every student is seen as the same. And to make the answer looks not so great, the teacher adds another specification: two ways are considered the same if they coincide after rotating.

InputThere are TT tests (T≤50T≤50). Each test contains one integer NN. 1≤N≤1000000000 (109)1≤N≤1000000000 (109). Process till the end of input.OutputFor each test, output the answer mod 1000000007 (109+7109+7) in one line.Sample Input

4
7
10

Sample Output

3
5
15


解题报告：这个题目一开始可以根据手算推导出前边的数，然后根据oeis可以快速找到该序列的规律

 

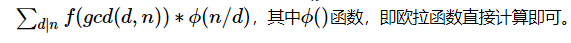
这个，咱们直接去求解n的所有因子d，eluer(n/d)*(f(d+1)+f(d-1)),所有结果求和，然后除以n,这个时候需要使用逆元。

 

ac代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long ll;
int T;
ll n;
const ll mod=1e9+7;
const int maxn=1e5+1000;
int f[maxn];
int phi[maxn];

void db_f()
{
	f[1]=1;
	f[2]=3;
	for(int i=3;i<maxn;i++)
		f[i]=(f[i-1]+f[i-2])%mod;
}
ll ksm(ll a,ll b)
{
	ll res=1;
	a%=mod;
	while(b)
	{
		if(b&1)
			res=(res*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}
	return res;
}
ll eluer(ll n)
{
	ll res=n;
	for(int i=2;i*i<=n;i++)
	{
		if(n%i==0)
			res=res/i*(i-1);
		while(n%i==0)
			n/=i;
	}
	if(n>1)
		res=res/n*(n-1);
	return res;
}

struct Mat{
	ll a[5][5];
};
Mat mat_mul(Mat a,Mat b)
{
	Mat c;
	for(int i=0;i<2;i++)
	{
		for(int j=0;j<2;j++)
		{
			c.a[i][j]=0;
			for(int k=0;k<2;k++)
			{
				c.a[i][j]+=a.a[i][k]*b.a[k][j];
				c.a[i][j]%=mod;
			}
		}
	}
	return c;
}

Mat mat_ksm(Mat a,ll n)
{
	Mat res;
	res.a[0][0]=res.a[1][1]=1;
	res.a[0][1]=res.a[1][0]=0;
	
	while(n)
	{
		if(n&1) res=mat_mul(res,a);
		a=mat_mul(a,a);
		n>>=1;
	}
	return res;
}

ll get_f(int n)
{
	if(n<100000)
		return f[n]; 
	Mat a;
	a.a[0][0]=1;
	a.a[0][1]=1;
	a.a[1][0]=1;
	a.a[1][1]=0;
	a=mat_ksm(a,n-2);
	return 3*a.a[0][0]+a.a[0][1];
}
int main()
{
	db_f();
	while(scanf("%d",&n)!=EOF)
	{
		if(n==1)
		{
			printf("2\n");
			continue;
		}
		ll ans=0;	
		for(ll i=1;i*i<=n;i++)
		{
			if(n%i==0)
			{
				ll tmp=(get_f(i)%mod*eluer(n/i)%mod);
				ans=(ans+tmp)%mod;
				if(i*i!=n)
				{
					ll j=n/i;
					tmp=get_f(j)%mod*eluer(n/j)%mod;
					ans=(ans+tmp)%mod;
				}
			}
		}
		printf("%lld\n",(ans*ksm(n,mod-2)%mod)%mod);
	}
}