【知识点复习】最短路
前言
我好菜
参考链接：最短路算法总结（超详细~）
介绍
最短路，顾名思义，图上最短的路径（我真的好敷衍啊
最短路有五种常规方法，分为单源和多源，单源即起点确定的最短路，多源即起点终点不定的最短路。
稠密图用邻接矩阵存，稀疏图用邻接表存储。
稠密图： \(m\) 和 \(n^2\) 一个级别
稀疏图： \(m\) 和 \(n\) 一个级别
下面有张图。
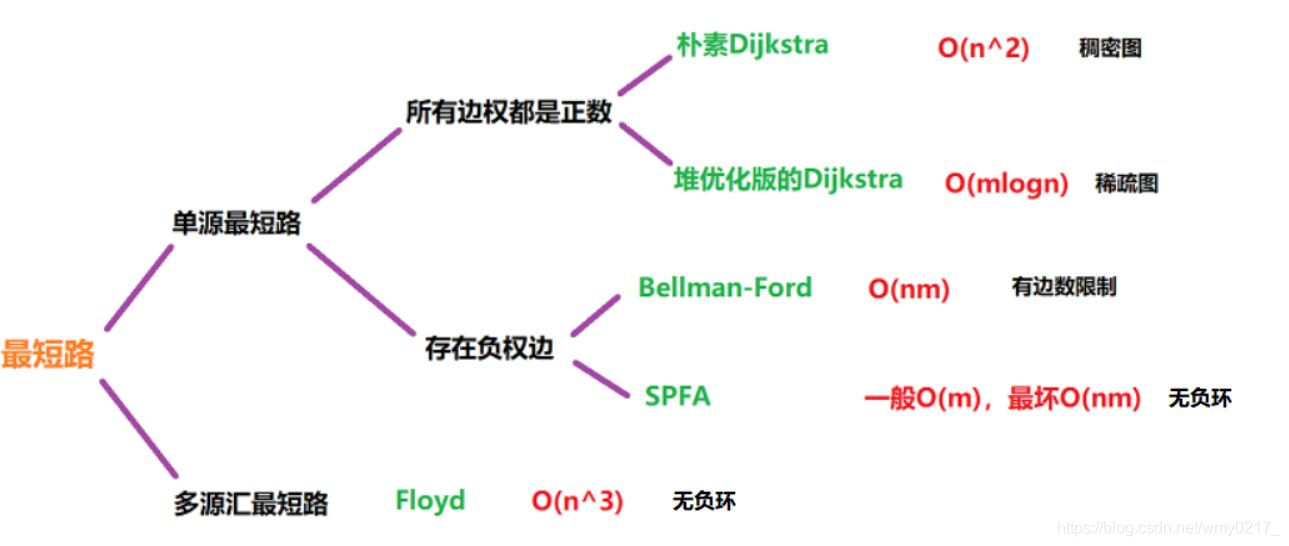
具体讲解可以看参考链接，我比较懒菜，不想写了。
单源
一般常用 \(Dijkstra\)。因为关于 \(Spfa\)，它死了（好老的梗啊~
SPFA
大概思路就是，从起点出发，更新每个点的最短路，然后将有更新的点放进队列中，不断更新各个点的最短路和队列，知道队列为空。
最长路也是同样思路，只需要更改比较方式即可。
void spfa(int f, int s) {
queue<int> q;
q.push(s);
memset(vis, 0, sizeof(vis));
memset(dis[f], -0x3f, sizeof(dis[f]));
int now, ver;
vis[s] = 1, dis[f][s] = val[s];
while(!q.empty()) {
now = q.front(), q.pop(), vis[now] = 0;
for(int i = head[f][now]; i; i = nex[f][i]) {
ver = to[f][i];
if(dis[f][ver] < max(dis[f][now], val[ver])) {
dis[f][ver] = max(dis[f][now], val[ver]);
if(!vis[ver]) q.push(ver), vis[ver] = 1;
}
}
}
}
Dijkstra
for(int i=0; i<n; i++)
{
int t = -1;
for(int j=1; j<=n; j++) // 在没有确定最短路中的所有点找出距离最短的那个点 t
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t=j;
st[t]=true; // 代表 t 这个点已经确定最短路了
for(int j=1; j<=n; j++) // 用 t 更新其他点的最短距离
dist[j] = min(dist[j],dist[t]+g[t][j]);
}
另外，可以堆优化，但貌似不常用……感兴趣的，看参考博客吧。
多源（Floyd 算法）
其实说白点就是一个 \(n^3\) 的暴力枚举……
但是要记得，\(k\) 是在最外层循环的。
void floyd()
{
for(int k=1; k<=n; k++)
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
应用
SPFA 判负环
记录每个点最短路所经过的边数 \(cnt\)，当 \(cnt\) \(>=\) \(n\) 时，说明该点最短路经过了至少 \(n\) 条边（等同于经过了至少 \(n\) 个点，该最短路经过了同一点至少两次），即可说明存在负环。
因为只有负环才会让dist距离变小，否则我们为什么要两次经过同一个点呢。
int spfa()
{
queue<int> q;
for(int i=1; i<=n; i++) //将所有结点入队
{
st[i] = true;
q.push(i);
}
while(q.size()) // 队列不空
{
int t = q.front(); //取队头
q.pop();
st[t] = false; // 代表这个点已经不在队列了
for(int i = h[t]; i!=-1; i=ne[i]) // 更新 t 的所有临边结点的最短路
{
int j = e[i];
if(dist[j] > dist[t]+w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1; // t到起点的边数+1
if(cnt[j] >= n) return true;// 存在负环
if(!st[j]) //如果 j 不在队列，让 j 入队
{
q.push(j);
st[j] = true; // 标记 j 在队中
}
}
}
}
return false;// 不存在负环
}
其他
一般最短路都不单独使用，会跟其他算法结合起来（废话）
练习
\(Acwing\) 和洛谷都有呢。
[\(Acwing\)题单]（https://www.acwing.com/activity/content/punch_the_clock/6/）
