【知识点复习】基环树
前言
emmmm
从前有棵树,树上有个环,环里有个小和尚,小和尚在讲故事。讲的是什么呢?从前有棵树,树上有个环,环里有个小和尚,小和尚在讲故事。讲的是什么呢?从前有棵树……
算法概述
基环树啊,经过我粗浅的学习,认为它是将环和树边分开处理,具体来说就是每次强制断掉环中的任意一条边来处理。(我觉得说不上算法,可能只是一种数据结构或者巧妙的思想?
反正就是很妙啊。。。
定义
基环树,也是环套树,一种有 \(n\) 个点 \(n\) 条边 的图, 即在一棵 \(n\) 个点的树的基础上在任意两点(没有直接连边)之间在连上一条边的图。
可能有点抽象其实还好,看看下面我盗的图吧(
- 无向树
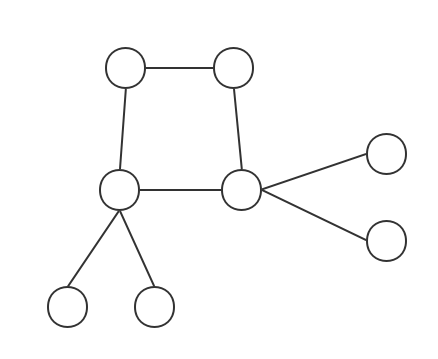
- 外向树
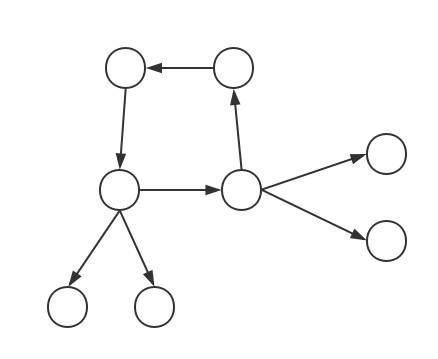
- 内向树
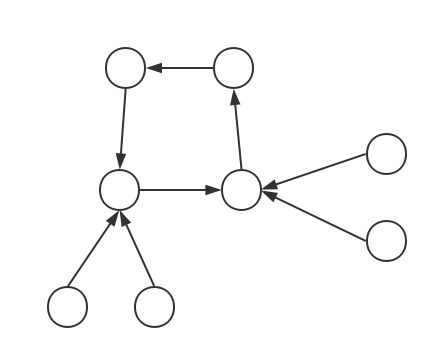
所以基环树的性质不多,根据上面我们就可以得到最显然的一条:
- 点数与边数相同。
 就这?!
就这?!
对没错,就这(
前置知识
拓扑排序
用来处理无向图,找到环上的每一个点啦。
基本流程:
- 找到入度为 \(1\) 的点入队
- 每次取出队首,将与队首相连的所有点的入度分别减 \(1\)
- 重复以上操作,知道队列为空
void t_sort() {
int l = 0, r = 0, now, ver;
for(int i = 1; i <= n; i ++) {
if(in[i] == 1) sta[++r] = i;
}
while(l < r) {
now = sta[++l];
for(int i = head[now]; i; i = e[i].nex) {
ver = e[i].to;
in[ver] --;
if(in[ver] == 1) sta[++r] = i;
}
}
}
这样处理之后,按理来说所有点的入度都应该 \(\le\) \(1\), 但是因为有环,所以存在入度 \(\ge\) \(1\)。
所以在拓扑之后,再搜一遍,入度 \(\ge\) \(1\) 的都是环上的点, 就找到整个环的位置啦~
DFS
这个没什么要讲的。
void dfs(int x) {
int ver;
sta[++cnt] = x, vis[x] = 1;
for(int i = head[x]; i; i = e[i].nex) {
ver = e[i].to;
if(rel[x][ver] || vis[ver]) continue;
dfs(ver);
}
}
注意: \(dfs\) 的代码并没有模板化,上面给出的代码仅仅只是为了介绍 \(dfs\),并不是用于所有的基环树。具体实现要看题目要求而定。
应用
断环法
应该算是最常见的方法吧?
顾名思义,断环法其实就是每次通过断掉环上任意一条边,使其变成一棵 \(n - 1\) 条边的树,在树上跑一遍答案。最后取满足条件的最大值或者最小值。
这样感觉就是暴力嘛,所以只适用于数据范围很小而且环的存在(也就是断掉环上的一条边之后)不会影响答案的情况。
经典例题: [NOIP2018 提高组] 旅行
在一个连通的 \(n\) 个点 \(n - 1\) 或者 \(n\) 条边的无向图上,从任意一点出发,沿边遍历每一个点,求字典序最小的遍历顺序。
要求字典序最小,那肯定是从 \(1\) 开始的撒。
-
对于 \(n - 1\) 条边来说,直接从 \(1\) 开始,在所有连边中选择字典序最小的点走,一直把所有点走完就好了。这可以通过提前将边按字典序排序预处理实现。
-
对于 \(n\) 条边,就是我们刚才说的 断环法。
先找到环,每次断掉其中一条边,按照 \(n - 1\) 边的方法遍历一遍,再去字典序最小的走法就好了。
具体实现看代码吧,应该很好懂的。
点击查看代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 5e3 + 5;
bool vis[N], rel[N][N];
int n, m, sta[N], tot = 1, cnt, head[N], in[N], d[N], lu[N], fa[N], ans[N];
struct node {
int to,nex;
}e[N << 1];
struct edge {
int u,v;
}s[N << 1];
bool cmp(edge x,edge y) {
return x.v > y.v;
}
void add(int x,int y) {
e[++tot] = (node) {y,head[x]}, head[x] = tot, in[y] ++;
}
void tp() {
int l = 0, r = 0;
for(int i = 1; i <= n; i ++) {
if(in[i] == 1) sta[++r] = i;
}
tot = r;int ver, now;
while(l < r) {
now = sta[++l];
for(int i = head[now]; i; i = e[i].nex) {
ver = e[i].to, in[ver] --;
if(in[ver] == 1) sta[++r] = ver;
}
}
}
void dfs(int x) {
int ver;
sta[++cnt] = x, vis[x] = 1;
for(int i = head[x]; i; i = e[i].nex) {
ver = e[i].to;
if(rel[x][ver] || vis[ver]) continue;
dfs(ver);
}
}
void check() {
int i,flag = 0;;
for(i = 1; i <= n; i ++) {
if(sta[i] < ans[i]) {flag = 1; break;}
else if(ans[i] < sta[i]) return;
}
if(!flag) return;
for(; i <= n; i ++) ans[i] = sta[i];
}
void get_ans(int x) {
int u = x, tmp = 0, i, ver;
do {
lu[++tmp] = u, in[u] = 1;
for(i = head[u]; i; i = e[i].nex) {
ver = e[i].to;
if(in[ver] > 1) {u = ver; break;}
}
}while(i);
lu[++tmp] = x;
for(int i = 1; i < tmp; i ++) {
rel[lu[i]][lu[i + 1]] = rel[lu[i + 1]][lu[i]] = 1;
memset(vis,0,sizeof(vis));
cnt = 0, dfs(1), check();
rel[lu[i]][lu[i + 1]] = rel[lu[i + 1]][lu[i]] = 0;
}
}
int main() {
int u,v;
scanf("%d %d",&n,&m);
for(int i = 1; i <= m; i ++) {
scanf("%d %d",&u,&v);
s[i] = (edge) {u,v};
s[i + m] = (edge) {v,u};
ans[i] = 1e5;
}
ans[n] = 1e5;
sort(s + 1,s + 1 + 2 * m,cmp);
for(int i = 1; i <= 2 * m; i ++) add(s[i].u,s[i].v);
if(m == n - 1) {
dfs(1);
for(int i = 1; i <= n; i ++) printf("%d ",sta[i]);
return 0;
}
tp();
for(int i = 1; i <= n; i ++) {
if(in[i] > 1) {
get_ans(i);
break;
}
}
for(int i = 1; i <= n; i ++) printf("%d ",ans[i]);
return 0;
}
推荐题目: emmm……我暂时还没有碰到,有的话会挂上来的。
二次DP法
二次 \(dp\), 二次 \(dp\), 其实就是先把环断开一条边 \((x,y)\),以 \(x\) 为起点做一次 \(dp\) , 以 \(y\) 为起点再做一次 \(dp\)。
经典例题: [ZJOI2008]骑士
在一个不保证连通的 \(n\) 个点 \(n\) 条边的无向图上,每个点有点权,相邻两个点不能同时选择,求选出的点权和的最大值。
因为题目不保证连通,所以我们每次选择一个连通块,通过 二次\(dp\) 求得最大点权和,累加到答案里就好了。
而重点就在于如何求连通块的最大值?
因为我们建的是有向边(详细讲解见洛谷题解区),分析得到一个性质就是:每个联通块内有且只有一个简单环
为了能够 \(dp\),我们要删去环上的一条边 \((x,y)\),但是 \(x\) 和 \(y\) 不能同时选择,所以我们强制使任意一点不能被选,对当前新树跑一遍 \(dp\)。
一共要跑两次,所以就叫二次 \(DP\)。
\(dp\) 部分跟没有上司的舞会基本一致,这里就不过多赘述了。
其实就是,对于一个点的两种情况:
-
被选,那它的子节点就不能被选
-
没有被选,它的子节点可选可不选,取最大值。
从起点开始,往下 \(dp\) 到根节点,一路更新答案就好了。。
这道题简化建边的思想很妙啊,一定要去康康!!
详见代码。
点击查看代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
const int N = 1e6 + 5;
bool vis[N];
ll ans, res, dp[N][2];
int n, a[N], sta[N], tot, tmp, head[N], w[N], fa[N];
struct node {
int to,nex;
}e[N << 1];
void add(int x,int y) {
e[++tot] = (node) {y,head[x]}, head[x] = tot;
}
void dfs(int x) {
int ver;
vis[x] = 1;
dp[x][0] = 0, dp[x][1] = w[x];
for(int i = head[x]; i; i = e[i].nex) {
ver = e[i].to;
if(ver == tmp) dp[ver][1] = -1e9;
else {
dfs(ver);
dp[x][0] += max(dp[ver][0],dp[ver][1]);
dp[x][1] += dp[ver][0];
}
}
}
void find_cir(int x) {
vis[x] = 1;
if(vis[a[x]]) tmp = x;
else find_cir(a[x]);
}
int main() {
scanf("%d",&n);
for(int i = 1; i <= n; i ++) {
scanf("%d %d",&w[i],&a[i]);
add(a[i],i);
}
for(int i = 1; i <= n; i ++) {
if(vis[i]) continue;
find_cir(i), dfs(tmp);
res = max(dp[tmp][1],dp[tmp][0]);
tmp = a[tmp], dfs(tmp);
ans += max(res,max(dp[tmp][0],dp[tmp][1]));
}
printf("%lld",ans);
return 0;
}
断环复制法
同样可以顾名思义,就是以一个点为起点把环拆开,然后复制一遍放在后面,长度变为原来的两倍。
这样就可以处理所有以任意点为起点的拆环方案了。
这种方法一般适用于基环树森林,或者存在多个基环树需要同时维护的情况。
经典例题: [IOI2008]Island
你准备浏览一个公园,该公园由 \(N\) 个岛屿组成,当地管理部门从每个岛屿 \(i\) 出发向另外一个岛屿建了一座长度为 \(L_i\) 的桥,不过桥是可以双向行走的。同时,每对岛屿之间都有一艘专用的往来两岛之间的渡船。相对于乘船而言,你更喜欢步行。你希望经过的桥的总长度尽可能长,但受到以下的限制:
- 可以自行挑选一个岛开始游览。
- 任何一个岛都不能游览一次以上。
- 无论任何时间,你都可以由当前所在的岛 \(S\) 去另一个从未到过的岛 \(D\)。从 \(S\) 到 \(D\) 有如下方法:
- 步行:仅当两个岛之间有一座桥时才有可能。对于这种情况,桥的长度会累加到你步行的总距离中。
- 渡船:你可以选择这种方法,仅当没有任何桥和以前使用过的渡船的组合可以由 \(S\) 走到 \(D\) (当检查是否可到达时,你应该考虑所有的路径,包括经过你曾游览过的那些岛)。
注意,你不必游览所有的岛,也可能无法走完所有的桥。
请你编写一个程序,给定 \(N\) 座桥以及它们的长度,按照上述的规则,计算你可以走过的桥的长度之和的最大值。
点击查看代码
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<vector>
using namespace std;
#define ll long long
#define pii pair<int, int>
const int N = 2e6 + 5;
vector< pii > G;
int n, pre[N], q[N << 1];
ll dp[N], val[N], ans, sum[N];
bool vis[N], flag, tag[N << 1];
int tot = 1, head[N], nex[N << 1], to[N << 1], w[N << 1];
void add(int x, int y, int z) {
to[++tot] = y, nex[tot] = head[x], head[x] = tot, w[tot] = z;
}
void dfs(int x, int f) {
vis[x] = 1;
int ver, tmp;
for(int i = head[x]; i; i = nex[i]) {
ver = to[i];
if((i ^ 1) == f || (flag && vis[ver])) continue;
if(vis[ver]) {
tmp = i ^ 1;
do {
G.push_back(make_pair(to[tmp], w[tmp]));
tag[to[tmp]] = 1;
tmp = pre[to[tmp]];
} while(to[tmp] != ver);
G.push_back(make_pair(to[tmp], w[tmp]));
tag[to[tmp]] = flag = 1;
continue;
}
pre[ver] = i ^ 1;
dfs(ver, i);
}
}
ll DP(int x, int f) {
int ver; ll res = 0;
for(int i = head[x]; i; i = nex[i]) {
ver = to[i];
if(ver == f || tag[ver]) continue;
res = max(res, DP(ver, x));
res = max(res, dp[x] + dp[ver] + w[i]);
dp[x] = max(dp[x], dp[ver] + w[i]);
}
return res;
}
ll solve() {
int num = G.size(); ll res = 0;
for(int i = 0; i < num; i ++) {
res = max(res, DP(G[i].first, 0));
val[i] = dp[G[i].first];
sum[i] = G[i].second;
}
memcpy(val + num, val, num * sizeof(ll));
memcpy(sum + num, sum, num * sizeof(ll));
int l = 0, r = -1;
for(int i = 0; i < 2 * num; i ++) {
if(i) sum[i] += sum[i - 1];
while(l <= r && i - q[l] >= num) l ++;
if(l <= r) res = max(res, val[i] + val[q[l]] + sum[i] - sum[q[l]]);
while(l <= r && val[i] - sum[i] >= val[q[r]] - sum[q[r]]) r --;
q[++r] = i;
}
return res;
}
int main() {
scanf("%d", &n);
int v, z;
for(int i = 1; i <= n; i ++) {
scanf("%d %d", &v, &z);
add(i, v, z), add(v, i, z);
}
for(int i = 1; i <= n; i ++) {
if(vis[i]) continue;
flag = 0;
dfs(i, 0);
ans += solve();
G.clear();
}
printf("%lld", ans);
return 0;
}
推荐题单
奇怪的补充
如果像 P1453 城市环路 这种题一样,题面给的是一棵基环树,但是只需要找到树上的环的任意一条边时,直接用并查集就可以了,不用找环。
找到了之后从两个节点出发,分别搜一次就 ok 。
总结
总的来说,基环树还是很巧妙滴~
一般基环树的题都有很明显的特征,要么就是题面直接告诉你这是一棵基环树,要么就是描述为“ \(n\) 点 \(n\) 条边 无重边无自环保证联通”……
这个时候我们就要想到基环树的几种方法,根据题面的其他信息选择合适的一种。找到解题方向之后,就可以 “策码狂奔” 啦hhh~
唔,虽然这是我为了加深印象写给自己的,但是还是希望这篇博客能够帮助正在学习基环树的同学们ヾ(◍°∇°◍)ノ゙
参考博客
本文是基于上面这篇文章的,因为这个屑就是跟着这篇文章学的,所以如有雷同请见谅。跪.jpg


 浙公网安备 33010602011771号
浙公网安备 33010602011771号