CDQ分治学习笔记
前言
最近又做到了 \(CDQ\) 的题目,然鹅我又搞忘了……
╮(╯▽╰)╭
提前声明:因为博主很菜,很多知识都是从其他博客学来的,所以内容多有重复,请见谅!
那么我们一起去康康神仙 \(CDQ\) 的神仙算法吧~
介绍
众所周知,这是神仙 \(CDQ\) (陈丹琪)所发明的离线算法。 敬礼!
适用于解决多重要求的询问。
针对不同问题,可以分为多维偏序问题。
一维偏序
其实一维偏序就差不多跟分治一个性质。而归并排序应该是分治里最具代表性的了,所以下面举归并排序为栗子。
Code
void q_sort(int l,int r) {
if(l==r) return;
int mid=(l+r)>>1;
int i=l,j=mid+1,tot=l;
q_sort(l,mid);
q_sort(mid+1,r);
while(i<=mid && j<=r) {
if(a[i]<=a[j]) b[tot++]=a[i++];
else {
ans+=mid-i+1;
b[tot++]=a[j++];
}
}
while(i<=mid) b[tot++]=a[i++];
while(j<=r) b[tot++]=a[j++];
for(int k=l;k<=r;k++) a[k]=b[k];
}
上面的代码就是归并排序求逆序对(马蜂是以前的,很丑很无辜)。
其实就是将序列不断切分切分,切到只剩下一个时开始与相邻的序列开始比较合并,从而达到较好的排序效果。
因为归并是从短到长逐一合并的,合并前的序列已经是有序的,而合并的过程中是两组队列通过比较选择小的放进序列中,一直到比较完所有序列。
所以整个序列最终的有序性是可以保证的。
而逆序对则是利用合并中两个队列都是有序的性质。
如果 \(a_i > a_j\),就说明从 \(i\) 到 \(mid\) 的所有数字都大于 \(a_j\),因此逆序对数量要加上 \(i\) 到 \(mid\) 的长度 \(mid - i + 1\)。
二维偏序
Desprition
给定 \(n\) 个元素,第 \(i\) 个元素有 \(a_i\) 、\(b_i\) 两个属性,设 \(f(i)\) 表示满足 \(a_j\leq a_i\) 且 \(b_j\leq b_i\) 的 \(j\) 的数量。对于 \(d\in [0,n]\),求满足 \(f(i)=d\) 的数量。
Solution
问题转化,可以将两个变量看成坐标轴上一个点的横纵坐标。那么问题就可以表示为如下的坐标系:
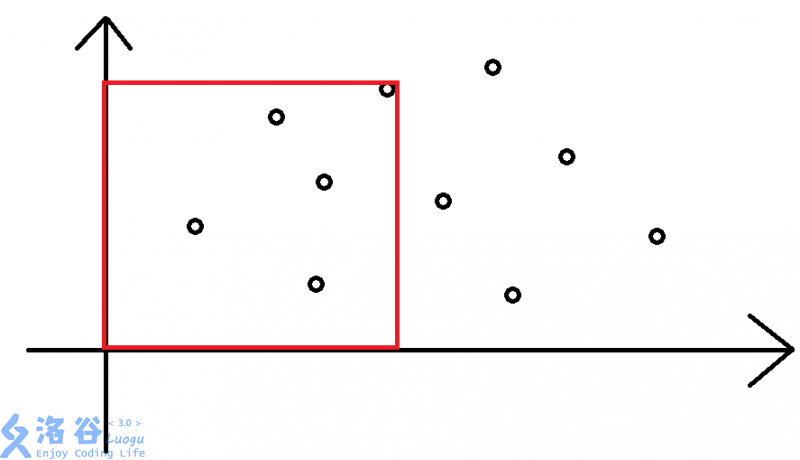
对于每个点,满足条件的结果就是该点与原点形成的矩阵内的点的数量。
所以我们可以先将任意一维从小到大排序,一个点的答案至于它前面的点有关(自动排除了一些不可能情况),然后第二维可以在一维的基础上用 树状数组 维护。每次在求完小于当前值得数量后,再在当前值的位置加一维护即可。
Code
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5 + 5;
int n, m, tmp, tr[N], ans[N];
struct node {
int x,y;
}a[N];
int lowbit(int x) {
return x & (-x);
}
void add(int x,int v) {
for(; x < N; x += lowbit(x)) tr[x] += v;
}
int query(int x) {
int res = 0;
for(; x; x -= lowbit(x)) res += tr[x];
return res;
}
bool cmp(node a,node b) {
return a.x == b.x ? a.y < b.y : a.x < b.x;
}
int main() {
scanf("%d",&n);
for(int i = 1; i <= n; i ++) scanf("%d %d",&a[i].x,&a[i].y);
sort(a + 1,a + 1 + n,cmp);
for(int i = 1; i <= n; i ++) {
tmp = query(a[i].y + 1);
ans[tmp] ++;
add(a[i].y + 1,1);
}
for(int i = 0; i < n; i ++) printf("%d\n",ans[i]);
return 0;
}
三维偏序
可以想到将三个变量存在结构体里,第一维可以直接通过 \(sort\) 先排好序, 第二维使用归并排序, 第三维用树状数组维护。
因为前面提到了归并排序的性质(两个序列在合并前都是有序的),所以在一维排好序的前提下,我们可以保证 \(a_{l1}\) 到 \(a_{mid1}\) 都满足小于等于 \(a_{(mid+1)1}\) 到 \(a_{r1}\),然后再使用归并排序二维。
归并排序时 (\(l\leq i\leq mid\), \(mid+1\leq j\leq r\)), 如果正在比较 \(a_{i2}\) 和 \(a_{j2}\) 且 \(a_{i2} < a_{j2}\), 说明当前情况的前两位符合要求,直接用树状数组维护第三维。
否则不符合情况,当前树状数组位置上的数量就是答案的最大值。
需要注意的是,归并排序每次都会从头再来,因此会出现重复得加,所以在归并排序后要记得清空数组。
例题
Code
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5 + 5;
struct node {
int a,b,c,w,f;
}t[N],e[N];
int n,k,cnt = 1,tr[N * 2],ans[N];
bool cmp(node x,node y) {
if(x.a != y.a) return x.a < y.a;
if(x.b != y.b) return x.b < y.b;
return x.c < y.c;
}
int lowbit(int x) {return x & (-x);}
void add(int x,int val) {
for(; x <= k; x += lowbit(x)) tr[x] += val;
}
int query(int x) {
int res = 0;
for(; x; x -= lowbit(x)) res += tr[x];
return res;
}
void CDQ(int l,int r) {
if(l == r) return;
int mid = (l + r) / 2;
CDQ(l,mid);
CDQ(mid + 1,r);
int p = l,tot = l,q = mid + 1;
while(p <= mid && q <= r) {
if(t[p].b <= t[q].b) {
add(t[p].c,t[p].w);
e[tot++] = t[p++];
}
else {
t[q].f += query(t[q].c);
e[tot++] = t[q++];
}
}
while(p <= mid) {
add(t[p].c,t[p].w);
e[tot++] = t[p++];
}
while(q <= r) {
t[q].f += query(t[q].c);
e[tot++] = t[q++];
}
for(int i = l; i <= mid; i ++) add(t[i].c,-t[i].w);
for(int i = l; i <= r; i ++) {
t[i] = e[i];
//printf("%d %d %d %d %d %d\n",i,t[i].a,t[i].b,t[i].c,t[i].f,t[i].w);
}
}
int main() {
scanf("%d %d",&n,&k);
for(int i = 1; i <= n; i ++) {
scanf("%d %d %d",&t[i].a,&t[i].b,&t[i].c);
t[i].w = 1;
}
sort(t + 1,t + 1 + n,cmp);
for(int i = 2; i <= n; i ++) {
if(t[i].a == t[cnt].a && t[i].b == t[cnt].b && t[i].c == t[cnt].c) t[cnt].w++;
else t[++cnt] = t[i];
}
// printf("%d\n",cnt);
CDQ(1,cnt);
for(int i = 1; i <= cnt; i ++) ans[t[i].f + t[i].w - 1] += t[i].w;
for(int i = 0; i < n; i ++) printf("%d\n",ans[i]);
return 0;
}
四维偏序
需要 \(CDQ\) 套 \(CDQ\) 再套树状数组的东东好变态。。。
可恶!
我亲切地把\(CDQ\) 套 \(CDQ\)称作\(CDQ\)的平方,恩不错,生动形象地表现出了四维的思维跨度之大?
Desprition
给定 \(N\) 个有序四元组 \((a,b,c,d)\),求对于每一个四元组 \((a,b,c,d)\),有多少个四元组 \((a_2,b_2,c_2,d_2)\) 满足 \(a_2<a\) && \(b_2<b\) && \(c_2<c\) && \(d_2<d\)。
Solution
大概过程:
-
对第一维排序
-
第二维 \(cdq\), 递归解决子问题
-
再按第三维顺序合并
-
用树状数组维护第四维
Code
那就咕了吧(▽)
例题
更高维偏序
巨佬的博客没怎么讲,况且蒟蒻不会 \(bitset\) ,所以咱们咕一咕?
通过度娘,我了解到貌似现在最高达到了七维偏序,所以我果断放弃~
或许在我还活着的某一天我会想起来更的。。。
然后我死了……欧耶
CDQ 的拓展应用
我想要讲一下 \(cdq\) 套其他算法的应用~
咕咕咕~
参考博客
[学习笔记]CDQ分治和整体二分
CDQ分治学习笔记
【教程】简易CDQ分治教程&学习笔记
【教程】CDQ套CDQ——四维偏序问题


 浙公网安备 33010602011771号
浙公网安备 33010602011771号