gmoj 6835. 2020.10.31【NOIP提高A组】T1 小h 的几何

题面链接:https://gmoj.net/senior/#main/show/6835

Description

Input

Output

Solution

这道题主要是找结论，找到结论就好做了

对于一个三角形，它的中点三角形的外接圆的圆心就是答案

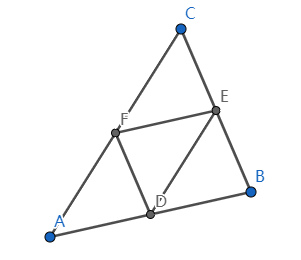
如上图的三角形中，显然\(\triangle ABC \sim\triangle EFD\)

\(\triangle ABC\)的外心O为原点,\(\triangle EFD\)的外心为O'

则\(O'=E+\underset{O'E}{\rightarrow}=\frac{B+C}{2}+\frac{\underset{OA}{\rightarrow}}{2}=\frac{A+B+C}{2}\)

然后对于每个点进行操作

其中对于一个点,它被选中的总方案数是\(\frac{(n-1)(n-2)}{2}\)

而算都不用算,在题面有写,每个点被选中的概率是\(\frac{6}{n(n-1)(n-2)}\)

化简一下就是该点的贡献还要乘上\(\frac{3}{n}\)

时间复杂度\(O(n)\)

#include <cstdio>
#include <cmath>
#define pi 3.1415926535897932384626433832795
#define open(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout);
using namespace std;
int n,i,m;
long double a,x,y;
int main()
{
    open("geometry");
    scanf("%d",&n);
    for (i=1;i<=n;i++)
    {
        scanf("%d",&m);
        a=(m*pi)/(1.0*1e9);
        x+=cos(a)*3/(1.0*n);
        y+=sin(a)*3/(1.0*n);
    }
    printf("%.15Lf %.15Lf",x/2.0,y/2.0);
    return 0;
}