格点统计

题目大意

求第一象限（由于本人思维不算太敏捷，不懂第一象限的只能给你们链接自己看）中，位于反比例函数xy=k的下方（含边界）的格点的个数。

思路详解

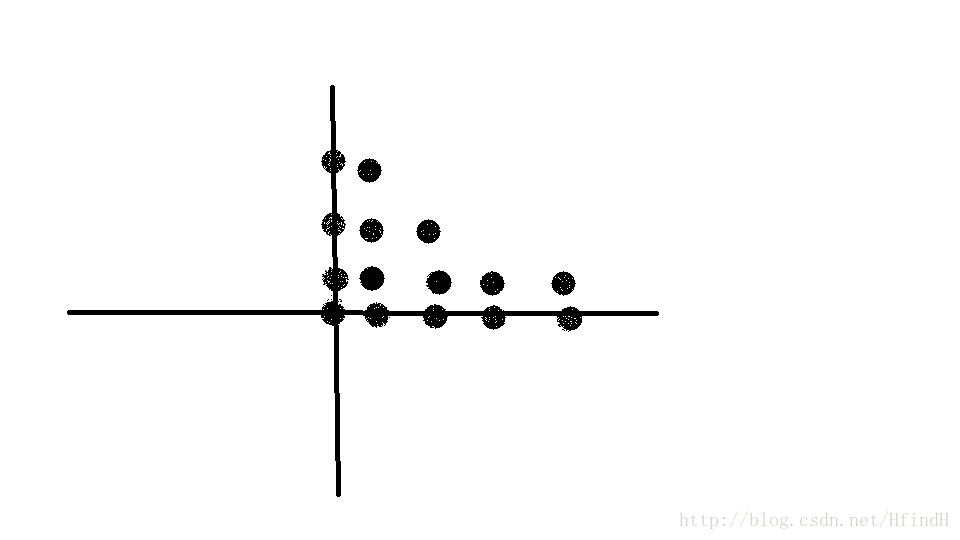
这道题，我们先将第一象限画出来，牛逼的可以脑中构图。

如上图，我画了一个k为4的第一象限图（无视边上的点）于是我们很成功的发现下表

（1,1）	（2,1）	（3,1）	（4,1）
（2,1）	（2,2）
（3,1）
（4,1）

求出来有什么用呢？不用急，一步步来。

1. 我们先按上表打一个为O(n)的程序，一层层做。这样我们的时间复杂度就从O(n^2)--->O(n)。
2. 再仔细观察，我们可以发现，如纵列[(1,1),(2,1),(3,1),(4,1)]与横列[(1,1),(2,1),(3,1),(4,1)]把个数相加，重复了左上角的(1,1)。所以我们可以一层层这么枚举求出规律。首先定义一个len。len=k div i-i+1。这么做便可以求出被前面计算过的数。判断一下，如果这个数大于1，说明除(i,i)点（如（1,1）（2,2）这样的在表中位于左上角的点）外还有数，便将它*2，便能一起求出表这一列的数。但注意，要不能将(i,i)点也乘2，这样会"wrong answer"。这样时间复杂度便可优化到O(trunc(sqrt(k)))。

r
        i,j:longint;
        k,ans,len:int64;
begin
        assign(input,'count.in'); reset(input);
        assign(output,'count.out'); rewrite(output);
        readln(k);
        for i:=1 to trunc(sqrt(k)) do
        begin
                len:=k div i-(i-1);
                if (len>1) then len:=(len-1)*2+1;
                ans:=(ans+len) mod 998244353;
        end;
        writeln(ans mod 998244353);
end.