贝塞尔曲线最近经常接触到,今天研究了一下。
- 原理
关于它的原理,网上有很多。
1.一阶
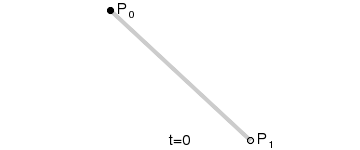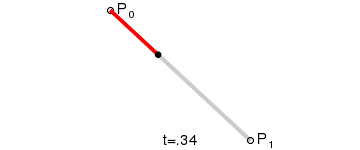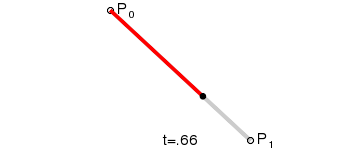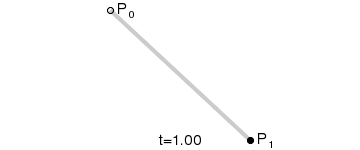
2.二阶

3.多阶

可以看到,多阶可以慢慢降阶为一阶贝塞尔曲线。
1 //一阶 2 private Vector3 BaseBezier(float t,Vector3 pos0,Vector3 pos1) 3 { 4 return pos0 + t * (pos1-pos0); 5 }
递归,降阶为一阶
1 //n阶 2 private Vector3 BezierPro(float t,params Vector3[] posArray) 3 { 4 int l = posArray.Length; 5 6 if (l<2) 7 { 8 return Vector3.zero; 9 } 10 else if (l == 2) 11 { 12 return BaseBezier(t, posArray[0], posArray[1]); 13 } 14 else 15 { 16 Vector3[] tempArray = new Vector3[l-1]; 17 for (int i = 0; i < l-1; i++) 18 { 19 tempArray[i] = BaseBezier(t, posArray[i], posArray[i + 1]); 20 } 21 return BezierPro(t,tempArray); 22 } 23 24 }
在unity里整合:
1 using UnityEngine; 2 using System.Collections; 3 using System.Linq; 4 [ExecuteInEditMode] 5 public class Bezier : MonoBehaviour { 6 public LineRenderer line; 7 public Transform[] PosArray; 8 9 [Range(0,100)] 10 public int sampleCount; 11 // Use this for initialization 12 void Start () { 13 14 } 15 16 // Update is called once per frame 17 void Update () { 18 SetBezier(); 19 } 20 21 //一阶 22 private Vector3 BaseBezier(float t,Vector3 pos0,Vector3 pos1) 23 { 24 return pos0 + t * (pos1-pos0); 25 } 26 //n阶 27 private Vector3 BezierPro(float t,params Vector3[] posArray) 28 { 29 int l = posArray.Length; 30 31 if (l<2) 32 { 33 return Vector3.zero; 34 } 35 else if (l == 2) 36 { 37 return BaseBezier(t, posArray[0], posArray[1]); 38 } 39 else 40 { 41 Vector3[] tempArray = new Vector3[l-1]; 42 for (int i = 0; i < l-1; i++) 43 { 44 tempArray[i] = BaseBezier(t, posArray[i], posArray[i + 1]); 45 } 46 return BezierPro(t,tempArray); 47 } 48 49 } 50 51 [ContextMenu("设置贝塞尔曲线")] 52 private void SetBezier() 53 { 54 if (PosArray.Length<2) 55 { 56 return; 57 } 58 Vector3[] tempArray = new Vector3[PosArray.Length]; 59 60 for (int i = 0; i < PosArray.Length; i++) 61 { 62 tempArray[i] = PosArray[i].position; 63 } 64 65 line.SetVertexCount(sampleCount); 66 for (int i = 0; i < sampleCount; i++) 67 { 68 line.SetPosition(i, BezierPro( (float)i/(float)sampleCount, tempArray) ); 69 } 70 } 71 }
效果展示
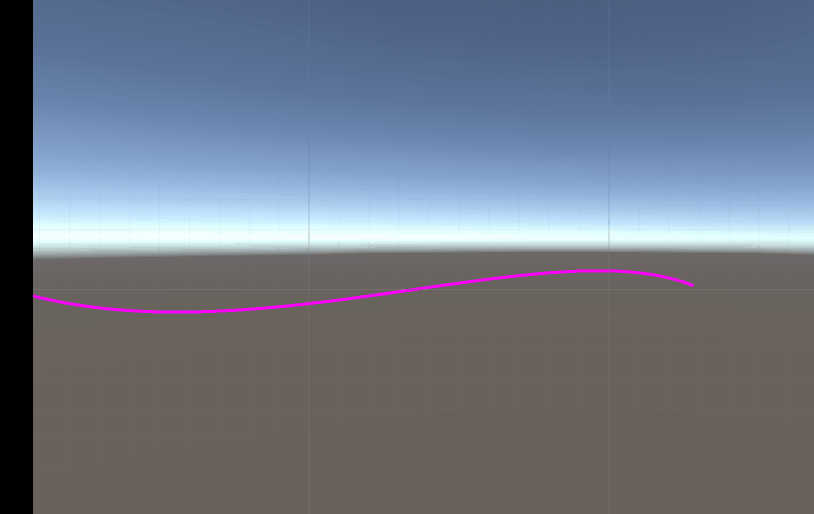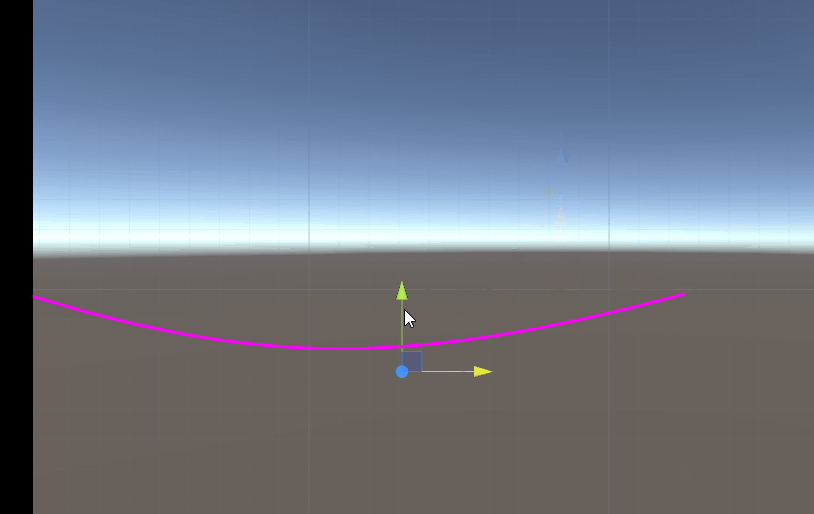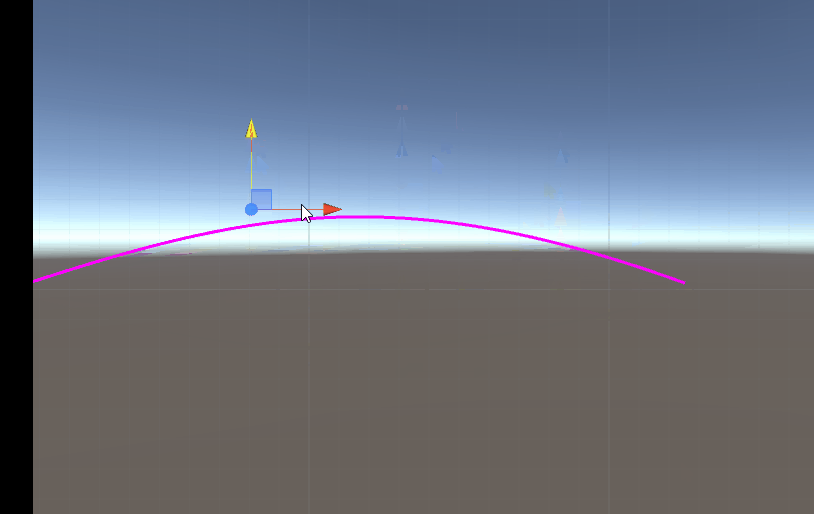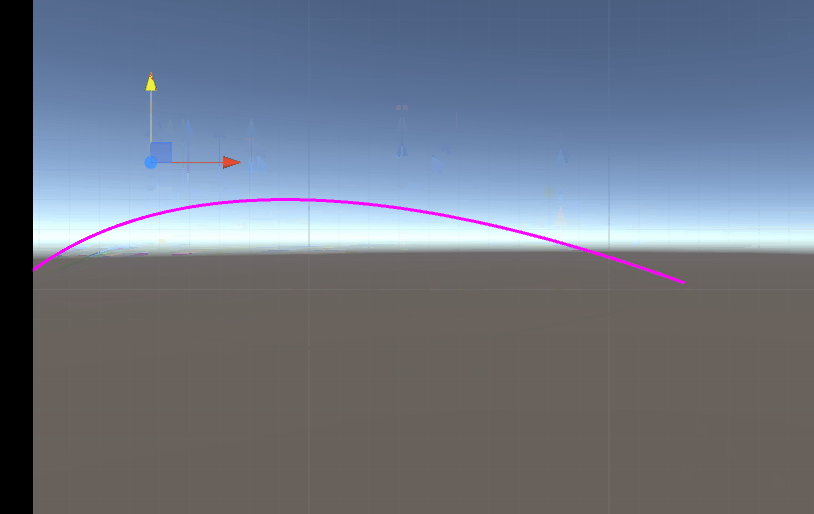



 浙公网安备 33010602011771号
浙公网安备 33010602011771号