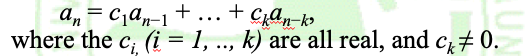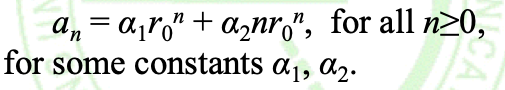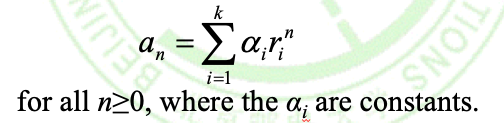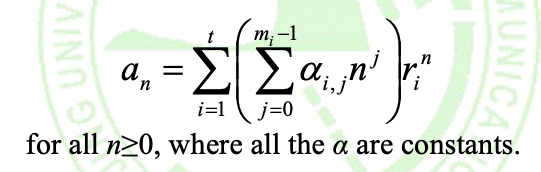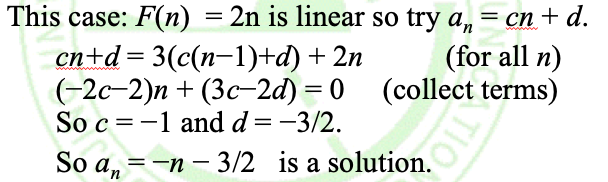8.2解决递推式(Solving Recurrences)

8.2解决递推式(Solving Recurrences)

k阶定常系数线性齐次递推关系(A linear homogeneous recurrence of degree k with constant coefficients)长表示为:

利用特征方程(Characteristic equation)和特征根解决

以2阶定常系数线性齐次递推关系为例:

情况1:有两个不等的根\(r_1≠r_2\)

然后通过初始关系来求得α1 和α2 即可

情况2:有两个相等的根\(r_1 = r_2 = r_0\)

然后通过初始关系来求得α1 和α2 即可

而推广到k阶定常系数线性齐次递推关系

情况3:有k个不等的根

然后通过初始关系来求得αi即可

情况4:有k个根，其中有m个相等的根

然后通过初始关系来求得αi即可

而推广到k阶定常系数线性非齐次递推关系

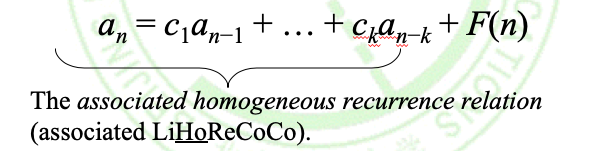
将递推关系拆分分别求通解再通过初始关系求出各个系数即可