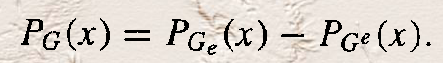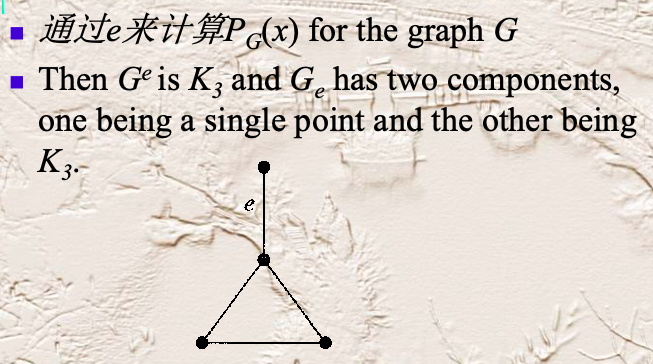10.8图着色(Graph Coloring)

10.8图着色(Graph Coloring)

引入

四色猜想

染色问题

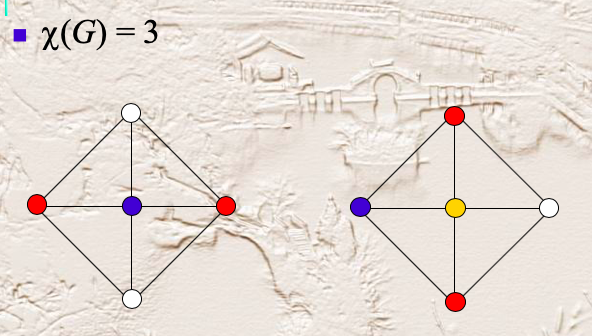
用n中颜色给一副无重边和自环的图染色，要求任意一条边的端点颜色不同；满足情况下使用的最少颜色数称为图G的着色数(chromatic number of G)，记为X(G).

四色定理:

任何平面图都能用4种颜色着色(计算机证明)

五色定理:

任何平面图都能用5种颜色着色

五色定理证明:

引理:所有平面图都至少有一个顶点度数≤5
证明略(平面图不同胚于\(K_5\))

染色多项式(Chromatic Polynomials)

定义\(P_G(n)\)表示对图G用n种颜色进行染色的方法数(n≥0)，\(P_G(n)\)称为G的染色多项式(chromatic polynomial)

可见:最小的使得染色多项式为正数的n值就是X(G)

定理1：

如果图G由互不连通的子图\(G_1,G_2...G_m\)构成，那么有:

拓展：

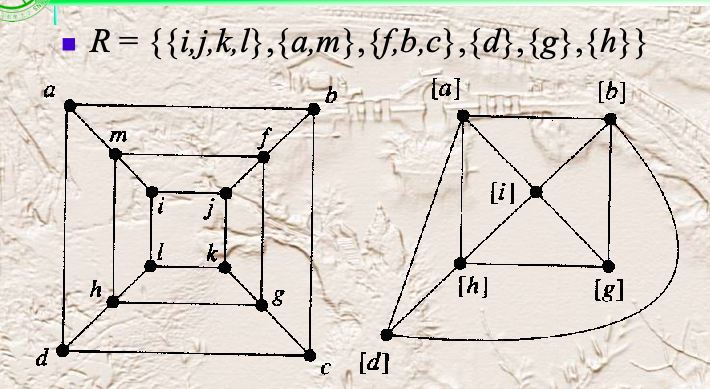
商图(Quotient graph):无重边的图G，通过将按某种规则划分等价类之后得到商图

定理2：

通过一条边e来构建图G的子图:

\(G_e\)：通过删除边e得到的子图，通常会得到两个互不连通的图
\(G^e\)：通过合并e两边的端点得到的G的商图
那么有:

证明略

k阶临界图

称图G是k阶临界图/被k阶染色的(chromatically k-critical)，指的是X(G)=3，且其任意真子图G'的染色数X(G')❤️