10.7平面图(Planar Graphs)
10.7平面图(Planar Graphs)
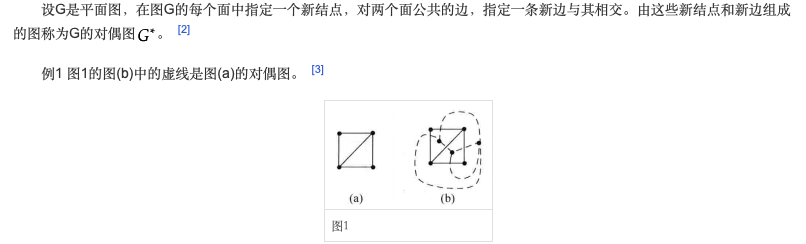
平面图的定义:能在平面上画出没有相交的边的图,称为平面图(planar)
针对平面图而言的面(faces):
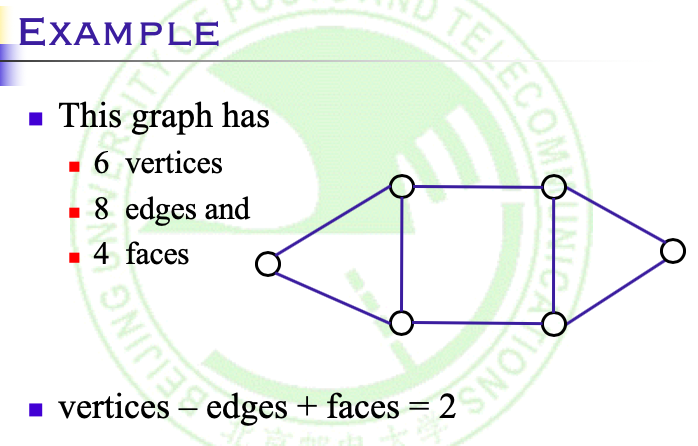
欧拉定理:
令G是一个连通的平面简单图,那么有:
\(V-E+F=2\)或\(V-E+R=2\)
==》R = E-V+2其实就算G具有重边或自环的平面图也成立
定理1:
具有n个顶点的简单图G,最多有3n-6条边
证明:
推论:
- 如果G是连通平面简单图,那么G中至少有一个顶点的度不超过5
- 如果G是连通平面简单图,并且v≥3且没有长为3的环,那么e≤2v-4
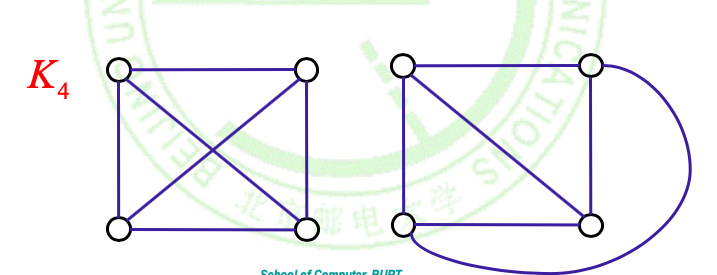
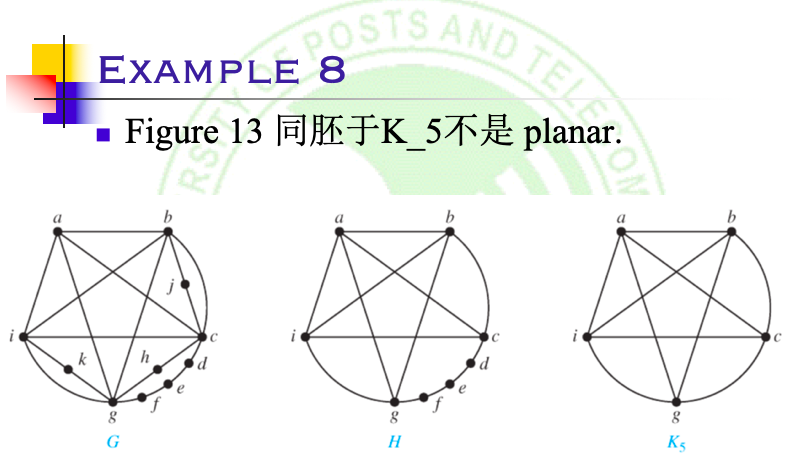
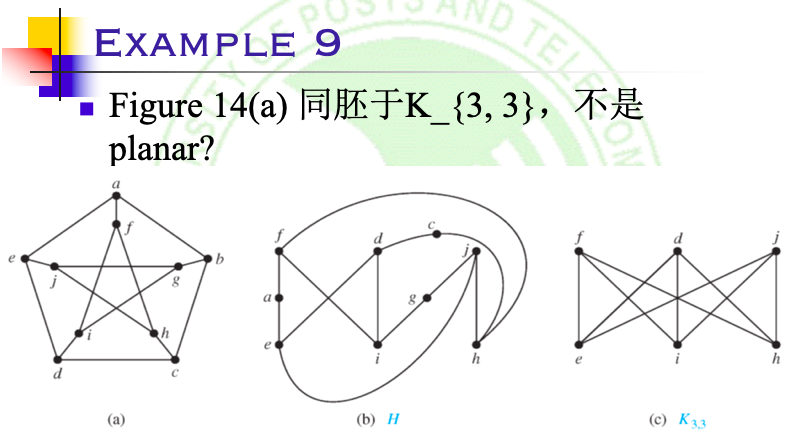
通过以上分析:\(K_5\)和\(K_{3, 3}\)都不是平面图
库拉托夫斯基定理(Kuratowski’s Theorem)
定理内容:证明一个图是平面图的必要充分条件是 它不包含任何同胚于\(K_5\)或\(K_{3, 3}\)的子图
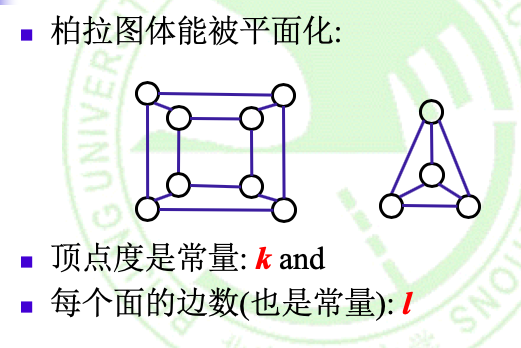
柏拉图体
柏拉图体的平面化:
推论: