10.2图的一些术语(Graph Terminology)
10.2图的一些术语(Graph Terminology)
- 相邻(Adjacency):
无向图G中的一边e连接u,v,那么我们称u和v是相邻/连通(adjacent / neighbors / connected)的;其中也称u和v是边e的端点(endpoints)
- 领域(Neighborhood)
与顶点v相邻的所有点的集合N(v)称为v的领域(neighborhood of v);顶点集合A的领域指的是其内所有点领域的交集
- 度(degree)
顶点v的度,记作deg(v),等于入度(in-degree)和出度(out-degree)的和;度为0的点称为孤立点;度为1的点称为悬挂点(pendant)
- 握手定理(Handshaking Theorem)
无向图中,如果有度为奇数的点,那么这些点的个数必为偶数个
- 有向图中的相邻
e映射到(u, v),称之为u通过e邻接到v;u是e的初始点(initial vertex),v是e的终点(terminal vertex )
常用\(deg^-(v)\)表示v的入度, \(deg^+(v)\)表示v的出度
一些特殊的图的结构
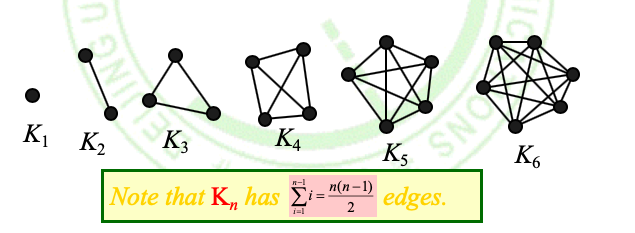
完全图(Complete graphs)
n阶完全图记为\(K_n\)
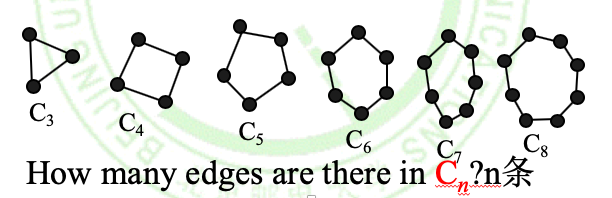
环图(Cycles)
n阶环图记为\(C_n\)
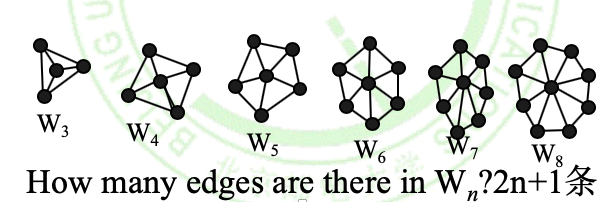
车轮图(Wheels)
n阶车轮图记为\(W_n\)
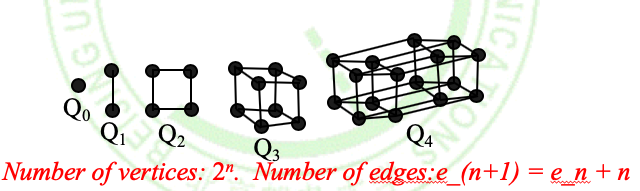
n维体图(n-cubes/hypercubes)
n维体图记为\(Q_n\)
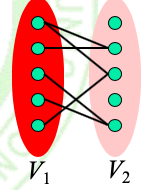
二部图/二分图(Bipartite Graphs)
顶点能被分为两个集合,使得任意一个集合中的点没有边直接相连
用\(K_{m,n}\)记作两个部分分别为m和n个顶点的完全二分图
用邻接矩阵表示的话,结果是一个上三角/下三角矩阵

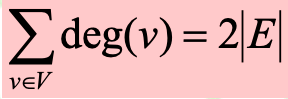
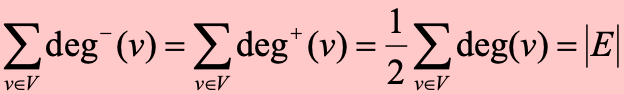


 浙公网安备 33010602011771号
浙公网安备 33010602011771号