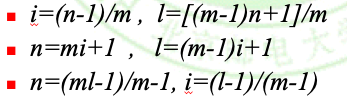11.1树(TREES)
11.1树(TREES)
树的特点:
- 树是一个无向无环图，任意两个节点间都有唯一的一个简单路径
- 一系列树组成森林(forest)
- 树或森林的叶子节点指悬挂点(pendant)或孤立顶点(isolated vertex)
- 内部顶点(internal node)的度≥2
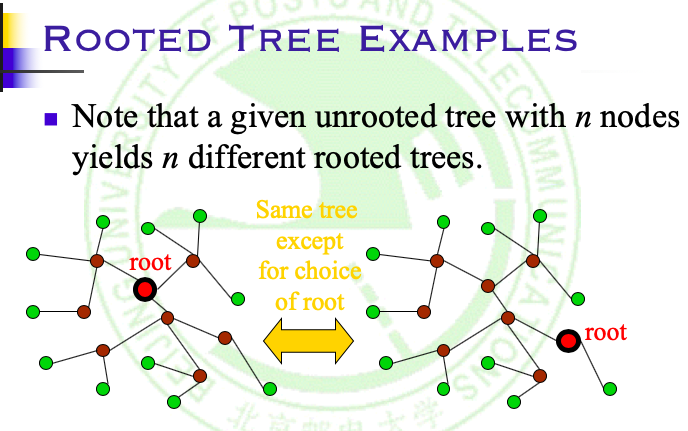
有根树(Rooted Trees)
- 有根的树称为有根树
- 有根树中的一些术语:
父母； 孩子； 兄弟姐妹(siblings)； 祖先(ancestors)； 后代(descendents)； 叶子； 内部节点(internal node)； 子树...
- 根若有，可能不唯一
n叉树(N-ary Trees)
定义一颗有根树中任何一个节点都不超过n个孩子节点的树为n叉树；贴别的，2-ary tree也称为binary tree.
有序有根树(Ordered Rooted Tree)
孩子节点有序排列的有根树称为有序有根树(如左孩子，右孩子等等)
一些树模型
图书管理信息，族谱等，具体例略
一些树的定理
- n个节点的树有e=n-1条边
- 满m叉树如果有i个内部节点，则有n=mi+1个节点，有l=(m-1)i+1个叶子节点(提示:l=n-i)
- 对于一颗满m叉树，边树e，内部节点数i，节点总数n和叶子节点数l这4者知其一则另外3个都能得知，具体关系如下:
- 高为h(只有根节点默认高度为1)的m叉树最多有\(m^h-1\)个节点，最少有h个节点
