最小生成树：Prim算法和Kruskal算法

最小生成树：Prim算法和Kruskal算法

一、什么是最小生成树？

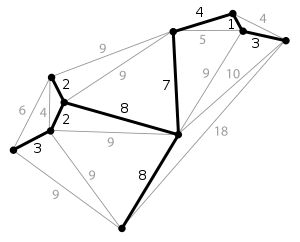
最小生成树是一副连通加权无向图中一棵权值最小的生成树。
如:

二、Prim算法和Kruskal算法的原理

Prim算法原理：

1）以某一个点开始，寻找当前该点可以访问的所有的边；
2）在已经寻找的边中发现最小边，这个边必须有一个点还没有访问过，将还没有访问的点加入我们的集合，并记录添加的边；
3）寻找当前集合可以访问的所有边，重复(2)的过程，直到没有新的点可以加入；
4）此时由所有边构成的树即为最小生成树。

Kruskal算法原理：

1）将边按权从小到大进行排序；
2）依次进行加边操作:如果新加的边连接两个互不联通的点，那么就把边连接上并更新连通性(这里建议运用并查集数据结构来维护)，否则忽略该边
3）重复(2)的过程，直到所有点都连通(或者加了n-1条边)；
4）此时由所有边构成的树即为最小生成树。

总之，Prim算法以点为对象不断更新集合来构成最小生成树；Kruskal算法则是以边为对象不断更新集合来得到最小生成树。破边法和Kruskal算法内核一致，只是操作刚好相反，此不赘述。(对于一个稠密图，prim算法要优于Kruskal算法，但是Kruskal更好写啊QAQ)

实战1:Prim

暂时空缺

实战2:Kruskal

P2212浇地

思路:先生成完全图，然后生成最小生成树，鉴于该题要求选的边不小于C,因此选用Kruskal算法直接忽略不符合的边即可

赋AC代码(用到并查集模板)：

#include <stdio.h>
#include <stdlib.h>
#define MAXN 2000
int fa[MAXN+1];
typedef struct maye
{
    int x, y;
}ccc;
typedef struct mayeye
{
    int u, v, l;
}ddd;
void init(int n)
{
    for(int i = 1; i <= n; i++)
    {
        fa[i] = i; //初始化
    }
}

int find(int x)
{
    if(fa[x]==x)
        return x;
    return fa[x] = find(fa[x]); //查询时进行路径压缩
}

void merge(int x, int y)
{
    fa[find(x)] = find(y); //合并
}

int com(const void *a, const void *b)
{
    return (*(ddd *)a).l - (*(ddd *)b).l;
}

int main(void)
{
    int n, c;
    scanf("%d %d",&n,&c);
    ccc dot[n+1];
    for(int i = 1; i <= n; i++)
    {
        scanf("%d %d",&dot[i].x, &dot[i].y);
    }
    int m = n*(n-1)/2, t = 1;
    ddd arc[m+1];
    for(int i = 1; i <= n; i++) //按题要求生成所有边
    {
        for(int j = i+1; j <= n; j++)
        {
            arc[t].u = i;
            arc[t].v = j;
            arc[t].l = (dot[i].x - dot[j].x)*(dot[i].x - dot[j].x)+(dot[i].y - dot[j].y)*(dot[i].y - dot[j].y);
            t++;
        }
    }
    //Kruskal
    qsort(arc+1, m, sizeof(ddd), com); //将边按权排序
    init(n);
    int ans = 0, answer = 0;
    for(int i = 1; i <= m; i++)
    {
        if(arc[i].l<c)
            continue;
        if(find(arc[i].u)!=find(arc[i].v)) //符合情况选边
        {
            answer+=arc[i].l;
            ans++;
            merge(arc[i].u, arc[i].v);
        }
        if(ans==n-1)  //得到最小生成树就输出答案
        {
            printf("%d\n",answer);
            return 0;
        }
    }
    printf("-1\n");
    return 0;
}