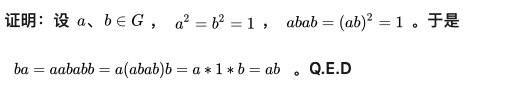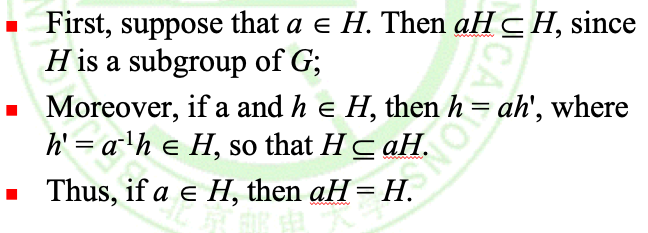10.3群,群直积,商群
群,群直积,商群
群(Groups)
如果独异点(G, *)中的每个元素均存在逆元(必定是唯一的),那么它便升级为群
集合S + 二元运算(自带封闭性) -> \((G, *)\),如果\((G, *)\)满足结合律,那么\((G, *)\)升级为半群 -> \((G, *)\)存在单位元e(必定是唯一的),那么\((G, *)\)升级为独异点 -> \((G, *)\)中每个元素存在逆元(必定是唯一的),那么\((G, *)\)升级为群
阿贝尔群(Abelian)
群G中任意两个元素a,b∈G,均满足阿贝尔律(交换律):ab = ba,那么群G升级为阿贝尔群
如:证明(G, *)是阿贝尔群
- 证明*对于G是一个二元运算(证明封闭性)
- 证明结合律
- 找出单位元
- 找出逆元
- 证明交换律
定理1:
逆元存在必唯一(显然)
定理2:
群G具有消去律(Witt律),包括左消去律和右消去律
定理3:
群G中满足:
- \((a^{-1})^{-1} = a.\)
- \((ab)^{-1} = b^{-1}a^{-1}\)
定理4:
如果G是群,a,b是群G中的元素,那么:
方程\(ax = b\)只有G中的唯一解
方程\(ya = b\)只有G中的唯一解
有限群(Finte Group)
群G中元素如果是有限的,则称为有限群,其中G的元素称为G的阶(order),记为|G|
显然,有限群能通过乘法表表示,或者说能用乘法表表示的群都是有限群
一个重要的群--n次对称群
置换:
通过轮换概念,我们可以知道置换也是群(但没必要)
对称群(symmetric group on n letters)
对称群是指含置换群为子类的一类具体的有限群
对于集合X上的双射: f: X -> X(也就是置换)
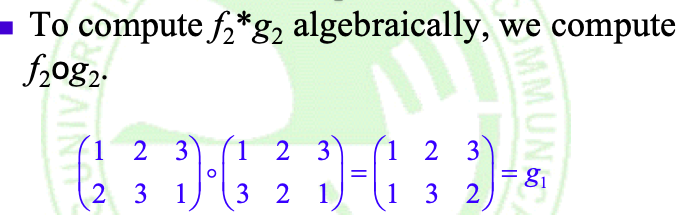
当X为有限集合时,置换的复合运算和(二元运算)部分置换操作(元素)构成了对称群,如:
下给出\(S_3\):
Note:n次对称群的阶为n!
子群(Subgroup)
令H是群G的一个子集,如果H满足群定义,那么H就是G的子群
\(H_1 = \{e\}, H_2 = G\)显然也是群,我们称这两个群为G的平凡子群(trivial subgroup)
G的生成群是除平凡子群外最简单的生成群(显然)
定理5:
设有群\((G, *)\)和群\((G', *')\),并且有同态映射f:G -> G',那么:
(a). 如果e是G的幺元,e'是G'的幺元,那么f(e) = e'
(b). 如果a∈G,那么\(f(a^{-1}) = (f(a))^{-1}\)
(c). 如果H是G的子群,那么f(H) = {f(h)|h∈H}也是G'的子群
Note:同构映射(isomorphism)会保持根据二元运算定义的所有性质(可以运用此性质来反证两个群不是同构)
如群\(S_3\)和\(Z_6\)都是阶为6的群,但前者不是Abelian,而后者是,故二者不同构
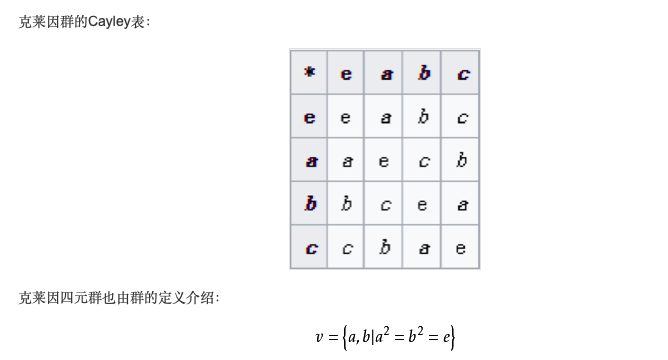
克莱因四元群(Klein 4 group)
表示:Klein = {e, a, b, ab};
克莱因群的所有元素都2阶的,克莱因四元群是最小的非循环群。然而,它又是一个阿贝尔群
循环群(cyclic group)
定义:循环群。由一个元素反复运算生成的群\(G = \{a^n | n ∈ Z \}\)称为循环群,简记为\(<a>\),a称为这个循环群的生成元。
Note:
- 循环群都是阿贝尔群,并且循环群的任意子群也是阿贝尔群
- 循环群G中的任意元素都是G或G的子群A的生成元。
- 群G的元素a的阶,是指由元素a生成的G的生成子群的阶,有:若群G中每一个非幺元素的阶均为2,则G是Abel群
- Lagrange定理:设G为有限群,则G中每个元素g的阶均是|G|的因子;若G有子群,则任意子群A的阶都是|G|的因子。
- p(素数)阶群G均是Abel群,并且同构于\(Z_p\)。
- 可见,4阶群都是Abel群
群直积和商群(Products and Quotients of Groups)
定理1:群直积
由群\(G_1和群G_2\)的乘积得到的群是群直积,且定义为:
\((a_1, b_1)(a_2, b_2) = (a_1a_2, b_1b_2)\)
证明和半群直积证明类似
设群\(G_1和群G_2\)都是mod2加法群\(Z_2\)(假设我们令0和1来表示等价类[0]和[1]),那么其乘积群G的乘法表如下:
如果我们通过如下定义函数,可以得到乘积群G和V/\(Z_4\)(唯二阶为4的群)同构:
NOTE
更一般的,我们可以得到如下:
定理2:商群
和商半群类似,通过定义在群G上的同余关系R和二元运算 口,我们能得到商半群(G/R, 口), 其中二元运算 口 被定义为:
- [a] 口 [b] = [a*b]
只需证明其有逆元即可
推论1:
显然函数\(f_R(a) = [a]:G -> G/R\)是一个群同态
推论2:
同态基本定理对群是同样适用的
陪集(coset)
定义:设H是群G的一个子集,a∈G,则集合aH(Ha)称为由a所确定的H在G中的左配集(右陪集),简称为H关于a的左陪集(右陪集),元素a称为陪集aH(Ha)的代表元素。
如果对于任何a∈G,均有aH = Ha,那么子群H称为G的正规子群
Waring:Ha = aH并不代表对于所有的h∈H,ha=ah均成立
意思是存在h,h'∈H,使得ha = ah'
如果H是G的子群,那么如果元素a∈H,就有:aH = H
证明:
EXP(求全部元素关于子群H的左陪集):
Note:1.由这个例子,我们可以清晰的看到:对于任意a,b∈G,要么aH = bH,要么aH ∩ bH = ∅ (右陪集同理) ==》 通过子群H,我们就像同余关系一样对G中的元素进行了划分,那么我们可以以此为基础来构造商集
2.观察例子,我们能发现:任意元素x∈G,x一定∈xH,其实这是一个普适规律(可以拿来快速求陪集?)
定理3:
设R是群G上的同余关系,H = [e]显然是群G的一个子群,那么:
对于任意a∈G,均有:[a] = aH = Ha,即H是G的正规子群
通过定理3和推论1,我们可以通过正规子群N = [e]的所有陪集来进行构建商集,其中,二元运算定义为:
(aN)(bN) = [a] 口 [b] = [ab] = abN
同时有函数\(f_R: G -> G/R\),定义为:
\(f_R(a) = aN\)
显然,\(f_R\)是从G到G/R的同态,我们也经常写成G/N
定理4:
设G的正规子群N,设定义在G上的关系R:
- a R b 当且仅当 \(a^{-1}b\)∈ N
那么有:
(a). R是G上的同余关系
(b). N是在R关系中的等价类[e]
可见,群G上的同余关系,正规子群H和G -> G/R(或G')的同态映射是等价的
推论2:
设同态映射f:G -> G',那么f的核(kernel),记为ker(f),定义为:ker(f) = {a ∈ G|f(a) = e'},那么:
- ker(f)是G的正规子群
- 商群G/ker(f)和G'同构
EXP:
\(f: Z -> Z_n\)定义为:f(m) = [r], 其中r = m%n, 那么ker(f) = nZ