11.1群与编码
Groups and Coding(群与编码)
编码理论:通过引入冗余信息(检验位)来帮助检测和纠正错误
- 基础定义:

- 通过定义在mod2加法上的群B来定义群\(B^m\):

在信号传输通道(Transmission channel)中,可能会产生噪声(Noise),使得接收到错误的码字
编码函数(Encoding function)
- 选择一个双射(one-to-one and onto)函数e:\(B^m -> B^n(n>m)\):
- 那么e称作(m, n)编码函数,将\(B^m\)中的每个码字表示在\(B^n\)中;
- 如果\(b ∈ B^m\),那么e(b)称作代表b的代码字(code word)- 显然,如果在传输过程中没有噪音,那么对于任意传输方编码的x = e(b)∈\(B^n\),接收方收到的\(x_t = x\);又由于编码函数e已知,故可直接解码出信息b
- 但是,传输过程中发生错误很常见,如果在传输前后的代码字x的\(x_t\)存在k个位置不同,那么我们就说x=e(b)传输错误为k
差错检测(Error detect)
假设e:\(B^m -> B^n\)是一个(m, n)编码函数:
- 显然,如果x = e(b)在传输过程中传输错误为k,那么接收方收到的\(x_t\)就不是一个代码字(\(x_t!=x\), 无法直接解码为b)
- 对于\(x ∈ B^n\),我们称x中1的个数为x的权(weight),并记为:\(|x|\)
奇偶校验码(parity check code)和其他编码函数
定义奇偶校验编码函数(偶校验)e:\(B^m -> B^{m+1}\),且(\(b_{m+1} = (|b|\)&\(1)⊕0\)):
考虑一个(m, 3m)编码函数e:
下给出所有的对3位信息编码后的代码字:
显然,如果接收方收到的码字01111101,这不是代码字(code word),说明传输过程中发生了传输错误
海明距离(Hamming distance)
- 设x,y均是属于\(B^m\)的码字,我们定义x和y的海明距离(Hamming distance)\(θ(x, y) = |x⊕y|\),即x⊕y的权(weight)
- x和y的海明距离的直观表述是:码字x和y中对应位不同的位置的个数,也称为码距(distance)
关于海明距离的一些性质:
note:(d)的证明利用了⊕运算的结合律
最小距离(Minimum distance)
编码函数e:\(B^m -> B^n\)的最小距离,是指任意两个代码字(code word)的距离的最小值,也就是
min{ \(θ(e(x), e(y)) | x, y ∈ B^m\)}
定理:(m, n)编码函数能检测k或更少的错误 \(<==>\) 该编码函数的最小距离\(>=\) k+1
群编码(Group Codes)
如果(m, n)编码函数e:\(B^m -> B^n\)满足:\(e(B^m) = \{ e(b) | e(b) ∈ B^n \}\) ,并且有,\(e(B^m)\)是\(B^n\)的子群,那么我们称e为群码(Group Codes)
exp:
note:求出N = \(e(B^m)\),再判断是否为\(B^n\)的子群(关于⊕的封闭性,单位元,逆元)
定理:假设e:\(B^m -> B^n\)是一个群码,那么:e的最小距离就是所有代码字的非零码字的权的最小值
证明:(最小距离肯定大于0-->因为不可能有两个码字编码后是一样的)
exp:
note:由上可见群码的好处
群编码(函数)的构造
布尔矩阵
- 定义矩阵异或运算(mod 2加法)😄 ⊕ E
- 定义矩阵布尔乘运算(mod 2布尔乘)😄 * E
那么可以有如下定理:⊕ 和 *对于矩阵具有分配律,即(D ⊕ E) * F = (D * F) ⊕ (E * F).
我们定义\(x = x_1x_2…x_n ∈ B_n\)为一个1×n的矩阵\([x_1 x_2 … x_n]\),我们得到如下定理:
如果\(0<m<n,r = n-m\),并且令H为一n×r的布尔矩阵,那么有:
- \(f_H:B^n -> B^r, 且f_H(x) = x*H,x∈B^n\) ,那么\(f_H\)是从群\(B^n\)到群\(B^r\)的一个同态
证明(⊕ 和 *的分配律):
推论1:
设\(m,n,r,H和f_H是刚刚推论中定义的\),那我们可以得到如下信息:
- \(N = \{x ∈ B^n | x * H = 0\}是B^n的一个正规子群\)
证明:
\(N是同态f_H的核(kernel), 故N是B^n的一个正规子群\)
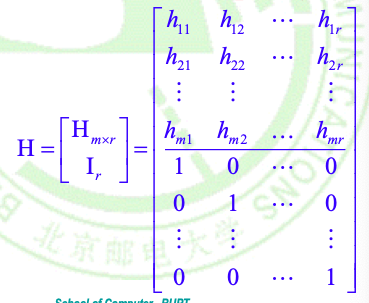
一致性检验矩阵(Parity check matrix)
定义:\(令m<n,r=n-m,那么下面这个n×r的布尔矩阵称为\)一致性检验矩阵:
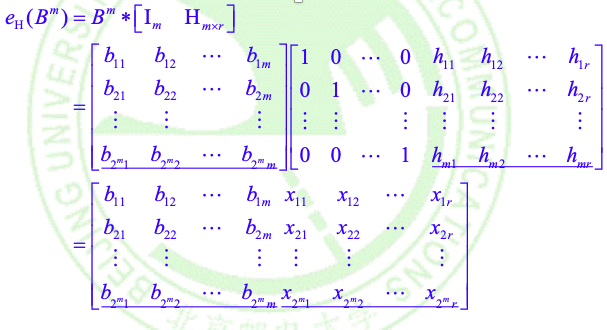
- 定义编码函数\(e_H:B^m -> B^n\):
\(b_{1×m} = b_1b_2...b_m\)
\(那么代码字x_{1×n}=e_H(b)=b_1b_2...b_mx_1x_2...x_r=b_{1×m}x_{1×r}\),其中:
- 完整矩阵表达形式:
最后的定理:
- 充分性:
- 必要性:
推论2(即其证明):
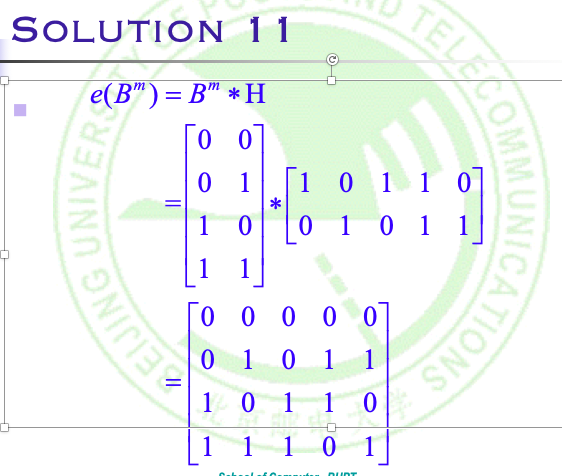
EXP:
Note:可见,如果有了一致检验性矩阵,我们可以通过右乘\([I_{m×m} H_{m×r}]\)来实现\(B^m -> B^n\)的群编码,同时也能通过右乘\(\begin{bmatrix} H_{m×r} \\ I_{r×R} \end{bmatrix}\)得到的结果是否为 0 来判断传输过程中是否发生错误


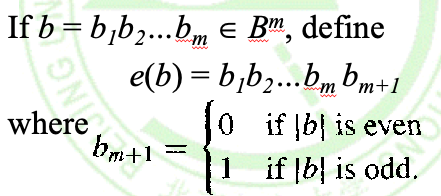
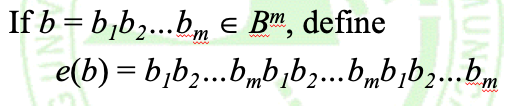










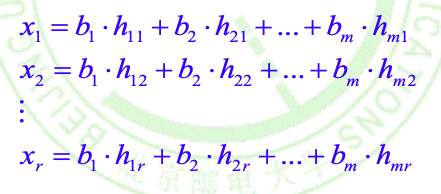








 浙公网安备 33010602011771号
浙公网安备 33010602011771号