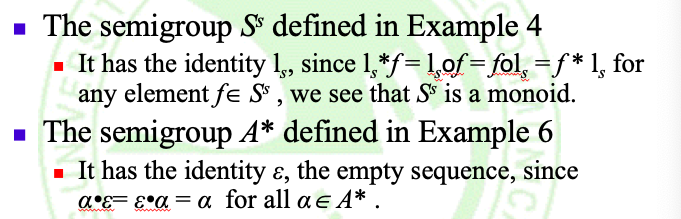10.2半群，同余关系，半群直积，商半群

半群与群(Semigroups and Groups)

半群(Semigroup)

非空集合S 和定义在集合S上的具有结合律(封闭性显然)的二元运算\(*\)组成了一个半群(S, *);

通常记为(S, *)或者S

a*b称为a和b的积

如果\(*\)具有交换律，那么(S, *)称为交换半群(阿贝尔半群)

如:(Z, +); (P(S), ∪)； (Z, -)...
Note:P(S)指的是S的全集，如S={1, 2, 3},那么P(S) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}

一些半群的例子:

设\(S^S\)为所有从函数f:S -> S的集合，定义f*g = fog(即复合函数)

*是定义在\(S^S\)的二元运算

*具有结合律

(\(S^S\), *)是一个半群

半群\(S^S\)不是交换群(无交换律)

设(L, ≤)是一个格(lattice), 和定义在L上的二元运算*:

a*b = a∪b

(L, *)是一个半群

操作符·是指连接运算，显然其具有结合律

称(\(A^*, ·\))为由A生成的自由半群(free semigroup generated by A)

定理1:

半群的卡特兰律(结合律)

单位元

单位元若存在，则必唯一

独异点(Monoid)，含幺半群

半群(S, *)中存在单位元，则称为独异点

之前例子中的半群\((S^S, *), (A^*, *)\)等均为独异点

子半群(Subsemigroup)

T是S的子集，并且(T, *)同样满足半群定义

子独异点(Submonoid)

T是S的子集，并且(T, *)同样满足独异点定义，同时e∈T

显然，半群\((S, *)\)本身也是S的子半群；独异点\((S, *)\)本身也是S的子独异点；
T = {e} 一定是群\((S, *)\)的子独异点

幂(Powers)

运算的幂通过如下定义:

生成子群和生成子独异点(由一个元素生成的子半群/子独异点)

同构映射(Isomorphism)

设有两个半群\((S, *)和(T, *^{'})\)
设有函数\(f: S -> T\)
如果

f是从S->T的一一对应(双射)的函数

对任意a，b∈S, 均有\(f(a*b) = f(a)*^{'}f(b)\)

则称f是从S到T的同构映射，简称同构

Note:如果f是从S->T的同构，即f是从S->T的一一对应的函数，那么\(f^{-1}\)必定存在，并且\(f^{-1}\)是从T->S的一一对应的函数(并且一定是同构，下证)

构造同构/判断是否为同构的一般步骤:

(构造或直接给出)构造一个函数\(f:S -> T\),使得f的定义域Dom(f) = S;

证明f是单射(one-to-one)的，可用反证法

证明f是满射(onto)的 --> 故而是双射的

证明\(f(a*b) = f(a)*^{'}f(b)\)
EXP:证明(Z, +) -> (T, +)，其中Z是整数集，T是偶数集

定理2:

如果S和T是独异点，且幺元分别为\(e，e^{'}\),并且存在\(f:S->T\)是从S到T的同构映射，那么:

\(f(e) = e^{'}\)

Note:显然，如果\((S, *)\)有独异点，但\((T, *^{'})\)没有独异点，那么必定不存在从S->T的同构(常用于证明不存在同构)

同态映射(Homomorphism)

设有两个半群\((S, *)和(T, *^{'})\)
设有函数\(f: S -> T\)
如果

对任意a，b∈S, 均有\(f(a*b) = f(a)*^{'}f(b)\)
则称f是从S到T的同态映射，简称同态

Note:同构和同态均满足：像点的乘积等于乘积的像点

定理3:

如果S和T是独异点，且幺元分别为\(e，e^{'}\),并且存在\(f:S->T\)是从S到T的满同态映射，那么:

\(f(e) = e^{'}\)

f必须是满同态才行，因为假如T中有个元素a没被映射，你凭啥说e'a＝a?

定理4:

如果S和T是半群,并且存在\(f:S->T\)是从S到T的同态映射，并且假设\(S^{'}\)是(S, *)的子半群，那么:

\(S^{'}的像f(S^{'})也是(T, *^{'})\)的子半群

证明如下:

定理5:

如果S是交换半群,T是半群,并且存在\(f:S->T\)是从S到T的满同态映射，那么:

\((T, *^{'})\)也是交换半群

这里同样要求满同态
证明如下:

半群直积和商半群(Products and Quotients of Semigroups)

定理1:

两个半群的笛卡尔乘积也是半群

\((S, *)和(T, *^{'})是半群，它们的笛卡尔乘积(S×T, *^{''})也是半群，其中二元运算*^{''}定义为: (s_1, t_1)*^{''}(s_2, t_2) = (s_1*s_2, t_1*^{'}t_2)\)

同样的，两个独异点的笛卡尔乘积也是独异点且其幺元为\((e_S, e_T)\)

同余关系(Congruence relation)

定义在群\((S, *)\)上的等价关系R，如果满足:

任意a R a' 并且 b R b' ==> \((a*b) R (a'*b')\)

那么我们说R是同余关系

Note:在S中等价于一个关系的所有元素则被划分为一个等价类,对于代数结构(群)也是如此

我们让[a] = R(a)来表示包含元素a的等价类

S/R表示所有等价类的集合

定理2:

令R是定义在半群(S, *)上的同余关系R
下定义关系口 :

其中, 口([a], [b]) = [a] 口 [b] = [a*b],显然口是从\(S/R×S/R -> S/R\) 的一个函数

(S/R，口)是一个半群,并且S/R称为商半群(quotient semigroup或者factor semigroup)
因为口对于S/R是一个二元运算并且满足结合律

推论:

如果(S, *)是独异点，那么(S/R, 口)也是独异点(商独异点？)，其幺元为[e]

定理3:

令R为定义在半群(S, *)上的同余关系，(S/R 口)是相应的商半群，那么下面这个函数:

是一个满同态(onto homomorphism)，也称为自然同态(natural homomorphism)
证明如下:

同态基本定理(Fundamental Homomorphism Theorem)

定理内容:

设f:S -> T是半群\((S, *)\)到半群(T, *')的一个同态，设R是定义在S上的一个关系且定义为对于S中的任意a和b，a R b 当且仅当 f(a) = f(b),那么:

(a). R是一个同余关系

(b). (T, *')和商半群(S/R, 口)是同构的

1.证明R是同余关系(congruence relation)