9.4 关系的闭包
9.4 关系的闭包
闭包的定义:
>关系R对于性质P的闭包,是加入最小数量的序偶,使得R恰好符合性质P所得到的集合 >R的闭包R1具有如下3个特点: >①. R1 包含 R >②. R1具有性质P >③. 如果R2具有性质P且R2包含R, 那么R2包含R1就R的有向图而言:
- 找其自反闭包(reflexive closure)
添加循环/闭环
- 找其对称闭包(symmetric closure)
沿相反方向添加弧线(箭头)
- 找其传递闭包(transitive closure)
如果a到b连通, 那么就添加从a到b的弧线(箭头)
自反闭包(reflexive closure)
定理:R是定义在A上的关系,那么R的自反闭包r(R) = R∪△
如何获得?
①. 在R的有向图的所有顶点上添加闭环
②. 令R的邻接矩阵的对角线上全为1
对称闭包(symmetric closure)
定理①:R是定义在A上的关系,那么R的对称闭包s(R) = R∪R-1
NOTE: R-1 = {(b, a) | (a, b) ∈ R}
NOTE: R-1的邻接矩阵是R的邻接矩阵的转置,
即: MRT = MR-1
定理②:R是对称的,当且仅当 R = R-1
NOTE:在对称关系的有向图中,用无向的边来代替弧线(箭头)
路径(Paths)
假设R为定义在A上的关系,则R从a到b,长度为n的路径可表示为以a为起始点,b为终点的一个有限序列π:
a, x1, x2, ..., xn-1, b;
其中,满足:a R x1, x1 R x2, ..., xn-1 R b
例:
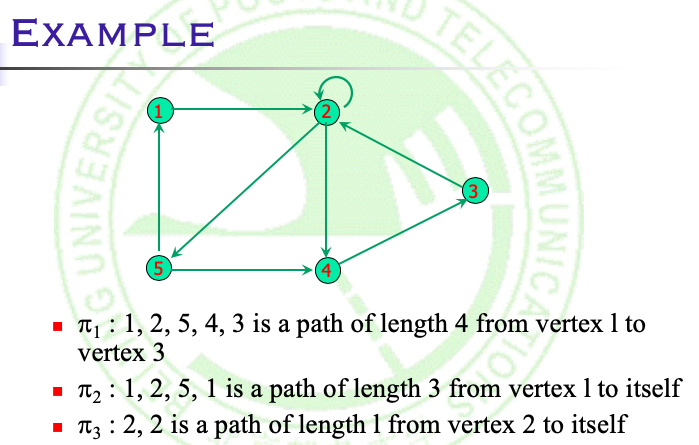
一些重要定义:
- 环(cycle):
一条起始点和终点为相同顶点的路径称为:环(cycle)
- Rn:
x Rn y表示,在R中存在一条或多条从x到y的路径
- 连通关系(connectivity relation) R*
R*包含的序偶对(a, b), 其中在R中至少存在一条从a到b的路径
例:

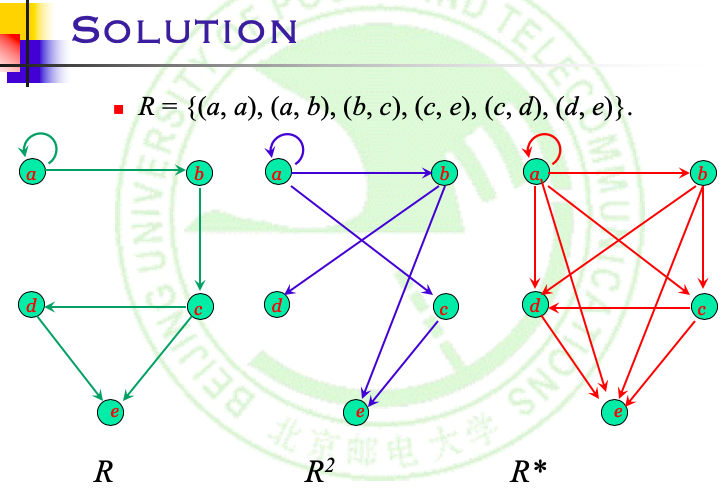
一些重要定理:
- 如果R是定义在A上的关系,那么有:
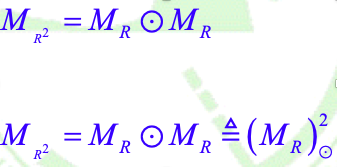
其中,⊙表示矩阵布尔乘法
证明:

- 当n>=2时,有:
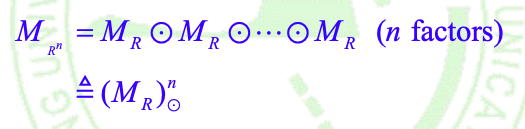
证明:科学归纳法(略)
连通关系(The connectivity relation)
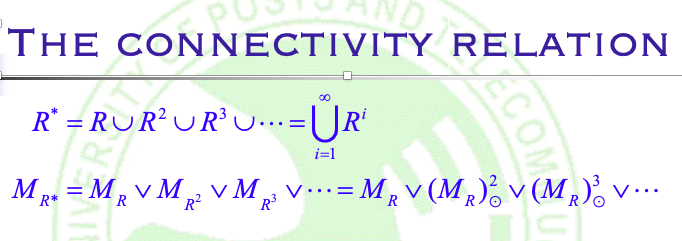
准备
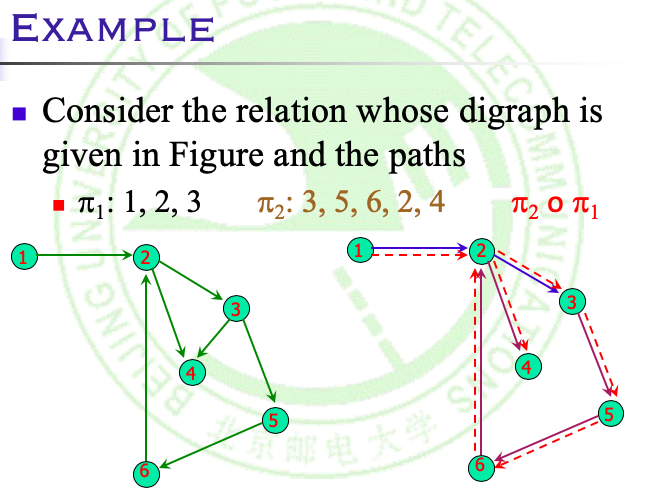
- 路径的合成
令:
π1: a, x1, x2, … , xn-1, b
π2: b, y1, y2, … , ym-1, c
则π1与π2合成后的路径为:
π2 o π1:a, x1, x2, … , xn-1, b, y1, y2, … , ym-, cNOTE THE ORDER!!!(注意顺序)
- 传递闭包(Transitive closure)
①. 关系R的传递闭包是包含R的最小的传递关系。
②. R是传递的, 当且仅当,对于任何的n,均有Rn ⊆ R(结论来自9.1)
③. 如果传递闭包存在一条从x到y的路径,那么一定有从x直接到y的弧线(箭头)
- 传递闭包里有用的一些结论:
①. If A ⊆ B and C ⊆ B, then (A∪C) ⊆ B.
②. If R ⊆ S and T ⊆ U then (RoT) ⊆ (SoU).
推论: If R ⊆ S then Rn ⊆ Sn
③. 如果R是传递的,那么Rn也是传递的
只需证明:(Rn)2 = (R2)n ⊂ Rn④. 如果对于j>k, 有Rk = Rj, 那么对于某些n>=j, 有Rj+m = Rn
除了Rj之外,我们无法得到任何新的关系
- 一个重要定理:
R为定义在A上的一个关系,那么R的闭包就等于R*

PROOF:我们必须证明,R∞
1). 是一个传递关系
2). 包含R
3). 是包含R的最小的传递关系
Proof of Part 1):
假设(x, y)和(y, z)都在R*中,只需证(x, z)也在R*中
由R*定义知,一定存在m,n,使得(x, y)和(y, z)分别在Rm和Rn中
又由复合定理,知:(x, z) ∈ RnoRm = Rm+n ⊆ R*
因此,R*是传递的
Proof of Part 2):
显然.
Proof of Part 3):

最重要的结论:
-
如果集合A的维数 = n,即|A|=n, 那么对于定义在A上的关系R,有:

-
等价命题:对于k<=n<=m,有1)和2)同时成立
- 1). Rm ⊆ Rk
- 2). (a, b) ⊆ Rm → (a, b) ⊆ Rk
证明其实就是去掉环,此处略
沃舍尔算法(Warshall’s Algorithm)
需要知道:内部顶点(Interior vertices)
大致方法:
①. 将n个节点赋予顺序为{a1, a2,…, an}, 并定义Wk = [tij]表示存在从第i个节点到第j个节点且仅通过内部节点{a1, a2,…, ak}这k个节点(这些节点可选可不选,但除此之外的节点都不能选)的路径连通,并记为“1”, 否则记为“0”
②. W0 = 初始邻接矩阵MR
③. 利用Wk-1来计算Wk
④. 得连通矩阵MR* = Wn
计算具体Wk的做法:
对于Wk中的tab
①. 如果Wk-1的sab == ‘1’,即仅利用{a1, a2,…, ak-1}这k-1个点(当然包括第a和第b个顶点)就能使a连通到b,那么Wk的tab直接 = ‘1’
②. 如果Wk-1的sab == ‘0’, 那么要使仅用{a1, a2,…, ak}这n个点从a连通到b, 则:
只需存在一个m(1 <= m <= k-1),使得在Wk-1中,有:sam == “1”并且smb == “1”(在Wk-1中,节点a到m连通,节点m到b连通, 那么在Wk中,节点a到b连通)
例:
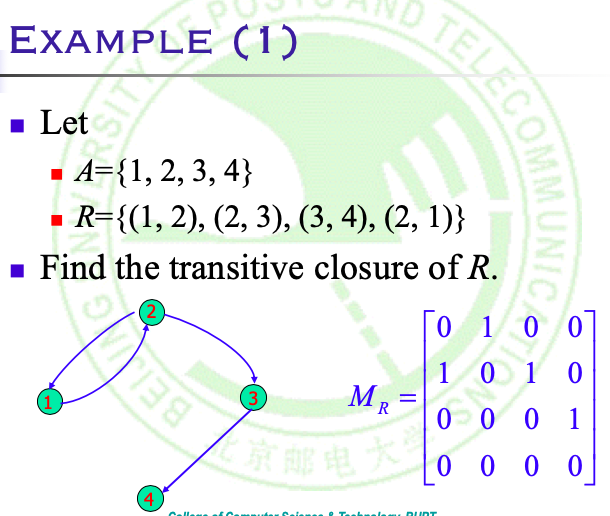
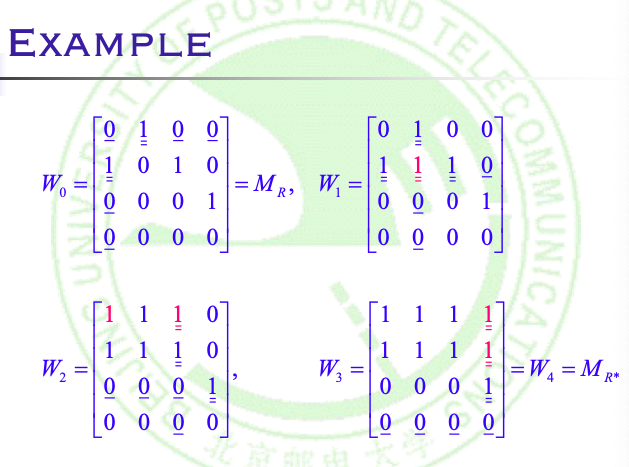
核心代码:
for(int k = 1; k <= N; k++)
{
for(int i = 1; i <= N; i++)
{
for(int j = 1; j <= N; j++)
{
if(W[k-1][i][j]=='1')
{
W[k][i][j] = 1;
}
else if(W[k-1][i][k]=='1'&&W[k-1][k][j]=='1')
{
W[k][i][j] = 1;
}
}
}
}
时间复杂度:O(n^3)
空间复杂度:O(n^3)
其实由于W[k]只与W[k-1]有关,可以只用二维数组来表示W[k-1],然后更新W[k]的时候直接覆盖到这个数组即可将空间复杂度压缩成O(n^2)
实战:Cow Contest

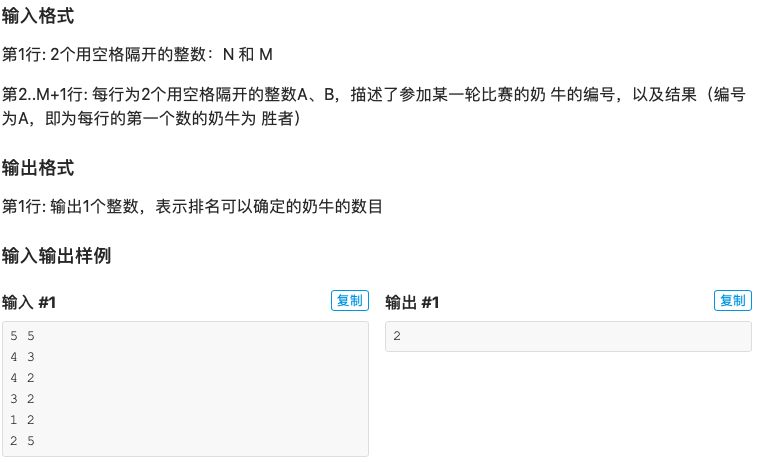
思路:只需求以这些牛组成有向图的传递闭包(用连通矩阵表示),再判断每个节点的入度+出度是否等于n-1,来判断每头牛能否确认排名
AC代码:
#include <stdio.h>
int main(void)
{
int n, m, a, b; //n头牛, m个关系
scanf("%d %d",&n,&m);
int W[n+1][n+1];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
W[i][j] = 0;
for(int i = 1; i <= m; i++)
{
scanf("%d %d",&a,&b);
W[a][b] = 1; //初始赋值W[0]
}
//这里即只需用一个二维数组表示W[k-1],然后将W[k]覆盖到W[k-1]这个二维数组上,使得空间复杂度为:O(n^2)
for(int k = 1; k <= n; k++)
{
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
//if(W[i][j]==1) // 代表第一种情况,完全可以省去
// W[i][j] = 1;
if(W[i][j]==0) //代表第二种情况
{
if(W[i][k]==1&&W[k][j]==1)
W[i][j] = 1;
}
}
}
}
int sumdu = 0, ans = 0;
for(int i = 1; i <= n; i++) //判断每个点的入度和出度之和是否为n-1
{
sumdu = 0;
for(int j = 1; j <= n; j++)
{
if(W[i][j]==1||W[j][i]==1)
sumdu++;
}
if(sumdu==n-1)
ans++;
}
printf("%d\n",ans);
return 0;
}
OTHERS
解决最短路径问题有几个常用的算法:
- ①. dijkstra算法,最经典的单源最短路径算法
- ②. bellman-ford算法,允许负权边的单源最短路径算法
- ③. spfa,其实是bellman-ford+队列优化,其实和bfs的关系更密一点
- ④. floyd算法,经典的多源最短路径算法
而Warshall算法和flody算法最具异曲同工之妙:
flody算法:用Wk的tab表示点a到点b只用{a1, a2,…, ak}这k个点和a与b所能达到的最短路径值,和Warshall算法一样,用W[k-1]来计算W[k],而Wn即为所有两点之间(即多源)最短路径的答案
- flody算法是用来求图的多源最短路径的算法,复杂度也为O(n^3)
- 将连通的边权定为有限值(如1),不连通的边权定为∞,便可以用flody算法求所有点的连通性(如i, j两个节点的最短路径为有限值即连通)
- Warshall算法和flody算法都能用动态规划的想法来理解:动态规划深刻理解flody
- 为什么 Dijkstra 不能提出 floyd 算法?因为他的名字是 ijk 而不是 kij



 浙公网安备 33010602011771号
浙公网安备 33010602011771号