9.1 关系及关系性质

9.1 Relations and Their Properties（关系及关系性质）

1.基本概念

- Ordered pair(序偶) 

当且仅当a<sub>1</sub> = a<sub>2</sub>并且b<sub>1</sub> = b<sub>2</sub>时， 才有序偶对(a<sub>1</sub>, b<sub>1</sub>)=(a<sub>2</sub>, b<sub>2</sub>)

• Cartesian product(笛卡尔积)
  
  如果A和B是两个非空集，我们将积集或笛卡尔积A×B定义为具有a∈A和b∈B的所有有序对（a，b）的集合
  A×B=

• m元笛卡尔积
  

• Partitions(划分)
  

  非空集A的划分（或称为商集）的集合P具有以下性质：

  1. A的每个元素属于P中的一个集合
  2. 如果A1和A2是P的不同元素，那么A₁∩A₂=∅

2.关系

定义：设A和B是非空集，那么从A到B的一个关系R就是A×B的一个子集， 并且有以下性质：

• 如果R属于A×B并且（a，b）∈R，我们就说a与b有关，写作：a R b。如果a与R无关，写作：a R b。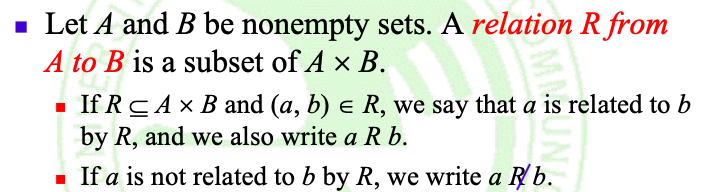

  通常，A和B是相等的。 在这种情况下，我们经常说R属于A×A是A上的关系。

一些例子：

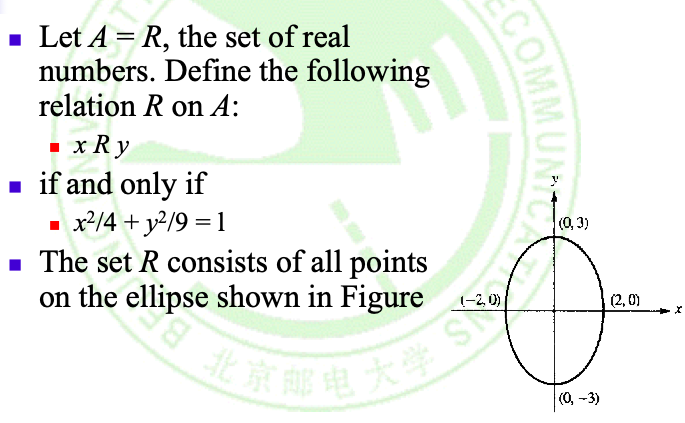
• 令R⊆A×B为A到B的一个关系， 则：

  1. Dom(R), R的定义域（domain）也是A的一个子集，并且是构成R的序偶中的所有第一个元素的集合。
  2. Ran(R), R的值域（range）是B中的元素集合，它们是R中对的第二元素。

• 若R⊆A×B为A到B的一个关系并且x∈A， 则：
  1.定义R(x)为所有满足x R y（x和y具有R关系）的B中所有y的集合

  • 即R(x) = { y∈B | x R y}.

一些Theorem（理论）

• 令R⊆A×B为A到B的一个关系，A₁,A₂是A的子集，那么有：
  

Proof of (a):

If y ∈ R(A₁)
then x R y for some x ∈ A₁.
Since A ₁ ⊆ A ₂, x ∈ A ₂.
Thus, y ∈ R(A₂)
Q.E.D.

Proof of (b):

Proof of (c):

Remark（备注）

证明技巧：Apply a relevant definition to a generic object.（将相关定义应用于通用对象。）即举反例。

• 设R和S均为A到B的关系，则：
  如果A中的所有a的R（a）= S（a），那么R = S.
  Proof:略

3.二元关系的特殊性质

给出全集U和U上的子集A的二元关系R,则有以下性质：

1. Reflexive(自反) and Irreflexive(反自反)
2. Symmetric(对称), Asymmetric(非对称), and Antisymmetric(反对称)
3. Transitive(传递)

Definition: [re]（自反的定义）

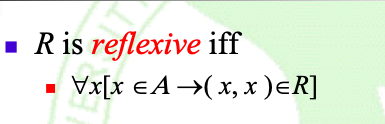
Note:

• 若A = ∅， 那么其也符合定义
• The void relation on a void Universe is reflexive!
  (全集U为∅时，空关系也是自反的)
• 如果U不是空的，那么自反关系中的所有顶点(vertices)都必须有环！

---

Definition : [ir]（反自反的定义）

Note:

• 若A = ∅， 那么其也符合定义
• 任何空关系都是反自反的！！！

---

Example1:

---

Definition: [Sy]（对称的定义）

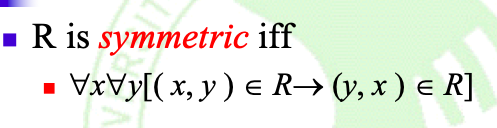
Note:

• 如果有arc（x，y），则必须有arc（y，x）

---

Definition: [As]（非对称的定义）

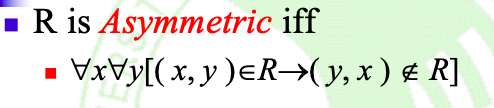
Note:

• 如果有arc（x，y），则一定不能有arc（y，x）

---

Definition: [Ats]（反对称的定义）

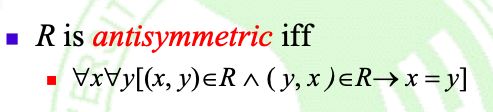
Note:

• 如果从x到y存在arc，则从y到x不能有一个弧arc
• 您应该能够富有逻辑地知道：如果（x，y）在R中并且x≠y，则（y，x）一定不在R中

---

Example2:

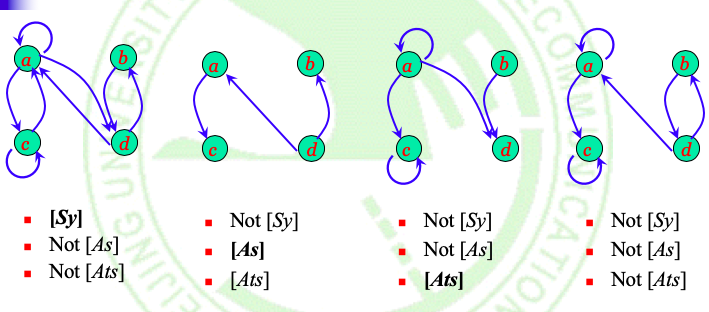
Note:

1. 对称和非对称不是矛盾对立关系(即存在既不是对称也不是非对称的关系) ；对称和反对称也不是矛盾对立关系。
2. 形式逻辑的定义：

• 【对称关系】：当aRb为真时,bRa必为真；
• 【反对称关系】；当aRb为真时,bRa必为假；
• 【非对称关系】；当aRb为真时,bRa有时真、有时假。

---

Definition: [tr]（传递的定义）

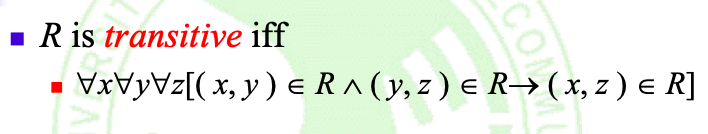
Note:

• 如果有一个从x到y的arc和一个从y到z的arc，则必须有一个从x到z的arc

---

Example3:

---

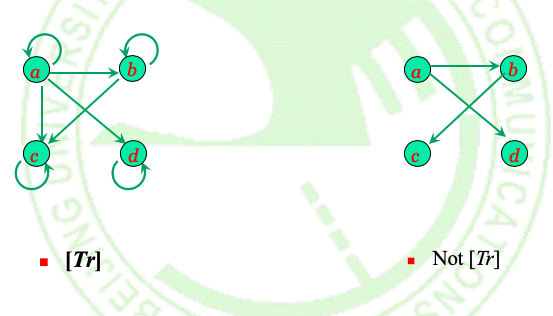
4.Combing relations(复合关系)

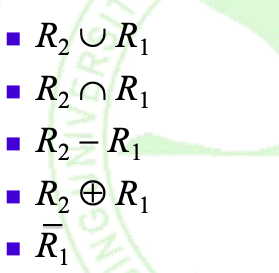
Note:R₁ ⊕ R₂ = (R₁-R₂) ∪ (R₂-R₁)

现设

• A，B，C均为集合
• R为A到B的关系
• S为B到C的关系

则The composition of R and S(R和S的复合关系)，记作SoR，定义为：

如果a∈A并且c∈C，那么有：a SoR c 当且仅当 存在b∈B，使得a R b and b S c.

复合定理：

设R是从A到B的关系，S是从B到C的关系。那么，如果A₁是A的子集，我们有:
(SoR)(A₁) = S(R(A₁))

证明如下：

关系的幂(power)

令R为A到A的关系，则Rⁿ,n=1,2,3…定义有：R¹=R and Rⁿ⁺¹=RⁿoR

关于“关系的幂”的一个定理：

A到A的关系R是transitive(传递的) <==> Rⁿ⊆R,n=1,2,3…

证明如下：

1. Proof: R transitive → Rⁿ ⊆ R

• 科学归纳法即可，不赘述

2. Proof: R_n ⊆ R → R transitive

Use the fact that R² ⊆ R
if (a, b) ∈ R and (b, c) ∈ R, then by the definition of composition, (a, c) ∈ R².
Because R² ⊆ R, this means that (a, c) ∈ R.
Hence, R is transitive.
Q.E.D.

---

OTHERS

1.一个「等价关系」需要满足：自反性，对称性和传递性，缺一不可。

2.如果一个二元关系集合P定义在一个n元素集合(设A={1，2，3......n})上，那么：

• 1.满足symmetric(对称)的集合个数为:2^n(n+1)/2个

P所有可能的元素为:

(1,1)	(1,2)	(1,3)	...	(1,n)
(2,1)	(2,2)	(2,3)	...	(2,n)
(3,1)	(3,2)	(3,3)	...	(3,n)
...	...	...	...	(3,n)
(n,1)	(n,2)	(n,3)	...	(n,n)

满足对称性定义的最小元素组:{(1,1)}, {(2,2)}, ......{(n,n)}这n个单元素集合和{(1,2), (2,1)}, ......{(n-1,n), (n, n-1)}这(nⁿ-n)/2个元素组

故：sum = 2^n+(n2-n)/2 = 2^n(n+1)/2个

• 2.满足antisymmetric(反对称)的集合个数为:2ⁿ * 3^n(n-1)/2个

P所有可能的元素为:

(1,1)	(1,2)	(1,3)	...	(1,n)
(2,1)	(2,2)	(2,3)	...	(2,n)
(3,1)	(3,2)	(3,3)	...	(3,n)
...	...	...	...	(3,n)
(n,1)	(n,2)	(n,3)	...	(n,n)

满足反对称定义的最小元素组:{(1,1)}, {(2,2)}, ......{(n,n)}共n个，(这些元素可选可不选，共2ⁿ种)
对于除了这些元素之外的其他元素，分为矩阵对角线的左下与左上，分别有2^n(n-1)/2个，对于特定的某个元素，如(a,b),a≠b,满足反对称定义的元素组有:{(a,b)}, {(b,a)}, {∅}共3种，故而这些元素一共有3^n(n-1)/2种选法

故：sum = 2ⁿ * 3^n(n-1)/2个

• 3.满足asymmetric(非对称)的集合个数为: 3^n(n-1)/2个

相比较②，区别在于对角线元素不能选，其余一致

故：sum = 3^n(n-1)/2个

• 4.满足irreflexive(反自反)的集合个数为:2^n(n-1)个

对角线元素不可选，其余nⁿ-n个元素无差别选取

故：sum = 2^n(n-1)个

• 5.满足reflexive(自反)同时symmetric(对称)的集合个数为:2^n(n-1)/2个

要满足自反，则对角线元素必须全取，同时要对称，则(a,b)和(b,a)组成一组元，可取可不取，共n(n-1)/2组

故: sum = 2^n(n-1)/2个

• 6.既不满足reflexive(自反)又不irreflexive(反自反)的集合个数为:2ⁿ²-2*2^n(n-1)个

P所有可能的元素为:

(1,1)	(1,2)	(1,3)	...	(1,n)
(2,1)	(2,2)	(2,3)	...	(2,n)
(3,1)	(3,2)	(3,3)	...	(3,n)
...	...	...	...	(3,n)
(n,1)	(n,2)	(n,3)	...	(n,n)

意味着对角线元素既不能全部取到，又不能全部不取
即：其补集为对角线元素全取或者全不取，总数为：2*2^n(n-1)个

故：sum = 2ⁿ²-2*2^n(n-1)个

摘自离散9.1的47