杂题集萃[6]
题目描述
给出一棵 \(N\) 个节点的树,树上的每个节点都有一个权值 \(A[i]\)。
有 \(Q\) 次询问,每次在树上选中两个点 \(u,v\),考虑所有在简单路径 \(u,v\) 上(包括 \(u,v\))的点构成的集合\(S\)。
求$$\sum_{w\in S}{A[w]orDist(u,w)}$$
其中 \(Dist(u,w)\) 为简单路径 \(u,w\)上的边数,\(or\)是按位或。
输入描述:
第一行两个整数 \(N,Q\)。
接下来一行 \(N\) 个整数,第 \(i\) 个为 \(A[i]\)。
接下来的 \(N−1\) 行,每行两个整数 \(u,v\)。表示 \(u,v\) 之间有一条边。
接下来的 \(Q\) 行,每行两个整数 \(u,v\)。表示一组询问。
输出描述:
一行一个整数,代表小N想知道的数的数量。
-
输入
5 2
4 3 2 5 3
1 2
1 3
3 4
3 5
2 5
3 4
-
输出
13
7
数据范围:
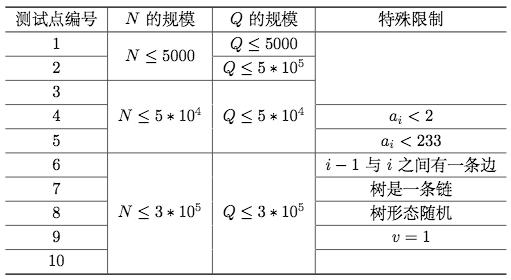 |
|---|
题解
算法 1
对于每组询问,遍历所有节点,看看它是不是在路径上,并计算答案。
时间复杂度 \(O(nq)\)。期望得分 \(10\) 分。
算法 2
由于可能询问的点对只有 \(O(n^2)\) 组,每次枚举 \(u\) 开始深搜。
时间复杂度 \(O(n^2)\)。期望得分 \(20\) 分。
算法 3
当树形态随机的时候,两个点之间期望只有 \(O(\log n)\) 个点,暴力即可。
时间复杂度 \(O(Hq)\)。期望得分 \(20\) 分,结合算法 2,期望得分 \(30\) 分。
算法 4
当 \(a_i<2\) 的时,按位或只会对最后一位产生影响,即,当 \(dist(w,u)\) 为奇数且 \(a_w=1\) 时,答案需要减 \(1\)。于是只要倍增时顺便维护从每一个点 \(t\) 出发,向上 \(2^i\) 的距离之内,与 \(t\) 距离为奇数且点权为 \(1\) 的点的个数就行了。
时间复杂度 \(O(n\log n)\)。期望得分 \(10\) 分,结合算法 2、3,期望得分 \(40\) 分。
算法 5
类似的,可以分别考虑每一个二进制位对答案的贡献。即,对于位 \(2^x\),维护从每一个点 \(t\) 出发,向上 \(2^i\) 的距离之内,与 \(t\) 距离为 \(d\) 满足 \(d \mathbin{\mathrm{and}} 2^x = 2^x\) 且点权的二进制表示中包含 \(2^x\) 的点的个数就行了。
由于路径有向上的部分,也有向下的部分,因此还需要维护满足 \(d \mathbin{\mathrm{and}} 2^x = 0\) 的点的个数在从 \(v\) 倍增的时候使用。
时间复杂度 \(O(n\log n \log a_i)\) 期望得分 \(50\) ~ \(60\) 分。
算法 6
注意到并不需要对于每一个位分别维护点的个数和,只需要维护所有重叠的位的数位和就行了,于是乎可以少掉一个 \(\log\)。
时间复杂度 \(O(n\log n)\) 期望得分 \(100\) 分。
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+7;
struct query{int x,y,id;}q[N];
int n,Q,lg,a[N],dep[N],fa[N][20],cnt[N][20];
ll fu[N][20],fd[N][20];
vector<int>G[N];
inline void dfs(int u){
for(int i=0;i<=lg;i++)cnt[u][i]=cnt[fa[u][0]][i]+!(a[u]&(1<<i));
for(int i=0;i<G[u].size();i++)
if(G[u][i]!=fa[u][0])fa[G[u][i]][0]=u,dep[G[u][i]]=dep[u]+1,dfs(G[u][i]);
}
inline int lca(int u,int v){
if(dep[u]<dep[v])swap(u,v);
int t=dep[u]-dep[v];
for(int i=lg;~i;i--)
if(t&(1<<i))u=fa[u][i];
if(u==v)return u;
for(int i=lg;~i;i--)
if(fa[u][i]!=fa[v][i])u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
inline ll query1(int u,int v){
ll ans=0;
int t=dep[u]-dep[v];
for(int i=lg;~i;i--)
if(t&(1<<i))
ans+=fu[u][i],u=fa[u][i],ans+=(1ll<<i)*(cnt[u][i]-cnt[v][i]);
return ans;
}
inline ll query2(int u,int d){
ll ans=0;int v=u;
for(int i=0;i<=lg;i++)
if(d&(1<<i))
ans+=fd[v][i]+(1ll<<i)*(cnt[u][i]-cnt[v][i]),v=fa[v][i];
return ans;
}
int main(){
scanf("%d%d",&n,&Q);
while((1<<lg)<n)lg++;
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1,x,y;i<n;i++)scanf("%d%d",&x,&y),G[x].push_back(y),G[y].push_back(x);
dep[1]=1;
dfs(1);
for(int i=1;i<=n;i++)fu[i][0]=fd[i][0]=a[i];
for(int j=1;j<=lg;j++)
for(int i=1;i<=n;i++){
fa[i][j]=fa[fa[i][j-1]][j-1];
fu[i][j]=fu[i][j-1]+fu[fa[i][j-1]][j-1]+(1ll<<j-1)*(cnt[fa[i][j-1]][j-1]-cnt[fa[i][j]][j-1]);
fd[i][j]=fd[i][j-1]+fd[fa[i][j-1]][j-1]+(1ll<<j-1)*(cnt[i][j-1]-cnt[fa[i][j-1]][j-1]);
}
while(Q--){
int x,y,f,d;
scanf("%d%d",&x,&y);
f=lca(x,y);
d=dep[x]+dep[y]-dep[f]*2;
printf("%lld\n",query1(x,fa[f][0])+query2(y,d+1)-query2(f,dep[x]-dep[f]+1));
}
}

