三角形的翻折问题

前言

这个类型的题目我迭代了三个版本，虽然得到的结论是一样的

第一个版本

如图，\(Rt\Delta ABC\) 中，\(AB=2,BC=1\)，\(D\) 是斜边 \(AC\) 上的动点，沿 \(BD\) 将 \(\Delta ABD\) 翻折到 \(\Delta A'BD\)，

使二面角 \(A'-BD-C\) 为直二面角，当线段 \(A'C\) 的长度最小时，四面体 \(A'BCD\) 的外接球的表面积为 \((B)\)

\(\large A.\frac{13\pi}{4}\) \(\large B.\frac{14\pi}{3}\) \(\large C.\frac{13\pi}{3}\) \(\large D.\frac{12\pi}{5}\)

我的想法就是设 \(\angle ABD= \theta\)，那么 \(\angle CBD=\frac{\pi}{2}-\theta\)

以 \(\angle ADB\) 是钝角为例，其它相同，作 \(AH\bot BD\)，那么 \(H\) 显然在线段 \(BD\) 外，\(AH=AB\sin \theta,BH=AB\cos \theta\)

那么通过余弦定理就可以算出 \(CH\) 的长，再结合直二面角用勾股定理就可以算出 \(AC\) 的长

\(CH=\sqrt{BH^2+BC^2-2BH\times BC\sin \theta},AC=\sqrt{AB^2+BC^2-AB\times BC\sin {2\theta}}\)

当 \(\theta=\frac{\pi}{4}\) 时，\(AC\) 取得最小值，此时 \(BD\) 是 \(\angle ABC\) 的角平分线

由于二面角是直二面角，那么外接球的圆心即是两个半平面过重心的法线的交点，

\(AD=2CD\)，则 \(AD=\frac{2\sqrt{5}}{3},CD=\frac{\sqrt{5}}{3}\)

\(\Delta ABD\) 外接圆半径为 \(\frac{AD\sin \angle ABD}{2}=\frac{\sqrt{10}}{3}\)，设其圆心为 \(O_1\)

\(\Delta CBD\) 外接圆半径为 \(\frac{CD\sin \angle CBD}{2}=\frac{\sqrt{10}}{6}\)，设其圆心为 \(O_2\)

\(\Delta ABC\) 面积为 \(\frac{1}{2}AB\times CB=\frac{1}{2}BD\times AB\sin \angle ABD+\frac{1}{2}BD\times BC\sin \angle CBD\)

那么 \(\large BD=\frac{\sqrt{2}AB\times BC}{AB+BC}=\frac{2\sqrt{2}}{3}\)，

\(O_1\) 到 \(BD\) 的距离为 \(\sqrt{(\frac{\sqrt{10}}{3})^2-(\frac{1}{2}\times \frac{2\sqrt{2}}{3})^2}=\frac{2\sqrt{2}}{3}\)

\(O_2\) 到 \(BD\) 的距离为 \(\sqrt{(\frac{\sqrt{10}}{6})^2-(\frac{1}{2}\times \frac{2\sqrt{2}}{3})^2}=\frac{\sqrt{2}}{6}\)

那么外接球半径为 \(\sqrt{(\frac{2\sqrt{2}}{3})^2+(\frac{\sqrt{2}}{6})^2+(\frac{1}{2}\times \frac{2\sqrt{2}}{3})^2}=\sqrt{\frac{7}{6}}\)

外接球表面积就是 \(4\pi (\sqrt{\frac{7}{6}})^2=\frac{14\pi}{3}\)

第二个版本

在 \(\Delta ABC\) 中，\(\angle BAC=\frac{\pi}{2}\)，\(AB=6,AC=8\)，\(D\) 是斜边上的一点，

以 \(AD\) 为棱折成二面角 \(C-AD-B\)，其大小为 \(\frac{\pi}{3}\)，则折后线段 \(BC\) 的最小值为 \((2\sqrt{7})\)

可以猜想，\(BC\) 最短当且仅当 \(AD\) 是 \(\angle BAC\) 的角平分线，当然，这是需要证明的，但是关键是这个二面角应该怎么弄。

首先可以发现，我们根本不需要关心 \(AB,AC\) 的具体边长，因为只需要求出折叠后的 \(\angle ABC\) 的余弦值即可。

\(BC=\sqrt{AB^2+AC^2-2AB\times AC\cos \angle BAC}\) 那么 \(\cos\angle BAC\) 最大时，\(BC\) 最小。

不妨直接手工造一个二面角出来。

那么可以通过 \(h_1,h_2\) 将绿色的边算出来，也即是 \({h_1}^2+{h_2}^2-2h_1\times h_2\cos \frac{\pi}{3}\)

而且 \(\large \frac{h_1}{\tan \alpha}=\frac{h_2}{\tan(\frac{\pi}{2}-\alpha)}=h_2\tan\alpha\)

再结合两条蓝边分别为 \(\large \frac{h_1}{\sin \alpha},\frac{h_2}{\cos\alpha}\)

通过余弦定理可以知道

\[\large \cos \angle BAC=\frac{(\frac{h_1}{\sin\alpha})^2+(\frac{h_2}{\cos \alpha})^2-{h_1}^2-{h_2}^2+h_1\times h_2}{2\frac{h_1}{\sin\alpha}\times \frac{h_2}{\cos\alpha}} \]

合并同类项，\(\frac{1}{\sin^2 \alpha}-1=\frac{1}{\tan^2\alpha},\frac{1}{\cos^2 \alpha}-1=\tan^2\alpha\)

由于 \(\frac{h_1}{\tan^2\alpha}=h_2\) 而且 \(h_2\tan ^2\alpha =h_1\)，所以分子其实是 \(3h_1\times h_2\)

那么 \(\large \cos \angle BAC=\frac{3}{2}\sin\alpha\cos\alpha=\frac{3}{4}\sin 2\alpha\)

恰好 \(\alpha\) 取 \(\frac{\pi}{4}\) 时 \(BC\) 最小，为 \(\sqrt{6^2+8^2-2\times 6\times 8\times \frac{3}{4}}=2\sqrt{7}\)

其实初代的第二个版本化简式子化简成一个基本不等式的式子了，现在重推的会简单一点，可以认为是2.5版本。

第三个版本

就是说，如果 \(\angle BAC\) 不一定是一个直角，是一个锐角或者钝角，那么还满不满足角平分线时最短的性质，当然猜想是同样成立的。

为了方便起见，其实 \(h_1,h_2\) 可以化成交线的边长 \(h\)，并且根本不关心具体边长，只求出新的 \(\cos \angle BAC\)，

设折叠前 \(\angle BAC=\beta\)，二面角的大小为 \(\gamma\)，仍然设折叠后其中一角为 \(\alpha\)

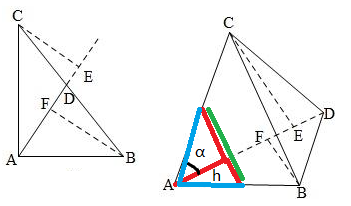
但是有一个很大的问题就是如果 \(\alpha\) 或者 \(\beta-\alpha\) 为 \(\frac{\pi}{2}\)，那就不能同上手工弄出一个二面角，不妨将其单独考虑。

这里以 \(\alpha=\frac{\pi}{2}\) 为例，如果是锐二面角的话，点 \(C\) 的投影就会在里面，钝二面角就在外面。（下式相当于是竖坐标和垂足到点 \(B\) 的距离用一次勾股定理）

\[BC=\sqrt{(AC\sin \gamma)^2+[(AB\cos (\pi-\beta)-AC\cos \gamma)^2+(AB\sin (\pi-\beta))^2]}=\sqrt{AB^2+AC^2+2AB\times AC\cos \beta\cos \gamma} \]

实际上要将 \(-\cos \beta\cos \gamma\) 与一般情况的 \(\cos \angle BAC\) 进行比较

这种情况考虑完了，我们再来考虑一般的情况，这时就能够手工弄一个二面角出来。

那么两条红边的长度分别为 \(h\tan \alpha\) 与 \(h\tan (\beta-\alpha)\)，绿边的长度用余弦定理就是 \(\large \sqrt{(h\tan \alpha)^2+(h\tan (\beta-\alpha))^2-2h\tan \alpha\times h\tan (\beta-\alpha)\cos\gamma}\)

又因为两条蓝边的长度分别为 \(\frac{h}{\cos\alpha}\) 与 \(\frac{h}{\cos(\beta-\alpha)}\)，所以用余弦定理就可以知道

\[\large \cos \angle BAC=\frac{(\frac{h}{\cos\alpha})^2+(\frac{h}{\cos(\beta-\alpha)})^2-[(h\tan \alpha)^2+(h\tan (\beta-\alpha))^2-2h\tan \alpha\times h\tan (\beta-\alpha)\cos\gamma]}{2\frac{h}{\cos\alpha}\times \frac{h}{\cos(\beta-\alpha)}} \]

又因为 \(\frac{1}{\cos^2\alpha}-\tan^2\alpha=1\)，所以

\[\large \cos \angle BAC=\cos\alpha\cos(\beta-\alpha)+\sin\alpha\sin(\beta-\alpha)\cos\gamma \]

这个式子有点难观察其性质，不妨用积化和差展开，也就是

\[\cos\alpha\cos(\beta-\alpha)=\frac{1}{2}[\cos(\beta-2\alpha)+\cos\beta] \]

\[\sin\alpha\sin(\beta-\alpha)=\frac{1}{2}[\cos(\beta-2\alpha)-\cos\beta] \]

那么

\[\cos \angle BAC=\frac{1}{2}[(1-cos\gamma)\cos\beta+(1+\cos\gamma)\cos(\beta-2\alpha)] \]

前面是定值，后面的 \(1+\cos\gamma\) 恒为正数，所以当 \(\beta-2\alpha=0\) 时取得最大值

不妨此刻与 \(-\cos \beta\cos \gamma\) 进行比较，也就是需要证明

\[\frac{1}{2}[(1-\cos\gamma)\cos\beta+1+\cos\gamma]>-\cos\beta\cos\gamma \]

移项可以发现 \((1+\cos\gamma)(1+\cos\beta)\) 恒大于零，所以直角的情况不是最优解。

综上，当 \(AD\) 为 \(\angle BAC\) 的角平分线时，折叠后的 \(BC\) 取得最大值。

---

后续

本文起草于2023.3.29，在今天也就是2023.4.26写完，鸽了一个月真有我的。
其实证明结论的时间更早，当时觉得很想写篇博客纪念一下，没想到搁置到现在才写完。
证明其实除了积化和差就没有什么难的地方了，但是字母很多，要检查挺久的。
而且第二个版本在这里的做法还是优化过的，就很爽，毕竟之前版本的基本不等式太难写了。
Ending