仙人掌图小记

前言

本文仅介绍仙人掌图定义和性质，不涉及圆方树等内容

---

HDU 3594 Cactus

题目

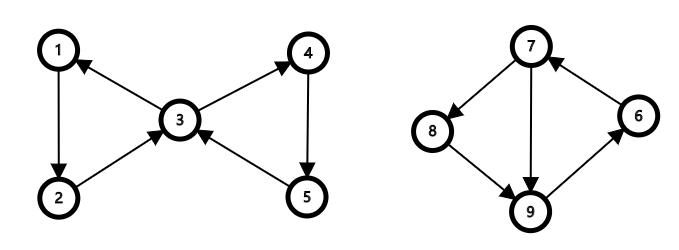
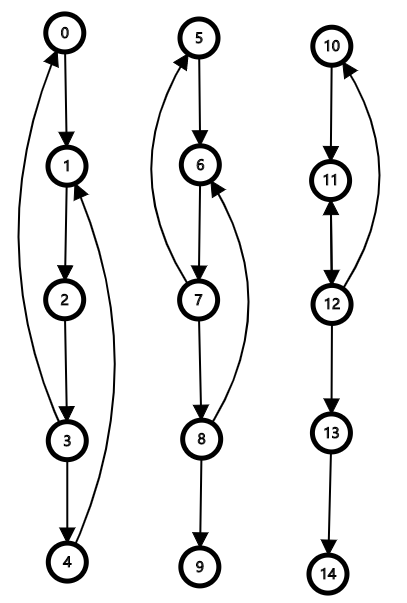
要做对这道题首先要读懂题目，可以看一下下面两张图：

定义（边仙人掌）：

1. 强连通图
2. 每条边至多属于一个简单环中

特别地，点仙人掌需要满足每个点至多属于一个简单环中，

那么，所有的点仙人掌都是边仙人掌。

本题的题意即为判断一个有向图是否为边仙人掌。

上图中左图为边仙人掌（不是点仙人掌），右图不是仙人掌。

一开始认为左图不是仙人掌图的可以看一下简单环的定义：

定义（简单环）：

除了环的首尾外，剩下的部分不会经过重复的点的环，

所以左图所谓的(1->2->3->4->5->3->1)并不是简单环，

根据简单环的定义，那么一个有向图是点仙人掌当且仅当它为至多存在一个简单环的强连通图，

至多是因为孤立点不存在简单环，对于一般情况，就是一个简单环。

不够严谨的证明：

如果两个简单环拼接在一起，

那么必然存在一个点在两个简单环上，

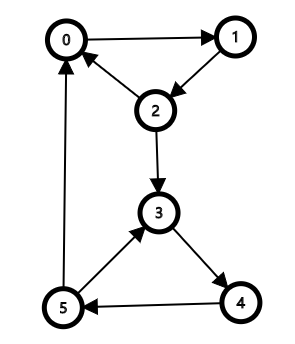
不然这个图不是强连通图，如下图就连边仙人掌都不是；

这张图仅仅是边仙人掌，但是它并不是点仙人掌。

---

前置知识

有向图应该要比无向图难判定。

考虑仙人掌图的三条性质（需要结合有向图的Tarjan算法）：

如果满足这三条性质那么这个图就是仙人掌图（不会证明必要性）。

时间戳: \(dfn[x]\) ，追溯值： \(low[x]\) 。

流图中每条有向边 \((x,y)\) 必然是以下四种之一：

1. 树枝边， 搜索树上的边， \(x\) 是 \(y\) 的父节点，即 \(fa[y][0]=x\) 。

2. 前向边， 在搜索树中 \(x\) 是 \(y\) 的祖先节点，即 \(fa[y][i]=x\) 。

3. 后向边， 在搜索树中 \(y\) 是 \(x\) 的祖先节点，即 \(fa[x][i]=y\) 。

4. 横叉边， 不存在祖先关系，一定满足 \(dfn[y]<dfn[x]\) 。

---

性质

1.仙人掌图的搜索树只存在树枝边和后向边

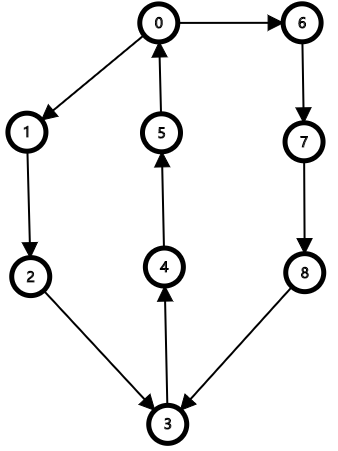
如果存在横叉边或是前向边，那么就会存在一条边在至少两个简单环上，否则

如上图，(8->3)是一条横叉边，但明显（3->0）路径上的边都经过两个简单环

2. 若 \(x\) 是 \(y\) 的父节点，则 \(dfn[x]\geq low[y]\)

如果 \(dfn[x]<low[y]\) 那么以\(y\)为根的子搜索树没有点能够回到流图的源点

那么 \((x->y)\) 就是一个桥，这个图不是强连通图

3. 如果有个点 \(x\) 有 \(g\) 个儿子的追溯值小于 \(dfn[x]\) ,同时点 \(x\) 有 \(h\) 条后向边，那么 \(g+h<2\)

分类讨论，左图为 \(g=0,h=2\) ，中图为 \(g=h=1\) ，右图为 \(g=2,h=0\) ，它们都存在一条边在至少两个简单环上

综上所述，仙人掌图的三条性质为：

1. 仙人掌图的搜索树只存在树枝边和后向边

2. 若 \(x\) 是 \(y\) 的父节点，则 \(dfn[x]\geq low[y]\)

3. 如果有个点 \(x\) 有 \(g\) 个儿子的追溯值小于 \(dfn[x]\) ,同时点 \(x\) 有 \(h\) 条后向边，那么 \(g+h<2\)

---

分析

知道这三条性质，就尝试怎样判定一个有向图是否为边仙人掌

首先，它是强连通图，所以只有一个强连通分量

其次，一定满足\(dfn[x]\geq low[y]\)

最后就是要满足第三条性质

不知道为什么第一条性质没有判断都可以过，

若有什么不对劲的地方，求HACK

---

代码

#include <cstdio>
#include <cctype>
#include <stack>
#include <cstring>
#define rr register
using namespace std;
const int N=20011; stack<int>stac;
struct node{int y,next;}e[N*3]; bool v[N];
int dfn[N],low[N],TOT,cnt,n,k,tot,flag,as[N];
inline signed iut(){
	rr int ans=0; rr char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
inline signed min(int a,int b){return a<b?a:b;}
inline void tarjan(int x){
	dfn[x]=low[x]=++tot;
	stac.push(x); v[x]=1;
	rr int TOT=0;
	for (rr int i=as[x];i;i=e[i].next)
	if (!dfn[e[i].y]){
		tarjan(e[i].y);
		low[x]=min(low[x],low[e[i].y]);
		if (low[e[i].y]<dfn[x]) ++TOT;
		if (low[e[i].y]>dfn[x]) flag=0;//第二条性质
	}
	else if (v[e[i].y])
	    low[x]=min(low[x],dfn[e[i].y]),++TOT;
	if (TOT>1) flag=0;//第三条性质
	if (dfn[x]==low[x]){
		++cnt; rr int y;
		do{
			y=stac.top();
			stac.pop();
			v[y]=0;
		}while (x!=y);
	}
}
signed main(){
	for (rr int T=iut();T;--T){
		n=iut(),k=flag=1,cnt=TOT=tot=0;
		memset(dfn,0,sizeof(dfn));
		memset(low,0,sizeof(low));
		memset(as,0,sizeof(as));
		for (rr int m=iut();m;--m){
			rr int x=iut()+1,y=iut()+1;
			e[++k]=(node){y,as[x]},as[x]=k;
		}
		for (rr int i=1;i<=n;++i)
		    if (!dfn[i]) tarjan(i);
		if (cnt>1||!flag) printf("NO\n");//有一条不满足即为NO
		    else printf("YES\n");
	}
	return 0;
}