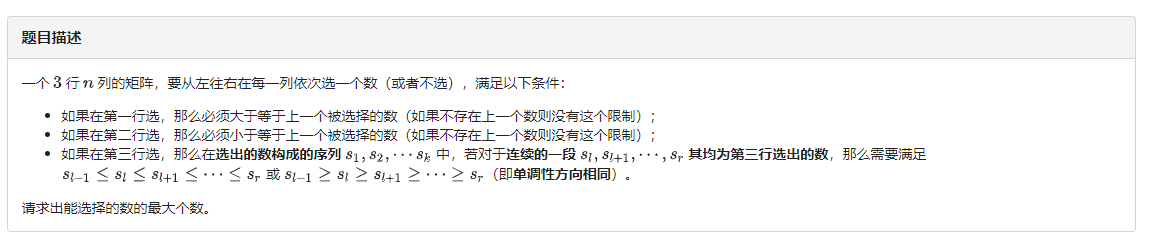
#树状数组，离散#C 波动序列

---

分析

设\(dp[i][j][0/1/2/3]\)表示前\(i\)个位置当前选的数为\(j\)，
且选择的是第一行/第二行/第三行不下降/第三行不上升，
状态转移方程显然，用线段树或者树状数组维护一下就可以了

---

代码

#include <cstdio>
#include <cctype>
#include <algorithm>
#define rr register
using namespace std;
const int N = 100011;
int n, m, a[3][N], b[N * 3];
inline signed iut() {
    rr int ans = 0, f = 1;
    rr char c = getchar();
    while (!isdigit(c)) f = (c == '-') ? -f : f, c = getchar();
    while (isdigit(c)) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
    return ans * f;
}
inline signed max(int a, int b) { return a > b ? a : b; }
inline signed fan(int now) { return m - now + 1; }
struct Tree_Array {
    int c[N * 3];
    inline void update(int x, int y) {
        for (; x <= m; x += -x & x) c[x] = max(c[x], y);
    }
    inline signed query(int x) {
        rr int ans = 0;
        for (; x; x -= -x & x) ans = max(ans, c[x]);
        return ans;
    }
} h[3][2];
signed main() {
    freopen("sequence.in", "r", stdin);
    freopen("sequence.out", "w", stdout);
    n = iut();
    for (rr int i = 1; i <= n; ++i) a[0][i] = iut(), b[++m] = a[0][i];
    for (rr int i = 1; i <= n; ++i) a[1][i] = iut(), b[++m] = a[1][i];
    for (rr int i = 1; i <= n; ++i) a[2][i] = iut(), b[++m] = a[2][i];
    sort(b + 1, b + 1 + m), m = unique(b + 1, b + 1 + m) - b - 1;
    for (rr int i = 1; i <= n; ++i)
        a[0][i] = lower_bound(b + 1, b + 1 + m, a[0][i]) - b,
        a[1][i] = lower_bound(b + 1, b + 1 + m, a[1][i]) - b,
        a[2][i] = lower_bound(b + 1, b + 1 + m, a[2][i]) - b;
    for (rr int i = 1; i <= n; ++i) {
        rr int f1 = max(h[0][0].query(a[0][i]), max(h[1][0].query(a[0][i]), h[2][0].query(a[0][i]))) + 1;
        rr int f2 =
            max(h[0][1].query(fan(a[1][i])), max(h[1][1].query(fan(a[1][i])), h[2][1].query(fan(a[1][i])))) +
            1;
        rr int f3 = max(h[0][0].query(a[2][i]), h[1][0].query(a[2][i])) + 1,//一直不下降
               f4 = max(h[0][1].query(fan(a[2][i])), h[2][1].query(fan(a[2][i]))) + 1;//一直不上升
        h[0][0].update(a[0][i], f1), h[0][1].update(fan(a[0][i]), f1), h[0][0].update(a[1][i], f2),
            h[0][1].update(fan(a[1][i]), f2), h[1][0].update(a[2][i], f3), h[1][1].update(fan(a[2][i]), f3),
            h[2][0].update(a[2][i], f4), h[2][1].update(fan(a[2][i]), f4);
    }
    return !printf("%d", max(h[0][0].query(m), max(h[1][0].query(m), h[2][0].query(m))));
}