【LGR-065】洛谷11月月赛 III Div.1
T1 基础博弈练习题
分析
首先区间长度为1的情况特判,偶数必胜,奇数必败
考虑倒推,如果最后一个位置为偶数那么该位置为必败局面,否则为必胜局面
因为先手到这个位置要减去1就会让后手为偶数就赢了
那么如果是偶数显然不能走这一格,奇数那么前\(m-1\)个位置都是必败局面
可以从该位置向第一个必胜局面连边(前驱),
如果\([l\sim r]\)中\(l\)必然会到\(r\)(不然后手可以通过其它方式必胜)
也就是\(r\)在\(l\)的子树内时才会必胜
那么可以用dfs序\(O(n)\)预处理
代码
#include <cstdio>
#include <cctype>
#include <cstring>
#define rr register
using namespace std;
const int N=1000011;
struct node{int y,next;}e[N];
int A,B,C,P,n,m,Q,typ,dfn[N],Fa[N],tot,k,as[N],rfn[N],a[N];
inline signed iut(){
rr int ans=0; rr char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
return ans;
}
inline void add(int x,int y){e[++k]=(node){y,as[x]},as[x]=k;}
inline signed rnd(){return A=(A*B+C)%P;}
inline void dfs(int x){
dfn[x]=++tot;
for (rr int i=as[x];~i;i=e[i].next)
dfs(e[i].y);
rfn[x]=tot;
}
signed main(){
memset(as,-1,sizeof(as));
n=iut(),m=iut(),Q=iut(),typ=iut();
for (rr int i=1;i<=n;++i) a[i]=iut();
if (typ) A=iut(),B=iut(),C=iut(),P=iut();
for (rr int i=1;i<=n;++i){
rr int Le=i>m?i-m-1:0;
if (a[i]&1){
if (a[Le]&1) Fa[i]=Le,add(Le,i);//两个位置都是奇数必胜
else Fa[i]=Fa[Le],add(Fa[Le],i);//找到这个点的前驱
}else{
if (a[i-1]&1) Fa[i]=i-1,add(i-1,i);//直接连上一个位置
else Fa[i]=Fa[i-1],add(Fa[i-1],i);//同理
}
}
dfs(0);
rr unsigned sum=0,ans=0;
for (rr int i=1,l,r;i<=Q;++i){
sum+=i+i-1;
if (typ){
l=rnd()%n+1,r=rnd()%n+1;
if (l>r) l^=r,r^=l,l^=r;
}else l=iut(),r=iut();
if (l==r) ans+=a[l]&1?0:sum;
else if (dfn[l]>dfn[r]||dfn[r]>rfn[l])
ans+=sum;
}
return !printf("%u",ans);
}
T2 基础最优化练习题
分析
贪心,对于\(w\)是负数,肯定要选择减\(k\),因为减\(k\)不会影响以后的限制
如果是正数,还要考虑限制,首先先加上\(k\),然后如果超过限制往当前\(a_i\)移动,
首先最多可以减\(2k\),然后我肯定要选\(w\)最小的位置,那可以用堆处理,
找出\(w\)最小的位置,提取它能减小的次数,把答案减小,如果次数还有重新放回堆里,时间复杂度\(O(nlogn)\)
代码
#include <cstdio>
#include <cctype>
#include <algorithm>
#define rr register
using namespace std;
typedef long long lll;
const int N=1000011;
struct rec{
lll w; int c;
bool operator <(const rec &t)const{
return w<t.w;
}
}heap[N];
int a[N],n,k,now,cnt; lll w[N],ans;
inline signed iut(){
rr int ans=0,f=1; rr char c=getchar();
while (!isdigit(c)) f=(c=='-')?-f:f,c=getchar();
while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
return ans*f;
}
inline void Push(rec w){
heap[++cnt]=w;
rr int x=cnt;
while (x>1){
if (heap[x]<heap[x>>1])
swap(heap[x>>1],heap[x]),x>>=1;
else return;
}
}
inline void Pop(){
heap[1]=heap[cnt--];
rr int x=1;
while ((x<<1)<=cnt){
rr int y=x<<1;
if (y<cnt&&heap[y+1]<heap[y]) ++y;
if (heap[y]<heap[x]) swap(heap[y],heap[x]),x=y;
else return;
}
}
signed main(){
n=iut(),k=iut();
for (rr int i=1;i<=n;++i) a[i]=iut();
for (rr int i=1;i<=n;++i) w[i]=iut();
for (rr int i=n-1;i;--i) w[i]+=w[i+1];
for (rr int i=1;i<=n;++i){
if (w[i]>0) ans+=w[i]*k,now+=k,Push((rec){w[i],k<<1});
else ans-=w[i]*k,now-=k;
while (now>a[i]){
rr rec t=heap[1]; Pop();
rr int less=min(now-a[i],t.c);
ans-=less*t.w,now-=less;
if (less<t.c) Push((rec){t.w,t.c-less});
}
}
return !printf("%lld",ans);
}
T3 基础函数练习题
分析
如果学过笛卡尔树就知道要建一棵笛卡尔树(\(O(n)\)单调栈)
等于说两头往它们的LCA跳,分别处理,以左端点为例
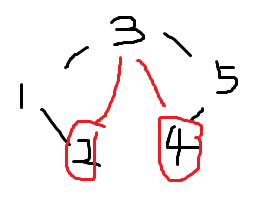
如果处理2~4,红色边才是应该找的,假设搜索到点\(x\)
这需要对之前的倍增数组有修改,比如说准备访问右端点时,父亲应该定为该点的父亲。
需要预处理\(x\)到\(f[x][i]\)的\(w\)总和(常规操作)和
\(f[x][i]\)的子树\(w\)总和(不包括\(x\)的左子树,右端点为右子树)(避免算重)
然后倍增的道理就是拼凑结果,也没有什么好说的了
可惜O2MLE了(常数小内存大直接暴毙)
代码
#include <cstdio>
#include <cctype>
#include <cmath>
#include <cstring>
#define rr register
using namespace std;
typedef long long lll;
const int N=500011;
lll s[N],ans[N],lin[N][19],sub[N][19];
int root,Lc[N],Rc[N],bas,w[N],f[N][19];
int a[N],n,Q,dep[N],B,l[N],r[N],LCA[N],st[N];
inline signed iut(){
rr int ans=0,f=1; rr char c=getchar();
while (!isdigit(c)) f=(c=='-')?-f:f,c=getchar();
while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
return ans*f;
}
inline void print(lll ans){
if (ans>9) print(ans/10);
putchar(ans%10+48);
}
inline lll max(lll a,lll b){return a>b?a:b;}
inline signed DiKaEr(){
rr int top=0; a[0]=2e9;
for (rr int i=1;i<=n;++i) a[i]=iut();
for (rr int i=1,lst=0;i<=n;++i){
while (a[st[top]]<a[i]) --top;
if (top<lst) Lc[i]=st[top+1];
if (top) Rc[st[top]]=i;
st[lst=++top]=i;
}
for (rr int i=0;i<=n;++i) a[i]=0;
for (rr int i=1;i<=n;++i) a[Lc[i]]=a[Rc[i]]=1;
for (rr int i=1;i<=n;++i) if (!a[i]) return i;
return 0;
}
inline void dfs1(int x,int fa){
dep[x]=dep[fa]+1,f[x][0]=fa;
for (rr int i=0;i<B&&f[x][i];++i)
f[x][i+1]=f[f[x][i]][i];
if (Lc[x]) dfs1(Lc[x],x);
if (Rc[x]) dfs1(Rc[x],x);
s[x]=max(s[Lc[x]],s[Rc[x]])+w[x];
}
inline signed lca(int x,int y){
if (dep[x]<dep[y]) x^=y,y^=x,x^=y;
for (rr int i=B;~i;--i)
if (dep[f[x][i]]>=dep[y]) x=f[x][i];
if (x==y) return x;
for (rr int i=B;~i;--i)
if (f[x][i]!=f[y][i])
x=f[x][i],y=f[y][i];
return f[x][0];
}
inline void dfs2(int x,bool z){
lin[x][0]=w[x],sub[x][0]=w[x]+(z?s[Lc[x]]:s[Rc[x]]);
for (rr int i=0;i<B&&f[x][i];++i){
f[x][i+1]=f[f[x][i]][i],lin[x][i+1]=lin[x][i]+lin[f[x][i]][i],
sub[x][i+1]=max(lin[f[x][i]][i]+sub[x][i],sub[f[x][i]][i]);
}
if (Lc[x]) f[Lc[x]][0]=z?f[x][0]:x,dfs2(Lc[x],z);
if (Rc[x]) f[Rc[x]][0]=z?x:f[x][0],dfs2(Rc[x],z);
}
inline lll query(int x,int y){
rr lll ans=0;
for (rr int i=B;~i;--i)
if (dep[f[x][i]]>=dep[y]){
ans=max(ans+lin[x][i],sub[x][i]);
x=f[x][i];
}
return ans;
}
signed main(){
n=iut(),Q=iut(),root=DiKaEr(); for (B=0;(2<<B)<=n;++B);
for (rr int i=1;i<=n;++i) w[i]=iut(); dfs1(root,0);
for (rr int i=1;i<=Q;++i) l[i]=iut(),r[i]=iut();
for (rr int i=1;i<=Q;++i) LCA[i]=lca(l[i],r[i]);
for (rr int i=1;i<=Q;++i) ans[i]=-1e16;
memset(f,0,sizeof(f)),dfs2(root,0);
for (rr int i=1;i<=Q;++i) ans[i]=max(ans[i],query(l[i],LCA[i])+w[LCA[i]]);
memset(f,0,sizeof(f)),dfs2(root,1);
for (rr int i=1;i<=Q;++i) ans[i]=max(ans[i],query(r[i],LCA[i])+w[LCA[i]]);
for (rr int i=1;i<=Q;++i){
if (ans[i]<0) putchar('-'),ans[i]=-ans[i];
print(ans[i]),putchar(10);
}
return 0;
}
T4 基础数论函数题
分析
求区间LCM对\(10^9+7\)取模,多组数据多组询问,
\(n,T,Q\leq 300,a\leq 2^{60}\)
分析
首先\(2^{60}\)不能接受,因为除法和取模存在冲突,这就要求没有除法
那可以将LCM转换为区间积,也就是用当前数剔除之前存在的GCD,
那么就可以获得\(O(Tqn^2)\)的代码,把在线换成离线分治,时间复杂度是\(O(Tn^2)\)
回过头看一下怎样剔除GCD,可以用取模的方式实现
至于为什么没有\(GCD\)的常数,给出一部分代码就知道了
for (int j=mid+1;j<=r;++j) c[j]=mul(c[j-1],b[j],b[i]);//在后半部分剔除b[i]的约数
lll GCD=gcd(c[r],b[i]);//gcd(b[i],b[mid+1]*b[mid+2]*...*b[r-1]*b[r])
for (int j=r-1;j>=mid;--j)
if (c[j]%GCD){//gcd(b[j+1],GCD)必然不等于1
lll Gcd=gcd(c[j],GCD);
b[j+1]=b[j+1]/(GCD/Gcd),GCD=Gcd;//消约数
}
显然只有log个位置会被算上
代码
#include <cstdio>
#include <cctype>
#define rr register
using namespace std;
typedef long long lll;
const lll mod=1000000007;
lll a[301],b[301],c[301];
int ans[301][301],n,Q;
inline lll iut(){
rr lll ans=0; rr char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
return ans;
}
inline lll gcd(lll a,lll b){return b?gcd(b,a%b):a;}
inline lll mul(lll a,lll b,lll mod){
a=a%mod,b=b%mod;
rr lll t=(long double)a*b/mod,ans=a*b-t*mod;
ans=ans<0?ans+mod:ans,ans=ans>=mod?ans-mod:ans;
return ans;
}
inline void print(int ans){
if (ans>9) print(ans/10);
putchar(ans%10+48);
}
inline void divi(int l,int r){
if (l==r){
ans[l][r]=a[l]%mod;
return;
}
rr int mid=(l+r)>>1;
divi(l,mid),divi(mid+1,r);
rr lll t,t1=1,t2=1;
for (rr int i=mid;i>=l;--i){
b[i]=a[i],t=1;
for (rr int j=i+1;j<=mid;++j)
t=mul(t,b[j],b[i]);
b[i]=b[i]/gcd(b[i],t);
}
for (rr int i=mid+1;i<=r;++i){
b[i]=a[i],t=1;
for (rr int j=i-1;j>mid;--j)
t=mul(t,b[j],b[i]);
b[i]=b[i]/gcd(b[i],t);
}
for (rr int i=mid;i>=l;--i){
t2=t1=b[i]%mod*t1%mod,c[mid]=1;
for (rr int j=mid+1;j<=r;++j)
c[j]=mul(c[j-1],b[j],b[i]);
rr lll GCD=gcd(c[r],b[i]);
for (rr int j=r-1;j>=mid;--j)
if (c[j]%GCD){
rr lll Gcd=gcd(c[j],GCD);
b[j+1]=b[j+1]/(GCD/Gcd),GCD=Gcd;
}
for (rr int j=mid+1;j<=r;++j)
t2=ans[i][j]=b[j]%mod*t2%mod;
}
}
signed main(){
for (rr int Test=iut();Test;--Test){
n=iut(),Q=iut();
for (rr int i=1;i<=n;++i) a[i]=iut();
divi(1,n);
for (rr int l,r;Q;--Q,putchar(10))
l=iut(),r=iut(),print(ans[l][r]);
}
return 0;
}

