#动态规划,组合计数,树状数组,前缀和#F 简单计数题&K 最简单的题
先膜两位出题人
F 简单计数题
题目
有\(n\)个活动,预约期有\(k\)天,第\(j\)天YC可以获得\(a_j(1\leq a_j\leq n)\)张预约券,
他会在\(n\)个活动中等概率选择\(a_k\)个活动消耗预约券,
\(k\)天后,YC同时参加\(n\)个活动的信心就提高了\(\prod_{i=1}^nw_i\),\(w_i\)表示第\(i\)个活动消耗的预约券个数
问他能同时参加\(n\)个活动的信心的期望是多少,为了方便统计,答案乘上\(\prod_{i=1}^nC(n,a_i)\)并对\(10^9+7\)取模
分析
首先乘上最后那一坨就是将期望转换成了贡献和,因为那一坨就是方案数。
接着,贡献就是从\(w_{1\sim n}\)中各抽取1个的方案(乘法原理)
考虑拎出\(n\)个出来,如果有一种方案第\(j\)天的预约券中选择了\(p_j\)张,且\(n=\sum_{i=1}^kp_i\)
那么这种方案的贡献就是\(\prod_{i=1}^kC(n-p_i,a_i-p_i)\),
因为已经保证抽出来了,那么剩下的预约券可以随便分配
那么就可以列\(dp\)方程,设\(dp[i][j]\)表示前\(i\)天预约券共拎出\(j\)张的贡献,那么
其中\(dp[0][0]=1\)
代码
#include <cstdio>
#include <cctype>
#define rr register
using namespace std;
const int mod=1000000007,N=1011;
int dp[21][N],c[N][N],n,k,a[N];
inline signed iut(){
rr int ans=0; rr char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
return ans;
}
inline signed mo(int x,int y){return x+y>=mod?x+y-mod:x+y;}
signed main(){
n=iut(),k=iut(),c[0][0]=dp[0][0]=1;
for (rr int i=1;i<=n;++i){
c[i][0]=c[i][i]=1;
for (rr int j=1;j<i;++j)
c[i][j]=mo(c[i-1][j-1],c[i-1][j]);
}
for (rr int i=1;i<=k;++i) a[i]=iut();
for (rr int i=1;i<=k;++i)
for (rr int j=0;j<=n;++j) if (dp[i-1][j])
for (rr int p=0;p<=n;++p){
if (j+p>n||p>a[i]) break;
rr int t=1ll*c[j+p][p]*c[n-p][a[i]-p]%mod;
dp[i][j+p]=mo(dp[i][j+p],1ll*t*dp[i-1][j]%mod);
}
return !printf("%d",dp[k][n]);
}
K 最简单的题
题目
给出两个长度为\(n\)的数列\(a,b\),
设\(f(i,j)=LIS(a_i,b_i,a_j,b_j)\),
问\(f(i,j)=1\sim 4\)的个数
\(1\leq n\leq 10^5,1\leq a,b\leq m\leq 10^3\)
分析
枚举\(j\),然后分类讨论,标绿为所在位置
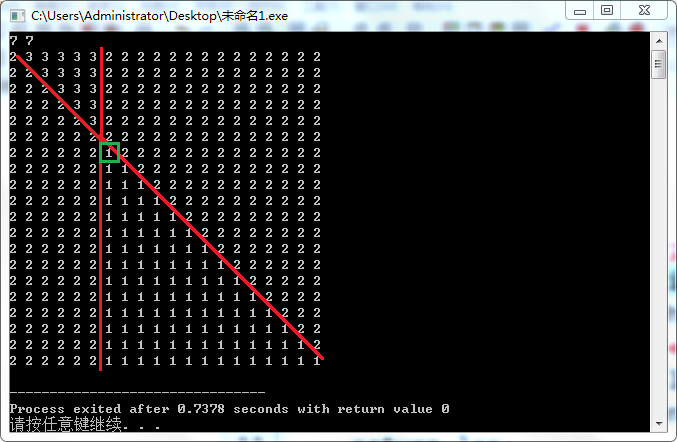
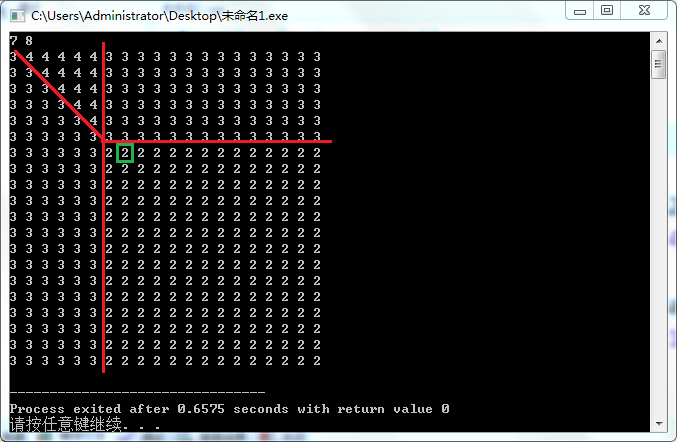
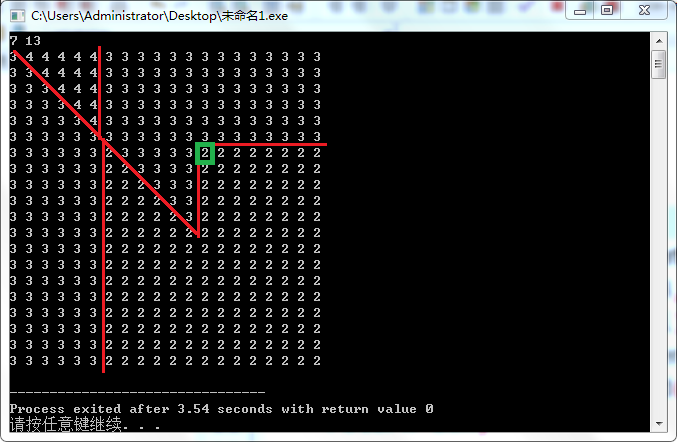
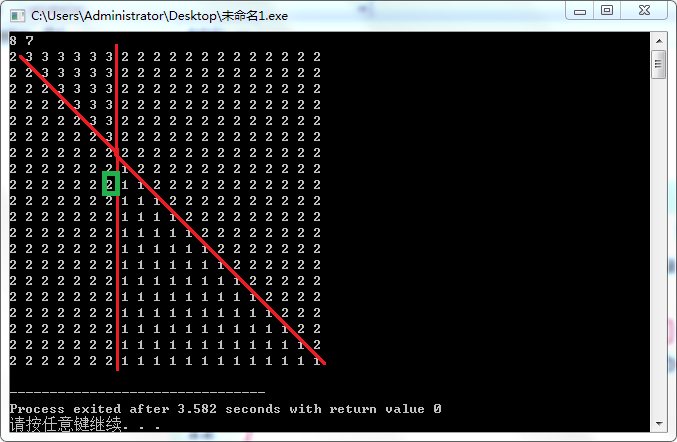
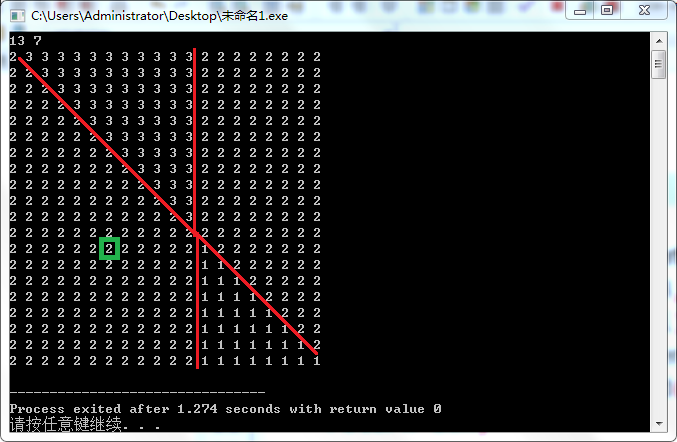
首先一共5种情况,考虑它们的共同规律,当\(a_j<b_j\)时,右边罕见的出现平的分界线
其它情况都是要将纵轴顺时针旋转45度,实际上是逆时针。
被BPM大爷嘲讽后恶补高中数学,学完后却发现我在想桃子
还不如直接说原\((x,y)\)对应\((x-y,y)\),当然要平移横坐标,加上\(m\)
如下图\(m=15\)的情况
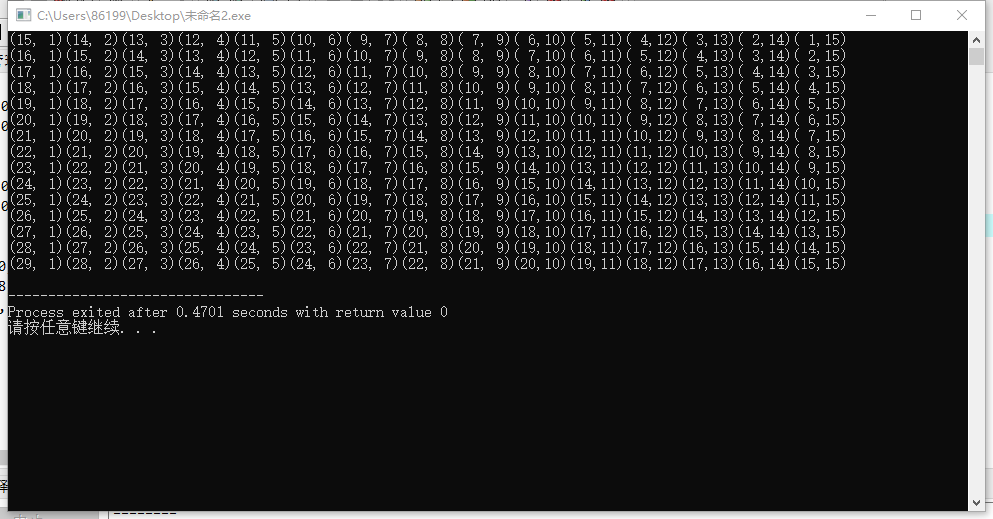
讲到这里好像还真是一道简单题
一开始我想的是用树状数组维护,但是BPM连\(STL::sort\)也没放过,
多组数据直接TLE(幸好O2卡过去了)
然后BPM就让我用前缀和做,其实思路差不多,
这里也不细讲了,反正代码很清晰
树状数组代码
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#define rr register
using namespace std;
const int N=100011;
int n,m,Cnt,c[N]; long long dp[5];
struct rec{int x,y;}a[N],b[N<<1];
inline signed iut(){
rr int ans=0; rr char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
return ans;
}
bool cmp1(rec a,rec b){return a.y>b.y;}
inline signed query(int x){rr int ans=0; for (;x;x-=-x&x) ans+=c[x]; return ans;}
inline void update(int x,int y){for (;x<=m;x+=-x&x) c[x]+=y;}
signed main(){
while (scanf("%d%d",&n,&m)==2){
dp[1]=dp[2]=dp[3]=dp[4]=0;
for (rr int i=1;i<=n;++i) a[i]=(rec){iut(),iut()};
for (rr int i=1;i<=n;++i) if (a[i].x<a[i].y)
b[++Cnt]=(rec){a[i].x,a[i].y-(a[i].x+1==a[i].y)};
sort(b+1,b+1+Cnt,cmp1),sort(a+1,a+1+n,cmp1);
for (rr int i=1,j=1;i<=Cnt;++i){
while (j<=n&&a[j].y>=b[i].y) update(a[j].x,1),++j;
rr int t=query(b[i].x-1); dp[3]+=t,dp[2]+=j-t-1;
}
Cnt=0,memset(c,0,sizeof(c));
for (rr int i=1;i<=n;++i) b[i]=(rec){a[i].x>=a[i].y,a[i].x}; Cnt=n;
for (rr int i=1;i<=n;++i) if (a[i].x<a[i].y) b[++Cnt]=(rec){2,a[i].y-(a[i].x+1==a[i].y)};
sort(b+1,b+1+Cnt,cmp1); for (rr int i=1;i<=n;++i) a[i].x-=a[i].y-m;
for (rr int i=1,j=1,t=0;i<=Cnt;++i){
while (j<=n&&a[j].y>=b[i].y) t+=a[j].x<m,++j;
rr int t2=(b[i].x==2)?-1:1,t1=b[i].x!=1;
dp[2+t1]+=t*t2,dp[1+t1]+=(j-t-1)*t2;
}
reverse(a+1,a+1+n),Cnt=0,memset(c,0,sizeof(c));
for (rr int i=1;i<=n;++i) b[i].y=a[i].x-m+a[i].y;
for (rr int i=1;i<=n;++i) b[i].x=a[i].x<m;
sort(b+1,b+1+n,cmp1),reverse(b+1,b+1+n);
for (rr int i=1,j=1,t=0;i<=n;++i){
while (j<=n&&a[j].y<b[i].y) t+=a[j].x<m,++j;
dp[3+b[i].x]+=t,dp[2+b[i].x]+=j-t-1;
}
printf("%lld %lld %lld %lld\n",dp[1],dp[2],dp[3],dp[4]);
memset(c,0,sizeof(c));
}
return 0;
}
前缀和代码
#include <cstdio>
#include <cctype>
#include <cstring>
#define rr register
using namespace std;
const int N=100011,M=1011;
int n,m,Cnt,K,s[M<<1][M],x[N],y[N];
inline signed iut(){
rr int ans=0; rr char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
return ans;
}
signed main(){
while (scanf("%d%d",&n,&m)==2){
rr long long dp[5]={0,0,0,0,0};
memset(s,0,sizeof(s)),K=m<<1;
for (rr int i=1;i<=n;++i)
x[i]=iut(),y[i]=iut(),++s[x[i]][y[i]];
for (rr int i=1;i<=m;++i)
for (rr int j=1;j<=m;++j)
s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
for (rr int i=1;i<=n;++i)
if (x[i]<y[i]){
rr int px=x[i],py=y[i]-(x[i]+1==y[i]);
dp[3]+=s[px-1][m]-s[px-1][py-1];
dp[2]+=s[m][m]-s[px-1][m]-s[m][py-1]+s[px-1][py-1];
}
for (rr int i=1;i<=m;++i)
for (rr int j=1;j<=m;++j) s[i][j]=0;
for (rr int i=1;i<=n;++i) x[i]-=y[i]-m,++s[x[i]][y[i]];
for (rr int i=1;i<=K;++i)
for (rr int j=1;j<=m;++j)
s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
for (rr int i=1;i<=n;++i){
rr int T=x[i]<m,F=x[i]+y[i]-m,G=y[i]-(F+1==y[i]);
rr int TEMP=s[K][m]-s[m-1][m]-s[K][F-1]+s[m-1][F-1];
dp[3+T]+=s[m-1][F-1],dp[1+T]+=TEMP;
dp[2+T]+=s[K][m]-TEMP-s[m-1][F-1];
if (!T) continue;
dp[2]-=s[K][m]-s[m-1][m]-s[K][G-1]+s[m-1][G-1];
dp[3]-=s[m-1][m]-s[m-1][G-1];
}
printf("%lld %lld %lld %lld\n",dp[1],dp[2],dp[3],dp[4]);
}
return 0;
}
吐槽和膜拜时间
两位出题人出的题都是码题难度不高,思维难度不低的题目
其中K题所花的改题时间更多了那么一两个月233
吐槽树状数组开了O2比前缀和不开O2还要慢
主要聊一聊K题,历程大概是这样的
两个月,什么也不会,干聊纯属浪费时间;
一个月,学习高中数学;一个月,改完K题
其中大概只有一个月时间是没有被浪费掉的
其实我一开始觉得题目超级难,主要是想起了不堪回首的记忆
但其实说难不难,BPM没有一味地去帮助我,而是让我自己去思考,
虽然有点不情愿,但是我觉得很有道理,
想起考完\(CSP-S\)之后\(WYC\)也给我提出了一些建议
好吧,不管怎么说一模加油,不要丢脸
upd:20200410

