#CDQ分治，单调栈，双指针#BZOJ 4237 稻草人 AT1225 かかし

洛谷传送门
BZOJ 4237 稻草人

---

题意

在一个平面直角坐标系上给出\(n\)个点，

问有多少个点对\((i,j)\)满足\(x_i<x_j,y_i<y_j\),

而且对于\(n\)个点中的任意一点都不在以点\(i\)为左下角，

点\(j\)为右上角的矩形内部（不包括边界）

---

分析

如果没有下面的限制应该是一道二维偏序裸题，但是限制不好搞

考虑用CDQ分治，也就是倘若\([l\sim mid]\)和\([mid+1\sim r]\)的答案已经弄好，处理区间不同的情况

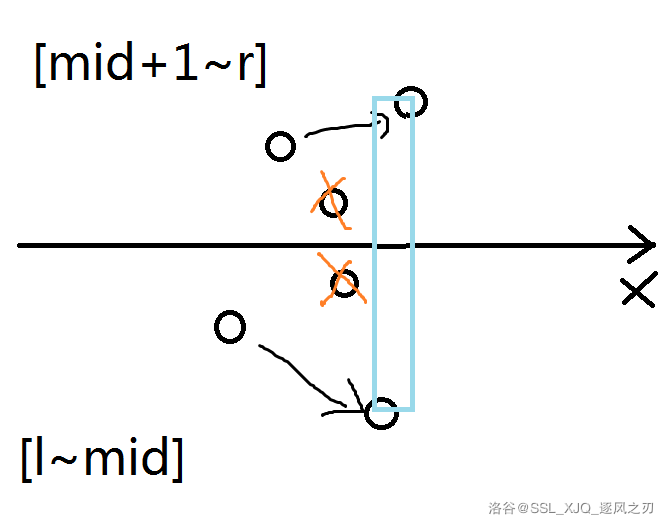
假设一开始以纵坐标升序排序，

处理完一个区间该区间就以横坐标升序排序，

那也就是能保证\([l\sim mid]\)的\(y\)，

均不超过\([mid+1\sim r]\)的\(y\)，

区间内部的\(x\)单调不降

枚举右上角的\(j\)，左下角可以用双指针，

那就可以确定一段左下角区间，因为区间内部\(x\)单调不降，

所以\([l\sim mid]\)的\(y\)单调不升才能不互相影响，

显然可以用单调栈维护；

那怎样判断右上角有没有影响，

只要查找到\(i\)左边第一个比它纵坐标小的点\(k\)就可以了，

显然还是可以用单调栈

然后左下角单调栈可选择的范围就是\(x_k\leq x_t\leq x_i\)

可以用二分来求，时间复杂度\(O(nlog^2n)\)

注意AT1225 かかし答案需要换行 （我就说我怎么WA了）

还是手画一张图好理解上面的抽象描述

---

代码

#include <cstdio>
#include <cctype>
#include <algorithm>
#define rr register
using namespace std;
const int N=200011;
int st2[N],st1[N],n;
long long ans;
struct rec{int x,y;}a[N],b[N];
inline signed iut(){
	rr int ans=0; rr char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
bool cmp(rec x,rec y){return x.y<y.y;}
inline signed divid(int l,int r,int z){//二分<z的最大值
	while (l<r){
		rr int mid=(l+r+1)>>1;
		if (a[st2[mid]].x<z) l=mid;
		    else r=mid-1;
	}
	return l;
}
inline void cdq(int l,int r){
	if (l==r) return;
	rr int mid=(l+r)>>1,T1=0,T2=0;
	cdq(l,mid),cdq(mid+1,r);
	for (rr int i=mid+1,j=l;i<=r;++i){
		while (T1&&a[i].y<a[st1[T1]].y) --T1;//右上角单调不降
		st1[++T1]=i;
		for (;a[j].x<a[i].x&&j<=mid;++j){
			while (T2&&a[j].y>a[st2[T2]].y) --T2;//左下角单调不升
			st2[++T2]=j;
		}
		if (a[st2[T2]].x>=a[st1[T1-1]].x)
			ans+=T2-divid(0,T2,a[st1[T1-1]].x);
	}
	rr int i1=l,j1=mid+1,T=0;
   //归并排序模板
	while (i1<=mid&&j1<=r)
	if (a[i1].x<=a[j1].x) b[++T]=a[i1],++i1;
	    else b[++T]=a[j1],++j1;
	while (i1<=mid) b[++T]=a[i1],++i1;
	while (j1<=r) b[++T]=a[j1],++j1;
	for (rr int i=1;i<=T;++i) a[l+i-1]=b[i];
}
signed main(){
	n=iut();
	for (rr int i=1;i<=n;++i)
	    a[i]=(rec){iut(),iut()};
	sort(a+1,a+1+n,cmp),cdq(1,n);
	return !printf("%lld\n",ans);
}