【题解】QOJ-7412 Counting Cactus
之前没做过仙人掌，甚至没学过圆方树，理解了半天改出来了，遂记。
尝试用理解树的方法理解一个仙人掌，钦定根为 \(u\)，那么一个与 \(u\) 有关的子仙人掌（类比子树）有如下两种情况：
-
一个 \(u\) 所在的环，环中除了 \(u\) 以外的节点挂任意仙人掌，套在根上。
-
一个 \(u\) 引出的边 \((u,v)\)，以 \(v\) 为根的一个仙人掌。
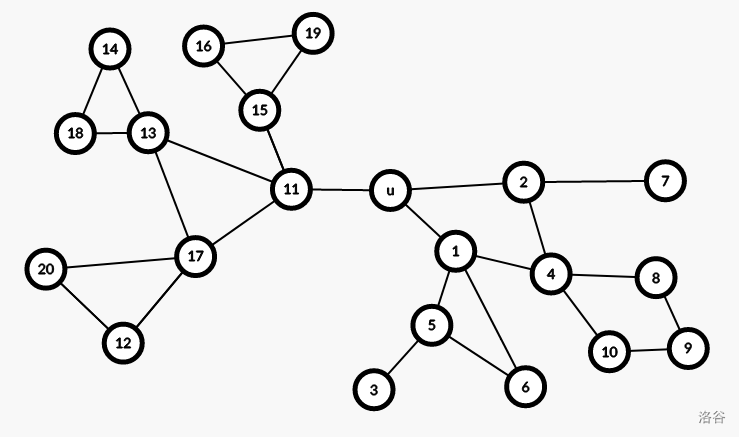
结合上图，\(1\sim 10\) 号节点构成的子仙人掌就是以环的形式套在根上，而另一个子仙人掌则是由 \(11\) 引出的，属于第二种情况。
最基本的状态设 \(f(S,u)\) 为点集 \(S\) 中以 \(u\) 为根的仙人掌个数。
根据上面对子仙人掌的讨论，我们知道第一种情况要求 \(u\) 的连边恰好有一个环，需要另设状态 \(g(S,u)\) 表示（具体定义同 \(f\)）；而第二种情况只要枚举连边再增加一个 \(f(T,v)\) 即可。
思考符合 \(g\) 定义的仙人掌怎么得到，可以理解成是一个链 \((v,w)\) 上挂若干仙人掌，存在边 \((u,v)\) 与 \((u,w)\)，形成一个环，注意到这里 \(u\) 在子图中只包含了两条边，是符合 \(g\) 要求的。
于是我们需要维护此类链的信息，定义为 \(h(S,u,v)\)。
在转移之前，规定单独一个点不属于 \(g\) 或 \(h\) 定义范畴内，但是属于 \(f\) 的。
转移 \(1\)：初始状态下链是由两个仙人掌拼起来的。
其中 \(T\subseteq S,u\in T,v\in S\setminus T,(u,v)\in E\)
转移 \(2\)：在链 \((v,w)\) 的一端增加一个点 \(u\)。
其中 \(T\subseteq S,u\in T,v,w\in S\setminus T,(u,v)\in E\)。
为了去重，钦定 \(v<w\)。
转移 \(3\)，将一个链用两条边并成一个符合 \(g\) 要求的环。
其中 \(u,v,w\in S,(u,v),(u,w)\in E\)。
转移 \(4\)，子仙人掌第一种情况，将环套在跟上。
其中 \(T\subseteq S,u\in T\)。
转移 \(5\)，子仙人掌第二情况，由一条链引出来。
其中 \(u\in T,v\in S\setminus T,(u,v)\in E\)。
要注意的是：在后两个转移中，加入一个子仙人掌会导致算重，因此我们钦定加入的子仙人掌为状态 \(S\setminus \{u\}\) 的 \(\operatorname{lowbit}\) 对应节点所在子仙人掌。
同时转移 \(3\) 的情况会在转移 \(4\) 中再传递给 \(f\)。（毕竟 \(g\) 是 \(f\) 的特殊情况。）
点击查看代码
int main(){
n=read(),m=read();
for(int i=1;i<=m;++i){
int u=read(),v=read();
E[u][v]=E[v][u]=1;
}
for(int i=1;i<=n;++i) f[(1<<i-1)][i]=1;
for(int s=1;s<(1<<n);++s){
for(int u=1;u<=n;++u){
if(!(s&(1<<u-1))) continue;
for(int v=1;v<=n;++v){
if(u==v) continue;
if(!(s&(1<<v-1))) continue;
if(!E[u][v]) continue;
for(int t=s^(1<<v-1);t;t=(t-1)&(s^(1<<v-1))){
if(!(t&(1<<u-1))) continue;
int t1=t,t2=s^t1;
h[s][u][v]=(h[s][u][v]+1ll*f[t1][u]*f[t2][v]%mod)%mod;
}
}
for(int v=1;v<=n;++v){
if(u==v) continue;
if(!(s&(1<<v-1))) continue;
if(!E[u][v]) continue;
for(int w=1;w<=n;++w){
if(u==w||v==w) continue;
if(!(s&(1<<w-1))) continue;
for(int t=s^(1<<v-1)^(1<<w-1);t;t=(t-1)&(s^(1<<v-1)^(1<<w-1))){
if(!(t&(1<<u-1))) continue;
int t1=t,t2=s^t1;
h[s][u][w]=(h[s][u][w]+1ll*f[t1][u]*h[t2][v][w]%mod)%mod;
}
}
}
for(int v=1;v<=n;++v){
if(u==v) continue;
if(!(s&(1<<v-1))) continue;
if(!E[u][v]) continue;
for(int w=v+1;w<=n;++w){
if(!(s&(1<<w-1))) continue;
if(!E[u][w]) continue;
g[s][u]=(g[s][u]+h[s^(1<<u-1)][v][w])%mod;
}
}
if(s!=(1<<u-1)){
int v=__lg(lowbit((s^(1<<u-1))))+1;
for(int t=s^(1<<v-1);t;t=(t-1)&(s^(1<<v-1))){
if(!(t&(1<<u-1))) continue;
int t1=t,t2=s^t1;
f[s][u]=(f[s][u]+1ll*f[t1][u]*g[t2|(1<<u-1)][u]%mod);
for(int w=1;w<=n;++w){
if(!(t2&(1<<w-1))) continue;
if(!E[u][w]) continue;
f[s][u]=(f[s][u]+1ll*f[t1][u]*f[t2][w]%mod)%mod;
}
}
}
}
}
printf("%d\n",f[(1<<n)-1][1]);
return 0;
}
