3.【考后总结】4 月清北营模拟赛 32023-04-24

4.24 冲刺清北营 5#

T1 吃粮#

先考虑静态。

树上随机游走，写出转移方程：

{\begin{cases} f_{u} = a_{u} & d e g_{u} = 1 \\ f_{u} = a_{u} + \frac{1}{d e g_{u}} \sum_{v \in s o n (u)} f_{v} + \frac{1}{d e g_{u}} f_{f a_{u}} & o t h e r w i s e \end{cases}

$\begin{cases} f_u=a_u&deg_u=1\\ f_u=a_u+\dfrac{1}{deg_{u}}\sum_{v\in \mathrm{son}(u)} f_v+\dfrac{1}{deg_u}f_{fa_u}&\mathrm{otherwise} \end{cases}$

这样只能 $O(n^3)$ 高斯消元，注意到只有 $f_{fa_{u}}$ 一个位置成环，套路性地考虑系数递推。

设 $f_u=k_u\times f_{fa_u}+b_u$ ，特别地，若 $u$ 为叶子 $k_u=0,b_u=a_u$ 。

把式子改一下：

d e g_{u} \times f_{u} = d e g_{u} \times a_{u} + \sum_{v \in s o n (u)} k_{v} \times f_{u} + b_{v} + f_{f a_{u}}

$deg_u\times f_u=deg_u\times a_u+\sum_{v\in \mathrm{son}(u)} k_v\times f_u+b_v+f_{fa_u}$

整理成：

f_{u} = \frac{1}{d e g_{u} - \sum_{v \in s o n (u)} k_{v}} f_{f a_{u}} + \frac{d e g_{u} \times a_{u} + \sum_{v \in s o n (u)} b_{v}}{d e g_{u} - \sum_{v \in s o n (u)} k_{v}}

$f_u=\dfrac{1}{deg_u-\sum_{v\in \mathrm{son}(u)}k_v}f_{fa_u}+\dfrac{deg_u\times a_u+\sum_{v\in \mathrm{son}(u)}b_v}{deg_u-\sum_{v\in \mathrm{son}(u)}k_v}$

于是有：

{\begin{cases} k_{u} = \frac{1}{d e g_{u} - \sum_{v \in s o n (u)} k_{v}} \\ b_{u} = \frac{d e g_{u} \times a_{u} + \sum_{v \in s o n (u)} b_{v}}{d e g_{u} - \sum_{v \in s o n (u)} k_{v}} \end{cases}

$\begin{cases} k_u=\dfrac{1}{deg_u-\sum_{v\in \mathrm{son}(u)}k_v}\\\\ b_u=\dfrac{deg_u\times a_u+\sum_{v\in \mathrm{son}(u)}b_v}{deg_u-\sum_{v\in \mathrm{son}(u)}k_v} \end{cases}$

这样到 $f_1$ 处时，因为此时没有 $f_{fa_1}$ 项，所以 $f_1=b_1$ 。

这样复杂度降到 $O(n)$ 。

考虑如何带修，因为每次只求 $b_1$ ，所以只考虑对 $b_1$ 的贡献，容易发现 $k_u$ 与 $a$ 无关，是常量。

对于修改一个非叶子节点 $u$ ，设修改变化量 $\Delta a$ ，对 $b_u$ 的影响为 $k_u\times deg_u\Delta a$ ，再套到 $b_{fa_u}$ 中，影响是 $k_{fa_u}\times k_u\times deg_u\Delta a$ ，因此对 $b_1$ 的影响就是根链上所有 $k$ 的累积乘 $deg_u\Delta a$ 。对于叶子节点，本身不再乘 $k$ 即可。

T2 平衡#

容易想到连边缩点。

之后是神秘做法。

一个点内的绝对值之和相当于是分段函数，构成了一个下凸包，很好维护。

易证明最终每个节点一定是出现过的 $w$ 值，因此排序后分治，考虑满足 $x\ge w_{mid}$ 的点集是什么。

接下来是更神秘结论：如果有 $x_i\le x_j$ 的限制，则向 $x_i\le x_j$ 连边，之后以 $w_{mid}$ 在每个点对应取值的导数为点权，跑最小权闭合子图，则子图内的节点可以在最优条件下满足 $x\ge w_{mid}$ ，其余则不能。

证明：如果存在最小权闭合子图的一个子图满足其中节点 $x_i<w_{mid}$ ，而我们由小向大连边，因此不满足条件的节点也是类似拓扑的点集，因此除去这个子图剩下的部分仍然是闭合子图，而剩下的子图的点权和不小于原图，因此删去部分的点权和非正。

点权和的实际意义是斜率，而 $x_i<w_{mid}$ 且下凸包斜率不降，所以对于每个节点， $w_{mid}$ 处的斜率一定不小于 $x_i$ 处斜率，而此时已知 $w_{mid}$ 处斜率之和非正，因此此时的结果一定不优于把 $x_i$ 改为 $w_{mid}$ 。

网络流求最小权闭合子图即可。

另外斜率定义为 $f(x)-f(x-1)$ ，因此在不可导处的斜率取左极限。

4.25 冲刺清北营 6#

T1 万家灯火#

以询问点为根，在连通块的最小深度位置记录答案，则是求有多少节点 $u$ 满足 $col_u=1$ 且 $col_{fa_u}=0$ 。

如果询问点唯一，那么考虑修改一个位置实际上产生了两部分的影响：对于自己和对于儿子。对于自己只需要判断父亲的情况，对于儿子则是要记录儿子中被点亮的个数，批量修改，有距离限制就需要树状数组维护一下。

放在无根树上，需要点分治，带修就用点分树。在每个分治中心统计以当前分治中心为根，子树内连通块个数，同样也是树状数组维护，套路地开两个分别维护对自己的贡献和对父亲的贡献，便于容斥。

有一个问题：如果我们修改了当前的分治中心的状态，会使得答案发生改变，同时也使得下一层对这一层的贡献发生改变，但我们不能暴力更改这些树状数组的信息。于是钦定一个分治子树的答案是基于分治中心被点亮计算的，这样统计答案时如果分治中心没有点亮，那么只需要把与分治中心连接的连通块拆成多个，就之和分治中心的儿子（除去上一层对应的）中被点亮个数有关，另外还需要特判当前统计到连通块和上一层统计到的实际是一个的情况。

T2 逃亡#

期望拆成每个位置被经过的概率之和，关键是考虑 $m=1$ 怎么做，剩下直接 $1-\prod(1-P_i)$ 求出至少被经过一次的概率就做完了。

默认到达位置在正方向，设 $p_i$ 为 $n$ 步恰好移动 $i$ 个单位的概率，容易得到前进了 $\dfrac{n+i}{2}$ 步，后退了 $\dfrac{n-i}{2}$ ，前提 $i$ 与 $n$ 在模 $2$ 意义下同余。

于是 $p_i=\dfrac{1}{2^n}\dbinom{n}{\tfrac{n+i}{2}}$ 。

接下来考虑经过 $i$ 概率 $P_i$ 。

考虑最终到达的位置 $j$ ，如果 $j>i$ ，则一定经过了 $i$ ，而 $j<i$ 的情况有一个很神仙的转化。

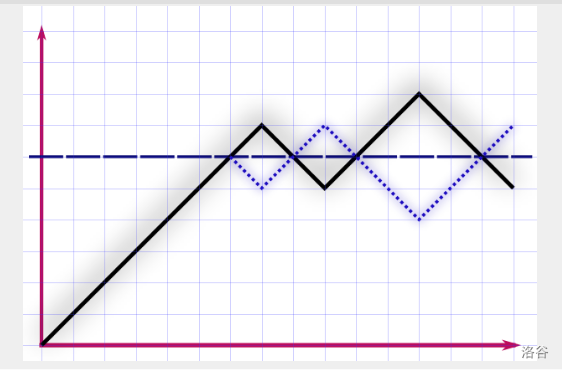
注意到实线部分是最终位置小于 $i$ 的，一定可以关于 $i$ 翻折得到最终位置大于 $i$ 的情况，因此二者本质相同，所以有：

P_{i} = 2 \sum_{j > i} p_{j} + p_{i}

$P_i=2\sum_{j>i} p_j+p_i$

之后 $O(nm)$ 覆盖求就可以了。

作者：SoyTony

出处：https://www.cnblogs.com/SoyTony/p/Simulation_Problems_of_THUSC_and_PKUSC_in_April_3.html

版权：本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。

posted @ 2023-04-24 19:30 SoyTony 阅读(46) 评论(0) 编辑收藏举报

Loading

SoyTony

【考后总结】4 月清北营模拟赛 3

4.24 冲刺清北营 5#

T1 吃粮#

T2 平衡#

4.25 冲刺清北营 6#

T1 万家灯火#

T2 逃亡#

公告

一言

搜索

合集 (8)

随笔分类 (863)

阅读排行榜

评论排行榜

推荐排行榜